2023-2024学年第二学期甘肃省武威第十七中学教研联片八年级数学开学学情评估(含答案)
文档属性
| 名称 | 2023-2024学年第二学期甘肃省武威第十七中学教研联片八年级数学开学学情评估(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 421.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 18:40:51 | ||
图片预览




文档简介
2023-2024学年第二学期甘肃省武威第十七中学教研联片
八年级数学开学学情评估
一、选择题(共30分)
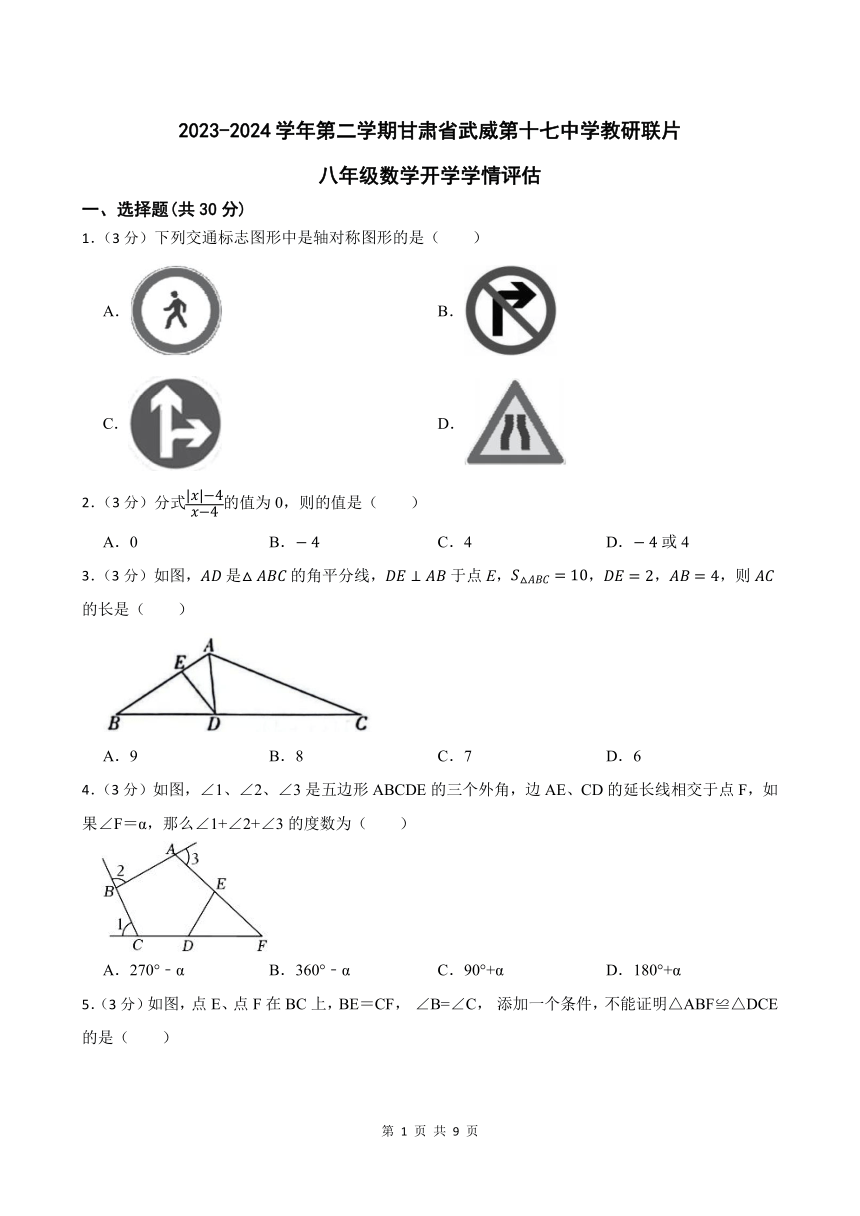
1.(3分)下列交通标志图形中是轴对称图形的是( )
A. B.
C. D.
2.(3分)分式的值为0,则的值是( )
A.0 B. C.4 D.或4
3.(3分)如图,是的角平分线,于点E,,,,则的长是( )
A.9 B.8 C.7 D.6
4.(3分)如图,∠1、∠2、∠3是五边形ABCDE的三个外角,边AE、CD的延长线相交于点F,如果∠F=α,那么∠1+∠2+∠3的度数为( )
A.270°﹣α B.360°﹣α C.90°+α D.180°+α
5.(3分)如图,点E、点F在BC上,BE=CF, ∠B=∠C, 添加一个条件,不能证明△ABF≌△DCE的是( )
A.∠A=∠D B.∠AFB=∠DEC
C.AB=DC D.AF=DE
6.(3分)如图,在中,,,的面积为12,于点,直线垂直平分交于点,交于点,是线段上的一个动点,分别连接,,则的周长的最小值是( )
A.6 B.7 C.10 D.12
7.(3分)若点,关于轴对称,则( )
A.; B.;
C.; D.;
8.(3分)下列运算正确的是( )
A. B.
C. D.
9.(3分)如图,任意画一个的,再分别作的两条角平分线和,和相交于点,连接,有以下结论:①;②平分;③;④;⑤,正确的有( )
A.5个 B.4个 C.3个 D.2个
10.(3分)甲车行驶千米与乙车行驶千米所用时间相同,已知乙车每小时比甲车多行驶千米,设甲车的速度为千米/小时,依题意列方程正确的是( )
A. B.
C. D.
二、填空题(共24分)
11.(3分)当x 时,分式 的值为零.
12.(3分)已知,,则 .
13.(3分)已知和关于x轴对称,则的值为 .
14.(3分)若多边形的每个内角都相等,它的一个外角等于36°,那么这个多边形的内角和等于 °.
15.(3分)如图,中边的垂直平分线分别交、于点、,,的周长为,则的周长是 .
16.(3分)如图,已知中,是边上的中线,为的中点,若的面积为,则的面积为 .
17.(3分)如图,已知△ABC≌△ADE,∠B=25°,∠E=98°,∠EAB=20°,则∠BAD的度数为 .
18.(3分)《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间,设规定时间为x天,则可列出正确的方程为 .
三、因式分解与解方程(共16分)
19.(8分)因式分解:
(1)(4分) (2)(4分)
20.(8分)解方程:
(1)(4分); (2)(4分).
四、解答题(共50分)
21.(6分) 等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,求这个等腰三角形的底边长.
22.(6分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
23.(6分)如图,点D为△ABC的边BC上一点,AC=AD=BD,∠BAD=34°,求∠CAB的度数.
24.(6分)如图,在中,于H,于F,交的延长线于E,且,.
(1)(3分)求证:平分;
(2)(3分)若,求的度数.
25.(8分)如图,在△ABD和△ACD中,AB=AC,BD=CD.
(1)(4分)求证:△ABD≌△ACD;
(2)(4分)过点D作DE∥AC交AB于点E,求证:AE=DE.
26.(8分)如图,在△ABC中,AB=AC, BC=6,AM平分∠BAC,D为AC的中点,且DM= AC,E为BC延长线上一点,且CE= BC.
(1)(4分)求ME的长;
(2)(4分)求证:△DBE是等腰三角形。
27.(10分)如图,在平面直角坐标系中,满足
(1)(3分)求两点的坐标;
(2)(3分)的平分线与的外角平分线AM交于点C,求的度数;
(3)(4分)在平面内是否存在点P,使为等腰直角三角形?若存在,请写出点P的个数,并直接写出其中两个点的坐标;若不存在,请说明理由.
答案
1-10 DBDDD BABBC
11.= -3 12.4 13.1 14.1440 15. 16.16 17. 18.
19.(1)解:
;
(2)解:
.
20.(1)解:
方程两边乘,得,
解得.
检验:当时,.
所以,原分式方程的解为.
(2)解:
方程两边乘,得,
解得.
检验:当时,,
所以,原分式方程的解为.
21.解:设,,由题意,得或,解得或,当时,等腰三角形的三边为8,8,17,显然不符合三角形的三边关系,当时,等腰三角形的三边长为14,14,5,所以这个等腰三角形的底边长是5,综上所述,这个等腰三角形的底边长是5cm.
22.解:设这个多边形有n条边.
由题意得:(n﹣2)×180°=360°×4,
解得n=10.
故这个多边形的边数是10
23.解:∵AD=BD,∠BAD=34°,
∴∠B=∠BAD=34°,
∵∠ADC是△ABC的外角,
∴∠ADC=∠B+∠BAD=34°+34°=68°,
∵AC=AD,
∴∠C=∠ADC=68°,
∴∠CAB=180°﹣∠B﹣∠C=180°﹣68°﹣34°=78°.
24.(1)证明:连接,
∵,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
又,
∴,
∴,
又,,
∴平分;
(2)解:由(1)知,
∴,
∴,
∵,,
∴,
∵,
∴.
25.(1)证明:在Rt△ADB和△ADC中,
,
∴△ADB≌△ADC(SSS)
(2)证明:∵△ADB≌△ADC,
∴∠DAB=∠DAC,
∵DE∥AC,
∴∠ADE=∠DAC,
∴∠EAD=∠EDA,
∴AE=DE
26.(1)解:∵ AB=AC,AM平分∠BAC,
∴,
∴ME=MC+CE=6.
(2)证明:如图所示:过点D作DN⊥BC,
∵ AB=AC,AM平分∠BAC,
∴AM⊥BC,
∵ D为AC的中点,且DM= AC,DN⊥BC,
∴MN=NC,
∵BM=CE,
∴BN=NE,
∴点D在线段BE的垂直平分线上,
∴BD=DE,
∴△DBE是等腰三角形.
27.(1)解: ,
∴,
,
.
(2)解:平分,平分,
,
,
(3)存在;满足条件的点有6个;或
八年级数学开学学情评估
一、选择题(共30分)
1.(3分)下列交通标志图形中是轴对称图形的是( )
A. B.
C. D.
2.(3分)分式的值为0,则的值是( )
A.0 B. C.4 D.或4
3.(3分)如图,是的角平分线,于点E,,,,则的长是( )
A.9 B.8 C.7 D.6
4.(3分)如图,∠1、∠2、∠3是五边形ABCDE的三个外角,边AE、CD的延长线相交于点F,如果∠F=α,那么∠1+∠2+∠3的度数为( )
A.270°﹣α B.360°﹣α C.90°+α D.180°+α
5.(3分)如图,点E、点F在BC上,BE=CF, ∠B=∠C, 添加一个条件,不能证明△ABF≌△DCE的是( )
A.∠A=∠D B.∠AFB=∠DEC
C.AB=DC D.AF=DE
6.(3分)如图,在中,,,的面积为12,于点,直线垂直平分交于点,交于点,是线段上的一个动点,分别连接,,则的周长的最小值是( )
A.6 B.7 C.10 D.12
7.(3分)若点,关于轴对称,则( )
A.; B.;
C.; D.;
8.(3分)下列运算正确的是( )
A. B.
C. D.
9.(3分)如图,任意画一个的,再分别作的两条角平分线和,和相交于点,连接,有以下结论:①;②平分;③;④;⑤,正确的有( )
A.5个 B.4个 C.3个 D.2个
10.(3分)甲车行驶千米与乙车行驶千米所用时间相同,已知乙车每小时比甲车多行驶千米,设甲车的速度为千米/小时,依题意列方程正确的是( )
A. B.
C. D.
二、填空题(共24分)
11.(3分)当x 时,分式 的值为零.
12.(3分)已知,,则 .
13.(3分)已知和关于x轴对称,则的值为 .
14.(3分)若多边形的每个内角都相等,它的一个外角等于36°,那么这个多边形的内角和等于 °.
15.(3分)如图,中边的垂直平分线分别交、于点、,,的周长为,则的周长是 .
16.(3分)如图,已知中,是边上的中线,为的中点,若的面积为,则的面积为 .
17.(3分)如图,已知△ABC≌△ADE,∠B=25°,∠E=98°,∠EAB=20°,则∠BAD的度数为 .
18.(3分)《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间,设规定时间为x天,则可列出正确的方程为 .
三、因式分解与解方程(共16分)
19.(8分)因式分解:
(1)(4分) (2)(4分)
20.(8分)解方程:
(1)(4分); (2)(4分).
四、解答题(共50分)
21.(6分) 等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,求这个等腰三角形的底边长.
22.(6分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
23.(6分)如图,点D为△ABC的边BC上一点,AC=AD=BD,∠BAD=34°,求∠CAB的度数.
24.(6分)如图,在中,于H,于F,交的延长线于E,且,.
(1)(3分)求证:平分;
(2)(3分)若,求的度数.
25.(8分)如图,在△ABD和△ACD中,AB=AC,BD=CD.
(1)(4分)求证:△ABD≌△ACD;
(2)(4分)过点D作DE∥AC交AB于点E,求证:AE=DE.
26.(8分)如图,在△ABC中,AB=AC, BC=6,AM平分∠BAC,D为AC的中点,且DM= AC,E为BC延长线上一点,且CE= BC.
(1)(4分)求ME的长;
(2)(4分)求证:△DBE是等腰三角形。
27.(10分)如图,在平面直角坐标系中,满足
(1)(3分)求两点的坐标;
(2)(3分)的平分线与的外角平分线AM交于点C,求的度数;
(3)(4分)在平面内是否存在点P,使为等腰直角三角形?若存在,请写出点P的个数,并直接写出其中两个点的坐标;若不存在,请说明理由.
答案
1-10 DBDDD BABBC
11.= -3 12.4 13.1 14.1440 15. 16.16 17. 18.
19.(1)解:
;
(2)解:
.
20.(1)解:
方程两边乘,得,
解得.
检验:当时,.
所以,原分式方程的解为.
(2)解:
方程两边乘,得,
解得.
检验:当时,,
所以,原分式方程的解为.
21.解:设,,由题意,得或,解得或,当时,等腰三角形的三边为8,8,17,显然不符合三角形的三边关系,当时,等腰三角形的三边长为14,14,5,所以这个等腰三角形的底边长是5,综上所述,这个等腰三角形的底边长是5cm.
22.解:设这个多边形有n条边.
由题意得:(n﹣2)×180°=360°×4,
解得n=10.
故这个多边形的边数是10
23.解:∵AD=BD,∠BAD=34°,
∴∠B=∠BAD=34°,
∵∠ADC是△ABC的外角,
∴∠ADC=∠B+∠BAD=34°+34°=68°,
∵AC=AD,
∴∠C=∠ADC=68°,
∴∠CAB=180°﹣∠B﹣∠C=180°﹣68°﹣34°=78°.
24.(1)证明:连接,
∵,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
又,
∴,
∴,
又,,
∴平分;
(2)解:由(1)知,
∴,
∴,
∵,,
∴,
∵,
∴.
25.(1)证明:在Rt△ADB和△ADC中,
,
∴△ADB≌△ADC(SSS)
(2)证明:∵△ADB≌△ADC,
∴∠DAB=∠DAC,
∵DE∥AC,
∴∠ADE=∠DAC,
∴∠EAD=∠EDA,
∴AE=DE
26.(1)解:∵ AB=AC,AM平分∠BAC,
∴,
∴ME=MC+CE=6.
(2)证明:如图所示:过点D作DN⊥BC,
∵ AB=AC,AM平分∠BAC,
∴AM⊥BC,
∵ D为AC的中点,且DM= AC,DN⊥BC,
∴MN=NC,
∵BM=CE,
∴BN=NE,
∴点D在线段BE的垂直平分线上,
∴BD=DE,
∴△DBE是等腰三角形.
27.(1)解: ,
∴,
,
.
(2)解:平分,平分,
,
,
(3)存在;满足条件的点有6个;或
同课章节目录
