几何中的极值与定值问题(二)(广东省深圳市福田区)
文档属性
| 名称 | 几何中的极值与定值问题(二)(广东省深圳市福田区) |  | |
| 格式 | rar | ||
| 文件大小 | 28.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-30 19:35:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
几何中的极值与定值问题(二)
【考点精析】
几何中的极值与定值问题是中考的重点内容,这类问题往往与圆的相关知识、分类讨论问题放在一起综合考查.通过一定量的针对训练,可以锻炼和提高我们的逻辑思维能力和综合分析的能力.
【典型例题】
例1.已知:与互为相反数,且a,b的值恰好为矩形ABCD的长与宽,点P是AD边上的一个动点(P与A,D不重合),以长BC为直径的半圆O交PB于Q点,连结QC(如图).(1)求矩形ABCD的长与宽;(2)设PB=x,△BQC的面积,试求y与x之间的函数关系式,并写出自变量x的取值范围;(3)当最大时,求PB的长.
例2.如图,P是⊙O的直径CB延长线上的一点,PA切⊙O于A.PA=15,PB=5,弦AD交CB于点M.(1)若MA2=MB·MP,试判断CD与AP是否平行,并说明理由;(2)求的值;(3)求AC的长;(4)当D点在BC上移动时,可以得到△ACD的最大面积是多少?
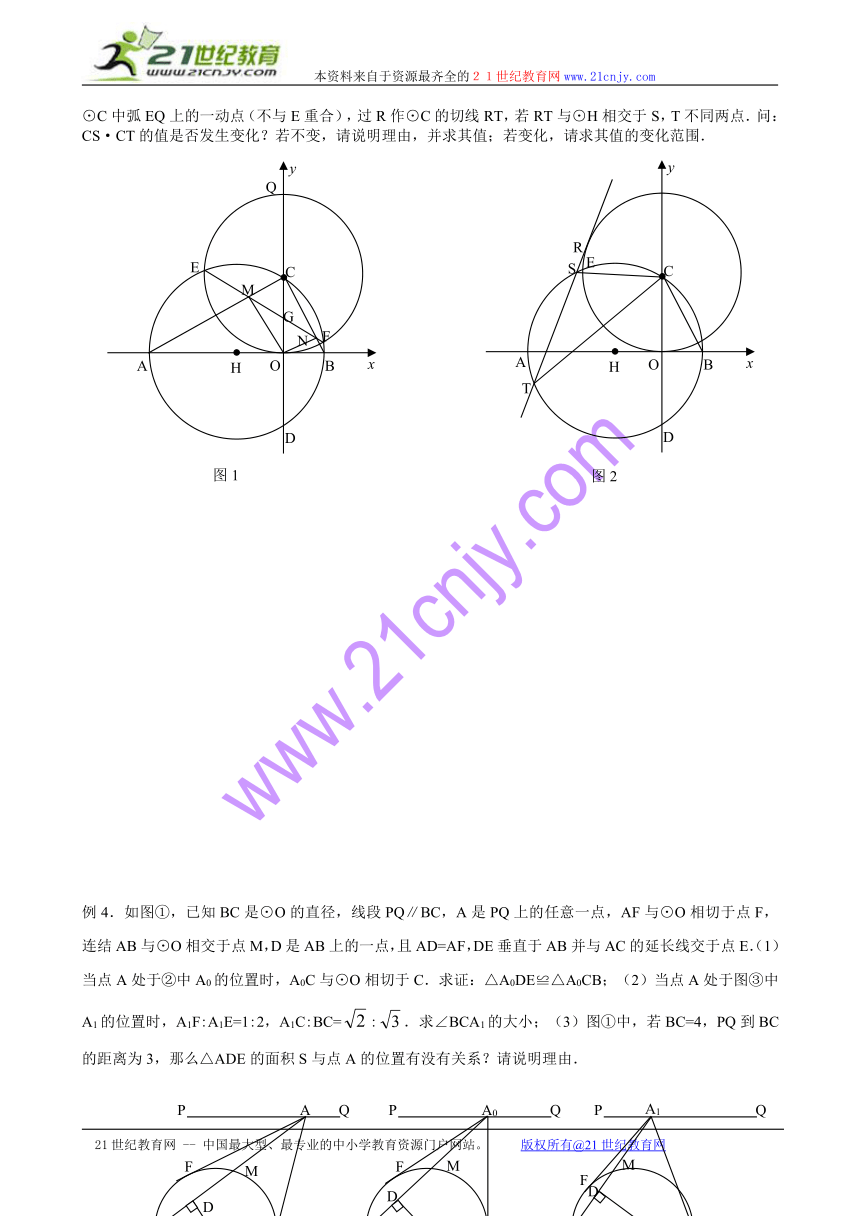
例3.已知,如图1,在直角坐标系xOy中,以x轴的负半轴上一点H为圆心作⊙H与x轴交于A,B两点,与y轴交于C,D两点,以C为圆心,OC为半径作⊙C与⊙H交于E,F两点,与y轴交于O,Q两点.直线EF与AC,BC,y轴分别交于M,N,G三点.直线经过A,C两点.(1)求tan∠CNM的值;(2)连结OM,ON.问四边形CMON是怎样的四边形?请说明理由.(3)如图2,R是⊙C中弧EQ上的一动点(不与E重合),过R作⊙C的切线RT,若RT与⊙H相交于S,T不同两点.问:CS·CT的值是否发生变化?若不变,请说明理由,并求其值;若变化,请求其值的变化范围.
例4.如图①,已知BC是⊙O的直径,线段PQ∥BC,A是PQ上的任意一点,AF与⊙O相切于点F,连结AB与⊙O相交于点M,D是AB上的一点,且AD=AF,DE垂直于AB并与AC的延长线交于点E.(1)当点A处于②中A0的位置时,A0C与⊙O相切于C.求证:△A0DE≌△A0CB;(2)当点A处于图③中A1的位置时,A1F:A1E=1:2,A1C:BC=:.求∠BCA1的大小;(3)图①中,若BC=4,PQ到BC的距离为3,那么△ADE的面积S与点A的位置有没有关系?请说明理由.
【课堂练习】
1.现有一块长为2米,宽为1.2米的矩形木料,要从中裁下两个半径相等的半圆做一圆形桌面,则半圆的最大半径为 米.
2.有一个只有短针和长针的钟,短针OA长6cm,长针OB长8cm,△OAB随着时间的变化不停地改变形状,则△OAB的最大面积是 cm2.
3.如图,由边长为1的25个小正方形组成的正方形网格上有一个△ABC,在网格上画出一个与△ABC相似且面积最大的△A1B1C1,使它的三个顶点都落在小正方形的顶点上,则△A1B1C1的面积是 .
4.如图,这是一个滚珠轴承的平面示意图,若该滚珠轴承的内、外圆周的半径分别为2和6,则在该轴承内最多能放 颗半径均为2的滚珠.
5.如图,长为2cm,宽为1cm的矩形被两个半径为R的圆所覆盖,则R的最小值是 cm,当R取得最小值时,这两个圆的圆心距是 cm.
6.已知:如图,在△ABC中,P是AC上一点,过P,B,C作⊙O交AB于D点,连结DP.(1)求证:△APD∽△ABC;(2)若AB=8,AC=6,BC=4,P是AC上一动点(与A,C不重合),设AP = x,DP2 + PC2 = y,求y与x之间的函数关系式及x的取值范围.(3)由(2)当DP2+PC2=17时,求△APD与△ABC的面积比.
7.如图,△ABC中,AC=6,AB=12,cosA=,M是AB边上的动点,MP∥AC交BC于P,MQ⊥AC于Q,设AM为x,梯形MPCQ的面积是y.(1)求y与x间的函数关系式且指出自变量x的取值范围;(2)梯形MPCQ面积有没有最大值?如果有,请求出这个最大值;如果没有,请说明理由.(3)若使梯形面积为4时,求x的值;(4)画出函数的图像.
8.如图,AB是⊙O的直径,C是圆上不同于A,B的一点,∠ABC=,P在BC上运动,AP与BC相交于D.问:当P位于BC上何处时,能使?并证明你的结论.
9。已知:在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,2),以OA为直径作⊙B.若点D是x轴上的一动点,连结AD交⊙B于点C.
(1)当tan∠DAO=时,求直线BC的解析式;
(2)过点D作DP∥y轴与过B,C两点的直线交于点P,请任意求出三个符合条件的点P的坐标,并确定图像经过这三个点的二次函数的解析式;
(3)若点P满足(2)中的条件,点M的坐标为(-3,3),求线段PM与PB的和的最小值,并求出此时点P的坐标.
A
B
C
D
P
Q
O
A
P
B
M
O
D
C
A
B
H
O
E
C
S
D
x
y
R
T
A
B
H
O
N
F
E
Q
C
M
D
G
x
y
图1
图2
A
Q
P
F
B
C
E
D
M
①
A0
Q
P
F
B
C
E
M
②
A1
Q
P
F
B
C
E
M
③
D
D
C
B
A
题3
题4
题5
题2
A
B
O
A
D
P
O
C
B
Q
A
M
B
P
C
A
B
O
P
D
B
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
几何中的极值与定值问题(二)
【考点精析】
几何中的极值与定值问题是中考的重点内容,这类问题往往与圆的相关知识、分类讨论问题放在一起综合考查.通过一定量的针对训练,可以锻炼和提高我们的逻辑思维能力和综合分析的能力.
【典型例题】
例1.已知:与互为相反数,且a,b的值恰好为矩形ABCD的长与宽,点P是AD边上的一个动点(P与A,D不重合),以长BC为直径的半圆O交PB于Q点,连结QC(如图).(1)求矩形ABCD的长与宽;(2)设PB=x,△BQC的面积,试求y与x之间的函数关系式,并写出自变量x的取值范围;(3)当最大时,求PB的长.
例2.如图,P是⊙O的直径CB延长线上的一点,PA切⊙O于A.PA=15,PB=5,弦AD交CB于点M.(1)若MA2=MB·MP,试判断CD与AP是否平行,并说明理由;(2)求的值;(3)求AC的长;(4)当D点在BC上移动时,可以得到△ACD的最大面积是多少?
例3.已知,如图1,在直角坐标系xOy中,以x轴的负半轴上一点H为圆心作⊙H与x轴交于A,B两点,与y轴交于C,D两点,以C为圆心,OC为半径作⊙C与⊙H交于E,F两点,与y轴交于O,Q两点.直线EF与AC,BC,y轴分别交于M,N,G三点.直线经过A,C两点.(1)求tan∠CNM的值;(2)连结OM,ON.问四边形CMON是怎样的四边形?请说明理由.(3)如图2,R是⊙C中弧EQ上的一动点(不与E重合),过R作⊙C的切线RT,若RT与⊙H相交于S,T不同两点.问:CS·CT的值是否发生变化?若不变,请说明理由,并求其值;若变化,请求其值的变化范围.
例4.如图①,已知BC是⊙O的直径,线段PQ∥BC,A是PQ上的任意一点,AF与⊙O相切于点F,连结AB与⊙O相交于点M,D是AB上的一点,且AD=AF,DE垂直于AB并与AC的延长线交于点E.(1)当点A处于②中A0的位置时,A0C与⊙O相切于C.求证:△A0DE≌△A0CB;(2)当点A处于图③中A1的位置时,A1F:A1E=1:2,A1C:BC=:.求∠BCA1的大小;(3)图①中,若BC=4,PQ到BC的距离为3,那么△ADE的面积S与点A的位置有没有关系?请说明理由.
【课堂练习】
1.现有一块长为2米,宽为1.2米的矩形木料,要从中裁下两个半径相等的半圆做一圆形桌面,则半圆的最大半径为 米.
2.有一个只有短针和长针的钟,短针OA长6cm,长针OB长8cm,△OAB随着时间的变化不停地改变形状,则△OAB的最大面积是 cm2.
3.如图,由边长为1的25个小正方形组成的正方形网格上有一个△ABC,在网格上画出一个与△ABC相似且面积最大的△A1B1C1,使它的三个顶点都落在小正方形的顶点上,则△A1B1C1的面积是 .
4.如图,这是一个滚珠轴承的平面示意图,若该滚珠轴承的内、外圆周的半径分别为2和6,则在该轴承内最多能放 颗半径均为2的滚珠.
5.如图,长为2cm,宽为1cm的矩形被两个半径为R的圆所覆盖,则R的最小值是 cm,当R取得最小值时,这两个圆的圆心距是 cm.
6.已知:如图,在△ABC中,P是AC上一点,过P,B,C作⊙O交AB于D点,连结DP.(1)求证:△APD∽△ABC;(2)若AB=8,AC=6,BC=4,P是AC上一动点(与A,C不重合),设AP = x,DP2 + PC2 = y,求y与x之间的函数关系式及x的取值范围.(3)由(2)当DP2+PC2=17时,求△APD与△ABC的面积比.
7.如图,△ABC中,AC=6,AB=12,cosA=,M是AB边上的动点,MP∥AC交BC于P,MQ⊥AC于Q,设AM为x,梯形MPCQ的面积是y.(1)求y与x间的函数关系式且指出自变量x的取值范围;(2)梯形MPCQ面积有没有最大值?如果有,请求出这个最大值;如果没有,请说明理由.(3)若使梯形面积为4时,求x的值;(4)画出函数的图像.
8.如图,AB是⊙O的直径,C是圆上不同于A,B的一点,∠ABC=,P在BC上运动,AP与BC相交于D.问:当P位于BC上何处时,能使?并证明你的结论.
9。已知:在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,2),以OA为直径作⊙B.若点D是x轴上的一动点,连结AD交⊙B于点C.
(1)当tan∠DAO=时,求直线BC的解析式;
(2)过点D作DP∥y轴与过B,C两点的直线交于点P,请任意求出三个符合条件的点P的坐标,并确定图像经过这三个点的二次函数的解析式;
(3)若点P满足(2)中的条件,点M的坐标为(-3,3),求线段PM与PB的和的最小值,并求出此时点P的坐标.
A
B
C
D
P
Q
O
A
P
B
M
O
D
C
A
B
H
O
E
C
S
D
x
y
R
T
A
B
H
O
N
F
E
Q
C
M
D
G
x
y
图1
图2
A
Q
P
F
B
C
E
D
M
①
A0
Q
P
F
B
C
E
M
②
A1
Q
P
F
B
C
E
M
③
D
D
C
B
A
题3
题4
题5
题2
A
B
O
A
D
P
O
C
B
Q
A
M
B
P
C
A
B
O
P
D
B
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
