2015人教版数学八上第11章《三角形》复习小结PPT课件(共15张PPT)
文档属性
| 名称 | 2015人教版数学八上第11章《三角形》复习小结PPT课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 214.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-04 15:12:23 | ||
图片预览






文档简介
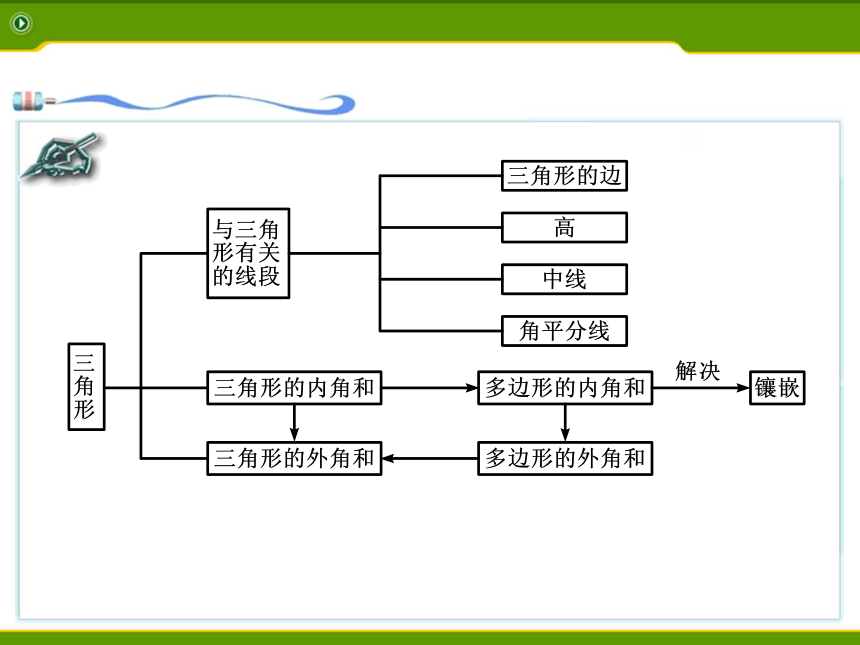
课件15张PPT。复习小结 【问题1】本章学习了哪些知识?它们之间的联系是什么?例1 下列长度的三条线段能组成三角形的是( )
A.1cm,2cm,3.5cm
B.4cm,5cm,9cm
C.5cm,8cm,15cm
D.6cm,8cm,9cm
【问题2】三角形的三边的关系是什么?
D 例2 一个三角形的两条边的长分别为3和5.
⑴求第三边 x 的长的取值范围;
⑵若这个三角形是等腰三角形,求这个三角形的周长.解:当腰长为3时,这个三角形的周长为11; 当腰长为5时,这个三角形的周长为13.【问题3】怎样运用三角形的内角和定理及外角性质解决问题?例3 ⑴在△ABC中,∠A=3∠B=120°,
求∠C 的度数. ⑵ 如图,已知AC∥ED,∠C=26°,
∠BED=63°,求∠B 的度数.解:∵ AC∥ED,∴ ∠ CAE=∠BED=63°.∵ ∠ CAE=∠B+ ∠C,∴ ∠C= ∠ CAE -∠B=63°-26°=37°.【问题4】应用多边形的内角和、外角和解决哪些问题?例4 ⑴若一个多边形的内角和与它的外角和之和是1 800°,这个多边形的边数.解:设这个多边形的边数为n,由题意得解得所以这个多边形是十边形. ⑵如图,小陈从O点出发,前进了5米后向右转20°的角,再前进5米后又向右转20°,…,这样一直走下去,他第一次回到出发点O时一共走了多少米?O解:由题意可知这个正多边形 的每个外角都是20°. 360°÷20°=18. 5×18=90(米).【问题5】三角形的三条重要线段有哪些?例5 如图,AD是△ABC的高, ∠C=65°, ∠ABD=∠BAD,求∠BAC的度数.解:∵ AD是△ABC的高,∴ ∠ ADC=90°,∴ ∠DAC=25°.∵ ∠ ADC=∠B+ ∠BAD=90°,∴ ∠BAD= 45°,∠ABD=∠BAD,∴ ∠ BAD=∠CAD+ ∠BAD=45°+25°=70°. 例6 如图a,在△ABC中,∠ABC、∠ACB的平分线相交于点O .①若∠ABC= 40°,∠ACB=50°,
则∠BOC的度数为 ; ②若∠A=76°,则∠BOC
的度数为 ;135°128° ③你能找出∠A与∠BOC之间的数量关系吗?说明理由.解: (2)如图b,点O是△ABC的两外角平分线BO、CO的交点,那么∠BOC与∠A有怎样的数量关系?并说明理由.解:你有什么收获?作业
A.1cm,2cm,3.5cm
B.4cm,5cm,9cm
C.5cm,8cm,15cm
D.6cm,8cm,9cm
【问题2】三角形的三边的关系是什么?
D 例2 一个三角形的两条边的长分别为3和5.
⑴求第三边 x 的长的取值范围;
⑵若这个三角形是等腰三角形,求这个三角形的周长.解:当腰长为3时,这个三角形的周长为11; 当腰长为5时,这个三角形的周长为13.【问题3】怎样运用三角形的内角和定理及外角性质解决问题?例3 ⑴在△ABC中,∠A=3∠B=120°,
求∠C 的度数. ⑵ 如图,已知AC∥ED,∠C=26°,
∠BED=63°,求∠B 的度数.解:∵ AC∥ED,∴ ∠ CAE=∠BED=63°.∵ ∠ CAE=∠B+ ∠C,∴ ∠C= ∠ CAE -∠B=63°-26°=37°.【问题4】应用多边形的内角和、外角和解决哪些问题?例4 ⑴若一个多边形的内角和与它的外角和之和是1 800°,这个多边形的边数.解:设这个多边形的边数为n,由题意得解得所以这个多边形是十边形. ⑵如图,小陈从O点出发,前进了5米后向右转20°的角,再前进5米后又向右转20°,…,这样一直走下去,他第一次回到出发点O时一共走了多少米?O解:由题意可知这个正多边形 的每个外角都是20°. 360°÷20°=18. 5×18=90(米).【问题5】三角形的三条重要线段有哪些?例5 如图,AD是△ABC的高, ∠C=65°, ∠ABD=∠BAD,求∠BAC的度数.解:∵ AD是△ABC的高,∴ ∠ ADC=90°,∴ ∠DAC=25°.∵ ∠ ADC=∠B+ ∠BAD=90°,∴ ∠BAD= 45°,∠ABD=∠BAD,∴ ∠ BAD=∠CAD+ ∠BAD=45°+25°=70°. 例6 如图a,在△ABC中,∠ABC、∠ACB的平分线相交于点O .①若∠ABC= 40°,∠ACB=50°,
则∠BOC的度数为 ; ②若∠A=76°,则∠BOC
的度数为 ;135°128° ③你能找出∠A与∠BOC之间的数量关系吗?说明理由.解: (2)如图b,点O是△ABC的两外角平分线BO、CO的交点,那么∠BOC与∠A有怎样的数量关系?并说明理由.解:你有什么收获?作业
