人教版七下第五章《相交线与平行线》单元测试卷(含答案)
文档属性
| 名称 | 人教版七下第五章《相交线与平行线》单元测试卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五章相交线与平行线单元测试卷
时间100分钟 满分120分
姓名 班级 考号
一、选择题(每小题3分,共36分)
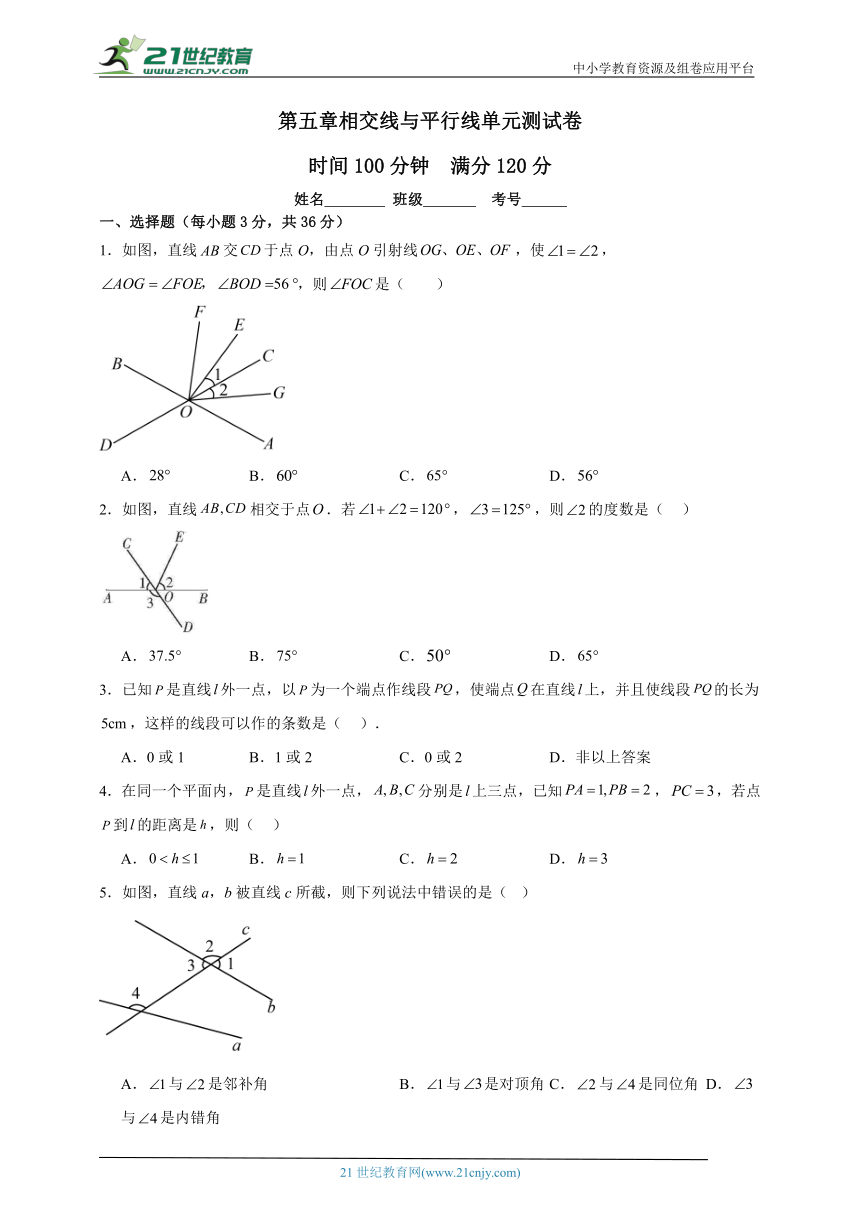
1.如图,直线交于点O,由点O引射线,使,,则是( )
A. B. C. D.
2.如图,直线相交于点.若,,则的度数是( )
A. B. C. D.
3.已知是直线外一点,以为一个端点作线段,使端点在直线上,并且使线段的长为,这样的线段可以作的条数是( ).
A.0或1 B.1或2 C.0或2 D.非以上答案
4.在同一个平面内,是直线外一点,分别是上三点,已知,,若点到的距离是,则( )
A. B. C. D.
5.如图,直线a,b被直线c所截,则下列说法中错误的是( )
A.与是邻补角 B.与是对顶角 C.与是同位角 D.与是内错角
6.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行 B.相等的角是对顶角
C.如果两个角的和是180°,那么这两个角互为余角 D.同角或等角的余角相等
7.下列说法中,正确的是( )
A.互为补角的两个角可以都是锐角 B.过直线外一点有且只有一条直线与这条直线平行
C.同一平面内,若且,则 D.过一点有且只有一条直线与已知直线垂直
8.如图,点E在的延长线上,下列条件能判断的是( )
A. B.
C. D.
9.如图,下列条件中,不能判断直线的是( )
A. B. C. D.
10.在同一平面内,a、b、c是直线,下列说法正确的是( )
A.若, 则 B.若,,则
C.若,,则 D.若,,则
11.一块含角的直角三角板,按如图所示方式放置,顶点A,分别落在直线,上,若直线,,则的度数是( )
A. B. C. D.
12.小方、小辉、小明、小杰一起研究一道数学题.如图所示,已知,,是边上一点(不与,重合).
小方说:“如果还知道,则能得到”;
小辉说:“把小方的已知和结论倒过来,即由,可得到”;
小明说:“一定大于”;
小杰说:“如果连接,则一定平行于”.
他们四人中,有几个人的说法是正确的?( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分)
13.如图,直线、相交于点G,,平分,若,则 °.
14.在同一平面内,若直线a∥c,b∥c,则a b.
15.一副三角板按如图所示(共顶点A)叠放在一起,若固定三角板,改变三角板的位置(其中A点位置始终不变),当 时,.
16.如图,有下列说法:①若,则;②若,则;③若,则;④若,则.其中说法正确的有 个.
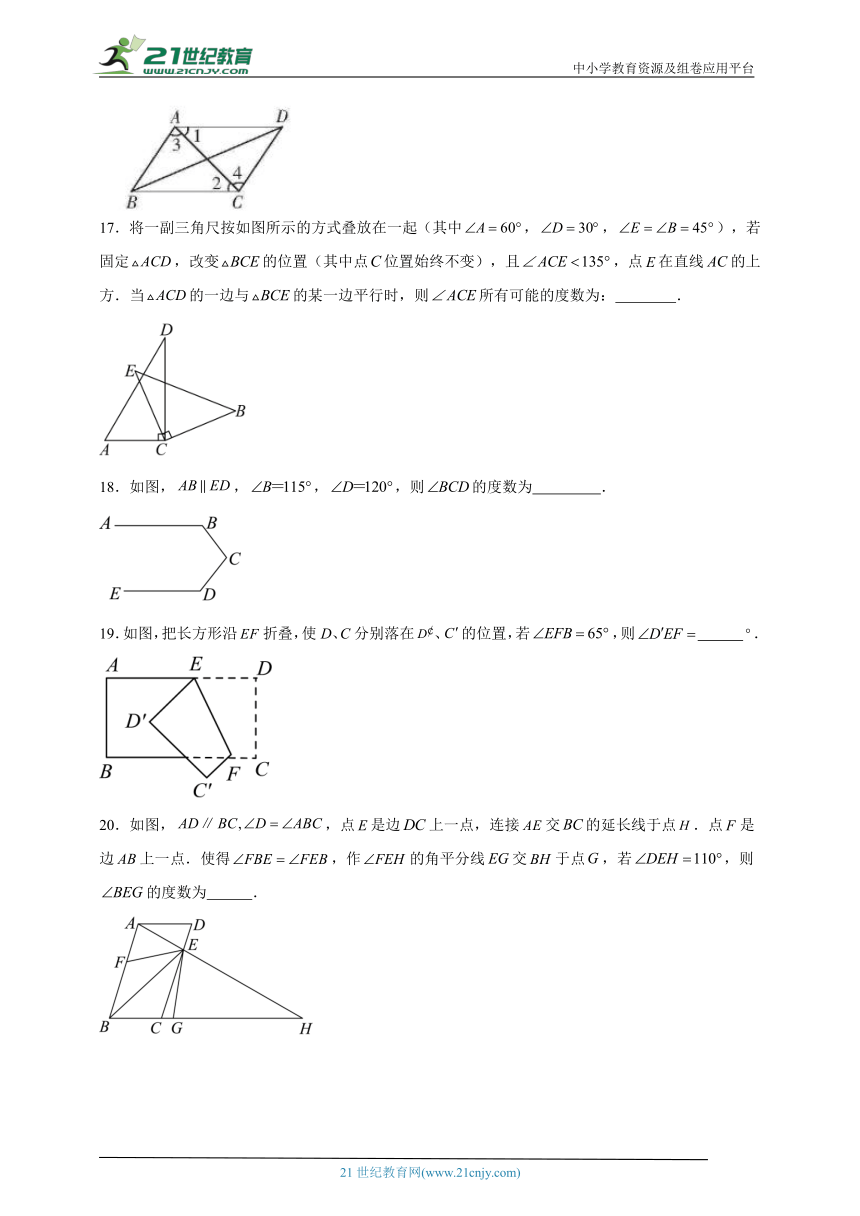
17.将一副三角尺按如图所示的方式叠放在一起(其中,,),若固定,改变的位置(其中点位置始终不变),且,点在直线的上方.当的一边与的某一边平行时,则所有可能的度数为: .
18.如图,,,,则的度数为 .
19.如图,把长方形沿折叠,使D、C分别落在、的位置,若,则 .
20.如图,,点是边上一点,连接交的延长线于点.点是边上一点.使得,作的角平分线交于点,若,则的度数为 .
三、解答题(共60分)
21.(7分)如图,点,,在同一条直线上,,,分别是,的平分线.
(1)若,求的度数;
(2)若,求的度数.
22.(7分)如图,已知直线被直线所截,平分,平分,,吗?为什么?
因为平分,平分(已知),
所以___________,___________,
所以___________( ),
因为( ),
所以___________,
所以( ).
23.(8分)如图,,,平分,,.求的度数.
24.(8分)如图1是一盏可折叠台灯.图2、图3是其平面示意图,支架、为固定支撑杆,支架可绕点C旋转调节.已知灯体顶角,顶角平分线始终与垂直.
(1)如图2,当支架旋转至水平位置时,恰好与平行,求支架与水平方向的夹角的度数;
(2)若将图2中的绕点顺时针旋转到如图3的位置,求此时与水平方向的夹角的度数.
25.(10分)如图,已知:中,D、E、F、G分别在、和上,连接、和,,.
(1)判断与的位置关系,并证明;
(2)若,,求的度数.
26.(10分)如图,已知,.
(1)与平行吗?请说明理由.
(2)若平分,于点A,,求的度数.
27.(10分)如图,已知直线,,点、在边上,且满足,平分.
(1)求的度数;
(2)若平行移动,那么:的值是否随之发生变化?若变化,请找出变化的规律;若不变,求出这个比值.
第五章单元测试卷参考答案
1.D[提示:
故选:.]
2.D
3.D[提示:当与的距离小于时,这样的线段可作条;
当与的距离等于时,这样的线段可作条;
当与的距离大于时,这样的线段可作条;
综上,这样的线段可作条或条或条,
故选:.]
4.A[提示:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离,即.
故选:A.]
5.D[提示:A、与有一条公共边,另一边互为反向延长线,故A正确;
B、与的两边互为反向延长线,故B正确;
C、与的位置相同,故C正确;
D、与是同旁内角.故D错误;
故选:D.]
6.D
7.B[提示:A.互为补角的两个角不可能都是锐角,故A不符合题意;
B.过直线外一点有且只有一条直线与这条直线平行,故B符合题意;
C.同一平面内,若且,则,故C不符合题意;
D.平面内,过一点有且只有一条直线与已知直线垂直,故D不符合题意;
故选:B.]
8.A[提示:A. ∵,∴,符合题意;
B. ∵,∴,不合题意;
C. ∵,∴,不合题意;
D. ∵∴,不合题意.
故选:A]
9.D[提示:A、∵,
∴(同旁内角互补,两直线平行),故A不符合题意;
B、∵,
∴(内错角相等,两直线平行),故B不符合题意;
C、∵,
∴(同位角相等,两直线平行),故C不符合题意;
D、根据不能判断直线,故D符合题意;
故选:D.]
10.A[提示:A.在同一平面内,若,则正确,故本选项正确;
B.在同一平面内,若,则,故本选项错误;
C.在同一平面内,若,则,故本选项错误;
D.在同一平面内,若,则,故本选项错误.
故选:A.]
11.D[提示:如图:过点B作,
∵,
∴,
∴,
∴,
∴.
故选:D.]
12.B[提示:已知,,
∴,
∴,
小方:若,
∴,
∴,
∴,故小方的说法是正确的;
小辉:若,
∴,
∴,
∵,
∴,故小辉的说法是正确的;
小明:不一定大于,故小明的说法是不正确的;
小杰:如果连接,则不一定平行于,故小杰的说法是不正确的;
综上所述,正确的说法有2个.
故选B.]
13.30[提示:∵,
∴设,,
∴,
∵,
∴,
∴,
∵平分 ,
∴,
∴,
解得:,
∴,
∴,
故答案为:30.]
14.∥[提示:∵a∥c,b∥c,
∴a∥b(平行于同一直线的两条直线互相平行).
故答案为:∥.]
15.30或150[提示:由题意得,,
①如图,
当时,可得;
②如图,
当时,可得,
则.
故答案为:30或150.]
16.1
17.或或[提示:①当时,
∵,
∴,
∴,
∴;
②当时,如图,
∵,
∴;
③当时,如图,
∵,
∴,
∴;
④当时,如图,
∵,
∴,
∴;
综上所述:当或或时,有一组边互相平行.
故答案为:或或.]
18./125度[提示:如图,过点C作,
∵,
∴,
∴,,
∵,,
∴,,
∴,
故答案为:.]
19.[提示:∵,
∴,
由折叠的性质知,,
故答案为:.]
20./35度[提示:,,
,
的角平分线为,
,
,
,
而,
,
,
,
,
,
,
,
.
故答案为:]
21.解:(1)根据题意,
得到,
∵,分别是,的平分线
∴.
∵,
∴;
(2)∵,,
∴,
∵
∴.
22.解:因为平分,平分(已知),
所以,,
所以(等式的性质),
因为(已知),
所以,
所以(同旁内角互补,两直线平行).
23.解:∵,,
∴,
∴,
∵,,
∴,
∵平分,
∴,
∵,
∴.
24.(1)解:如图2,,平分,
,
,
,
,
,
,
,
,
即;
(2)如图3,过点作,过点作,
则,
,
,
,,
,
,
.
25.(1)解:,理由如下:
∵,
∴,
∴,
又∵,
∴,
∴;
(2)解:由(1)可知,,,
∵,
∴,
∵,
∴,
∵,
∴,
∴.
26.解:(1)与平行,理由如下:
,
,
,
,
,
;
(2),,
,
平分,
,
,
,
,
,
.
27.(1)解:∵,,
,
,平分,
,,
,
∴,即,
;
(2)解:不变化
因为平行移动,
∵,
,
∵,
,
:的值恒等于:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第五章相交线与平行线单元测试卷
时间100分钟 满分120分
姓名 班级 考号
一、选择题(每小题3分,共36分)
1.如图,直线交于点O,由点O引射线,使,,则是( )
A. B. C. D.
2.如图,直线相交于点.若,,则的度数是( )
A. B. C. D.
3.已知是直线外一点,以为一个端点作线段,使端点在直线上,并且使线段的长为,这样的线段可以作的条数是( ).
A.0或1 B.1或2 C.0或2 D.非以上答案
4.在同一个平面内,是直线外一点,分别是上三点,已知,,若点到的距离是,则( )
A. B. C. D.
5.如图,直线a,b被直线c所截,则下列说法中错误的是( )
A.与是邻补角 B.与是对顶角 C.与是同位角 D.与是内错角
6.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行 B.相等的角是对顶角
C.如果两个角的和是180°,那么这两个角互为余角 D.同角或等角的余角相等
7.下列说法中,正确的是( )
A.互为补角的两个角可以都是锐角 B.过直线外一点有且只有一条直线与这条直线平行
C.同一平面内,若且,则 D.过一点有且只有一条直线与已知直线垂直
8.如图,点E在的延长线上,下列条件能判断的是( )
A. B.
C. D.
9.如图,下列条件中,不能判断直线的是( )
A. B. C. D.
10.在同一平面内,a、b、c是直线,下列说法正确的是( )
A.若, 则 B.若,,则
C.若,,则 D.若,,则
11.一块含角的直角三角板,按如图所示方式放置,顶点A,分别落在直线,上,若直线,,则的度数是( )
A. B. C. D.
12.小方、小辉、小明、小杰一起研究一道数学题.如图所示,已知,,是边上一点(不与,重合).
小方说:“如果还知道,则能得到”;
小辉说:“把小方的已知和结论倒过来,即由,可得到”;
小明说:“一定大于”;
小杰说:“如果连接,则一定平行于”.
他们四人中,有几个人的说法是正确的?( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分)
13.如图,直线、相交于点G,,平分,若,则 °.
14.在同一平面内,若直线a∥c,b∥c,则a b.
15.一副三角板按如图所示(共顶点A)叠放在一起,若固定三角板,改变三角板的位置(其中A点位置始终不变),当 时,.
16.如图,有下列说法:①若,则;②若,则;③若,则;④若,则.其中说法正确的有 个.
17.将一副三角尺按如图所示的方式叠放在一起(其中,,),若固定,改变的位置(其中点位置始终不变),且,点在直线的上方.当的一边与的某一边平行时,则所有可能的度数为: .
18.如图,,,,则的度数为 .
19.如图,把长方形沿折叠,使D、C分别落在、的位置,若,则 .
20.如图,,点是边上一点,连接交的延长线于点.点是边上一点.使得,作的角平分线交于点,若,则的度数为 .
三、解答题(共60分)
21.(7分)如图,点,,在同一条直线上,,,分别是,的平分线.
(1)若,求的度数;
(2)若,求的度数.
22.(7分)如图,已知直线被直线所截,平分,平分,,吗?为什么?
因为平分,平分(已知),
所以___________,___________,
所以___________( ),
因为( ),
所以___________,
所以( ).
23.(8分)如图,,,平分,,.求的度数.
24.(8分)如图1是一盏可折叠台灯.图2、图3是其平面示意图,支架、为固定支撑杆,支架可绕点C旋转调节.已知灯体顶角,顶角平分线始终与垂直.
(1)如图2,当支架旋转至水平位置时,恰好与平行,求支架与水平方向的夹角的度数;
(2)若将图2中的绕点顺时针旋转到如图3的位置,求此时与水平方向的夹角的度数.
25.(10分)如图,已知:中,D、E、F、G分别在、和上,连接、和,,.
(1)判断与的位置关系,并证明;
(2)若,,求的度数.
26.(10分)如图,已知,.
(1)与平行吗?请说明理由.
(2)若平分,于点A,,求的度数.
27.(10分)如图,已知直线,,点、在边上,且满足,平分.
(1)求的度数;
(2)若平行移动,那么:的值是否随之发生变化?若变化,请找出变化的规律;若不变,求出这个比值.
第五章单元测试卷参考答案
1.D[提示:
故选:.]
2.D
3.D[提示:当与的距离小于时,这样的线段可作条;
当与的距离等于时,这样的线段可作条;
当与的距离大于时,这样的线段可作条;
综上,这样的线段可作条或条或条,
故选:.]
4.A[提示:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离,即.
故选:A.]
5.D[提示:A、与有一条公共边,另一边互为反向延长线,故A正确;
B、与的两边互为反向延长线,故B正确;
C、与的位置相同,故C正确;
D、与是同旁内角.故D错误;
故选:D.]
6.D
7.B[提示:A.互为补角的两个角不可能都是锐角,故A不符合题意;
B.过直线外一点有且只有一条直线与这条直线平行,故B符合题意;
C.同一平面内,若且,则,故C不符合题意;
D.平面内,过一点有且只有一条直线与已知直线垂直,故D不符合题意;
故选:B.]
8.A[提示:A. ∵,∴,符合题意;
B. ∵,∴,不合题意;
C. ∵,∴,不合题意;
D. ∵∴,不合题意.
故选:A]
9.D[提示:A、∵,
∴(同旁内角互补,两直线平行),故A不符合题意;
B、∵,
∴(内错角相等,两直线平行),故B不符合题意;
C、∵,
∴(同位角相等,两直线平行),故C不符合题意;
D、根据不能判断直线,故D符合题意;
故选:D.]
10.A[提示:A.在同一平面内,若,则正确,故本选项正确;
B.在同一平面内,若,则,故本选项错误;
C.在同一平面内,若,则,故本选项错误;
D.在同一平面内,若,则,故本选项错误.
故选:A.]
11.D[提示:如图:过点B作,
∵,
∴,
∴,
∴,
∴.
故选:D.]
12.B[提示:已知,,
∴,
∴,
小方:若,
∴,
∴,
∴,故小方的说法是正确的;
小辉:若,
∴,
∴,
∵,
∴,故小辉的说法是正确的;
小明:不一定大于,故小明的说法是不正确的;
小杰:如果连接,则不一定平行于,故小杰的说法是不正确的;
综上所述,正确的说法有2个.
故选B.]
13.30[提示:∵,
∴设,,
∴,
∵,
∴,
∴,
∵平分 ,
∴,
∴,
解得:,
∴,
∴,
故答案为:30.]
14.∥[提示:∵a∥c,b∥c,
∴a∥b(平行于同一直线的两条直线互相平行).
故答案为:∥.]
15.30或150[提示:由题意得,,
①如图,
当时,可得;
②如图,
当时,可得,
则.
故答案为:30或150.]
16.1
17.或或[提示:①当时,
∵,
∴,
∴,
∴;
②当时,如图,
∵,
∴;
③当时,如图,
∵,
∴,
∴;
④当时,如图,
∵,
∴,
∴;
综上所述:当或或时,有一组边互相平行.
故答案为:或或.]
18./125度[提示:如图,过点C作,
∵,
∴,
∴,,
∵,,
∴,,
∴,
故答案为:.]
19.[提示:∵,
∴,
由折叠的性质知,,
故答案为:.]
20./35度[提示:,,
,
的角平分线为,
,
,
,
而,
,
,
,
,
,
,
,
.
故答案为:]
21.解:(1)根据题意,
得到,
∵,分别是,的平分线
∴.
∵,
∴;
(2)∵,,
∴,
∵
∴.
22.解:因为平分,平分(已知),
所以,,
所以(等式的性质),
因为(已知),
所以,
所以(同旁内角互补,两直线平行).
23.解:∵,,
∴,
∴,
∵,,
∴,
∵平分,
∴,
∵,
∴.
24.(1)解:如图2,,平分,
,
,
,
,
,
,
,
,
即;
(2)如图3,过点作,过点作,
则,
,
,
,,
,
,
.
25.(1)解:,理由如下:
∵,
∴,
∴,
又∵,
∴,
∴;
(2)解:由(1)可知,,,
∵,
∴,
∵,
∴,
∵,
∴,
∴.
26.解:(1)与平行,理由如下:
,
,
,
,
,
;
(2),,
,
平分,
,
,
,
,
,
.
27.(1)解:∵,,
,
,平分,
,,
,
∴,即,
;
(2)解:不变化
因为平行移动,
∵,
,
∵,
,
:的值恒等于:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
