2024年河南省郑州市中考模拟数学试卷(二)(含答案)
文档属性
| 名称 | 2024年河南省郑州市中考模拟数学试卷(二)(含答案) | 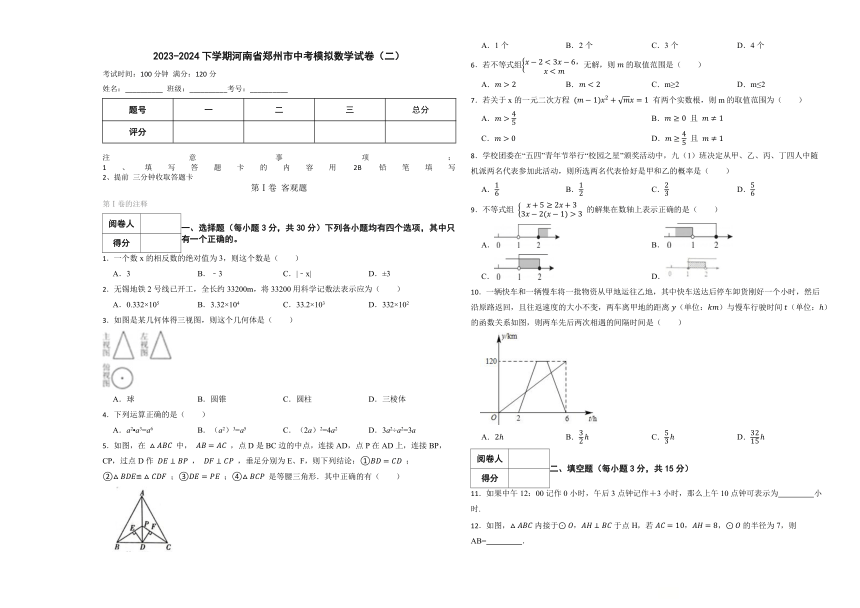 | |
| 格式 | docx | ||
| 文件大小 | 346.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 20:46:24 | ||
图片预览

文档简介
2023-2024下学期河南省郑州市中考模拟数学试卷(二)
考试时间:100分钟 满分:120分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 三分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个正确的。
得分
1.一个数x的相反数的绝对值为3,则这个数是( )
A.3 B.﹣3 C.|﹣x| D.±3
2.无锡地铁2号线已开工,全长约33200m,将33200用科学记数法表示应为( )
A.0.332×105 B.3.32×104 C.33.2×103 D.332×102
3.如图是某几何体得三视图,则这个几何体是( )
A.球 B.圆锥 C.圆柱 D.三棱体
4.下列运算正确的是( )
A.a2 a3=a6 B.(a2)3=a5 C.(2a)2=4a2 D.3a2÷a2=3a
5.如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.若不等式组无解,则的取值范围是( )
A. B. C.m≥2 D.m≤2
7.若关于x的一元二次方程 有两个实数根,则m的取值范围为( )
A. B. 且
C. D. 且
8.学校团委在“五四”青年节举行“校园之星”颁奖活动中,九(1)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则所选两名代表恰好是甲和乙的概率是( )
A. B. C. D.
9.不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
10.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后停车卸货刚好一个小时,然后沿原路返回,且往返速度的大小不变,两车离甲地的距离(单位:)与慢车行驶时间(单位:)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A. B. C. D.
阅卷人 二、填空题(每小题3分,共15分)
得分
11.如果中午12:00记作0小时,午后3点钟记作+3小时,那么上午10点钟可表示为 小时.
12.如图,内接于于点H,若,的半径为7,则AB= .
13.已知样本x1,x2,x3,…,x2014的方差是2,那么样本3x1-1,3x2-1,3x3-1,…,3x2014-1的方差是 .
14.如图是一个正六边形的飞镖游戏板,顺次连接三个不相邻的顶点将正六边形分成4个区域。向该游戏板投掷飞镖一次(假设飞镖落在游戏板上,且落在游戏板上的位置是随机的),则飞镖落在阴影区域的概率是 .
15.如图,在矩形中,,,点,分别在边,上,且,按以下步骤操作:
第一步,沿直线翻折,点的对应点恰好落在对角线上,点的对应点为,则 ;
第二步,分别在,上取点,,沿直线继续翻折,使点与点重合,则线段的长为 .
阅卷人 三、解答题(本大题共8个小题,共75分)
得分
16.计算:
(1)
(2)
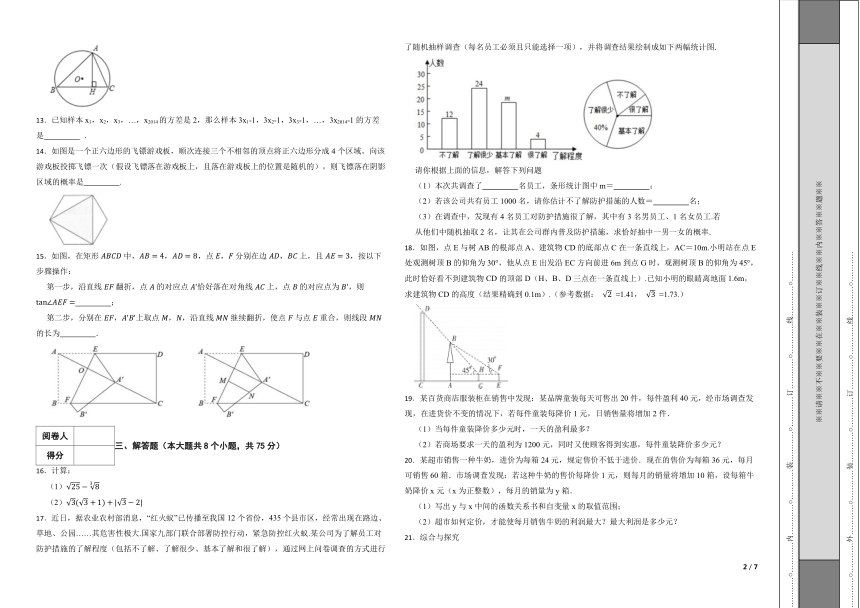
17.近日,据农业农村部消息,“红火蚁”已传播至我国12个省份,435个县市区,经常出现在路边、草地、公园……其危害性极大.国家九部门联合部署防控行动,紧急防控红火蚁.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
请你根据上面的信息,解答下列问题
(1)本次共调查了 名员工,条形统计图中m= ;
(2)若该公司共有员工1000名,请你估计不了解防护措施的人数= 名;
(3)在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若
从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
18.如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)
19.某百货商店服装柜在销售中发现:某品牌童装每天可售出20件,每件盈利40元,经市场调查发现,在进货价不变的情况下,若每件童装每降价1元,日销售量将增加2件.
(1)当每件童装降价多少元时,一天的盈利最多?
(2)若商场要求一天的盈利为1200元,同时又使顾客得到实惠,每件童装降价多少元?
20.某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系书和自变量x的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
21.综合与探究
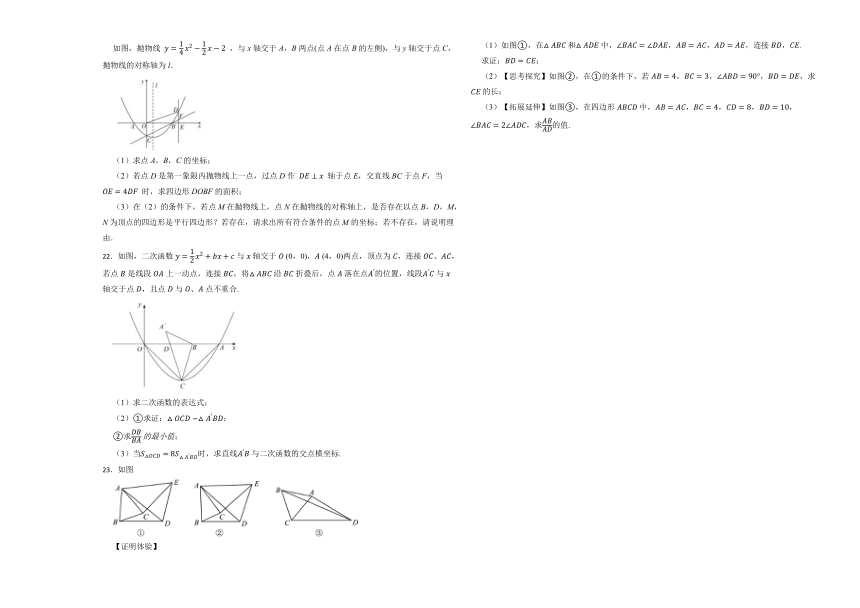
如图,抛物线 ,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴为l.
(1)求点A,B,C的坐标;
(2)若点D是第一象限内抛物线上一点,过点D作 轴于点E,交直线BC于点F,当 时,求四边形DOBF的面积;
(3)在(2)的条件下,若点M在抛物线上,点N在抛物线的对称轴上,是否存在以点B,D,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
22.如图,二次函数与轴交于 (0,0), (4,0)两点,顶点为,连接、,若点是线段上一动点,连接,将沿折叠后,点落在点的位置,线段与轴交于点,且点与、点不重合.
(1)求二次函数的表达式;
(2)①求证:;
②求;
(3)当时,求直线与二次函数的交点横坐标.
23.如图
【证明体验】
(1)如图①,在和中,,,,连接,.
求证:;
(2)【思考探究】如图②,在①的条件下,若,,,,求的长;
(3)【拓展延伸】如图③,在四边形中,,,,,,求的值.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】-2
12.【答案】
13.【答案】2
14.【答案】
15.【答案】2;
16.【答案】(1)解:
=3
(2)解:
=5
17.【答案】(1)60;20
(2)200
(3)解:根据题意,列表如下:
第1名 第2名
女
女
由上表可知,共有12种结果,每种结果出现的可能性都相等,其中恰好抽中一男一女的结果有6种,
故所求概率为 .
18.【答案】解:如图,延长FH,交CD于点M,交AB于点N,
∵ ∠BHN=45°,BA⊥MH,
则BN=NH,
设BN=NH=x,
∵ HF=6,∠BFN=30°,且tan∠BFN= = ,
∴tan30°= ,
解得x≈8.22,
根据题意可知:
DM=MH=MN+NH,
∵ MN=AC=10,
则DM=10+8.22=18.22,
∴ CD=DM+MC=DM+EF=18.22+1.6=19.82≈19.8(m).
答:建筑物CD的高度约为19.8m.
19.【答案】(1)解:设每件童装降价x元,则每天盈利为S,
则S=(40﹣x)(2x+20)=﹣2x2+60x+800,
当x==15时,S有最大值为1250元;
(2)解:一天盈利为1200元,则
S=﹣2x2+60x+800=1200,
整理得:﹣2x2+60x﹣400=0,
a=﹣2,b=60,c=﹣400,
b2﹣4ac=3600﹣(4×2×400)=400>0,
解得:x1=20,x2=10,(舍去)
∴每件童装降价20元.
20.【答案】(1)解:根据题意,得:y=60+10x,
由36﹣x≥24得x≤12,
∴1≤x≤12,且x为整数
(2)解:设所获利润为W,
则W=(36﹣x﹣24)(10x+60)
=﹣10x2+60x+720
=﹣10(x﹣3)2+810,
∴当x=3时,W取得最大值,最大值为810,
答:超市定价为33元时,才能使每月销售牛奶的利润最大,最大利润是810元
21.【答案】(1)解:由 ,得 .
解方程,得 , .
∵点A在点B的左侧,∴点A的坐标为(-2,0),点B的坐标为(4,0).
由 ,得 ,∴点C的坐标为(0,-2)
(2)解:设直线BC的函数表达式为 ,经过点B(4,0),C(0,-2),∴ 解得 ,∴直线BC的函数表达式为 .
设点D的坐标为 ,则点F的坐标为 ,点E的坐标为(m,0).
∵点D在第一象限,∴ .
又∵ ,∴ .
解得 , (舍去),∴点E的坐标为(5,0),点D的坐标为 ,点F的坐标为 ,∴ .
(3)解:设点N的坐标为(1,n),
①当NB为对角线时,如答图1所示,
点M的坐标为 .
代入 ,得 ,解得 .
此时点M的坐标为(0,-2);
②当ND为对角线时,如答图2所示,
点M的坐标为 ,
代入 ,得 .
解得 .
此时点M的坐标为(2,-2);
③当BD为对角线时,如答图3所示,
点M的坐标为 ,
代入 ,得 .
解得 .
此时点M的坐标为(8,10).
综上所述:存在以点B,D,M,N为顶点的四边形是平行四边形,点M的坐标分别为(0,-2)或(2,-2)或(8,10).
22.【答案】(1)解:∵二次函数与轴交于 (0,0), (4,0)两点,
∴代入 (0,0), (4,0)得,,
解得:,
∴二次函数的表达式为;
(2)解:①证明:∵=,
∴顶点C的坐标是(2,﹣2),抛物线的对称轴为直线x=2,
∵二次函数与轴交于(0,0),(4,0)两点,
∴由抛物线的对称性可知OC=AC,
∴∠CAB=∠COD,
∵沿折叠后,点落在点的位置,线段与轴交于点,
∴ △ABC≌△BC,
∴∠CAB=∠,AB=B,
∴∠COD=∠,
∵∠ODC=∠BD,
∴;
②∵,
∴,
设点D的坐标为(d,0),
由两点间距离公式得DC=,
∵点与、点不重合,
∴0<d<4,
对于 =来说,
∵ a=1>0,
∴抛物线开口向上,在顶点处取最小值,当d=2时,的最小值是4,
∴当d=2时,DC有最小值为,
由两点间距离公式得OC=,
∴有最小值为,
∴的最小值为;
(3)解:∵,
∴,
∵,
∴,
∵OC=2,
∴B=AB=1,
∴点B的坐标是(3,0),
设直线BC的解析式为y=x+,
把点B(3,0),C(2,﹣2)代入得,
解得,
∴直线BC的解析式为y=2x-6,
设点的坐标是(p,q),
∴线段A的中点为(,),
由折叠的性质知点(,)在直线BC上,
∴=2×-6,
解得q=2p-4,
由两点间距离公式得B=,
整理得=1,
解得p=2或p=,
当p=2时,q=2p-4=0,此时点(2,0),很显然不符合题意,
当p=时,q=2p-4=,此时点(,),符合题意,
设直线的解析式为y=x+,
把点B(3,0),(,)代入得,,
解得,
∴直线的解析式为y=x+4,
联立直线和抛物线得到,,
解得,,
∴直线与二次函数的交点横坐标为或.
23.【答案】(1)证明:如图中,
∵,
,
在和中,
,
≌,
;
(2)解:如图中,
,
∽,
∴,
可以假设,
∵
∴
,∴
解得,(负根已经舍去),
∴
∵
∴;
(3)解:如图中,,
将绕点A逆时针旋转得到,连接,则,
∵
∴
∵
∴
∴∽,
∴
∵
∴
∵
∴
∴
∴
2 / 2
考试时间:100分钟 满分:120分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 三分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个正确的。
得分
1.一个数x的相反数的绝对值为3,则这个数是( )
A.3 B.﹣3 C.|﹣x| D.±3
2.无锡地铁2号线已开工,全长约33200m,将33200用科学记数法表示应为( )
A.0.332×105 B.3.32×104 C.33.2×103 D.332×102
3.如图是某几何体得三视图,则这个几何体是( )
A.球 B.圆锥 C.圆柱 D.三棱体
4.下列运算正确的是( )
A.a2 a3=a6 B.(a2)3=a5 C.(2a)2=4a2 D.3a2÷a2=3a
5.如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.若不等式组无解,则的取值范围是( )
A. B. C.m≥2 D.m≤2
7.若关于x的一元二次方程 有两个实数根,则m的取值范围为( )
A. B. 且
C. D. 且
8.学校团委在“五四”青年节举行“校园之星”颁奖活动中,九(1)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则所选两名代表恰好是甲和乙的概率是( )
A. B. C. D.
9.不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
10.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后停车卸货刚好一个小时,然后沿原路返回,且往返速度的大小不变,两车离甲地的距离(单位:)与慢车行驶时间(单位:)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A. B. C. D.
阅卷人 二、填空题(每小题3分,共15分)
得分
11.如果中午12:00记作0小时,午后3点钟记作+3小时,那么上午10点钟可表示为 小时.
12.如图,内接于于点H,若,的半径为7,则AB= .
13.已知样本x1,x2,x3,…,x2014的方差是2,那么样本3x1-1,3x2-1,3x3-1,…,3x2014-1的方差是 .
14.如图是一个正六边形的飞镖游戏板,顺次连接三个不相邻的顶点将正六边形分成4个区域。向该游戏板投掷飞镖一次(假设飞镖落在游戏板上,且落在游戏板上的位置是随机的),则飞镖落在阴影区域的概率是 .
15.如图,在矩形中,,,点,分别在边,上,且,按以下步骤操作:
第一步,沿直线翻折,点的对应点恰好落在对角线上,点的对应点为,则 ;
第二步,分别在,上取点,,沿直线继续翻折,使点与点重合,则线段的长为 .
阅卷人 三、解答题(本大题共8个小题,共75分)
得分
16.计算:
(1)
(2)
17.近日,据农业农村部消息,“红火蚁”已传播至我国12个省份,435个县市区,经常出现在路边、草地、公园……其危害性极大.国家九部门联合部署防控行动,紧急防控红火蚁.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
请你根据上面的信息,解答下列问题
(1)本次共调查了 名员工,条形统计图中m= ;
(2)若该公司共有员工1000名,请你估计不了解防护措施的人数= 名;
(3)在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若
从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
18.如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)
19.某百货商店服装柜在销售中发现:某品牌童装每天可售出20件,每件盈利40元,经市场调查发现,在进货价不变的情况下,若每件童装每降价1元,日销售量将增加2件.
(1)当每件童装降价多少元时,一天的盈利最多?
(2)若商场要求一天的盈利为1200元,同时又使顾客得到实惠,每件童装降价多少元?
20.某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系书和自变量x的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
21.综合与探究
如图,抛物线 ,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴为l.
(1)求点A,B,C的坐标;
(2)若点D是第一象限内抛物线上一点,过点D作 轴于点E,交直线BC于点F,当 时,求四边形DOBF的面积;
(3)在(2)的条件下,若点M在抛物线上,点N在抛物线的对称轴上,是否存在以点B,D,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
22.如图,二次函数与轴交于 (0,0), (4,0)两点,顶点为,连接、,若点是线段上一动点,连接,将沿折叠后,点落在点的位置,线段与轴交于点,且点与、点不重合.
(1)求二次函数的表达式;
(2)①求证:;
②求;
(3)当时,求直线与二次函数的交点横坐标.
23.如图
【证明体验】
(1)如图①,在和中,,,,连接,.
求证:;
(2)【思考探究】如图②,在①的条件下,若,,,,求的长;
(3)【拓展延伸】如图③,在四边形中,,,,,,求的值.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】-2
12.【答案】
13.【答案】2
14.【答案】
15.【答案】2;
16.【答案】(1)解:
=3
(2)解:
=5
17.【答案】(1)60;20
(2)200
(3)解:根据题意,列表如下:
第1名 第2名
女
女
由上表可知,共有12种结果,每种结果出现的可能性都相等,其中恰好抽中一男一女的结果有6种,
故所求概率为 .
18.【答案】解:如图,延长FH,交CD于点M,交AB于点N,
∵ ∠BHN=45°,BA⊥MH,
则BN=NH,
设BN=NH=x,
∵ HF=6,∠BFN=30°,且tan∠BFN= = ,
∴tan30°= ,
解得x≈8.22,
根据题意可知:
DM=MH=MN+NH,
∵ MN=AC=10,
则DM=10+8.22=18.22,
∴ CD=DM+MC=DM+EF=18.22+1.6=19.82≈19.8(m).
答:建筑物CD的高度约为19.8m.
19.【答案】(1)解:设每件童装降价x元,则每天盈利为S,
则S=(40﹣x)(2x+20)=﹣2x2+60x+800,
当x==15时,S有最大值为1250元;
(2)解:一天盈利为1200元,则
S=﹣2x2+60x+800=1200,
整理得:﹣2x2+60x﹣400=0,
a=﹣2,b=60,c=﹣400,
b2﹣4ac=3600﹣(4×2×400)=400>0,
解得:x1=20,x2=10,(舍去)
∴每件童装降价20元.
20.【答案】(1)解:根据题意,得:y=60+10x,
由36﹣x≥24得x≤12,
∴1≤x≤12,且x为整数
(2)解:设所获利润为W,
则W=(36﹣x﹣24)(10x+60)
=﹣10x2+60x+720
=﹣10(x﹣3)2+810,
∴当x=3时,W取得最大值,最大值为810,
答:超市定价为33元时,才能使每月销售牛奶的利润最大,最大利润是810元
21.【答案】(1)解:由 ,得 .
解方程,得 , .
∵点A在点B的左侧,∴点A的坐标为(-2,0),点B的坐标为(4,0).
由 ,得 ,∴点C的坐标为(0,-2)
(2)解:设直线BC的函数表达式为 ,经过点B(4,0),C(0,-2),∴ 解得 ,∴直线BC的函数表达式为 .
设点D的坐标为 ,则点F的坐标为 ,点E的坐标为(m,0).
∵点D在第一象限,∴ .
又∵ ,∴ .
解得 , (舍去),∴点E的坐标为(5,0),点D的坐标为 ,点F的坐标为 ,∴ .
(3)解:设点N的坐标为(1,n),
①当NB为对角线时,如答图1所示,
点M的坐标为 .
代入 ,得 ,解得 .
此时点M的坐标为(0,-2);
②当ND为对角线时,如答图2所示,
点M的坐标为 ,
代入 ,得 .
解得 .
此时点M的坐标为(2,-2);
③当BD为对角线时,如答图3所示,
点M的坐标为 ,
代入 ,得 .
解得 .
此时点M的坐标为(8,10).
综上所述:存在以点B,D,M,N为顶点的四边形是平行四边形,点M的坐标分别为(0,-2)或(2,-2)或(8,10).
22.【答案】(1)解:∵二次函数与轴交于 (0,0), (4,0)两点,
∴代入 (0,0), (4,0)得,,
解得:,
∴二次函数的表达式为;
(2)解:①证明:∵=,
∴顶点C的坐标是(2,﹣2),抛物线的对称轴为直线x=2,
∵二次函数与轴交于(0,0),(4,0)两点,
∴由抛物线的对称性可知OC=AC,
∴∠CAB=∠COD,
∵沿折叠后,点落在点的位置,线段与轴交于点,
∴ △ABC≌△BC,
∴∠CAB=∠,AB=B,
∴∠COD=∠,
∵∠ODC=∠BD,
∴;
②∵,
∴,
设点D的坐标为(d,0),
由两点间距离公式得DC=,
∵点与、点不重合,
∴0<d<4,
对于 =来说,
∵ a=1>0,
∴抛物线开口向上,在顶点处取最小值,当d=2时,的最小值是4,
∴当d=2时,DC有最小值为,
由两点间距离公式得OC=,
∴有最小值为,
∴的最小值为;
(3)解:∵,
∴,
∵,
∴,
∵OC=2,
∴B=AB=1,
∴点B的坐标是(3,0),
设直线BC的解析式为y=x+,
把点B(3,0),C(2,﹣2)代入得,
解得,
∴直线BC的解析式为y=2x-6,
设点的坐标是(p,q),
∴线段A的中点为(,),
由折叠的性质知点(,)在直线BC上,
∴=2×-6,
解得q=2p-4,
由两点间距离公式得B=,
整理得=1,
解得p=2或p=,
当p=2时,q=2p-4=0,此时点(2,0),很显然不符合题意,
当p=时,q=2p-4=,此时点(,),符合题意,
设直线的解析式为y=x+,
把点B(3,0),(,)代入得,,
解得,
∴直线的解析式为y=x+4,
联立直线和抛物线得到,,
解得,,
∴直线与二次函数的交点横坐标为或.
23.【答案】(1)证明:如图中,
∵,
,
在和中,
,
≌,
;
(2)解:如图中,
,
∽,
∴,
可以假设,
∵
∴
,∴
解得,(负根已经舍去),
∴
∵
∴;
(3)解:如图中,,
将绕点A逆时针旋转得到,连接,则,
∵
∴
∵
∴
∴∽,
∴
∵
∴
∵
∴
∴
∴
2 / 2
同课章节目录
