六年级下册数学青岛版圆柱的表面积 课件(共32张PPT)
文档属性
| 名称 | 六年级下册数学青岛版圆柱的表面积 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 576.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 20:54:11 | ||
图片预览








文档简介
(共32张PPT)
青岛版六年级数学下册
圆柱的表面积
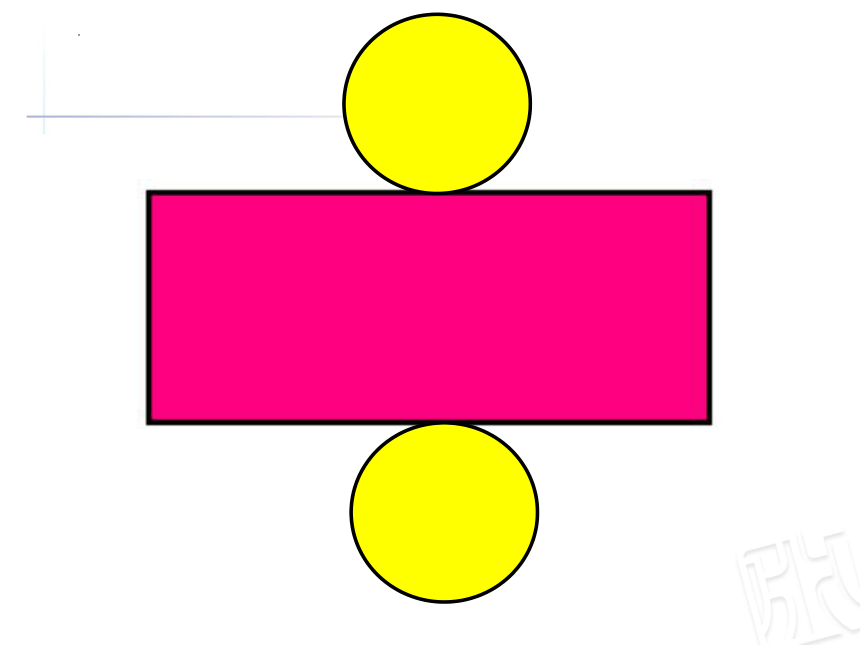
从图中,你知道了哪些数学信息?
底面直径2dm,高3dm。
做一个这样的圆柱形纸筒,至少需要多少纸板?
根据这些信息,你能提出哪些问题?
一、创设情境,提出问题
求需要多少纸板,也就是求圆柱形纸筒的表面积。
做一个这样的圆柱形纸筒,至少需要多少纸板
怎样求圆柱的表面积呢
圆柱的侧面积加上两个底面积就是圆柱的表面积。
探究提示:
(1)拆开圆柱体纸盒,观察它的结构,表面积由几部分组成?
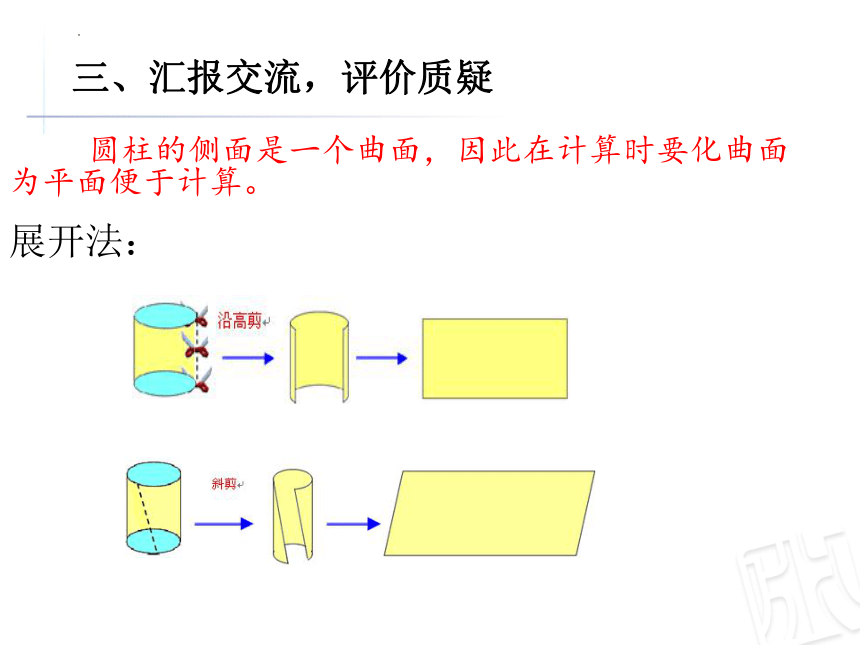
(2)圆柱的侧面是什么形?想一想,能否将其转化成我们学过的平面图形?观察二者之间的对应关系。
(3)计算出圆柱纸板的表面积。
(4)你能说出圆柱的表面积的计算公式吗?和同伴交流一下。
二、自主学习,小组探究
三、汇报交流,评价质疑
圆柱的侧面是一个曲面,因此在计算时要化曲面为平面便于计算。
展开法:
大家想一想,我们还能想出哪些方法,也可以把曲面转化成平面呢?
滚动法:
围成法:
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面的周长
底面
高
底面
底面
底面
底面的周长
高
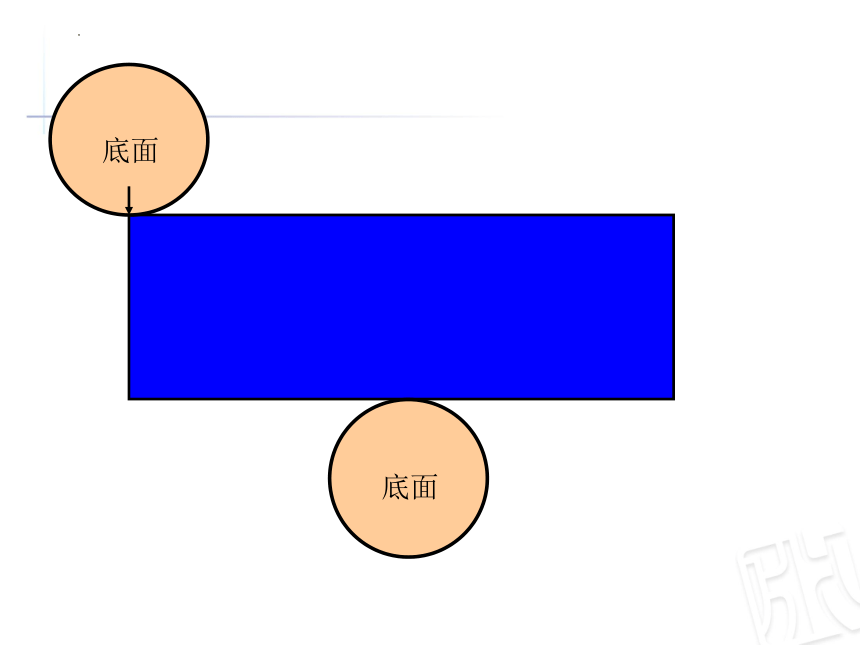
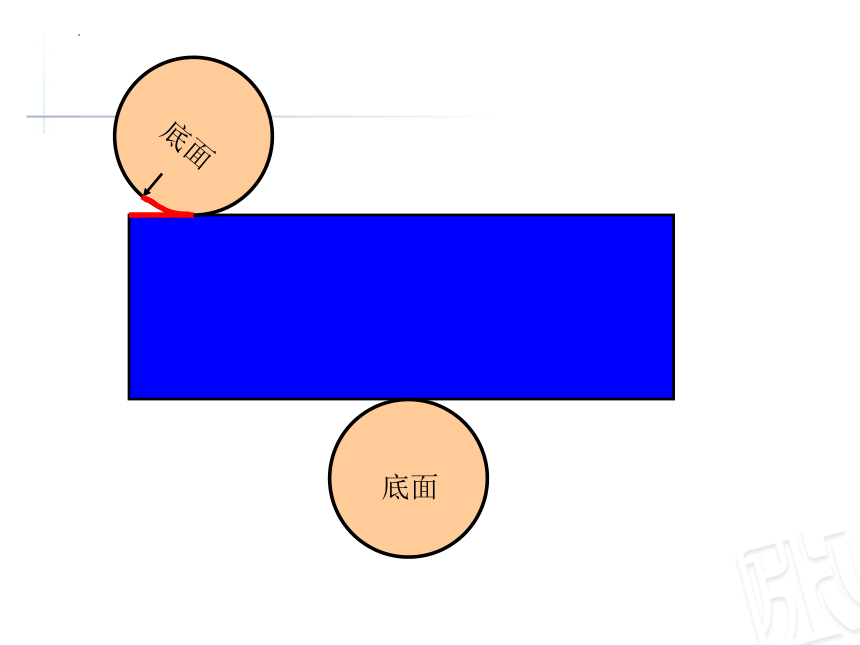
长方形纸的长等于圆柱底面的周长。
长方形纸的宽等于圆柱的高。
侧面积的求法
我知道:用圆柱底面的周长乘以高
你知道侧面积怎么计算了吗?
如果用S表示圆柱的侧面积,C表示底面周长,h表示高,S侧=Ch
侧面积
圆柱的侧面积加上两个底面的面积就是圆柱的表面积。即:
怎样计算圆柱的表面积?
你能求出圆柱纸筒的表面积吗
底面积:
侧面积:
18.84 + 3.14×2 =25.12(平方分米)
表面积 = 侧面积 + 底面积 × 2
3.14×2×3 =18.84(平方分米)
3.14×(2÷2) =3.14(平方分米)
答:做一个这样的圆柱形纸筒,至少需要25.12平方分米的纸板。
⑴已知底面周长和高如何计算它的侧面积?
⑵已知圆柱底面直径和高如何计算它的侧面积?
⑶已知圆柱底面半径和高如何计算它的侧面积?
S侧=Ch
S侧=πdh
S侧=2πrh
四、抽象概括,总结提升
1.计算下面圆柱的侧面积和表面积。(单位:dm)
侧面积:3.14×2×5×10 = 314(平方分米)
底面积:3.14×5×5=78.5(平方分米)
表面积:2×78.5+314=471(平方分米)
五、巩固训练,拓展提高
1.计算下面圆柱的侧面积和表面积。(单位:dm)
侧面积: 3.14×2×4.5
= 28.26(平方分米)
底面积: 3.14×(2÷2)2
= 3.14(平方分米)
表面积: 2 ×3.14 + 28.26
= 34.54(平方分米)
2. 如右图,制作这样一个饮料罐至少需要多少铁皮?这个饮料罐的商标纸需要多少平方厘米? (得数保留整数)
温馨提示:
①说一说,求制作这样一个饮料罐至少需要多少铁皮?其实就是求什么呢?
②想一想,“得数保留整十平方厘米”能用“四舍五入法” 吗?
计算圆柱形物体的表面积要注意以下几种情况:
●求侧面积。只有侧面而无底面的圆柱状物体。如:烟囱、铅笔或木桩涂漆的部分、压路机滚筒、罐头盒商标纸等等。
●一个侧面加一个底面。如:圆柱状笔筒、玻璃杯、圆柱无盖水桶等。
●一个侧面加两个底面。如:圆柱状茶叶桶、罐头盒、汽油桶、中药盒等。
3.一台压路机的前轮是圆柱形,轮宽1.5米,直径为1.2米。
(1)前轮滚动一周,压过的路面是多少平方米?(得数保留两位小数)
(2)如果每分钟滚动15周,压过的路面是多少平方米?
(1)3.14×1.2×1.5≈5.65(平方米)
(2)5.652×15=84.78(平方米)
答:压过的路面约是5.65平方米。
答:压过的路面是84.78平方米。
底面
底面
底面的周长
高
圆柱的表面积=圆柱的侧面积+两个底面的面积
知识回顾
=
表面积
底面积
+
侧面积
+
底面积
青岛版六年级数学下册
圆柱的表面积
从图中,你知道了哪些数学信息?
底面直径2dm,高3dm。
做一个这样的圆柱形纸筒,至少需要多少纸板?
根据这些信息,你能提出哪些问题?
一、创设情境,提出问题
求需要多少纸板,也就是求圆柱形纸筒的表面积。
做一个这样的圆柱形纸筒,至少需要多少纸板
怎样求圆柱的表面积呢
圆柱的侧面积加上两个底面积就是圆柱的表面积。
探究提示:
(1)拆开圆柱体纸盒,观察它的结构,表面积由几部分组成?
(2)圆柱的侧面是什么形?想一想,能否将其转化成我们学过的平面图形?观察二者之间的对应关系。
(3)计算出圆柱纸板的表面积。
(4)你能说出圆柱的表面积的计算公式吗?和同伴交流一下。
二、自主学习,小组探究
三、汇报交流,评价质疑
圆柱的侧面是一个曲面,因此在计算时要化曲面为平面便于计算。
展开法:
大家想一想,我们还能想出哪些方法,也可以把曲面转化成平面呢?
滚动法:
围成法:
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面的周长
底面
高
底面
底面
底面
底面的周长
高
长方形纸的长等于圆柱底面的周长。
长方形纸的宽等于圆柱的高。
侧面积的求法
我知道:用圆柱底面的周长乘以高
你知道侧面积怎么计算了吗?
如果用S表示圆柱的侧面积,C表示底面周长,h表示高,S侧=Ch
侧面积
圆柱的侧面积加上两个底面的面积就是圆柱的表面积。即:
怎样计算圆柱的表面积?
你能求出圆柱纸筒的表面积吗
底面积:
侧面积:
18.84 + 3.14×2 =25.12(平方分米)
表面积 = 侧面积 + 底面积 × 2
3.14×2×3 =18.84(平方分米)
3.14×(2÷2) =3.14(平方分米)
答:做一个这样的圆柱形纸筒,至少需要25.12平方分米的纸板。
⑴已知底面周长和高如何计算它的侧面积?
⑵已知圆柱底面直径和高如何计算它的侧面积?
⑶已知圆柱底面半径和高如何计算它的侧面积?
S侧=Ch
S侧=πdh
S侧=2πrh
四、抽象概括,总结提升
1.计算下面圆柱的侧面积和表面积。(单位:dm)
侧面积:3.14×2×5×10 = 314(平方分米)
底面积:3.14×5×5=78.5(平方分米)
表面积:2×78.5+314=471(平方分米)
五、巩固训练,拓展提高
1.计算下面圆柱的侧面积和表面积。(单位:dm)
侧面积: 3.14×2×4.5
= 28.26(平方分米)
底面积: 3.14×(2÷2)2
= 3.14(平方分米)
表面积: 2 ×3.14 + 28.26
= 34.54(平方分米)
2. 如右图,制作这样一个饮料罐至少需要多少铁皮?这个饮料罐的商标纸需要多少平方厘米? (得数保留整数)
温馨提示:
①说一说,求制作这样一个饮料罐至少需要多少铁皮?其实就是求什么呢?
②想一想,“得数保留整十平方厘米”能用“四舍五入法” 吗?
计算圆柱形物体的表面积要注意以下几种情况:
●求侧面积。只有侧面而无底面的圆柱状物体。如:烟囱、铅笔或木桩涂漆的部分、压路机滚筒、罐头盒商标纸等等。
●一个侧面加一个底面。如:圆柱状笔筒、玻璃杯、圆柱无盖水桶等。
●一个侧面加两个底面。如:圆柱状茶叶桶、罐头盒、汽油桶、中药盒等。
3.一台压路机的前轮是圆柱形,轮宽1.5米,直径为1.2米。
(1)前轮滚动一周,压过的路面是多少平方米?(得数保留两位小数)
(2)如果每分钟滚动15周,压过的路面是多少平方米?
(1)3.14×1.2×1.5≈5.65(平方米)
(2)5.652×15=84.78(平方米)
答:压过的路面约是5.65平方米。
答:压过的路面是84.78平方米。
底面
底面
底面的周长
高
圆柱的表面积=圆柱的侧面积+两个底面的面积
知识回顾
=
表面积
底面积
+
侧面积
+
底面积
