北师大版五年级下册数学二 长方体(一)展开与折叠作业(含解析)
文档属性
| 名称 | 北师大版五年级下册数学二 长方体(一)展开与折叠作业(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 23:03:13 | ||
图片预览




文档简介
小学数学北师大版五下展开与折叠作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个正方体的平面展开图如图所示,则原正方体中与“数”所在面相对的面所标的字是( )。
A.好 B.有 C.趣
2.如图是一个正方体的平面展开图,与汉字“塞”相对面上的汉字是( )。
A.榆 B.林 C.明 D.珠
3.下面四个图形中,不能折叠成正方体的是( )。
A. B. C. D.
4.折一折,用 做一个,“道”的对面是( )。
A.教 B.贵 C.以
5.下面图形沿虚线折叠不能围成正方体的是( )。
A. B. C. D.
6.由图折叠而成的立方体是( )。
A. B. C.
7.下边图形的展开图,不正确的是( )。
A. B. C. D.
8.的展开图是( )。
A. B. C. D.
9.长方体的6个面展开后,( )。
A.都是长方形 B.至少有2个面是长方形
C.至少有4个面是长方形 D.都是正方形
10.下面展开图中,能围成正方体或长方体的是( )。
A. B. C. D.
11.下面盒子的展开图是( )。
A. B. C. D.
12.下列图形沿虚线折叠后不能围成长方体的是( )。
A. B. C. D.
二、填空题
13.把一个正方体盒子沿着棱剪开,得到一个展开图,如图。
你也剪一剪,会得到怎样的展开图?与同学交流。再将一个长方体盒子沿棱剪开,试试看。
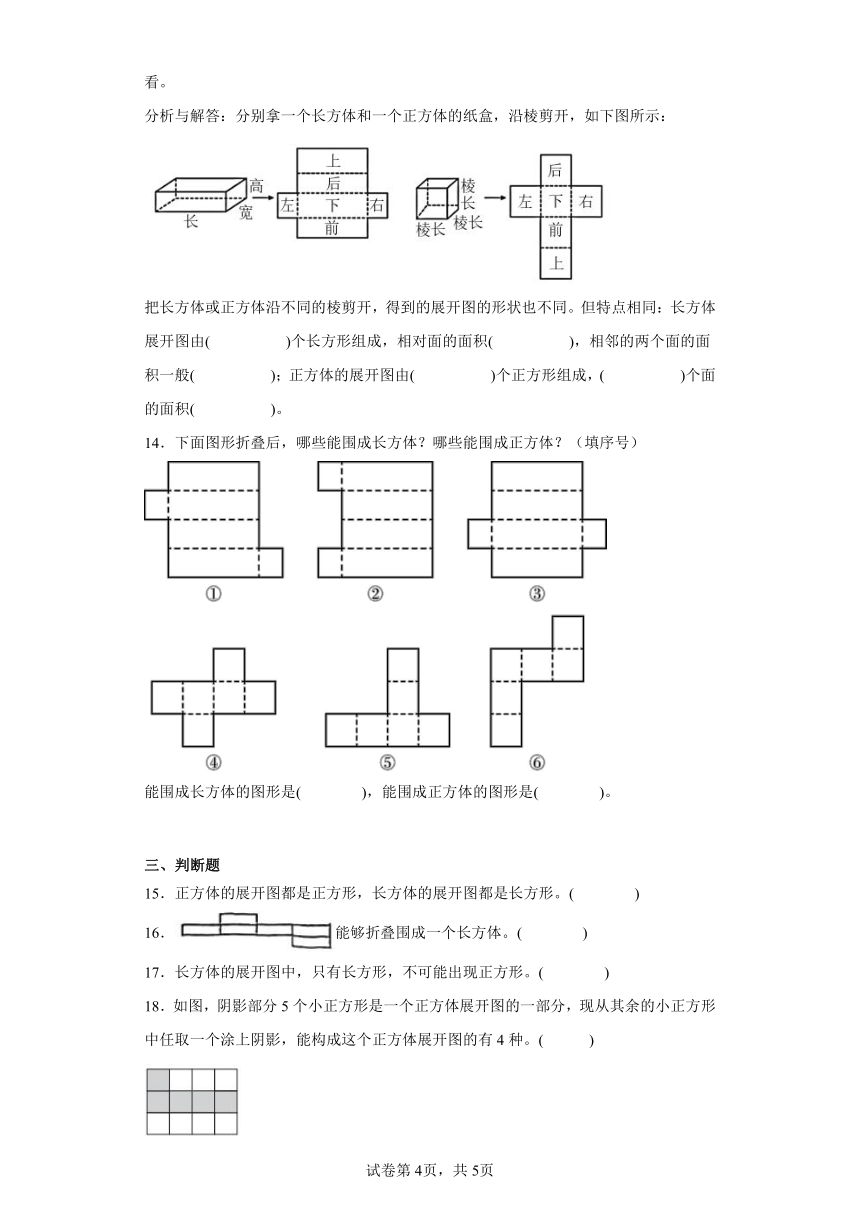
分析与解答:分别拿一个长方体和一个正方体的纸盒,沿棱剪开,如下图所示:
把长方体或正方体沿不同的棱剪开,得到的展开图的形状也不同。但特点相同:长方体展开图由( )个长方形组成,相对面的面积( ),相邻的两个面的面积一般( );正方体的展开图由( )个正方形组成,( )个面的面积( )。
14.下面图形折叠后,哪些能围成长方体?哪些能围成正方体?(填序号)
能围成长方体的图形是( ),能围成正方体的图形是( )。
三、判断题
15.正方体的展开图都是正方形,长方体的展开图都是长方形。( )
16.能够折叠围成一个长方体。( )
17.长方体的展开图中,只有长方形,不可能出现正方形。( )
18.如图,阴影部分5个小正方形是一个正方体展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体展开图的有4种。( )
四、解答题
19.熊妈妈在魔方的六个面上各贴了一个数字,分别是1,2,3,4,5,6。第一次熊宝宝看到了,第二次熊宝宝又看到了。数字1,2,3对面分别是多少?
20.在下面方格图(每个小正方形边长均为1厘米)上补全这个长方体展开图的上面、右面和后面,并填空。
上图长方体的长( )厘米,宽( )厘米,高( )厘米。
21.宣纸质地柔软,经久耐用,被称为“千年寿纸”。陈师傅将宣纸裁成了如图A的形状,艺术创作后,准备加上木条制作成如图B所示的长方体灯罩,要做出这样一个灯罩,至少需要多少厘米的木条?
22.如图,一张硬纸板剪下4个边长4厘米的小正方形后,可以做成一个没有盖子的盒子。请你求出剪后的硬纸板的面积?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的"1-3-2"型,折成正方体后,“数”与“有”相对,“学”与“玩”相对,“好”与“趣”相对,据此解答。
【详解】由分析可得:一个正方体的平面展开图如图所示,则原正方体中与“数”所在面相对的面所标的字是有。
故答案为:B
2.C
【分析】此图属于正方体展开图的“1-4-1”型,“1-4-1”型需要中间4个一连串,两边各一随便放,也就是一个的正方形需要在4个的正方形两边,不能同时出现在一边;
相对的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,“z”字两端处的小正方形是正方体的对面,据此答题即可。
【详解】由分析可得:
如图:折成正方体后,“榆”与“林”相对,“塞”与“明”相对,“上”与“珠”相对。
故答案为:C
【点睛】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,掌握规律是解答本题的关键。
3.B
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:
(1)一条线上不过四;
(2)“田字形”“七字型”“凹字型”;据此解答。
【详解】由分析可知:
A.属于“2—3—1”型,能折叠成正方体;
B.不属于正方体的展开图类型,不能折叠成正方体,折叠时有重叠的面;
C.属于“2—3—1”型,能折叠成正方体;
D.属于“1—4—1”型,能折叠成正方体。
故答案为:B
【点睛】本题考查正方体展开图。有11种情况,分四种类型: “1-4-1”结构、“2-2-2”结构、“3-3”结构和“2-3-1”结构。
4.C
【分析】根据正方体的特征可知,正方体展开后,相对的两个面中间会隔着一个正方形。
所以,“之”的对面是“贵”,“道”的对面是“以”,“教”的对面是“专”;据此解决。
【详解】由题意分析得:
用做一个,“道”的对面是“以”。
故答案为:C
【点睛】此题主要考查的是正方体的展开与折叠,要熟记图形的特征。
5.C
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:
(1)一条线上不过四;
(2)“田字形”“七字型”“凹字型”;据此解答。
【详解】A. 属于“2—2—2”型,可以围成;
B. 属于“2—3—1”型。可以围成;
C. 属于“七字型”,有一个面没有被围起来,所以不能围成;
D. 属于“1—4—1”型,可以围成;
故答案为:C。
【点睛】本题考查正方体展开图。有11种情况,分四种类型: “1-4-1”结构、“2-2-2”结构、“3-3”结和“1-3-2”结构。
6.C
【分析】根据正方体展开图的特点可知,黑色的圆和三角形是相对的面,那么拼成的正方体黑色的圆和三角形不可能相邻,据此即可选择。
【详解】由分析可知:A、B两个正方体黑色的圆和三角形相邻,不符合题意。
故答案为:C
【点睛】本题主要考查正方体的展开图,可以动手去折一下。
7.C
【分析】观察图形,可知这是一个特殊的长方体,有2个相对的面是正方形,有4个完全相同的长方形;沿着长方体的一些棱剪开,可以得到长方体的展开图,在展开图中,长方体相对的面完全相同;据此分析即可。
【详解】据上分析可知:A、B、D三个选项的展开图是正确的,而C选项中有4个正方形面,是不正确的。
故答案为:C
【点睛】此题重点考查对长方体特征的认识和展开图的识别。
8.C
【分析】根据图示可知,盒子的四个侧面是4个三角形,据此分析解答即可。
【详解】根据图示可知,盒子的四个侧面是4个三角形,所以盒子的展开图是C选项。
故答案为:C
【点睛】本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键。
9.C
【分析】一般情况下,长方体的6个面展开后,都是长方形;在特殊情况下,长方体的6个面展开有两个是正方形,其它4个面是完全相同的长方形;据此解答即可。
【详解】由分析得:长方体的6个面展开后,至少有4个面是长方形。
故答案为:C
【点睛】本题主要考查长方体的展开图,明确正方体是特殊的长方体是解答本题的关键。
10.C
【分析】根据长方体、正方体展开图的特征,对照选项去判断每种图形即可。
【详解】A .该图不符合长方体或正方体的展开特征;
B.该图不符合长方体或正方体的展开特征;
C.符合正方体的展开图的“一四一”型,是正方体的展开图;
D.该图是三棱柱的展开图,不是正方体或长方体的展开图。
故答案为:C
【点睛】此题主要考查长方体、正方体展开图的掌握及应用,具有较强的空间想象能力。
11.B
【分析】观察立体图可知,图形盒子四个侧面是4个等腰梯形组成,上底面四边形比下底面四边形要小,展开后,上面的边和下面的边有些成弧形,由此进行判断。
【详解】根据分析可知,盒子展开后的图形是。
故答案为:B
【点睛】本题考查立体图形的展开图,根据盒子的特点,进行解答。
12.B
【分析】根据长方体的展开图以及长方体的特征进行逐一判断。
【详解】A.,符合长方体展开图的“1-4-1”型结构,折叠后能围成长方体;
B.,不符合长方体展开图的特征,折叠后不能围成长方体;
C.,符合长方体展开的的“1-4-1”型结构,折叠后能围成长方体;
D.,符合长方体展开图的“1-4-1”型结构,折叠后能围成长方体。
故答案为:B
【点睛】本题考查长方体展开图的特征,关键是熟记长方体展开图的特征。
13. 6 相等 不相等 6 6 相等
【分析】长方体和正方体都是由6个面组成的,剪开后仍是6个面。长方体相对的面的面积相等,正方体的每个面面积都相等。据此解题。
【详解】把长方体或正方体沿不同的棱剪开,得到的展开图的形状也不同。但特点相同:长方体展开图由6个长方形组成,相对面的面积相等,相邻的两个面的面积一般不相等;正方体的展开图由6个正方形组成,6个面的面积相等。
【点睛】本题考查了长方体和正方体的展开图,掌握长方体和正方体的特征是解题的关键。
14. ①③ ④
【分析】如果把一个正方体或长方体盒子沿着棱剪开,平铺成一个平面图形,就形成了它们的展开图,这些展开图也存在一定的规律,违背了规律是不能折成立体图形的。
【详解】①可以围成长方体;
②不能围成立体图形,在围的时候,会有两个底面重叠;
③可以围成长方体;
④可以围成正方体,
⑤不能围成立体图形,假设底下一排4个小正方形围成侧面,上面2个小正方形落下来,会与刚才围成的侧面相重叠;
⑥这是典型的“7”字型展开图,是围不成正方体的。
【点睛】综合了长方体、正方体的展开图,不仅需要我们熟悉这两种立体图形的特征,也需要我们善于总结展开图的一些规律。
15.×
【分析】长方体的每个面都是长方形(特殊情况下有2个正方形的面),相对的面完全相同;正方体的每个面都是正方形,每一面完全相同,据此解答。
【详解】根据分析可知,正方体展开图都是正方形,长方体展开图的在特殊的情况下有2个面是正方形。
原题干说法错误。
故答案为:×
【点睛】熟练掌握长方体、正方体的体征以及展开图的特征进行解答。
16.×
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等,相对的四条棱长度相等;据此解答。
【详解】根据长方体的特征可知,上下两个长方形的宽较短,不符合长方体的特征,所以不能围成一个长方体。
不能折叠成一个长方体。
原题干说法错误。
故答案为:×
【点睛】熟练掌握长方体的特征是解答本题的关键。
17.×
【分析】长方体有6个面,其中有两个相对的面可能是正方形,据此解答。
【详解】当长方体有两个相对的面是正方形时,它的展开图中会有两个正方形。原题说法错误。
故答案为:×
【点睛】掌握特殊的长方体的特征是解题的关键。
18.√
【分析】由平面图形的折叠及正方体的展开图解题。
【详解】能构成这个正方体的表面展开图的有:
故答案为:√
【点睛】考查了几何体的展开图,解题时勿忘记正方体展开图的各种情形。
19.见详解
【分析】从两次的图形中可以得知:3是和1、2、4、6相邻,所以3的对面就是5;由第二次看到的图形可以得知2与1、3、5、6相邻,据此可推出2的对面是4,进而推出1的对面是6。据此解答。
【详解】根据分析可得,以3为中心的展开图如下:
答:数字1的对面是数字6;数字2的对面是数字4;数字3的对面是数字5。
【点睛】本题的关键是明确数字6是靠着数字2的。
20.画图见详解;5;4;2
【分析】根据长方体的特征,长方体的上面和下面完全相同,左面和右面完全相同,前面和后面完全相同,据此画图即可;由上图可数出长方体的长为5格,即5厘米,宽为4格,即4厘米,高为2格,即2厘米。
【详解】如下如:
长是5厘米,宽是4厘米,高是2厘米。
【点睛】本题考查长方体的特征以及长方体的展开图,学生需熟练掌握长方体的基本特征。
21.280厘米
【分析】根据题意可知,灯罩的长36厘米、宽12厘米、高22厘米,根据长方体的棱长和公式:长方体棱长和=(长+宽+高)×4,代入数据解答,即可求出至少需要多少厘米的木条。
【详解】(36+22+12)×4
=70×4
=280(厘米)
答:至少需要280厘米的木条。
【点睛】本题主要考查了长方体棱长和公式的灵活应用,要熟练掌握公式。
22.456平方厘米
【分析】由题意可知,剪后的硬纸板的面积=原长方形面积-4×小正方形面积,将数值代入长方形面积计算公式求值即可。
【详解】26×20-4×4×4
=520-64
=456(cm2)
答:剪后的硬纸板的面积是456平方厘米。
【点睛】此题主要考查了学生动手操作的能力,在计算不规则图形的面积时,一般都会把它转化成几个规则图形的面积之和或差,再利用规则图形的面积公式进行解答。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个正方体的平面展开图如图所示,则原正方体中与“数”所在面相对的面所标的字是( )。
A.好 B.有 C.趣
2.如图是一个正方体的平面展开图,与汉字“塞”相对面上的汉字是( )。
A.榆 B.林 C.明 D.珠
3.下面四个图形中,不能折叠成正方体的是( )。
A. B. C. D.
4.折一折,用 做一个,“道”的对面是( )。
A.教 B.贵 C.以
5.下面图形沿虚线折叠不能围成正方体的是( )。
A. B. C. D.
6.由图折叠而成的立方体是( )。
A. B. C.
7.下边图形的展开图,不正确的是( )。
A. B. C. D.
8.的展开图是( )。
A. B. C. D.
9.长方体的6个面展开后,( )。
A.都是长方形 B.至少有2个面是长方形
C.至少有4个面是长方形 D.都是正方形
10.下面展开图中,能围成正方体或长方体的是( )。
A. B. C. D.
11.下面盒子的展开图是( )。
A. B. C. D.
12.下列图形沿虚线折叠后不能围成长方体的是( )。
A. B. C. D.
二、填空题
13.把一个正方体盒子沿着棱剪开,得到一个展开图,如图。
你也剪一剪,会得到怎样的展开图?与同学交流。再将一个长方体盒子沿棱剪开,试试看。
分析与解答:分别拿一个长方体和一个正方体的纸盒,沿棱剪开,如下图所示:
把长方体或正方体沿不同的棱剪开,得到的展开图的形状也不同。但特点相同:长方体展开图由( )个长方形组成,相对面的面积( ),相邻的两个面的面积一般( );正方体的展开图由( )个正方形组成,( )个面的面积( )。
14.下面图形折叠后,哪些能围成长方体?哪些能围成正方体?(填序号)
能围成长方体的图形是( ),能围成正方体的图形是( )。
三、判断题
15.正方体的展开图都是正方形,长方体的展开图都是长方形。( )
16.能够折叠围成一个长方体。( )
17.长方体的展开图中,只有长方形,不可能出现正方形。( )
18.如图,阴影部分5个小正方形是一个正方体展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体展开图的有4种。( )
四、解答题
19.熊妈妈在魔方的六个面上各贴了一个数字,分别是1,2,3,4,5,6。第一次熊宝宝看到了,第二次熊宝宝又看到了。数字1,2,3对面分别是多少?
20.在下面方格图(每个小正方形边长均为1厘米)上补全这个长方体展开图的上面、右面和后面,并填空。
上图长方体的长( )厘米,宽( )厘米,高( )厘米。
21.宣纸质地柔软,经久耐用,被称为“千年寿纸”。陈师傅将宣纸裁成了如图A的形状,艺术创作后,准备加上木条制作成如图B所示的长方体灯罩,要做出这样一个灯罩,至少需要多少厘米的木条?
22.如图,一张硬纸板剪下4个边长4厘米的小正方形后,可以做成一个没有盖子的盒子。请你求出剪后的硬纸板的面积?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的"1-3-2"型,折成正方体后,“数”与“有”相对,“学”与“玩”相对,“好”与“趣”相对,据此解答。
【详解】由分析可得:一个正方体的平面展开图如图所示,则原正方体中与“数”所在面相对的面所标的字是有。
故答案为:B
2.C
【分析】此图属于正方体展开图的“1-4-1”型,“1-4-1”型需要中间4个一连串,两边各一随便放,也就是一个的正方形需要在4个的正方形两边,不能同时出现在一边;
相对的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,“z”字两端处的小正方形是正方体的对面,据此答题即可。
【详解】由分析可得:
如图:折成正方体后,“榆”与“林”相对,“塞”与“明”相对,“上”与“珠”相对。
故答案为:C
【点睛】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,掌握规律是解答本题的关键。
3.B
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:
(1)一条线上不过四;
(2)“田字形”“七字型”“凹字型”;据此解答。
【详解】由分析可知:
A.属于“2—3—1”型,能折叠成正方体;
B.不属于正方体的展开图类型,不能折叠成正方体,折叠时有重叠的面;
C.属于“2—3—1”型,能折叠成正方体;
D.属于“1—4—1”型,能折叠成正方体。
故答案为:B
【点睛】本题考查正方体展开图。有11种情况,分四种类型: “1-4-1”结构、“2-2-2”结构、“3-3”结构和“2-3-1”结构。
4.C
【分析】根据正方体的特征可知,正方体展开后,相对的两个面中间会隔着一个正方形。
所以,“之”的对面是“贵”,“道”的对面是“以”,“教”的对面是“专”;据此解决。
【详解】由题意分析得:
用做一个,“道”的对面是“以”。
故答案为:C
【点睛】此题主要考查的是正方体的展开与折叠,要熟记图形的特征。
5.C
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:
(1)一条线上不过四;
(2)“田字形”“七字型”“凹字型”;据此解答。
【详解】A. 属于“2—2—2”型,可以围成;
B. 属于“2—3—1”型。可以围成;
C. 属于“七字型”,有一个面没有被围起来,所以不能围成;
D. 属于“1—4—1”型,可以围成;
故答案为:C。
【点睛】本题考查正方体展开图。有11种情况,分四种类型: “1-4-1”结构、“2-2-2”结构、“3-3”结和“1-3-2”结构。
6.C
【分析】根据正方体展开图的特点可知,黑色的圆和三角形是相对的面,那么拼成的正方体黑色的圆和三角形不可能相邻,据此即可选择。
【详解】由分析可知:A、B两个正方体黑色的圆和三角形相邻,不符合题意。
故答案为:C
【点睛】本题主要考查正方体的展开图,可以动手去折一下。
7.C
【分析】观察图形,可知这是一个特殊的长方体,有2个相对的面是正方形,有4个完全相同的长方形;沿着长方体的一些棱剪开,可以得到长方体的展开图,在展开图中,长方体相对的面完全相同;据此分析即可。
【详解】据上分析可知:A、B、D三个选项的展开图是正确的,而C选项中有4个正方形面,是不正确的。
故答案为:C
【点睛】此题重点考查对长方体特征的认识和展开图的识别。
8.C
【分析】根据图示可知,盒子的四个侧面是4个三角形,据此分析解答即可。
【详解】根据图示可知,盒子的四个侧面是4个三角形,所以盒子的展开图是C选项。
故答案为:C
【点睛】本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键。
9.C
【分析】一般情况下,长方体的6个面展开后,都是长方形;在特殊情况下,长方体的6个面展开有两个是正方形,其它4个面是完全相同的长方形;据此解答即可。
【详解】由分析得:长方体的6个面展开后,至少有4个面是长方形。
故答案为:C
【点睛】本题主要考查长方体的展开图,明确正方体是特殊的长方体是解答本题的关键。
10.C
【分析】根据长方体、正方体展开图的特征,对照选项去判断每种图形即可。
【详解】A .该图不符合长方体或正方体的展开特征;
B.该图不符合长方体或正方体的展开特征;
C.符合正方体的展开图的“一四一”型,是正方体的展开图;
D.该图是三棱柱的展开图,不是正方体或长方体的展开图。
故答案为:C
【点睛】此题主要考查长方体、正方体展开图的掌握及应用,具有较强的空间想象能力。
11.B
【分析】观察立体图可知,图形盒子四个侧面是4个等腰梯形组成,上底面四边形比下底面四边形要小,展开后,上面的边和下面的边有些成弧形,由此进行判断。
【详解】根据分析可知,盒子展开后的图形是。
故答案为:B
【点睛】本题考查立体图形的展开图,根据盒子的特点,进行解答。
12.B
【分析】根据长方体的展开图以及长方体的特征进行逐一判断。
【详解】A.,符合长方体展开图的“1-4-1”型结构,折叠后能围成长方体;
B.,不符合长方体展开图的特征,折叠后不能围成长方体;
C.,符合长方体展开的的“1-4-1”型结构,折叠后能围成长方体;
D.,符合长方体展开图的“1-4-1”型结构,折叠后能围成长方体。
故答案为:B
【点睛】本题考查长方体展开图的特征,关键是熟记长方体展开图的特征。
13. 6 相等 不相等 6 6 相等
【分析】长方体和正方体都是由6个面组成的,剪开后仍是6个面。长方体相对的面的面积相等,正方体的每个面面积都相等。据此解题。
【详解】把长方体或正方体沿不同的棱剪开,得到的展开图的形状也不同。但特点相同:长方体展开图由6个长方形组成,相对面的面积相等,相邻的两个面的面积一般不相等;正方体的展开图由6个正方形组成,6个面的面积相等。
【点睛】本题考查了长方体和正方体的展开图,掌握长方体和正方体的特征是解题的关键。
14. ①③ ④
【分析】如果把一个正方体或长方体盒子沿着棱剪开,平铺成一个平面图形,就形成了它们的展开图,这些展开图也存在一定的规律,违背了规律是不能折成立体图形的。
【详解】①可以围成长方体;
②不能围成立体图形,在围的时候,会有两个底面重叠;
③可以围成长方体;
④可以围成正方体,
⑤不能围成立体图形,假设底下一排4个小正方形围成侧面,上面2个小正方形落下来,会与刚才围成的侧面相重叠;
⑥这是典型的“7”字型展开图,是围不成正方体的。
【点睛】综合了长方体、正方体的展开图,不仅需要我们熟悉这两种立体图形的特征,也需要我们善于总结展开图的一些规律。
15.×
【分析】长方体的每个面都是长方形(特殊情况下有2个正方形的面),相对的面完全相同;正方体的每个面都是正方形,每一面完全相同,据此解答。
【详解】根据分析可知,正方体展开图都是正方形,长方体展开图的在特殊的情况下有2个面是正方形。
原题干说法错误。
故答案为:×
【点睛】熟练掌握长方体、正方体的体征以及展开图的特征进行解答。
16.×
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等,相对的四条棱长度相等;据此解答。
【详解】根据长方体的特征可知,上下两个长方形的宽较短,不符合长方体的特征,所以不能围成一个长方体。
不能折叠成一个长方体。
原题干说法错误。
故答案为:×
【点睛】熟练掌握长方体的特征是解答本题的关键。
17.×
【分析】长方体有6个面,其中有两个相对的面可能是正方形,据此解答。
【详解】当长方体有两个相对的面是正方形时,它的展开图中会有两个正方形。原题说法错误。
故答案为:×
【点睛】掌握特殊的长方体的特征是解题的关键。
18.√
【分析】由平面图形的折叠及正方体的展开图解题。
【详解】能构成这个正方体的表面展开图的有:
故答案为:√
【点睛】考查了几何体的展开图,解题时勿忘记正方体展开图的各种情形。
19.见详解
【分析】从两次的图形中可以得知:3是和1、2、4、6相邻,所以3的对面就是5;由第二次看到的图形可以得知2与1、3、5、6相邻,据此可推出2的对面是4,进而推出1的对面是6。据此解答。
【详解】根据分析可得,以3为中心的展开图如下:
答:数字1的对面是数字6;数字2的对面是数字4;数字3的对面是数字5。
【点睛】本题的关键是明确数字6是靠着数字2的。
20.画图见详解;5;4;2
【分析】根据长方体的特征,长方体的上面和下面完全相同,左面和右面完全相同,前面和后面完全相同,据此画图即可;由上图可数出长方体的长为5格,即5厘米,宽为4格,即4厘米,高为2格,即2厘米。
【详解】如下如:
长是5厘米,宽是4厘米,高是2厘米。
【点睛】本题考查长方体的特征以及长方体的展开图,学生需熟练掌握长方体的基本特征。
21.280厘米
【分析】根据题意可知,灯罩的长36厘米、宽12厘米、高22厘米,根据长方体的棱长和公式:长方体棱长和=(长+宽+高)×4,代入数据解答,即可求出至少需要多少厘米的木条。
【详解】(36+22+12)×4
=70×4
=280(厘米)
答:至少需要280厘米的木条。
【点睛】本题主要考查了长方体棱长和公式的灵活应用,要熟练掌握公式。
22.456平方厘米
【分析】由题意可知,剪后的硬纸板的面积=原长方形面积-4×小正方形面积,将数值代入长方形面积计算公式求值即可。
【详解】26×20-4×4×4
=520-64
=456(cm2)
答:剪后的硬纸板的面积是456平方厘米。
【点睛】此题主要考查了学生动手操作的能力,在计算不规则图形的面积时,一般都会把它转化成几个规则图形的面积之和或差,再利用规则图形的面积公式进行解答。
答案第1页,共2页
答案第1页,共2页
