8.1.2功与功率课件-2023-2024学年高一下学期物理人教版(2019)必修第二册(共29张PPT)
文档属性
| 名称 | 8.1.2功与功率课件-2023-2024学年高一下学期物理人教版(2019)必修第二册(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-12 10:00:45 | ||
图片预览








文档简介
(共29张PPT)
8.1.2 功率
人教版(2019)高中物理必修二
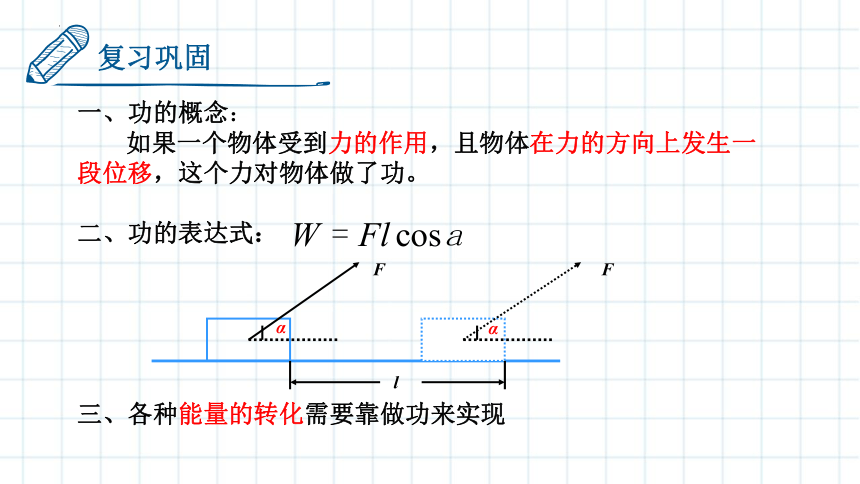
复习巩固
一、功的概念:
如果一个物体受到力的作用,且物体在力的方向上发生一段位移,这个力对物体做了功。
二、功的表达式:
三、各种能量的转化需要靠做功来实现
F
F
l
α
α
导入新课
在工地,用三种方式,将1吨的材料从地面搬到五楼
一:由搬运工搬运,用时4小时
二:用起重机搬运,用时20分钟
三:用升降机搬运,用时10分钟
(1)三种方式搬运,对材料做功是否相同
(2)三种方式对应的时间不同,做功的快慢如何描述
做功相同,时间越短,做功越快
导入新课
在工地,用三种方式,都用时4个小时搬物品从地面搬到五楼
一:由搬运工搬运,搬运1吨物品
二:用起重机搬运,搬运12吨物品
三:用升降机搬运,搬运24吨物品
(1)三种方式搬运,对材料做功是否相同
(2)三种方式对应的时间不同,做功的快慢如何描述
时间相同,做功越多,做功越快
一、功率
一、功率
1.定义:功跟完成这些功与所用时间的比值,叫做功率。
4.物理意义:描述物体做功快慢的物理量。(P越大——做功越快)
5.功率是标量。表示做功过程中能量转化的快慢。
2.定义式:
(单位时间做功的多少)
比值定义法
3.国际单位:瓦特,简称瓦,符号是W
1W=1J/s=1N m/S.
常用单位:千瓦(kW),1kW=1000W=103W
中学生跑步的功率:50W到100W
小汽车的功率:100kW左右
飞机的功率:2500kW作右
火箭的功率:可以达到几十兆瓦
二、功率的另一种表达式
二、功率的另一种表达式
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
“vcosα”整体可称为力方向上的速度
当α=0°时,P=Fv
小球在恒力F拉动,以v匀速直线运动了一段时间t,计算这段时间内F做功的功率
公式 和 都可以用来计算功率。它们在应用时有什么区别?
三、平均功率与瞬时功率
三、平均功率与瞬时功率
1、平均功率:表示在一段时间内力对物体做功的平均快慢
公式
为t时间内的平均速度
α为力与平均速度之间的夹角;
式中: F为恒力(合力、平均力);
2.瞬时功率:表示在某一时刻力对物体做功的快慢
公式:
v为某时刻的瞬时速度
α为力与瞬时速度之间的夹角;
式中: F为某时刻的力(可以是恒力,也可以是变力)
当α=0°时,P=Fv
当作用力方向与运动方向一致时,对 P=Fv 的讨论
2当力F一定时,P与v成正比,即速度越大,功率越大。
v
v
3.当功率P一定时,F与v成反比,即做功的力越大,其速度就越小
1.当速度v一定时 ,F与P成正比,即做功的力越大,它的功率越大
v
v一定:F∝P
F一定:P∝v
P一定:
例1.质量为2 kg的物体,受到24 N竖直向上的拉力,由静止开始运动,求:
(1)5 s内拉力对物体所做的功是多少?
(2)5 s内拉力的平均功率及5 s末拉力的瞬时功率各是多少?(g取10 m/s2)
例2.如图所示,质量为m=2 kg的木块在倾角θ=37°的斜面上由静止开始下滑,木块与斜面间的动摩擦因数为0.5,已知:sin37°=0.6,cos37°=0.8.g取10 m/s2.求:
(1)前2 s内重力做的功;
(2)前2 s内重力的平均功率;
(3)2 s末重力的瞬时功率.
例3.有三个相同的小球,求从同一高度出发点到落地面上重力的平均功率P1、P2、P3的大小关系(忽略空气阻力)
mg
v0
mg
mg
v0
拓展:求三个小球落地时重力的瞬时功率P11、P22 、P33的大小关系?
四、机车启动模型
四、机车启动模型
首先:机车启动一定符合
F牵
f
汽车的瞬时功率
汽车的牵引力
汽车的瞬时速度
汽车在行驶的过程中,发动机的最大功率等于额定功率。
P = F v
①
并且:机车启动的加速度
F牵 – f = ma
②
★注:f 一定
FN
G
机车的两种启动方式
汽车启动(加速运动)的情况有两种:
1、以额定功率P额(或恒定功率)启动;
2、在恒定的牵引力F(或恒定的加速度a)作用下启动。
四、机车启动模型
功率P
一定
牵引
力F牵
速度v
阻力 f 不变
加速度
a
加速度a减小的加速直线运动(变加速直线运动)
达到最大速度vm
有P额=F牵vm =f vm
F牵= f 时
a=0
匀速直线运动
1.当F牵 = f 时速度最大vm
2.先变加速再匀速
3.汽车启动过程始终满足:
P瞬=P额=F牵 v
保持vm
匀速
以额定功率P额(或恒定功率)启动
4.汽车启动结束满足:
P额=F牵 vm =f vm
机车以恒定功率启动的v- t 图
先做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
vm=
f
P
v
t
0
vm
记住两个重要关系式
(1)瞬时加速度公式:
a =
m
f
P
v
(2)最大速度公式
vm=
f
P
加速度a一定
速度v
v=v0+at
牵引力不变
匀加速直线运动
加速度a减小的加速直线运动(变加速直线运动)
功率P
P保持P额
继续加速
达到P额时(P= P额)
F牵 > f(a≠0)
牵引力F牵
速度v
阻力 f 不变
加速度a
达到最大速度vm有 P额=F牵vm =fvm
F牵= f 时
a=0
匀速直线运动
保持 vm 匀速
在恒定的牵引力F′(或恒定的加速度a)作用下启动
1.当F牵= f 时速度最大vm
2.先匀加速再变加速最后匀速
3.汽车匀加速直线运动阶段满足:
P瞬=F′牵v <P额
4.汽车在匀加速直线运动结束时,达到额定功率: P瞬=P额=F′牵v
5.汽车启动结束满足: P额=F牵vm = f vm
机车以恒定加速度启动的v- t 图
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
t
0
Vm=
f
P额
vm
t1
v1
1.当F牵= f 时速度最大vm
2.先匀加速再变加速最后匀速
3.汽车匀加速直线运动阶段满足:
P瞬=F′牵v <P额
4.汽车在匀加速直线运动结束时,达到额定功率: P瞬=P额=F′牵v
5.汽车启动结束满足: P额=F牵vm = f vm
机车启动模型总结
五、曲线运动速率变化与力的关系
(1)当F合方向与v方向的夹角为锐角时,物体运动的速率将增大;
(2)当F合方向与v方向的夹角为钝角时,物体运动的速率将减小;
(3)当F合方向与v方向垂直时,物体运动的速率不变.
vA
F
F1
F2
vA
F
F1
F2
例4.某汽车发动机的额定功率为60 kW,汽车质量为5 t,汽车在运动中所受阻力的大小恒为车重的0.1倍(g取10 m/s2).
(1)若汽车以额定功率启动,则汽车所能达到的最大速度是多少?当汽车速度达到5 m/s时,其加速度是多少?
(2)若汽车以恒定加速度0.5 m/s2启动,则这一过程能维持多长时间?
例5.一列火车总质量m=500 t,发动机的额定功率P=6×105 W,在水平直轨道上行驶时,轨道对火车的阻力Ff是火车重力的。(g取10 m/s2)
(1)求火车在水平直轨道上行驶的最大速度;
(2)在水平直轨道上,发动机以额定功率P工作,求当行驶速度分别为v1=1 m/s和v2=10 m/s时,火车的瞬时加速度a1、a2的大小;
(3)火车在水平直轨道上以36 km/h的速度匀速行驶时,求发动机的实际功率P′;
(4)若火车从静止开始,保持0.5 m/s2的加速度做匀加速直线运动,求这一过程维持的最长时间。
致谢
8.1.2 功率
人教版(2019)高中物理必修二
复习巩固
一、功的概念:
如果一个物体受到力的作用,且物体在力的方向上发生一段位移,这个力对物体做了功。
二、功的表达式:
三、各种能量的转化需要靠做功来实现
F
F
l
α
α
导入新课
在工地,用三种方式,将1吨的材料从地面搬到五楼
一:由搬运工搬运,用时4小时
二:用起重机搬运,用时20分钟
三:用升降机搬运,用时10分钟
(1)三种方式搬运,对材料做功是否相同
(2)三种方式对应的时间不同,做功的快慢如何描述
做功相同,时间越短,做功越快
导入新课
在工地,用三种方式,都用时4个小时搬物品从地面搬到五楼
一:由搬运工搬运,搬运1吨物品
二:用起重机搬运,搬运12吨物品
三:用升降机搬运,搬运24吨物品
(1)三种方式搬运,对材料做功是否相同
(2)三种方式对应的时间不同,做功的快慢如何描述
时间相同,做功越多,做功越快
一、功率
一、功率
1.定义:功跟完成这些功与所用时间的比值,叫做功率。
4.物理意义:描述物体做功快慢的物理量。(P越大——做功越快)
5.功率是标量。表示做功过程中能量转化的快慢。
2.定义式:
(单位时间做功的多少)
比值定义法
3.国际单位:瓦特,简称瓦,符号是W
1W=1J/s=1N m/S.
常用单位:千瓦(kW),1kW=1000W=103W
中学生跑步的功率:50W到100W
小汽车的功率:100kW左右
飞机的功率:2500kW作右
火箭的功率:可以达到几十兆瓦
二、功率的另一种表达式
二、功率的另一种表达式
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
“vcosα”整体可称为力方向上的速度
当α=0°时,P=Fv
小球在恒力F拉动,以v匀速直线运动了一段时间t,计算这段时间内F做功的功率
公式 和 都可以用来计算功率。它们在应用时有什么区别?
三、平均功率与瞬时功率
三、平均功率与瞬时功率
1、平均功率:表示在一段时间内力对物体做功的平均快慢
公式
为t时间内的平均速度
α为力与平均速度之间的夹角;
式中: F为恒力(合力、平均力);
2.瞬时功率:表示在某一时刻力对物体做功的快慢
公式:
v为某时刻的瞬时速度
α为力与瞬时速度之间的夹角;
式中: F为某时刻的力(可以是恒力,也可以是变力)
当α=0°时,P=Fv
当作用力方向与运动方向一致时,对 P=Fv 的讨论
2当力F一定时,P与v成正比,即速度越大,功率越大。
v
v
3.当功率P一定时,F与v成反比,即做功的力越大,其速度就越小
1.当速度v一定时 ,F与P成正比,即做功的力越大,它的功率越大
v
v一定:F∝P
F一定:P∝v
P一定:
例1.质量为2 kg的物体,受到24 N竖直向上的拉力,由静止开始运动,求:
(1)5 s内拉力对物体所做的功是多少?
(2)5 s内拉力的平均功率及5 s末拉力的瞬时功率各是多少?(g取10 m/s2)
例2.如图所示,质量为m=2 kg的木块在倾角θ=37°的斜面上由静止开始下滑,木块与斜面间的动摩擦因数为0.5,已知:sin37°=0.6,cos37°=0.8.g取10 m/s2.求:
(1)前2 s内重力做的功;
(2)前2 s内重力的平均功率;
(3)2 s末重力的瞬时功率.
例3.有三个相同的小球,求从同一高度出发点到落地面上重力的平均功率P1、P2、P3的大小关系(忽略空气阻力)
mg
v0
mg
mg
v0
拓展:求三个小球落地时重力的瞬时功率P11、P22 、P33的大小关系?
四、机车启动模型
四、机车启动模型
首先:机车启动一定符合
F牵
f
汽车的瞬时功率
汽车的牵引力
汽车的瞬时速度
汽车在行驶的过程中,发动机的最大功率等于额定功率。
P = F v
①
并且:机车启动的加速度
F牵 – f = ma
②
★注:f 一定
FN
G
机车的两种启动方式
汽车启动(加速运动)的情况有两种:
1、以额定功率P额(或恒定功率)启动;
2、在恒定的牵引力F(或恒定的加速度a)作用下启动。
四、机车启动模型
功率P
一定
牵引
力F牵
速度v
阻力 f 不变
加速度
a
加速度a减小的加速直线运动(变加速直线运动)
达到最大速度vm
有P额=F牵vm =f vm
F牵= f 时
a=0
匀速直线运动
1.当F牵 = f 时速度最大vm
2.先变加速再匀速
3.汽车启动过程始终满足:
P瞬=P额=F牵 v
保持vm
匀速
以额定功率P额(或恒定功率)启动
4.汽车启动结束满足:
P额=F牵 vm =f vm
机车以恒定功率启动的v- t 图
先做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
vm=
f
P
v
t
0
vm
记住两个重要关系式
(1)瞬时加速度公式:
a =
m
f
P
v
(2)最大速度公式
vm=
f
P
加速度a一定
速度v
v=v0+at
牵引力不变
匀加速直线运动
加速度a减小的加速直线运动(变加速直线运动)
功率P
P
继续加速
达到P额时(P= P额)
F牵 > f(a≠0)
牵引力F牵
速度v
阻力 f 不变
加速度a
达到最大速度vm有 P额=F牵vm =fvm
F牵= f 时
a=0
匀速直线运动
保持 vm 匀速
在恒定的牵引力F′(或恒定的加速度a)作用下启动
1.当F牵= f 时速度最大vm
2.先匀加速再变加速最后匀速
3.汽车匀加速直线运动阶段满足:
P瞬=F′牵v <P额
4.汽车在匀加速直线运动结束时,达到额定功率: P瞬=P额=F′牵v
5.汽车启动结束满足: P额=F牵vm = f vm
机车以恒定加速度启动的v- t 图
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
t
0
Vm=
f
P额
vm
t1
v1
1.当F牵= f 时速度最大vm
2.先匀加速再变加速最后匀速
3.汽车匀加速直线运动阶段满足:
P瞬=F′牵v <P额
4.汽车在匀加速直线运动结束时,达到额定功率: P瞬=P额=F′牵v
5.汽车启动结束满足: P额=F牵vm = f vm
机车启动模型总结
五、曲线运动速率变化与力的关系
(1)当F合方向与v方向的夹角为锐角时,物体运动的速率将增大;
(2)当F合方向与v方向的夹角为钝角时,物体运动的速率将减小;
(3)当F合方向与v方向垂直时,物体运动的速率不变.
vA
F
F1
F2
vA
F
F1
F2
例4.某汽车发动机的额定功率为60 kW,汽车质量为5 t,汽车在运动中所受阻力的大小恒为车重的0.1倍(g取10 m/s2).
(1)若汽车以额定功率启动,则汽车所能达到的最大速度是多少?当汽车速度达到5 m/s时,其加速度是多少?
(2)若汽车以恒定加速度0.5 m/s2启动,则这一过程能维持多长时间?
例5.一列火车总质量m=500 t,发动机的额定功率P=6×105 W,在水平直轨道上行驶时,轨道对火车的阻力Ff是火车重力的。(g取10 m/s2)
(1)求火车在水平直轨道上行驶的最大速度;
(2)在水平直轨道上,发动机以额定功率P工作,求当行驶速度分别为v1=1 m/s和v2=10 m/s时,火车的瞬时加速度a1、a2的大小;
(3)火车在水平直轨道上以36 km/h的速度匀速行驶时,求发动机的实际功率P′;
(4)若火车从静止开始,保持0.5 m/s2的加速度做匀加速直线运动,求这一过程维持的最长时间。
致谢
