2.3 平行线的性质(第1课时) 课件(共22张PPT)- 2023-2024学年七年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 2.3 平行线的性质(第1课时) 课件(共22张PPT)- 2023-2024学年七年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 649.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 06:16:09 | ||
图片预览




文档简介
(共22张PPT)
第二章 相交线与平行线
3.1 平行线的性质
七
下
数
学
2020
1.经历测量、交流、思考等活动归纳并掌握平行线的性质,并能解决一些问题。
2.经历观察、操作、想象、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
学习目标
回顾 & 思考
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
情景引入
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
探索&交流
平行线的性质
1—
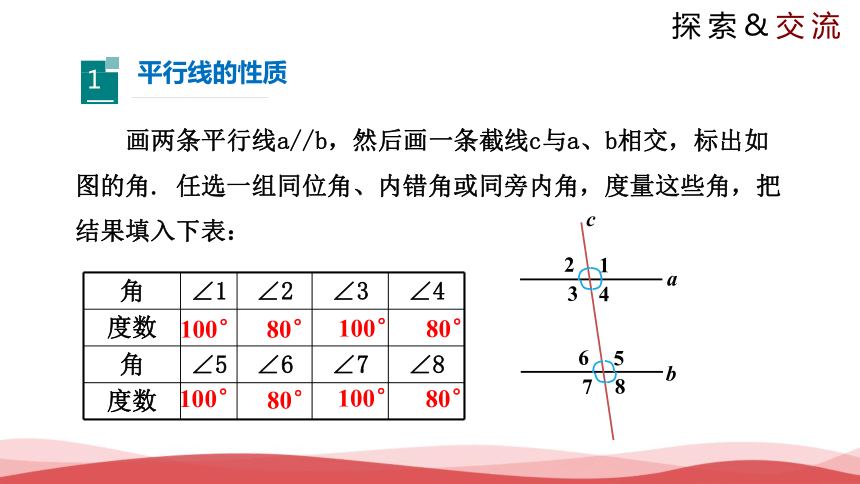
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
a
c
1
2
3
4
5
6
7
8
100°
80°
100°
80°
100°
80°
100°
80°
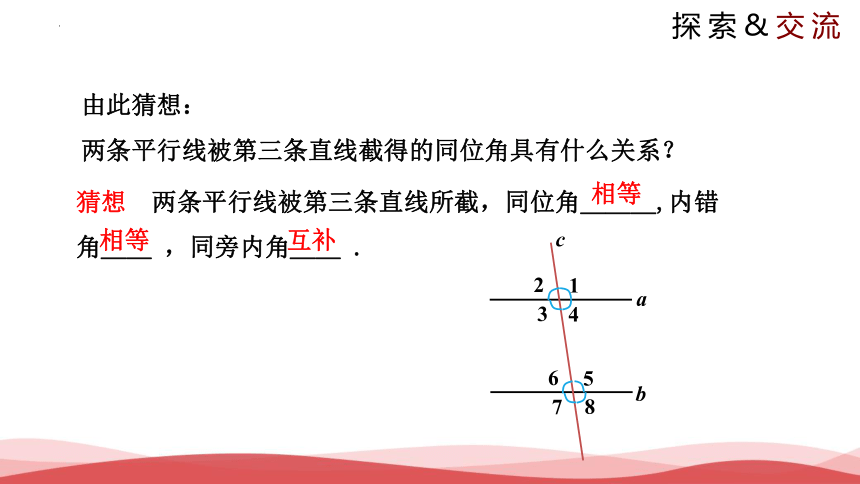
由此猜想:
两条平行线被第三条直线截得的同位角具有什么关系?
猜想 两条平行线被第三条直线所截,同位角___,内错角__ ,同旁内角__ .
相等
相等
互补
探索&交流
b
a
c
1
2
3
4
5
6
7
8
a
b
d
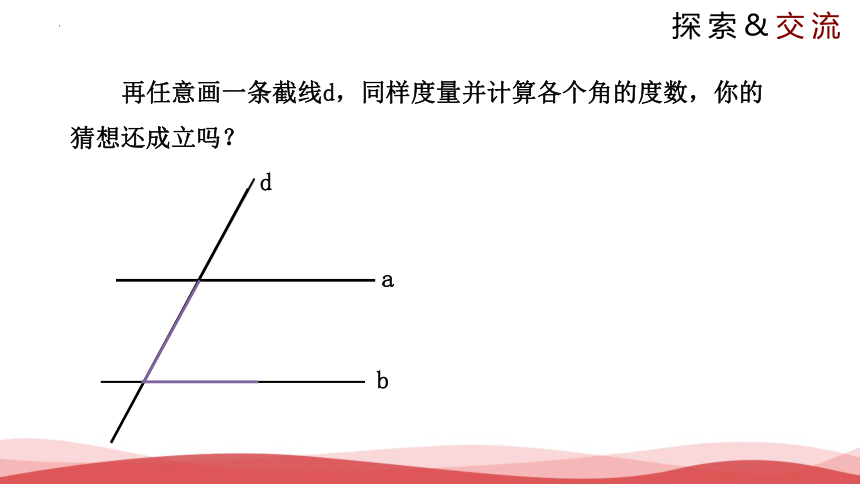
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
探索&交流
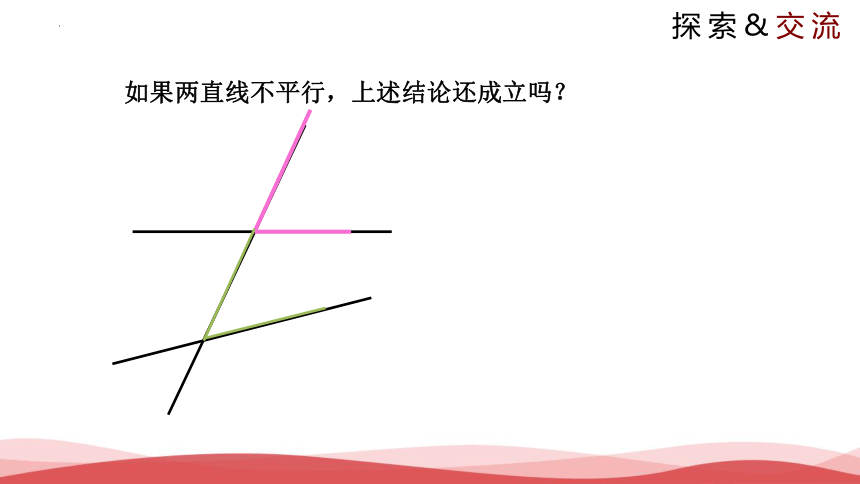
如果两直线不平行,上述结论还成立吗?
探索&交流
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
所以∠1=∠2
(两直线平行,同位角相等)
因为a∥b(已知)
应用格式:
探索&交流
探索&交流
典例精析
例1.如图,直线a∥b,直线c与a,b相交,∠1=70°,
则∠2的大小是( )
A.20° B.50°
C.70° D.110°
C
探索&交流
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”. 类似地,你能由性质 1 推出两条平行线被第三条直线所截,内错角之间的关系吗?
探索&交流
如图,已知a//b,那么 2与 3相等吗?为什么
解:因为a∥b(已知),
所以∠1=∠2(两直线平行,同位角相等).
又因为∠1=∠3(对顶角相等),
所以 ∠2=∠3(等量代换).
b
1
2
a
c
3
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
所以∠2=∠3
(两直线平行,内错角相等)
因为a∥b(已知)
应用格式:
探索&交流
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: 因为a//b(已知),
所以 1= 2
(两直线平行,同位角相等).
因为 1+ 4=180°(补角定义),
所以 2+ 4=180°(等量代换).
探索&交流
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
因为a∥b(已知)
所以∠2+∠4=180 °
(两直线平行,内错角相等)
应用格式:
探索&交流
探索&交流
典例精析
例2.如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD.
因为AE∥BC(已知),
所以∠DAE=∠B(两直线平行,同位角相等),
∠EAC=∠C(两直线平行,内错角相等).
因为∠B=∠C(已知),
所以∠DAE=∠EAC(等量代换).
所以AE平分∠CAD(角平分线的定义).
探索&交流
典例精析
例3.如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120° B.100°
C.80° D.60°
D
探索&交流
做一做
如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
(1)∠1与∠3的大小有什么关系?
(2)反射光线BC与EF也平行吗?
∠2与∠4呢?
1
A
B
C
D
E
F
2
3
4
随堂练习
练习&巩固
1.如果有两条直线被第三条直线所截,那么必定有( )
A. 内错角相等 B. 同位角相等
C. 同旁内角互补 D.以上都不对
D
练习&巩固
D
2.如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
A.25°
B.35°
C.45°
D.50°
练习&巩固
3.如图,如果 AB∥CD∥EF ,那么∠BAC + ∠ACE + ∠CEF =( )
A.180° B.270° C.360° D.540°
C
小结&反思
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
第二章 相交线与平行线
3.1 平行线的性质
七
下
数
学
2020
1.经历测量、交流、思考等活动归纳并掌握平行线的性质,并能解决一些问题。
2.经历观察、操作、想象、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
学习目标
回顾 & 思考
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
情景引入
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
探索&交流
平行线的性质
1—
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
a
c
1
2
3
4
5
6
7
8
100°
80°
100°
80°
100°
80°
100°
80°
由此猜想:
两条平行线被第三条直线截得的同位角具有什么关系?
猜想 两条平行线被第三条直线所截,同位角___,内错角__ ,同旁内角__ .
相等
相等
互补
探索&交流
b
a
c
1
2
3
4
5
6
7
8
a
b
d
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
探索&交流
如果两直线不平行,上述结论还成立吗?
探索&交流
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
所以∠1=∠2
(两直线平行,同位角相等)
因为a∥b(已知)
应用格式:
探索&交流
探索&交流
典例精析
例1.如图,直线a∥b,直线c与a,b相交,∠1=70°,
则∠2的大小是( )
A.20° B.50°
C.70° D.110°
C
探索&交流
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”. 类似地,你能由性质 1 推出两条平行线被第三条直线所截,内错角之间的关系吗?
探索&交流
如图,已知a//b,那么 2与 3相等吗?为什么
解:因为a∥b(已知),
所以∠1=∠2(两直线平行,同位角相等).
又因为∠1=∠3(对顶角相等),
所以 ∠2=∠3(等量代换).
b
1
2
a
c
3
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
所以∠2=∠3
(两直线平行,内错角相等)
因为a∥b(已知)
应用格式:
探索&交流
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: 因为a//b(已知),
所以 1= 2
(两直线平行,同位角相等).
因为 1+ 4=180°(补角定义),
所以 2+ 4=180°(等量代换).
探索&交流
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
因为a∥b(已知)
所以∠2+∠4=180 °
(两直线平行,内错角相等)
应用格式:
探索&交流
探索&交流
典例精析
例2.如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD.
因为AE∥BC(已知),
所以∠DAE=∠B(两直线平行,同位角相等),
∠EAC=∠C(两直线平行,内错角相等).
因为∠B=∠C(已知),
所以∠DAE=∠EAC(等量代换).
所以AE平分∠CAD(角平分线的定义).
探索&交流
典例精析
例3.如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120° B.100°
C.80° D.60°
D
探索&交流
做一做
如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
(1)∠1与∠3的大小有什么关系?
(2)反射光线BC与EF也平行吗?
∠2与∠4呢?
1
A
B
C
D
E
F
2
3
4
随堂练习
练习&巩固
1.如果有两条直线被第三条直线所截,那么必定有( )
A. 内错角相等 B. 同位角相等
C. 同旁内角互补 D.以上都不对
D
练习&巩固
D
2.如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
A.25°
B.35°
C.45°
D.50°
练习&巩固
3.如图,如果 AB∥CD∥EF ,那么∠BAC + ∠ACE + ∠CEF =( )
A.180° B.270° C.360° D.540°
C
小结&反思
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
