7.1.2平面直角坐标系 课件(共24张PPT)-2023-2024学年七年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 7.1.2平面直角坐标系 课件(共24张PPT)-2023-2024学年七年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 801.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览





文档简介
第7.1.2 平面直角坐标系
人教版数学七年级下册
1.认识平面直角坐标系,并能在方格纸上建立适当的平面直角坐标系.
2.了解点与坐标的对应关系.
3.在给定的直角坐标系中,已知点的位置可以写出点的坐标.
4.平面直角坐标系中四个象限的点对应坐标的符号特征.
学习目标
我们用含有两个数的表达方式来表示一个确定的_______,其中两个数各自表示不同的含义,这种________的两个数a与b组成的数对,叫做有序数对,记作 (___,___).
位置
有顺序
a
b
注意:1.数a与b是有顺序的;
2.数a与b是有特定含义的;
3.有序数对表示平面内的点,每个点与有序数对一一对应.
复习引入
0
1
2
3
4
-3
-2
-1
A
B
C
5
-4
如图是一条数轴,数轴上的点与实数是一一对应的.数轴上每个点都对应一个实数,这个实数叫做这个点的坐标.
例如,点A在数轴上的坐标为-4,点B在数轴上的坐标为2.
反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.
例如,数轴上坐标为5的点是点C.
探究新知
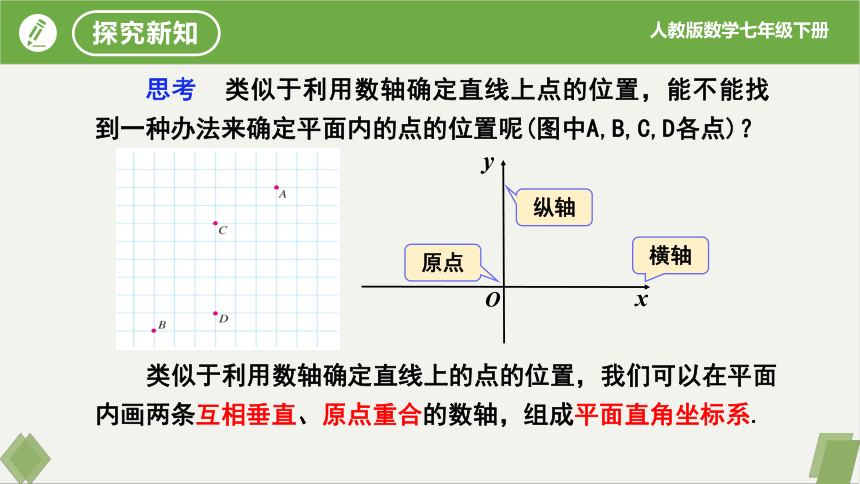
思考 类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(图中A,B,C,D各点)?
类似于利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
x
y
O
横轴
纵轴
原点
探究新知
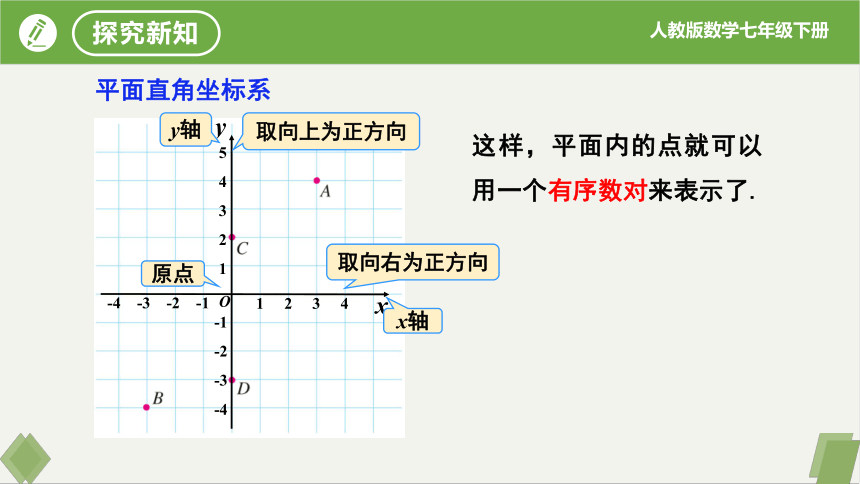
平面直角坐标系
这样,平面内的点就可以用一个有序数对来表示了.
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
x轴
y轴
原点
取向右为正方向
取向上为正方向
探究新知
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
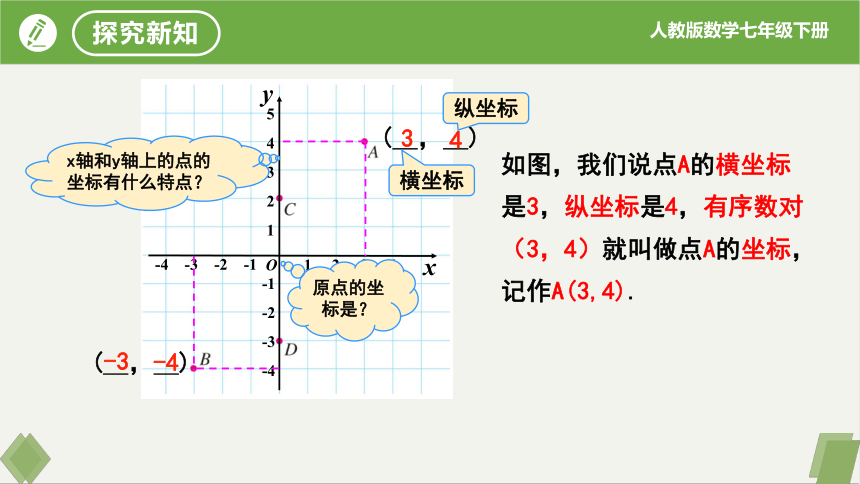
横坐标
纵坐标
如图,我们说点A的横坐标是3,纵坐标是4,有序数对(3,4)就叫做点A的坐标,记作A(3,4).
原点的坐标是?
x轴和y轴上的点的坐标有什么特点?
探究新知
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
( , )
0
0
( , )
0
2
( , )
0
-3
.
( , )
-4
0
.
( , )
2
0
.
你发现什么特点了吗?
原点O的坐标为(0,0);
x轴上的点的纵坐标为0,
例如(1,0),(-1,0)…;
y轴上的点的横坐标为0.
例如(0,1),(0,-1)….
探究新知
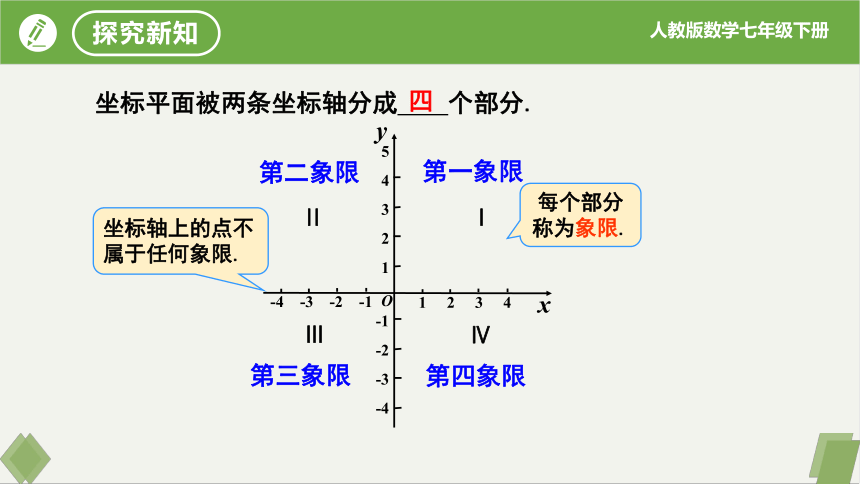
坐标平面被两条坐标轴分成 个部分.
四
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
每个部分称为象限.
第一象限
第二象限
第四象限
第三象限
坐标轴上的点不属于任何象限.
探究新知
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
思考 每个象限内的点具有什么特点?
(+,+)
(-,+)
(-,-)
(+,-)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴
y轴
+
+
-
+
-
-
+
-
纵坐标为0
横坐标为0
探究新知
例1 在平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
A(4,5)
解:如图,先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A.
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,-4)
例题讲解
思考 坐标平面内的点与有序数对(坐标)是什么关系?
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
探究新知
(O) 1 2 3 4 5
6
5
4
3
2
1
D
A
B
C
(0,0)
y
(6,0)
(6,6)
(0,6)
探究 正方形ABCD的边长为6 ,如果以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.
探究新知
请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是什么?与同学们交流一下.
D
A
B
C
x
y
(3,3)
(3,-3)
(-3,3)
(-3,-3)
探究新知
-
+
-
-
+
-
1.根据点所在的位置,用“+”“-”填表.
随堂检测
2.写出图中点B,C,D的坐标.
解:B(-2,3),
C(4,-3),
D(-1,-4)
随堂检测
1.下列说法错误的是 ( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条坐标轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
2.与平面直角坐标系中的点具有一一对应关系的是( )
A.实数 B.有理数 C.有序实数对 D.有序有理数对
A
C
巩固练习
巩固练习
2.如图,点A,B,C,D的坐标分别为
.?
A(3,2),B(2,3),C(-2,3),D(-1,-3)
1.在平面直角坐标系中,点M(m-3,m+1)在x轴上,则点P(m-1,1-m)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.若|a|=5,b2=16,且点M(a,b)在第二象限,则点M的坐标是( )
A.(5,4) B.(-5,4)
C.(-5,-4) D.(5,-4)
拓展训练
B
B
3.请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) B (3,-2) C(0,4) D(-6,0)
E(1,8) F(0,0) G(5,0) H(-6,-4) M (0,-3)
第二象限
第四象限
y轴的正半轴上
x轴的负半轴上
第一象限
坐标原点
x轴的正半轴上
第三象限
y轴的负半轴上
拓展训练
象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+),第二象限:(-,+)
第三象限:(-,-),第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
课堂小结
1.如图,坐标平面上有 A、B、C、D 四点.根据图中各点位置判断,哪一个点在第二象限( )
A.A B.B
C.C D.D
2.已知点 A(?1,?2)和点 B(3,m?1),如果直线 AB//x 轴,那么 m 的值为( )
A.1 B. ?4 C. ?1 D.3
?
A
C
课后作业
课后作业
3.如图,长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
谢谢聆听
人教版数学七年级下册
1.认识平面直角坐标系,并能在方格纸上建立适当的平面直角坐标系.
2.了解点与坐标的对应关系.
3.在给定的直角坐标系中,已知点的位置可以写出点的坐标.
4.平面直角坐标系中四个象限的点对应坐标的符号特征.
学习目标
我们用含有两个数的表达方式来表示一个确定的_______,其中两个数各自表示不同的含义,这种________的两个数a与b组成的数对,叫做有序数对,记作 (___,___).
位置
有顺序
a
b
注意:1.数a与b是有顺序的;
2.数a与b是有特定含义的;
3.有序数对表示平面内的点,每个点与有序数对一一对应.
复习引入
0
1
2
3
4
-3
-2
-1
A
B
C
5
-4
如图是一条数轴,数轴上的点与实数是一一对应的.数轴上每个点都对应一个实数,这个实数叫做这个点的坐标.
例如,点A在数轴上的坐标为-4,点B在数轴上的坐标为2.
反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.
例如,数轴上坐标为5的点是点C.
探究新知
思考 类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(图中A,B,C,D各点)?
类似于利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
x
y
O
横轴
纵轴
原点
探究新知
平面直角坐标系
这样,平面内的点就可以用一个有序数对来表示了.
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
x轴
y轴
原点
取向右为正方向
取向上为正方向
探究新知
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
横坐标
纵坐标
如图,我们说点A的横坐标是3,纵坐标是4,有序数对(3,4)就叫做点A的坐标,记作A(3,4).
原点的坐标是?
x轴和y轴上的点的坐标有什么特点?
探究新知
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
( , )
0
0
( , )
0
2
( , )
0
-3
.
( , )
-4
0
.
( , )
2
0
.
你发现什么特点了吗?
原点O的坐标为(0,0);
x轴上的点的纵坐标为0,
例如(1,0),(-1,0)…;
y轴上的点的横坐标为0.
例如(0,1),(0,-1)….
探究新知
坐标平面被两条坐标轴分成 个部分.
四
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
每个部分称为象限.
第一象限
第二象限
第四象限
第三象限
坐标轴上的点不属于任何象限.
探究新知
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
思考 每个象限内的点具有什么特点?
(+,+)
(-,+)
(-,-)
(+,-)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴
y轴
+
+
-
+
-
-
+
-
纵坐标为0
横坐标为0
探究新知
例1 在平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
A(4,5)
解:如图,先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A.
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,-4)
例题讲解
思考 坐标平面内的点与有序数对(坐标)是什么关系?
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
探究新知
(O) 1 2 3 4 5
6
5
4
3
2
1
D
A
B
C
(0,0)
y
(6,0)
(6,6)
(0,6)
探究 正方形ABCD的边长为6 ,如果以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.
探究新知
请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是什么?与同学们交流一下.
D
A
B
C
x
y
(3,3)
(3,-3)
(-3,3)
(-3,-3)
探究新知
-
+
-
-
+
-
1.根据点所在的位置,用“+”“-”填表.
随堂检测
2.写出图中点B,C,D的坐标.
解:B(-2,3),
C(4,-3),
D(-1,-4)
随堂检测
1.下列说法错误的是 ( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条坐标轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
2.与平面直角坐标系中的点具有一一对应关系的是( )
A.实数 B.有理数 C.有序实数对 D.有序有理数对
A
C
巩固练习
巩固练习
2.如图,点A,B,C,D的坐标分别为
.?
A(3,2),B(2,3),C(-2,3),D(-1,-3)
1.在平面直角坐标系中,点M(m-3,m+1)在x轴上,则点P(m-1,1-m)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.若|a|=5,b2=16,且点M(a,b)在第二象限,则点M的坐标是( )
A.(5,4) B.(-5,4)
C.(-5,-4) D.(5,-4)
拓展训练
B
B
3.请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) B (3,-2) C(0,4) D(-6,0)
E(1,8) F(0,0) G(5,0) H(-6,-4) M (0,-3)
第二象限
第四象限
y轴的正半轴上
x轴的负半轴上
第一象限
坐标原点
x轴的正半轴上
第三象限
y轴的负半轴上
拓展训练
象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+),第二象限:(-,+)
第三象限:(-,-),第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
课堂小结
1.如图,坐标平面上有 A、B、C、D 四点.根据图中各点位置判断,哪一个点在第二象限( )
A.A B.B
C.C D.D
2.已知点 A(?1,?2)和点 B(3,m?1),如果直线 AB//x 轴,那么 m 的值为( )
A.1 B. ?4 C. ?1 D.3
?
A
C
课后作业
课后作业
3.如图,长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
谢谢聆听
