12.7 分数指数幂( 第1课时) 课件(共21张PPT)
文档属性
| 名称 | 12.7 分数指数幂( 第1课时) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 11:43:19 | ||
图片预览








文档简介
(共21张PPT)
12.6 实数的运算
第3课时
2023-2024学年沪教版七年级下册数学课件
1、理解分数指数幂的意义:能将方根与指数幂互化,体会转化思想。(重点)
2、能在简单的运算中运用有理数指数幂的性质进行计算。(难点)
我们知道,减法是加法的逆运算,按照“减去一个数等于加上这个数的相反数”,减法运算可以转化为加法运算;
同样,除法运算也可以转化为乘法运算.那么对互为逆运算的乘方与开方,能否将开方运算转化为某种乘方形式的运算呢
假设
成立,
左边=21,
要使左边=右边成立,则
即 .
所以 .
如何把 表示为2的m次幂的形式呢
我们以前研究的幂都是整数指数幂.
这个m是整数吗
那么
右边= ,
(1)
(2)
(3)
(4)
口答:(用幂的形式表示)
思考
假设
成立,
左边=21,
要使左边=右边成立,则
即 .
所以 .
如何把 表示为2的m次幂的形式呢
思考
我们以前研究的幂都是整数指数幂.
这个m是整数吗
那么
右边= ,
假设
成立,
左边=21,
要使左边=右边成立,则
即 .
所以 .
那么
右边= ,
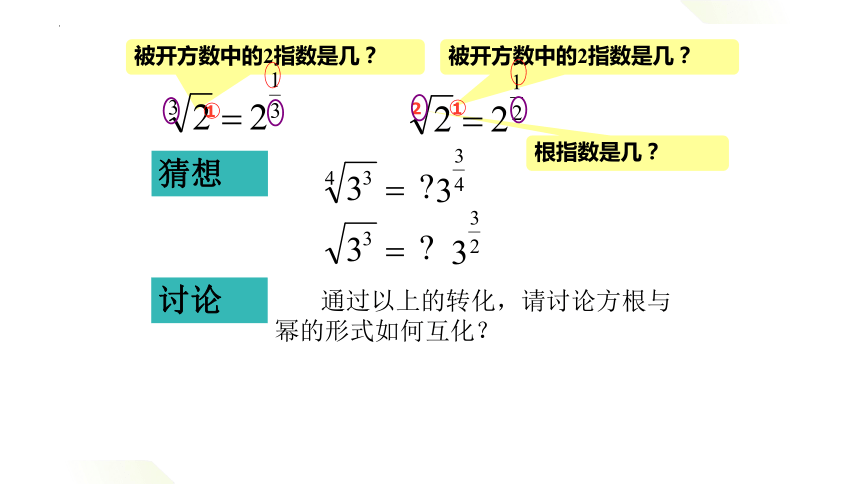
根指数是几?
被开方数中的2指数是几?
被开方数中的2指数是几?
通过以上的转化,请讨论方根与幂的形式如何互化?
讨论
1
猜想
1
2
分数指数幂
(其中m、n为整数, )
上面规定中的 和 叫做分数指数幂, a是底数.
学习新课
把指数的取值范围扩大到分数,我们规定
指数范围扩大到了有理数,方根可以表示为幂的形式,开方运算可以转化为乘方运算.
整数指数幂和分数指数幂统称有理数指数幂 .
有理数指数幂
有理数指数幂的运算性质:
设 , , 、 为有理数,那么
(ⅰ) ,
(ⅱ)
(ⅲ) ,
,
(2)
解:(1)
例1 把下列方根化为幂的形式:
(1) ;(2) ;
(3) ; (4) .
解(3)
(4)
(或 = )
1.(2023春 闵行区期末)下列说法正确的是( ____ )
A.4的平方根是2
B.1的立方根是±1
C.-3没有五次方根
D.0的任何次方根都是0
D
【解析】解:4的平方根是±2,故A不符合题意;
1的立方根是1,故B不符合题意;
-3有五次方根,故C不符合题意;
0的任何次方根都是0,故D符合题意;
故选:D.
2.(2023秋 普陀区校级期末)把 化成幂的形式是 .
【解析】解: .
故答案为: .
例题2 计算:
(1) (2) (3) (4)
解:(1)
一个正数的分数指数幂的值是一个正数.
求分数指数幂的值,就是求一个数的方根,可将分数指数幂表示成方根的形式再求值。如:
(2)
(3)
(4)
例3 将幂的形式转化为方根形式,并用计算器,计算
(保留三位小数):
(1)
(2)
(3)
(4)
解:(1)
(2)
(3)
(4)
≈1.817.
≈4.327.
≈0.629.
≈0.777
1.(2022春 徐汇区校级期中)下列各数中与 相等的是( ____ )
A. B.- C. D.-
A
2.(2022春 青浦区期中)下列说法中,错误的有( ____ )
①2能被6整除;
②把16开平方得16的平方根,表示为 ;
③把237145精确到万位是240000;
④对于实数a,规定
A.1个 B.2个 C.3个 D.4个
D
6能被2整除,故原说法错误
把16开平方得16的平方根,
表示为± ,
把237145精确到万位是2.4×105
对于实数a,规定 ,当m,n不是正整数时不成立,故原说法错误
3.(2021春 静安区校级期末)下列各式中,计算正确的是( ____ )
A.
B.
C.
D.
【解析】解:∵ ,故选项A错误;
,故选项B正确;
,故选项C错误;
,故选项D错误.故选:B.
4.(2023春 徐汇区校级期中)把 写成底数是整数的幂的形式
是 .
【解析】解: = = = ,
∴把 写成底数是整数的幂的形式是 ,
故答案为: .
5.(2023春 长宁区期末)把 表示成幂的形式是 .
【解析】解:把 表示成幂的形式是 .
故答案为 .
6.(2023春 嘉定区期末)利用幂的运算性质计算: × ÷ .
解:原式= × ÷
= × ÷
=
= .
7.(2023春 浦东新区校级期末)利用幂的性质计算:
.
解:原数= × ÷4×
= × ÷22×
=
=
= .
8.(2023春 闵行区期中)计算: .
解:
=
=
=1-3-9
=-11.
谢谢
12.6 实数的运算
第3课时
2023-2024学年沪教版七年级下册数学课件
1、理解分数指数幂的意义:能将方根与指数幂互化,体会转化思想。(重点)
2、能在简单的运算中运用有理数指数幂的性质进行计算。(难点)
我们知道,减法是加法的逆运算,按照“减去一个数等于加上这个数的相反数”,减法运算可以转化为加法运算;
同样,除法运算也可以转化为乘法运算.那么对互为逆运算的乘方与开方,能否将开方运算转化为某种乘方形式的运算呢
假设
成立,
左边=21,
要使左边=右边成立,则
即 .
所以 .
如何把 表示为2的m次幂的形式呢
我们以前研究的幂都是整数指数幂.
这个m是整数吗
那么
右边= ,
(1)
(2)
(3)
(4)
口答:(用幂的形式表示)
思考
假设
成立,
左边=21,
要使左边=右边成立,则
即 .
所以 .
如何把 表示为2的m次幂的形式呢
思考
我们以前研究的幂都是整数指数幂.
这个m是整数吗
那么
右边= ,
假设
成立,
左边=21,
要使左边=右边成立,则
即 .
所以 .
那么
右边= ,
根指数是几?
被开方数中的2指数是几?
被开方数中的2指数是几?
通过以上的转化,请讨论方根与幂的形式如何互化?
讨论
1
猜想
1
2
分数指数幂
(其中m、n为整数, )
上面规定中的 和 叫做分数指数幂, a是底数.
学习新课
把指数的取值范围扩大到分数,我们规定
指数范围扩大到了有理数,方根可以表示为幂的形式,开方运算可以转化为乘方运算.
整数指数幂和分数指数幂统称有理数指数幂 .
有理数指数幂
有理数指数幂的运算性质:
设 , , 、 为有理数,那么
(ⅰ) ,
(ⅱ)
(ⅲ) ,
,
(2)
解:(1)
例1 把下列方根化为幂的形式:
(1) ;(2) ;
(3) ; (4) .
解(3)
(4)
(或 = )
1.(2023春 闵行区期末)下列说法正确的是( ____ )
A.4的平方根是2
B.1的立方根是±1
C.-3没有五次方根
D.0的任何次方根都是0
D
【解析】解:4的平方根是±2,故A不符合题意;
1的立方根是1,故B不符合题意;
-3有五次方根,故C不符合题意;
0的任何次方根都是0,故D符合题意;
故选:D.
2.(2023秋 普陀区校级期末)把 化成幂的形式是 .
【解析】解: .
故答案为: .
例题2 计算:
(1) (2) (3) (4)
解:(1)
一个正数的分数指数幂的值是一个正数.
求分数指数幂的值,就是求一个数的方根,可将分数指数幂表示成方根的形式再求值。如:
(2)
(3)
(4)
例3 将幂的形式转化为方根形式,并用计算器,计算
(保留三位小数):
(1)
(2)
(3)
(4)
解:(1)
(2)
(3)
(4)
≈1.817.
≈4.327.
≈0.629.
≈0.777
1.(2022春 徐汇区校级期中)下列各数中与 相等的是( ____ )
A. B.- C. D.-
A
2.(2022春 青浦区期中)下列说法中,错误的有( ____ )
①2能被6整除;
②把16开平方得16的平方根,表示为 ;
③把237145精确到万位是240000;
④对于实数a,规定
A.1个 B.2个 C.3个 D.4个
D
6能被2整除,故原说法错误
把16开平方得16的平方根,
表示为± ,
把237145精确到万位是2.4×105
对于实数a,规定 ,当m,n不是正整数时不成立,故原说法错误
3.(2021春 静安区校级期末)下列各式中,计算正确的是( ____ )
A.
B.
C.
D.
【解析】解:∵ ,故选项A错误;
,故选项B正确;
,故选项C错误;
,故选项D错误.故选:B.
4.(2023春 徐汇区校级期中)把 写成底数是整数的幂的形式
是 .
【解析】解: = = = ,
∴把 写成底数是整数的幂的形式是 ,
故答案为: .
5.(2023春 长宁区期末)把 表示成幂的形式是 .
【解析】解:把 表示成幂的形式是 .
故答案为 .
6.(2023春 嘉定区期末)利用幂的运算性质计算: × ÷ .
解:原式= × ÷
= × ÷
=
= .
7.(2023春 浦东新区校级期末)利用幂的性质计算:
.
解:原数= × ÷4×
= × ÷22×
=
=
= .
8.(2023春 闵行区期中)计算: .
解:
=
=
=1-3-9
=-11.
谢谢
