21.6二元二次方程组的解法(第1课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 21.6二元二次方程组的解法(第1课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 17:53:39 | ||
图片预览








文档简介
(共26张PPT)
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 21章代数方程
21.6二元二次方程组的解法(第1课时)
学习目标
1、经历探索简单的二元二次方程组解法的过程,会用代入消元法解由一个二元二次方程和一个二元一次方程组成的方程组。(重点)
2、通过解二元二次方程组的活动,体验推理意识、推理能力,以及“消元”和“降次”的策略方法。
复习引入
1、解二元一次方程组的基本思路是什么?
消元
2、解二元一次方程组有哪几种方法?
代入消元法、加减消元法
问题1 什么是二元二次方程组?
仅含有两个未知数,各方程是整式方程,并且含有未知数的项的最高次数为2的方程组叫做二元二次方程组.
问题2 怎样解二元一次方程组
问题3 解二元一次方程组的基本思想是什么?
一元一次方程
消元
问题4 怎样解二元二次方程组
解:把代入,得
整理,得
解这个方程,得
把代入,得
把代入,得
所以,原方程组的解为
代入消元
注意不可回代到方程中
归纳总结
上述解方程组的过程,与用“代入消元法”解二元
一次方程组的过程一样,这样解二元二次方程组的
方法,同样叫做代入消元法。
对于由一个二元一次方程和二元二次方程组成的二
元二次方程组来说,代入消元法是解这类方程组的
基本方法
解方程组:
解:由方程(2),得x=y-1
将x=y-1代入(1),得
整理,得 解得
把 代入(2),得
把 代入(2),得
所以,原方程组的解是
例题1
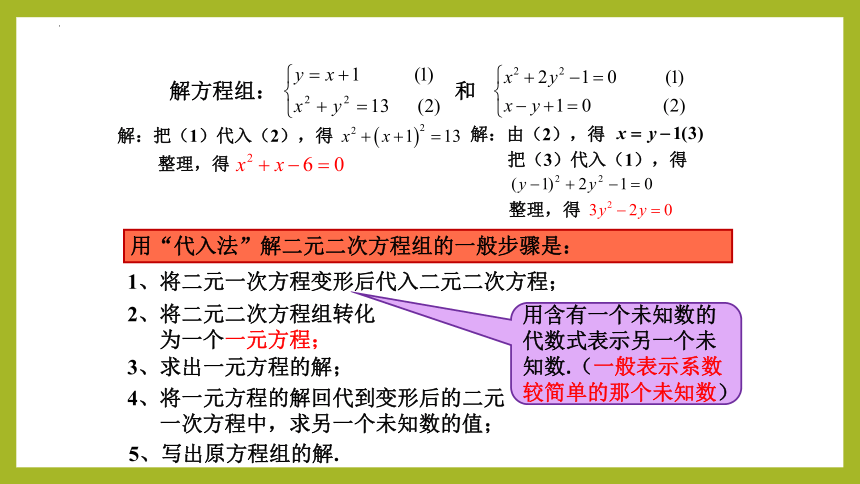
解方程组: 和
用“代入法”解二元二次方程组的一般步骤是:
用含有一个未知数的代数式表示另一个未知数.(一般表示系数较简单的那个未知数)
1、将二元一次方程变形后代入二元二次方程;
2、将二元二次方程组转化
为一个一元方程;
3、求出一元方程的解;
4、将一元方程的解回代到变形后的二元
一次方程中,求另一个未知数的值;
5、写出原方程组的解.
解:把(1)代入(2),得
整理,得
解:由(2),得
把(3)代入(1),得
整理,得
例题2 解方程组:
解法一:由(2),得
把(3)代入(1),得
整理,得
把 代入(3),得
解,得
∴原方程组的解是
例题2
解方程组:
解法二: 方程(1)可变形为:
把(2)代入(3)中,得
即
于是,原方程组化为
解这个二元一次方程组,得
所以,原方程组的解是
归纳
解二元二次方程组的基本思想是“消元”,把它转化为解一元方程的问题.对于含一个二元一次方程的二元二次方程组,采用代入消元法解方程组的一般步骤,可用流程图表述为:
将表达式代入二元二次方程,消去一个未知数,得到一个一元方程(次数不超过二次)
问题6:解二元二次方程组的基本思想是什么?
消元
转化为
一元方程
将二元一次方程变形后代入二元二次方程
“消元”和“降次”
由一个二元一次方程和一个二元二次方程组成的二元二次方程组,一般可以采用“代入法消元”求解.
两个方程之间存在特殊关系,也可以采用“整体代入”的方法,将二元二次方程转化为二元一次方程,达到“降次”的目的.
1.解下列方程组:
(1)
(2)
(3)
练习 21.6(1)
课本练习
2.有一位同学,对例题1的解题过程与我们刚才的解法有所不同,他在
求得 后,后面的解题过程如下:
把 代入(1),得
解这个方程,得
把 代入(1),得
解这个方程,得
∴原方程组的解是
例题1 解方程组:
∴原方程组的解是
这位同学的做法正确吗?为什么?
答:不正确
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
方程组转化为关于x的一元二次方程,可以根据根的判别式来判断方程的根的个数.
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
当m=3时,
∴当m=3时,这个关于x的方程有两个不相等的实数解.
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
当m=4时,
∴当m=4时,这个关于x的方程有两个相等的实数解.
即,
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
当m=5时,
∴当m=5时,这个关于x的方程没有实数解.
1.方程组 的实数解的个数是( ____ )
A.1个 B.2个 C.3个 D.4个
【解析】解: ,
∴(y2-1)(y+3)=0,
∴(y+1)(y-1)(y+3)=0,
C
∴y+1=0或y-1=0或y+3=0,
∴y=-1或y=1或y=-3.
故选:C.
随堂检测
2.关于x、y的方程组 有两个不相同的实数解,则k .
【解析】解: ,
由②得:y=x+3③,将③代入①得:kx2+2(x+3)-8=0,
整理,得:kx2+2x-2=0,
∵关于x、y的方程组 有两个不相同的实数解,
∴kx2+2x-2=0有两个不相同的实数解,
∴Δ=b2-4ac=22-4k×(-2)>0,且k≠0,
∴ 且k≠0.
故答案为: 且k≠0.
3.解方程组: .
【解析】解: ,
由①得:2y=4-x,y= ③,
把③代入②得:x2-2x =0,
x2-x(4-x)=0,x2-4x+x2=0,2x2-4x=0,x2-2x=0,x(x-2)=0,
x=0或x=2,把x=0代入③得:y=2,
把x=2代入③得:y=1,
∴原方程组的解为: 或 .
4.解方程组: .
【解析】解: ,
由①得:(x-y)2=1③,
由②得:x=5-2y④,
把④代入③得:(5-2y-y)2=1,5-3y=±1,
解得:y1=2,y2= ,
把y1=2代入④得:x1=1;把y2= 代入④得:x2= ;
即方程组的解为: , .
5.解方程组: .
【解析】解:由①得:y=2x-6,
把y=2x-6代入②得:x2-x(2x-6)-2(2x-6)2=0,
整理,得:x2-6x+8=0,
解得:x1=2,x2=4;
当x=2时,y=2×2-6=-2;
当x=4时,y=2×4-6=2;
∴方程组的解为: 或 .
6.解方程组:
【解析】解:由①得x=7-2y③,
将③代入②得:(7-2y)2-2y(7-2y)-3y2=0,
整理得:5y2-42y+49=0,
解得: ,y2=7,
分别将 ,y2=7代入③得: ,x2=-7,
∴原方程组的解为: , .
7.解方程组: .
【解析】解:由x-y=4得:x=4+y①,
把①代入x2-6y2=xy中得:(4+y)2-6y2=y(4+y),
解得:y1=2,y2=- ,
当y=2时,x=6,
当y=- 时,x= ,
∴方程组的解为: , .
解二元二次方程组的基本思想是什么?
消元
转化为
一元方程
将二元一次方程变形后代入二元二次方程
“消元”和“降次”
由一个二元一次方程和一个二元二次方程组成的二元二次方程组,一般可以采用“代入法消元”求解.
两个方程之间存在特殊关系,也可以采用“整体代入”的方法,将二元二次方程转化为二元一次方程,达到“降次”的目的.
课堂小结
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 21章代数方程
21.6二元二次方程组的解法(第1课时)
学习目标
1、经历探索简单的二元二次方程组解法的过程,会用代入消元法解由一个二元二次方程和一个二元一次方程组成的方程组。(重点)
2、通过解二元二次方程组的活动,体验推理意识、推理能力,以及“消元”和“降次”的策略方法。
复习引入
1、解二元一次方程组的基本思路是什么?
消元
2、解二元一次方程组有哪几种方法?
代入消元法、加减消元法
问题1 什么是二元二次方程组?
仅含有两个未知数,各方程是整式方程,并且含有未知数的项的最高次数为2的方程组叫做二元二次方程组.
问题2 怎样解二元一次方程组
问题3 解二元一次方程组的基本思想是什么?
一元一次方程
消元
问题4 怎样解二元二次方程组
解:把代入,得
整理,得
解这个方程,得
把代入,得
把代入,得
所以,原方程组的解为
代入消元
注意不可回代到方程中
归纳总结
上述解方程组的过程,与用“代入消元法”解二元
一次方程组的过程一样,这样解二元二次方程组的
方法,同样叫做代入消元法。
对于由一个二元一次方程和二元二次方程组成的二
元二次方程组来说,代入消元法是解这类方程组的
基本方法
解方程组:
解:由方程(2),得x=y-1
将x=y-1代入(1),得
整理,得 解得
把 代入(2),得
把 代入(2),得
所以,原方程组的解是
例题1
解方程组: 和
用“代入法”解二元二次方程组的一般步骤是:
用含有一个未知数的代数式表示另一个未知数.(一般表示系数较简单的那个未知数)
1、将二元一次方程变形后代入二元二次方程;
2、将二元二次方程组转化
为一个一元方程;
3、求出一元方程的解;
4、将一元方程的解回代到变形后的二元
一次方程中,求另一个未知数的值;
5、写出原方程组的解.
解:把(1)代入(2),得
整理,得
解:由(2),得
把(3)代入(1),得
整理,得
例题2 解方程组:
解法一:由(2),得
把(3)代入(1),得
整理,得
把 代入(3),得
解,得
∴原方程组的解是
例题2
解方程组:
解法二: 方程(1)可变形为:
把(2)代入(3)中,得
即
于是,原方程组化为
解这个二元一次方程组,得
所以,原方程组的解是
归纳
解二元二次方程组的基本思想是“消元”,把它转化为解一元方程的问题.对于含一个二元一次方程的二元二次方程组,采用代入消元法解方程组的一般步骤,可用流程图表述为:
将表达式代入二元二次方程,消去一个未知数,得到一个一元方程(次数不超过二次)
问题6:解二元二次方程组的基本思想是什么?
消元
转化为
一元方程
将二元一次方程变形后代入二元二次方程
“消元”和“降次”
由一个二元一次方程和一个二元二次方程组成的二元二次方程组,一般可以采用“代入法消元”求解.
两个方程之间存在特殊关系,也可以采用“整体代入”的方法,将二元二次方程转化为二元一次方程,达到“降次”的目的.
1.解下列方程组:
(1)
(2)
(3)
练习 21.6(1)
课本练习
2.有一位同学,对例题1的解题过程与我们刚才的解法有所不同,他在
求得 后,后面的解题过程如下:
把 代入(1),得
解这个方程,得
把 代入(1),得
解这个方程,得
∴原方程组的解是
例题1 解方程组:
∴原方程组的解是
这位同学的做法正确吗?为什么?
答:不正确
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
方程组转化为关于x的一元二次方程,可以根据根的判别式来判断方程的根的个数.
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
当m=3时,
∴当m=3时,这个关于x的方程有两个不相等的实数解.
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
当m=4时,
∴当m=4时,这个关于x的方程有两个相等的实数解.
即,
3、从方程组 中消去y,得到关于x的二次方程.当m=3
时,这个关于x的方程有几个实数解?当m=4时呢?当m=5时呢?
解:由(2)得,
把(3)代入(1),得
整理,得
当m=5时,
∴当m=5时,这个关于x的方程没有实数解.
1.方程组 的实数解的个数是( ____ )
A.1个 B.2个 C.3个 D.4个
【解析】解: ,
∴(y2-1)(y+3)=0,
∴(y+1)(y-1)(y+3)=0,
C
∴y+1=0或y-1=0或y+3=0,
∴y=-1或y=1或y=-3.
故选:C.
随堂检测
2.关于x、y的方程组 有两个不相同的实数解,则k .
【解析】解: ,
由②得:y=x+3③,将③代入①得:kx2+2(x+3)-8=0,
整理,得:kx2+2x-2=0,
∵关于x、y的方程组 有两个不相同的实数解,
∴kx2+2x-2=0有两个不相同的实数解,
∴Δ=b2-4ac=22-4k×(-2)>0,且k≠0,
∴ 且k≠0.
故答案为: 且k≠0.
3.解方程组: .
【解析】解: ,
由①得:2y=4-x,y= ③,
把③代入②得:x2-2x =0,
x2-x(4-x)=0,x2-4x+x2=0,2x2-4x=0,x2-2x=0,x(x-2)=0,
x=0或x=2,把x=0代入③得:y=2,
把x=2代入③得:y=1,
∴原方程组的解为: 或 .
4.解方程组: .
【解析】解: ,
由①得:(x-y)2=1③,
由②得:x=5-2y④,
把④代入③得:(5-2y-y)2=1,5-3y=±1,
解得:y1=2,y2= ,
把y1=2代入④得:x1=1;把y2= 代入④得:x2= ;
即方程组的解为: , .
5.解方程组: .
【解析】解:由①得:y=2x-6,
把y=2x-6代入②得:x2-x(2x-6)-2(2x-6)2=0,
整理,得:x2-6x+8=0,
解得:x1=2,x2=4;
当x=2时,y=2×2-6=-2;
当x=4时,y=2×4-6=2;
∴方程组的解为: 或 .
6.解方程组:
【解析】解:由①得x=7-2y③,
将③代入②得:(7-2y)2-2y(7-2y)-3y2=0,
整理得:5y2-42y+49=0,
解得: ,y2=7,
分别将 ,y2=7代入③得: ,x2=-7,
∴原方程组的解为: , .
7.解方程组: .
【解析】解:由x-y=4得:x=4+y①,
把①代入x2-6y2=xy中得:(4+y)2-6y2=y(4+y),
解得:y1=2,y2=- ,
当y=2时,x=6,
当y=- 时,x= ,
∴方程组的解为: , .
解二元二次方程组的基本思想是什么?
消元
转化为
一元方程
将二元一次方程变形后代入二元二次方程
“消元”和“降次”
由一个二元一次方程和一个二元二次方程组成的二元二次方程组,一般可以采用“代入法消元”求解.
两个方程之间存在特殊关系,也可以采用“整体代入”的方法,将二元二次方程转化为二元一次方程,达到“降次”的目的.
课堂小结
