21.6二元二次方程组的解法(第2课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 21.6二元二次方程组的解法(第2课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 21章代数方程
21.6二元二次方程组的解法(第2课时)
学习目标
1、经历探索特殊二元二次方程组解法的过程,会用因式分解法解所含的两个方程中至少有一个方程容易化成“两个一次因式的积等于零”的形式的二元二次方程组。(重点)
2、体会“因式分解法”对于特殊方程(组)是一种有效的“降次”策略和方法。
复习回顾:
解方程组:
①
②
①
②
“代入消元法”
“整体代入”思想方法
思考:能用“代入消元法”解的方程组的特点是什么?
引入:我们已经会用代入消元法解由一个二元一次方程和一个二元二次方程组成的二元二次方程组,这节课我们将学习由两个二元二次方程组成的二元二次方程组的解法.
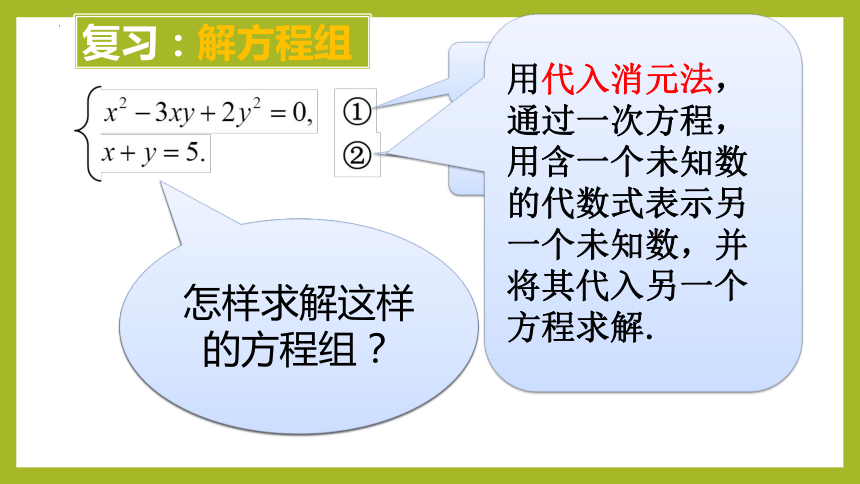
复习:解方程组
二元二次方程
二元一次方程
方程组中的
两个方程有
什么特点?
怎样求解这样的方程组?
用代入消元法,通过一次方程,用含一个未知数的代数式表示另一个未知数,并将其代入另一个方程求解.
复习:解方程组
解:由方程②,得
③
将③代入①,得
整理,得
解方程,得
把 代入③,得
把 代入③,得
∴原方程组的解是
方程组
(2)方程组中的两个方程有什么特点?
(1)能直接使用“代入消元法”解答吗?
①
②
观察
问题 怎样解上面这个二元二次方程组
新课讲解:
解:由(1)得:
得
将它们与(2)分别组成方程组,得
解方程组(1)得
解方程组(2)得
所以原方程组的解是
(省略)
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
特殊的二元二次方程组,所含的两个方程中至少有一个方程容易化成“两个一次因式的积等于零”的形式.
小结:如果二元二次方程组中有一个方程可变形为两个一次因式的乘积等于零的形式,那么解这个方程组的问题可转化为解由一个二元一次方程和一个二元二次方程所组成的方程组.
像这样解特殊的二元二次方程组的方法是“因式分解法”.
①
②
这是一个特殊的二元二次方程组,如果采用前面的方法将方程(1)左边因式分解,再将分解得到的两个方程和(2)组成方程组,这个问题是可以解答的;但进一步观察会发现(2)左边也可以进行因式分解,于是有了下面的解法:
例3 解方程组:
①
②
例3 解方程组:
①
②
原方程组化为:
解: 方程(1)可变形为:
得
方程(2)可变形为
得
分别解这四个方程组,得原方程组的解是
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
两个方程降次(分解因式)
转化
二元一次方程
二元一次方程
四个方程组
解二元二次方程组的基本思路是
“消元”
、
“降次”
.
1.解方程组
时,可以根据其特点把它化成
两个方程组,这两个方程组分别是:
,
.
课本练习
思考:方程组中哪个方程可以
因式分解?
如何分解因式?
2.解下列方程组
(1)
解:将方程①左边分解因式,
可变形为
得
或
.
将它们与方程②分别组成方程组,得:
或
(Ⅰ)
(Ⅱ)
解方程组(Ⅰ),得
解方程组(Ⅱ),得
∴原方程组的解是
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
原方程组化为4个二元一次方程组:
得
或
.
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
(2)
思考方程②的左边如何分解因式?
方程②的左边分解因式,可变形为:
化简得:
(3)
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
得
或
.
即
或
.
原方程组化为4个二元一次方程组:
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
1.解方程组: .
【解析】解:由 x2-4y2=0 得,(x+2y)(x-2y)=0,∴x+2y=0或x-2y=0,
当x+2y=0时,x=-2y,把x=-2y代入x+y=2得,-2y+y=2,
∴y=-2,∴x=-2y=4∴ ,
当x-2y=0时,x=2y,把x=2y代入x+y=2得,2y+y=2,∴y= ,∴x= , ∴ ,
方程组的解为: 或
随堂检测
2.解方程组: .
【解析】解:∵x-y-2=0,∴x-y=2,∴(x-y)2=x2+y2-2xy=4,
∵x2+y2=10,∴10-2xy=4,∴2xy=6,
∴(x+y)2=x2+y2+2xy=10+6=16,∴x+y=4或-4,
∴ 或 ,
解得 或 .
3.解方程组 .
【解析】解: ,
由②得:(2x-y)2=1,
即2x-y=1或2x-y=-1,
所以原方程组可化为两个二元一次方程组: 或
分别解这两个方程组,得原方程组的解是 或 .
4. .
【解析】解: ,
将①因式分解得:(x-4y)(x+y)=0,
∴x-4y=0或x+y=0,
将②因式分解得:(x+2y)2=1,
∴x+2y=1或x+2y=-1,
∴原方程化为: , , , ,
解这些方程组得: , , , .
∴原方程组的解为: , , , ,
5.解方程组:
【解析】解:
由①得:x+3y=0或x-3y=0③,
由②得:x-y=2或x-y=-2④,
由③和④组成方程组 , , , ,
解得: , , , ,
所以原方程组的解为: , , , .
6.解方程组: .
【解析】解: ,
由①,得(x-2y)(x-y)=0,∴x-2y=0或x-y=0.∴x=2y或x=y.
把x=2y代入②,得(2y)2+3y2=4,整理,得y2= ,
∴y=± . ∴ x=± .
把x=y代入②,得(y)2+3y2=4,整理,得y2=1,∴y=±1.∴x=±1.
∴原方程组的解为: , , ,
7.解方程组: .
【解析】解: ,
由②,得(x+2y)(x-2y)=0,
即x+2y=0或x-2y=0③,
由①③组成两个二元一次方程组 , ,
解得: 或 ,
所以原方程组的解是 , .
8.解方程组: .
【解析】解: ,
由①,得x2-xy=0,x(x-y)=0,即x=0或x-y=0③,
由②和③组成两个二元二次方程组 或 ,
解得: , , , ,
所以原方程组的解是 , , , .
课堂小结:
解二元二次方程组的基本思想是“消元”、“降次”. 代入“消元”,因式分解“降次”. 由一个二元一次方程和一个二元二次方程组成的方程组,一般采用代入消元法解. 由两个都是二元二次方程(其中至少有一个可采用因式分解法转化为两个二元一次方程)组成的方程组,采用因式分解法解.
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 21章代数方程
21.6二元二次方程组的解法(第2课时)
学习目标
1、经历探索特殊二元二次方程组解法的过程,会用因式分解法解所含的两个方程中至少有一个方程容易化成“两个一次因式的积等于零”的形式的二元二次方程组。(重点)
2、体会“因式分解法”对于特殊方程(组)是一种有效的“降次”策略和方法。
复习回顾:
解方程组:
①
②
①
②
“代入消元法”
“整体代入”思想方法
思考:能用“代入消元法”解的方程组的特点是什么?
引入:我们已经会用代入消元法解由一个二元一次方程和一个二元二次方程组成的二元二次方程组,这节课我们将学习由两个二元二次方程组成的二元二次方程组的解法.
复习:解方程组
二元二次方程
二元一次方程
方程组中的
两个方程有
什么特点?
怎样求解这样的方程组?
用代入消元法,通过一次方程,用含一个未知数的代数式表示另一个未知数,并将其代入另一个方程求解.
复习:解方程组
解:由方程②,得
③
将③代入①,得
整理,得
解方程,得
把 代入③,得
把 代入③,得
∴原方程组的解是
方程组
(2)方程组中的两个方程有什么特点?
(1)能直接使用“代入消元法”解答吗?
①
②
观察
问题 怎样解上面这个二元二次方程组
新课讲解:
解:由(1)得:
得
将它们与(2)分别组成方程组,得
解方程组(1)得
解方程组(2)得
所以原方程组的解是
(省略)
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
特殊的二元二次方程组,所含的两个方程中至少有一个方程容易化成“两个一次因式的积等于零”的形式.
小结:如果二元二次方程组中有一个方程可变形为两个一次因式的乘积等于零的形式,那么解这个方程组的问题可转化为解由一个二元一次方程和一个二元二次方程所组成的方程组.
像这样解特殊的二元二次方程组的方法是“因式分解法”.
①
②
这是一个特殊的二元二次方程组,如果采用前面的方法将方程(1)左边因式分解,再将分解得到的两个方程和(2)组成方程组,这个问题是可以解答的;但进一步观察会发现(2)左边也可以进行因式分解,于是有了下面的解法:
例3 解方程组:
①
②
例3 解方程组:
①
②
原方程组化为:
解: 方程(1)可变形为:
得
方程(2)可变形为
得
分别解这四个方程组,得原方程组的解是
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
两个方程降次(分解因式)
转化
二元一次方程
二元一次方程
四个方程组
解二元二次方程组的基本思路是
“消元”
、
“降次”
.
1.解方程组
时,可以根据其特点把它化成
两个方程组,这两个方程组分别是:
,
.
课本练习
思考:方程组中哪个方程可以
因式分解?
如何分解因式?
2.解下列方程组
(1)
解:将方程①左边分解因式,
可变形为
得
或
.
将它们与方程②分别组成方程组,得:
或
(Ⅰ)
(Ⅱ)
解方程组(Ⅰ),得
解方程组(Ⅱ),得
∴原方程组的解是
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
原方程组化为4个二元一次方程组:
得
或
.
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
(2)
思考方程②的左边如何分解因式?
方程②的左边分解因式,可变形为:
化简得:
(3)
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
得
或
.
即
或
.
原方程组化为4个二元一次方程组:
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
1.解方程组: .
【解析】解:由 x2-4y2=0 得,(x+2y)(x-2y)=0,∴x+2y=0或x-2y=0,
当x+2y=0时,x=-2y,把x=-2y代入x+y=2得,-2y+y=2,
∴y=-2,∴x=-2y=4∴ ,
当x-2y=0时,x=2y,把x=2y代入x+y=2得,2y+y=2,∴y= ,∴x= , ∴ ,
方程组的解为: 或
随堂检测
2.解方程组: .
【解析】解:∵x-y-2=0,∴x-y=2,∴(x-y)2=x2+y2-2xy=4,
∵x2+y2=10,∴10-2xy=4,∴2xy=6,
∴(x+y)2=x2+y2+2xy=10+6=16,∴x+y=4或-4,
∴ 或 ,
解得 或 .
3.解方程组 .
【解析】解: ,
由②得:(2x-y)2=1,
即2x-y=1或2x-y=-1,
所以原方程组可化为两个二元一次方程组: 或
分别解这两个方程组,得原方程组的解是 或 .
4. .
【解析】解: ,
将①因式分解得:(x-4y)(x+y)=0,
∴x-4y=0或x+y=0,
将②因式分解得:(x+2y)2=1,
∴x+2y=1或x+2y=-1,
∴原方程化为: , , , ,
解这些方程组得: , , , .
∴原方程组的解为: , , , ,
5.解方程组:
【解析】解:
由①得:x+3y=0或x-3y=0③,
由②得:x-y=2或x-y=-2④,
由③和④组成方程组 , , , ,
解得: , , , ,
所以原方程组的解为: , , , .
6.解方程组: .
【解析】解: ,
由①,得(x-2y)(x-y)=0,∴x-2y=0或x-y=0.∴x=2y或x=y.
把x=2y代入②,得(2y)2+3y2=4,整理,得y2= ,
∴y=± . ∴ x=± .
把x=y代入②,得(y)2+3y2=4,整理,得y2=1,∴y=±1.∴x=±1.
∴原方程组的解为: , , ,
7.解方程组: .
【解析】解: ,
由②,得(x+2y)(x-2y)=0,
即x+2y=0或x-2y=0③,
由①③组成两个二元一次方程组 , ,
解得: 或 ,
所以原方程组的解是 , .
8.解方程组: .
【解析】解: ,
由①,得x2-xy=0,x(x-y)=0,即x=0或x-y=0③,
由②和③组成两个二元二次方程组 或 ,
解得: , , , ,
所以原方程组的解是 , , , .
课堂小结:
解二元二次方程组的基本思想是“消元”、“降次”. 代入“消元”,因式分解“降次”. 由一个二元一次方程和一个二元二次方程组成的方程组,一般采用代入消元法解. 由两个都是二元二次方程(其中至少有一个可采用因式分解法转化为两个二元一次方程)组成的方程组,采用因式分解法解.
