18.1.1.2平行四边形的对角线的特征 课件(共22张PPT)
文档属性
| 名称 | 18.1.1.2平行四边形的对角线的特征 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 47.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.1.1.2
平行四边形的
对角线的特征
复习引入
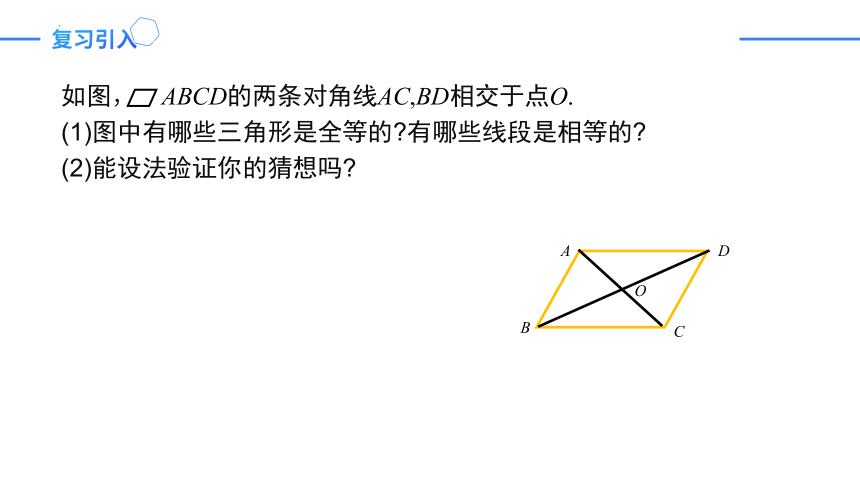
如图, ABCD的两条对角线AC,BD相交于点O.
(1)图中有哪些三角形是全等的 有哪些线段是相等的
(2)能设法验证你的猜想吗
A
B
C
D
O
新知探究
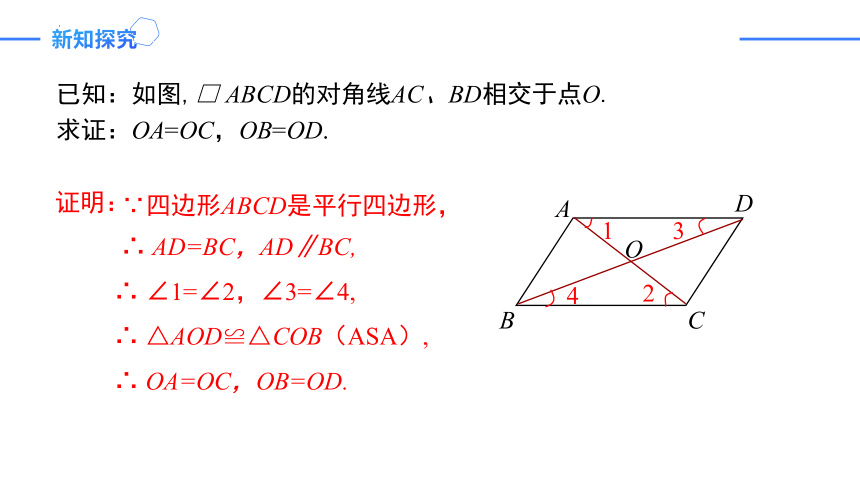
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
平行四边形的性质
新知探究
A
C
D
B
O
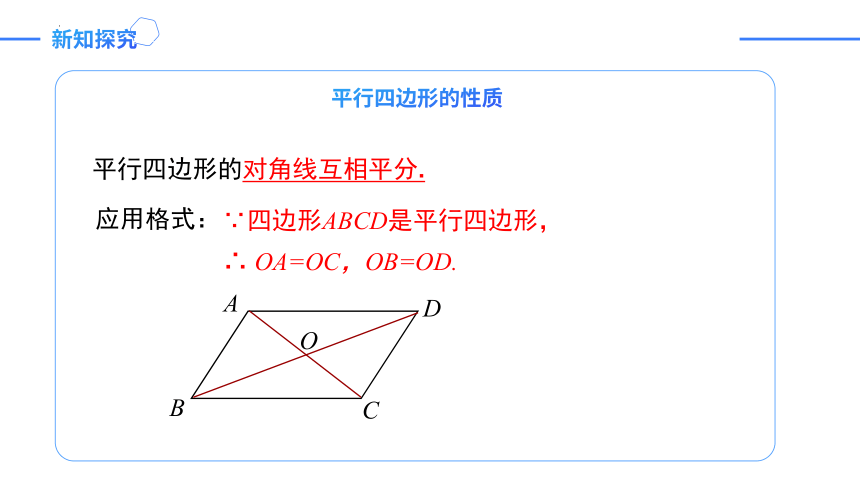
平行四边形的对角线互相平分.
应用格式:
∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
典例精析
例1
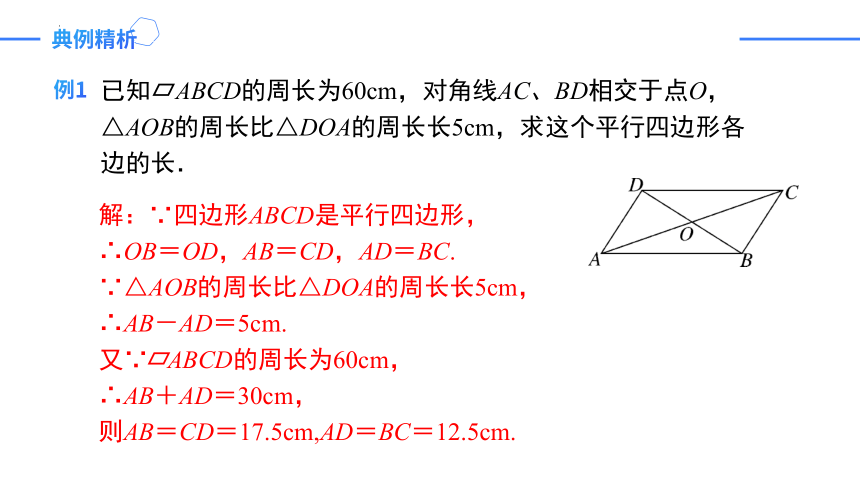
已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,
∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
典例精析
例2
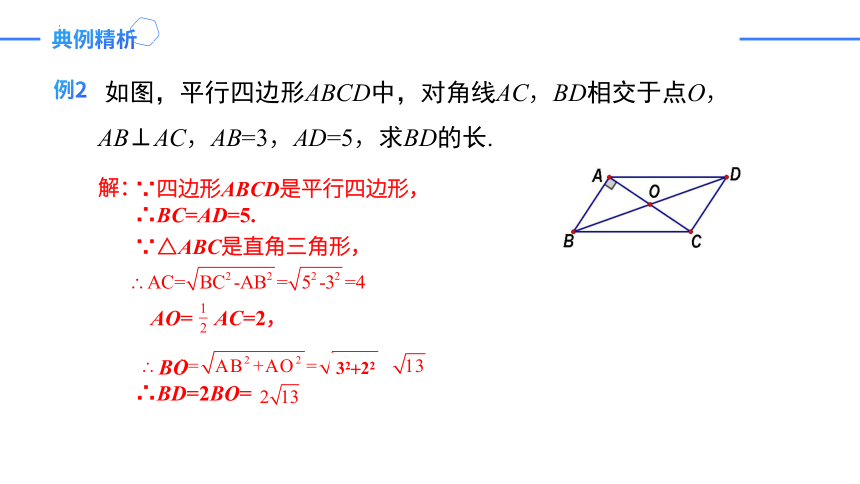
如图,平行四边形ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
解:
∵四边形ABCD是平行四边形,
∴BC=AD=5.
∵△ABC是直角三角形,
AO= AC=2,
∴BD=2BO=
BO
32+22
典例精析
例3
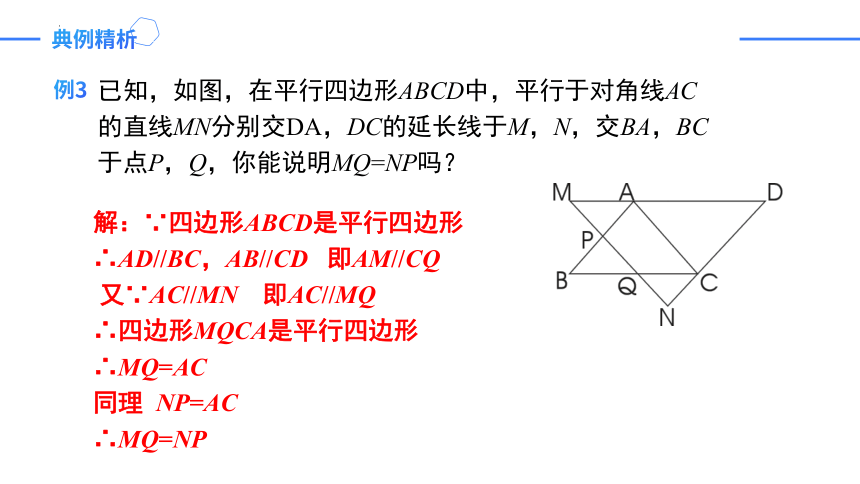
已知,如图,在平行四边形ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于M,N,交BA,BC于点P,Q,你能说明MQ=NP吗?
解:∵四边形ABCD是平行四边形
∴AD//BC,AB//CD 即AM//CQ
又∵AC//MN 即AC//MQ
∴四边形MQCA是平行四边形
∴MQ=AC
同理 NP=AC
∴MQ=NP
典例精析
例4
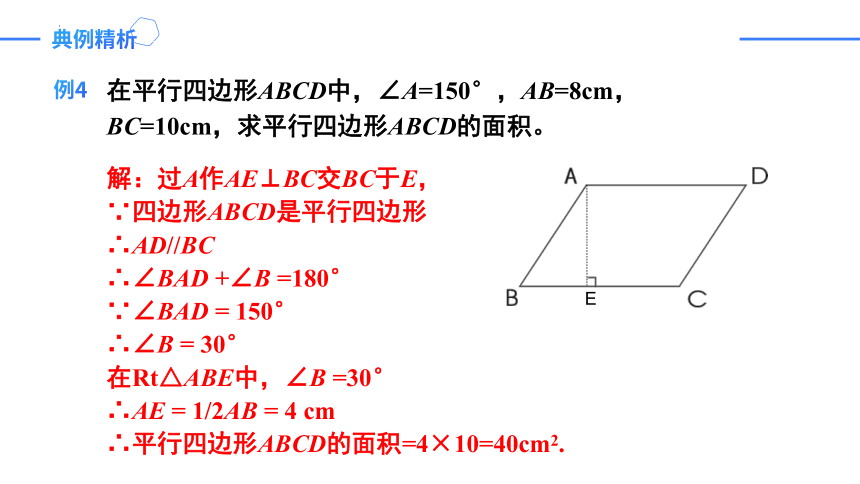
在平行四边形ABCD中,∠A=150°,AB=8cm,
BC=10cm,求平行四边形ABCD的面积。
解:过A作AE⊥BC交BC于E,
∵四边形ABCD是平行四边形
∴AD//BC
∴∠BAD +∠B =180°
∵∠BAD = 150°
∴∠B = 30°
在Rt△ABE中,∠B =30°
∴AE = 1/2AB = 4 cm
∴平行四边形ABCD的面积=4×10=40cm2.
E
典例精析
例5
如图,□ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
在△DOF和△BOE中,
∴△DOF≌△BOE(SAS),∴BE=DF.
典例精析
例6
仅用无刻度直尺作图:过点M作直线l且平分平行四边ABCD的面积.
B
M
C
●
D
A
O
解:如图所示.
典例精析
例7
已知:如图, ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF,
∵ ∠DOE=∠BOF.
∴△DOE≌△BOF.
∴OE=OF.
典例精析
例8
如图1,□ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC相交于点E,F,则OE=OF.若将EF向两边延长与平行四边形的两组对边的延长线分别相交(如图2,图3),OE与OF还相等吗?若相等,请说明理由.
解:图2中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌△COF(AAS),∴OE=OF.图3中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌COF(AAS),∴OE=OF.
平行四边形的性质归纳总结
新知探究
如图,在□ABCD中,有以下结论:
(1)△AOD的周长-△AOB的周长=AD-AB(AD>AB);
(2)S△AOB=S△AOD=S△BOC=S△COD= S□ABCD;
(3)过点O的任意一条直线平分□ABCD的周长和面积;
(4)平行四边形一条对角线的两端点到另一条对角线的距离相等.
归纳总结
平行四
边形对角线的
性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.且与对角线围成的三角形相对的两个全等.
当堂检测
1. 如图,若 ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD的面积为( )cm2.
A.40 B.32 C.36 D.50
A
2.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
C
当堂检测
3.如图,在□ABCD中,对角线AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO B.CD=AB
C.∠BAD=∠BCD D.AC=BD
D
4.如图,□ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
B
当堂检测
5.设点M是□ABCD边AB上任意一点,△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S,则S1,S2,S的数量关系为( )
A.S=S1+S2 B.S>S1+S2
C.S6.□ABCD的对角线AC,BD交于点O,若△AOB的面积为3,则△ABC的面积为________,□ABCD的面积为________.
A
6
12
7. ABCD的对角线AC、BD相交于点O,且AC+BD=40,AB=13,则△OCD的周长为____.
33
当堂检测
8.如图在□ABCD中,AC,BD相交于点O.
已知BC=10,AC=8,BD=14,则△AOD的周长是 ; △DBC 比△ABC的周长大 .
21
6
9.平行四边形两条对角线的长分别为10,16,则它的边长x的取值范围是_________.
3<x<13
当堂检测
10.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长.
8
10
B
C
D
A
O
解:
∴△ABC是直角三角形 ,
又∵AC⊥BC,
∴BC=AD=8,CD=AB=10 .
又∵OA=OC,
∴
∴
?
?
?
∵四边形ABCD是平行四边形,
.
.
当堂检测
11.如图,在□ABCD中,对角线AC,BD交于点O,若DO=1.5 cm,AB=5 cm,BC=4 cm,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
DO=1.5 cm,AB=5 cm,
∴DB=3 cm,CD=AB=5 cm.
又∵BC=4 cm,∴DB2+BC2=CD2,
∴△DBC是直角三角形,且∠CBD=90°,
∴DB⊥BC.∴S□ABCD=BC·DB=3×4=12(cm2).
归纳总结
12.如图,在□ABCD中,AB∶BC=5∶4,对角线AC,BD相交于点O,且BD⊥AD,BD=6.
(1)求AB,BC,AC的值;(2)求□ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OA=OC,OB=OD.
∵AB∶BC=5∶4,∴设AB=5x,则AD=BC=4x.
在Rt△ABD中,根据勾股定理,得AD2+BD2=AB2,即(4x)2+62=(5x)2,
解得x=2.∴AB=10,BC=AD=8.
在Rt△AOD中,AD2+OD2=OA2,∴82+32=OA2,
解得
(2)S□ABCD=AD·BD=8×6=48.
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.1.1.2
平行四边形的
对角线的特征
复习引入
如图, ABCD的两条对角线AC,BD相交于点O.
(1)图中有哪些三角形是全等的 有哪些线段是相等的
(2)能设法验证你的猜想吗
A
B
C
D
O
新知探究
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
平行四边形的性质
新知探究
A
C
D
B
O
平行四边形的对角线互相平分.
应用格式:
∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
典例精析
例1
已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,
∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
典例精析
例2
如图,平行四边形ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
解:
∵四边形ABCD是平行四边形,
∴BC=AD=5.
∵△ABC是直角三角形,
AO= AC=2,
∴BD=2BO=
BO
32+22
典例精析
例3
已知,如图,在平行四边形ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于M,N,交BA,BC于点P,Q,你能说明MQ=NP吗?
解:∵四边形ABCD是平行四边形
∴AD//BC,AB//CD 即AM//CQ
又∵AC//MN 即AC//MQ
∴四边形MQCA是平行四边形
∴MQ=AC
同理 NP=AC
∴MQ=NP
典例精析
例4
在平行四边形ABCD中,∠A=150°,AB=8cm,
BC=10cm,求平行四边形ABCD的面积。
解:过A作AE⊥BC交BC于E,
∵四边形ABCD是平行四边形
∴AD//BC
∴∠BAD +∠B =180°
∵∠BAD = 150°
∴∠B = 30°
在Rt△ABE中,∠B =30°
∴AE = 1/2AB = 4 cm
∴平行四边形ABCD的面积=4×10=40cm2.
E
典例精析
例5
如图,□ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
在△DOF和△BOE中,
∴△DOF≌△BOE(SAS),∴BE=DF.
典例精析
例6
仅用无刻度直尺作图:过点M作直线l且平分平行四边ABCD的面积.
B
M
C
●
D
A
O
解:如图所示.
典例精析
例7
已知:如图, ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF,
∵ ∠DOE=∠BOF.
∴△DOE≌△BOF.
∴OE=OF.
典例精析
例8
如图1,□ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC相交于点E,F,则OE=OF.若将EF向两边延长与平行四边形的两组对边的延长线分别相交(如图2,图3),OE与OF还相等吗?若相等,请说明理由.
解:图2中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌△COF(AAS),∴OE=OF.图3中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌COF(AAS),∴OE=OF.
平行四边形的性质归纳总结
新知探究
如图,在□ABCD中,有以下结论:
(1)△AOD的周长-△AOB的周长=AD-AB(AD>AB);
(2)S△AOB=S△AOD=S△BOC=S△COD= S□ABCD;
(3)过点O的任意一条直线平分□ABCD的周长和面积;
(4)平行四边形一条对角线的两端点到另一条对角线的距离相等.
归纳总结
平行四
边形对角线的
性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.且与对角线围成的三角形相对的两个全等.
当堂检测
1. 如图,若 ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD的面积为( )cm2.
A.40 B.32 C.36 D.50
A
2.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
C
当堂检测
3.如图,在□ABCD中,对角线AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO B.CD=AB
C.∠BAD=∠BCD D.AC=BD
D
4.如图,□ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
B
当堂检测
5.设点M是□ABCD边AB上任意一点,△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S,则S1,S2,S的数量关系为( )
A.S=S1+S2 B.S>S1+S2
C.S
A
6
12
7. ABCD的对角线AC、BD相交于点O,且AC+BD=40,AB=13,则△OCD的周长为____.
33
当堂检测
8.如图在□ABCD中,AC,BD相交于点O.
已知BC=10,AC=8,BD=14,则△AOD的周长是 ; △DBC 比△ABC的周长大 .
21
6
9.平行四边形两条对角线的长分别为10,16,则它的边长x的取值范围是_________.
3<x<13
当堂检测
10.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长.
8
10
B
C
D
A
O
解:
∴△ABC是直角三角形 ,
又∵AC⊥BC,
∴BC=AD=8,CD=AB=10 .
又∵OA=OC,
∴
∴
?
?
?
∵四边形ABCD是平行四边形,
.
.
当堂检测
11.如图,在□ABCD中,对角线AC,BD交于点O,若DO=1.5 cm,AB=5 cm,BC=4 cm,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
DO=1.5 cm,AB=5 cm,
∴DB=3 cm,CD=AB=5 cm.
又∵BC=4 cm,∴DB2+BC2=CD2,
∴△DBC是直角三角形,且∠CBD=90°,
∴DB⊥BC.∴S□ABCD=BC·DB=3×4=12(cm2).
归纳总结
12.如图,在□ABCD中,AB∶BC=5∶4,对角线AC,BD相交于点O,且BD⊥AD,BD=6.
(1)求AB,BC,AC的值;(2)求□ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OA=OC,OB=OD.
∵AB∶BC=5∶4,∴设AB=5x,则AD=BC=4x.
在Rt△ABD中,根据勾股定理,得AD2+BD2=AB2,即(4x)2+62=(5x)2,
解得x=2.∴AB=10,BC=AD=8.
在Rt△AOD中,AD2+OD2=OA2,∴82+32=OA2,
解得
(2)S□ABCD=AD·BD=8×6=48.
