21.7列无理方程解应用题(第3课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 21.7列无理方程解应用题(第3课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 21章代数方程
21.7列无理方程解应用题(第3课时)
学习目标
1、在应用方程解决实际问题的过程中,提高分析问题和解决问题的能力,体会方程的应用价值.(重、难点)
2、会用无理方程解决简单的实际问题.(重点)
复习引入:
1.直角三角形的两条直角边长分别为则斜边的长为 .
2.正数的平方根是 ,它的正的平方根是 .
3.已知则= .
例5.有两块正方形的瓷砖,其中小的一块瓷砖的面积比大的瓷砖的面积小40平方分米,已知大瓷砖的边长长4分米,求这两块瓷砖的面积分别是多少?
分析:方法一:间接设元:设小瓷砖的边长为x分米
边长 面积
小瓷砖
大瓷砖
方法二:直接设元:设小瓷砖的面积为y平方分米
面积 边长
小瓷砖
大瓷砖
解得x=9.
经检验,x=9 是原方程的根,且符合题意
当x=9 时,还十40=9+40=49.
答:这两块瓷砖的面积分别是 9 平方分米和49 平方分米
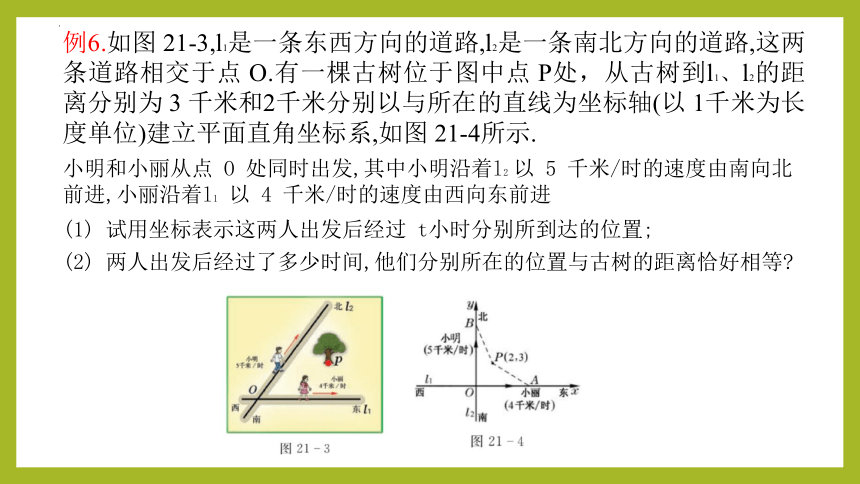
例6.如图 21-3,l1是一条东西方向的道路,l2是一条南北方向的道路,这两条道路相交于点 O.有一棵古树位于图中点 P处,从古树到l1、l2的距离分别为 3 千米和2千米分别以与所在的直线为坐标轴(以 1千米为长度单位)建立平面直角坐标系,如图 21-4所示.
小明和小丽从点 O 处同时出发,其中小明沿着l2 以 5 千米/时的速度由南向北前进,小丽沿着l1 以 4 千米/时的速度由西向东前进
(1) 试用坐标表示这两人出发后经过 t小时分别所到达的位置;
(2) 两人出发后经过了多少时间,他们分别所在的位置与古树的距离恰好相等
分析:根据题意,以点O为原点,L1所在直线为x轴(向东为正方向)、L2所在直线为y轴(向北为正方向),建立直角坐标系(两轴以1千米为长度单位),则点P的坐标为(2,3)
设t小时后两人与点P的距离相等,此时小丽和小明所在的位置分别记为A和B,得A(4t,0),B(0,5t)
因为AP=BP根据两点距离公式得:
解得:
经检验,t1、t2 都是原方程的根,但 t1=0 不合题意,舍去
议一议:
例题5、6是通过哪种方程来求解的?它们与前面所学的列方程解应用题有什么相同点与不同点?
总结
列无理方程(组)解应用题的一般解题步骤:
1.审题 2.设元
3.列方程(组) 4.解方程
5.检验 6.解答。
7.(无理方程要验二次根哦!)(检验是否为原方程的解,验证是否符合题意。)
1. 有一个数,它的正平方根比它的倒数的正平方根的 3 倍多 2,求这个数.
解:设这个数为x,由题意得
答:这个数为9
课本练习
2. 某学校修建两块面积相等的绿地,一块是长方形,另一块是正方形.已知长方形绿地的长比宽多 14 米,且这两块绿地的周长之和为 196 米,那么长方形绿地的宽是多少米
解:设长方形绿地的宽为x米,则长为(x+14)米。由题意,得
解得:x=18
答:长方形绿化地的宽度是18米.
3.试一试.树根下有一蛇洞,树高 15 米.树顶有一只苍鹰,它看见一条蛇迅速地向洞口爬去,在与洞口的距离还有三倍树高时,鹰向蛇的前方直扑过去.如果鹰、蛇的速度相等,那么在蛇离洞口多远处,鹰能抓住蛇 (此题由古代印度数学家婆什迦逻的有趣问题改编而来.)
解:设苍鹰扑向的那一点距离树根的距离为x,由题意可得方程如下:
答:在蛇离洞口20米远处,鹰能抓住蛇
解之得x=20
1.如图,在平面直角坐标系xOy中,点B(5,3),∠OAB=∠B=90°,OC+BC=7,求点C的坐标.
【解析】解:设C(x,3),
∴OC= ,BC=5-x,
∵OC+BC=7,∴ +(5-x)=7,
∴ =x+2,
两边平方得:x2+9=x2+4x+4,解得x= ,
经检验,x= 是原方程的解,
∴C( ,3).
随堂检测
2.如图,矩形草坪ABCD的长AD=14m,宽AB=12m,小华把一根长为28m的绳子的一端固定在点B处,沿草坪边BA、AD走到点P处(点P在边AD上),把长绳PB段拉直并固定在点P处,然后沿草坪边PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.
解:设AP=x m,则DP=(14-x)m,
∴BP= ,CP= ,
∵绳子长28m,
∴ + =28,
∴ =28- ,
解得x=5或x=9,
经检验,x=5,x=9都是原方程的解,
∴AP的长是5m或9m.
3.如图,已知矩形草坪ABCD的长AD=6m,宽AB=4m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
【解析】解:∵四边形ABCD是矩形,____∴∠A=∠D=90°,AB=CD=4,
设AP=x m,则PD=(6-x)m,
∵BP+CP=10,BP= ,CP= ,
∴ + =10,∴ =10- ,
两边平方,得(6-x)2+16=100-20 +16+x2,
整理,得5 =3x+16,两边平方并整理,得x2-6x+9=0,
即(x-3)2=0,所以x1=x2=3,经检验,x=3是方程的解.
答:AP的长为3m.
4.如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
【解析】设AP=xm,则DP=8-x(m).
∵BP= = ,
CP= = ,
又∵BP+CP=10m,∴ + =10.
∴ =10- .
∴(8-x)2+9=100-20 +9+x2.整理,得9+4x=5 .
∴81+72x+16x2=225+25x2.
∴x2-8x+16=0.∴(x-4)2=0.∴x=4.
答:AP的长为4m.
5.如图,已知矩形草坪ABCD的长AD=14m,宽AB=12m,点P在AD上(AP>PD),小华把一根长为28m的绳子一段固定在点B,把长绳PB段拉直并固定在点P,再拉直,长绳的另一端恰好落在点C,求AP的长.
【解析】解:(3)设AP的长为x m,则DP的长为(14-x)m.
由题意,得 =28,
整理,得2 =x+21,
两边平方,得4(144+x2)=x2+42x+441,
即3x2-42x+135=0.
整理,得x2-14x+45=0.
∴(x-5)(x-9)=0.所以x1=5,x2=9,
经检验x1=5,x2=9是原方程的根.
由于AP>DP,所以AP=9m.
6.如图,在矩形ABCD中,AD=8,AB=2,点P在AD上,若PB+PC=10,求AP的长.
________
【解析】解:设AP的长为x,则PD=8-x.
由题意,得 =10,
移项,得 =10- ,
两边平方,得4+(8-x)2=100-20 +4+x2,
整理,得9x2-72x+19=0.
解得x= .
经检验x= 是方程的解.
所以AP的长为 .
7、有一直立杆,它的上部被风吹折,杆顶着地处离杆脚20dm,修好后又被风吹折,因新断处比前次低5dm,故杆顶着地处比前次远10dm,求此杆的高度。
解:设第一次被折断时顶部长x,根部长y,折后构成一个直角三角形,据勾股定理有:
(2)-(1)得x+y=50
即杆的高度为50dm
课堂小结:
1、 首先把实际问题转化为数学问题。
(1)找出等量关系,列出方程;
(2)画出平面几何图形,在图形中寻找等量关系列方程;或建立直角坐标系,在坐标系内寻找等量关系列方程。
2、列无理方程解决应用问题的一般步骤。
列无理方程(组)解应用题的一般解题步骤:
1.审题 2.设元
3.列方程(组) 4.解方程
5.检验 6.解答。
7.(无理方程要验二次根哦!)(检验是否为原方程的解,验证是否符合题意。)
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 21章代数方程
21.7列无理方程解应用题(第3课时)
学习目标
1、在应用方程解决实际问题的过程中,提高分析问题和解决问题的能力,体会方程的应用价值.(重、难点)
2、会用无理方程解决简单的实际问题.(重点)
复习引入:
1.直角三角形的两条直角边长分别为则斜边的长为 .
2.正数的平方根是 ,它的正的平方根是 .
3.已知则= .
例5.有两块正方形的瓷砖,其中小的一块瓷砖的面积比大的瓷砖的面积小40平方分米,已知大瓷砖的边长长4分米,求这两块瓷砖的面积分别是多少?
分析:方法一:间接设元:设小瓷砖的边长为x分米
边长 面积
小瓷砖
大瓷砖
方法二:直接设元:设小瓷砖的面积为y平方分米
面积 边长
小瓷砖
大瓷砖
解得x=9.
经检验,x=9 是原方程的根,且符合题意
当x=9 时,还十40=9+40=49.
答:这两块瓷砖的面积分别是 9 平方分米和49 平方分米
例6.如图 21-3,l1是一条东西方向的道路,l2是一条南北方向的道路,这两条道路相交于点 O.有一棵古树位于图中点 P处,从古树到l1、l2的距离分别为 3 千米和2千米分别以与所在的直线为坐标轴(以 1千米为长度单位)建立平面直角坐标系,如图 21-4所示.
小明和小丽从点 O 处同时出发,其中小明沿着l2 以 5 千米/时的速度由南向北前进,小丽沿着l1 以 4 千米/时的速度由西向东前进
(1) 试用坐标表示这两人出发后经过 t小时分别所到达的位置;
(2) 两人出发后经过了多少时间,他们分别所在的位置与古树的距离恰好相等
分析:根据题意,以点O为原点,L1所在直线为x轴(向东为正方向)、L2所在直线为y轴(向北为正方向),建立直角坐标系(两轴以1千米为长度单位),则点P的坐标为(2,3)
设t小时后两人与点P的距离相等,此时小丽和小明所在的位置分别记为A和B,得A(4t,0),B(0,5t)
因为AP=BP根据两点距离公式得:
解得:
经检验,t1、t2 都是原方程的根,但 t1=0 不合题意,舍去
议一议:
例题5、6是通过哪种方程来求解的?它们与前面所学的列方程解应用题有什么相同点与不同点?
总结
列无理方程(组)解应用题的一般解题步骤:
1.审题 2.设元
3.列方程(组) 4.解方程
5.检验 6.解答。
7.(无理方程要验二次根哦!)(检验是否为原方程的解,验证是否符合题意。)
1. 有一个数,它的正平方根比它的倒数的正平方根的 3 倍多 2,求这个数.
解:设这个数为x,由题意得
答:这个数为9
课本练习
2. 某学校修建两块面积相等的绿地,一块是长方形,另一块是正方形.已知长方形绿地的长比宽多 14 米,且这两块绿地的周长之和为 196 米,那么长方形绿地的宽是多少米
解:设长方形绿地的宽为x米,则长为(x+14)米。由题意,得
解得:x=18
答:长方形绿化地的宽度是18米.
3.试一试.树根下有一蛇洞,树高 15 米.树顶有一只苍鹰,它看见一条蛇迅速地向洞口爬去,在与洞口的距离还有三倍树高时,鹰向蛇的前方直扑过去.如果鹰、蛇的速度相等,那么在蛇离洞口多远处,鹰能抓住蛇 (此题由古代印度数学家婆什迦逻的有趣问题改编而来.)
解:设苍鹰扑向的那一点距离树根的距离为x,由题意可得方程如下:
答:在蛇离洞口20米远处,鹰能抓住蛇
解之得x=20
1.如图,在平面直角坐标系xOy中,点B(5,3),∠OAB=∠B=90°,OC+BC=7,求点C的坐标.
【解析】解:设C(x,3),
∴OC= ,BC=5-x,
∵OC+BC=7,∴ +(5-x)=7,
∴ =x+2,
两边平方得:x2+9=x2+4x+4,解得x= ,
经检验,x= 是原方程的解,
∴C( ,3).
随堂检测
2.如图,矩形草坪ABCD的长AD=14m,宽AB=12m,小华把一根长为28m的绳子的一端固定在点B处,沿草坪边BA、AD走到点P处(点P在边AD上),把长绳PB段拉直并固定在点P处,然后沿草坪边PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.
解:设AP=x m,则DP=(14-x)m,
∴BP= ,CP= ,
∵绳子长28m,
∴ + =28,
∴ =28- ,
解得x=5或x=9,
经检验,x=5,x=9都是原方程的解,
∴AP的长是5m或9m.
3.如图,已知矩形草坪ABCD的长AD=6m,宽AB=4m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
【解析】解:∵四边形ABCD是矩形,____∴∠A=∠D=90°,AB=CD=4,
设AP=x m,则PD=(6-x)m,
∵BP+CP=10,BP= ,CP= ,
∴ + =10,∴ =10- ,
两边平方,得(6-x)2+16=100-20 +16+x2,
整理,得5 =3x+16,两边平方并整理,得x2-6x+9=0,
即(x-3)2=0,所以x1=x2=3,经检验,x=3是方程的解.
答:AP的长为3m.
4.如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
【解析】设AP=xm,则DP=8-x(m).
∵BP= = ,
CP= = ,
又∵BP+CP=10m,∴ + =10.
∴ =10- .
∴(8-x)2+9=100-20 +9+x2.整理,得9+4x=5 .
∴81+72x+16x2=225+25x2.
∴x2-8x+16=0.∴(x-4)2=0.∴x=4.
答:AP的长为4m.
5.如图,已知矩形草坪ABCD的长AD=14m,宽AB=12m,点P在AD上(AP>PD),小华把一根长为28m的绳子一段固定在点B,把长绳PB段拉直并固定在点P,再拉直,长绳的另一端恰好落在点C,求AP的长.
【解析】解:(3)设AP的长为x m,则DP的长为(14-x)m.
由题意,得 =28,
整理,得2 =x+21,
两边平方,得4(144+x2)=x2+42x+441,
即3x2-42x+135=0.
整理,得x2-14x+45=0.
∴(x-5)(x-9)=0.所以x1=5,x2=9,
经检验x1=5,x2=9是原方程的根.
由于AP>DP,所以AP=9m.
6.如图,在矩形ABCD中,AD=8,AB=2,点P在AD上,若PB+PC=10,求AP的长.
________
【解析】解:设AP的长为x,则PD=8-x.
由题意,得 =10,
移项,得 =10- ,
两边平方,得4+(8-x)2=100-20 +4+x2,
整理,得9x2-72x+19=0.
解得x= .
经检验x= 是方程的解.
所以AP的长为 .
7、有一直立杆,它的上部被风吹折,杆顶着地处离杆脚20dm,修好后又被风吹折,因新断处比前次低5dm,故杆顶着地处比前次远10dm,求此杆的高度。
解:设第一次被折断时顶部长x,根部长y,折后构成一个直角三角形,据勾股定理有:
(2)-(1)得x+y=50
即杆的高度为50dm
课堂小结:
1、 首先把实际问题转化为数学问题。
(1)找出等量关系,列出方程;
(2)画出平面几何图形,在图形中寻找等量关系列方程;或建立直角坐标系,在坐标系内寻找等量关系列方程。
2、列无理方程解决应用问题的一般步骤。
列无理方程(组)解应用题的一般解题步骤:
1.审题 2.设元
3.列方程(组) 4.解方程
5.检验 6.解答。
7.(无理方程要验二次根哦!)(检验是否为原方程的解,验证是否符合题意。)
