江西省吉安市永丰中学北师大版数学必修一2.3《函数单调性》课件(23张PPT)
文档属性
| 名称 | 江西省吉安市永丰中学北师大版数学必修一2.3《函数单调性》课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-04 00:00:00 | ||
图片预览



文档简介
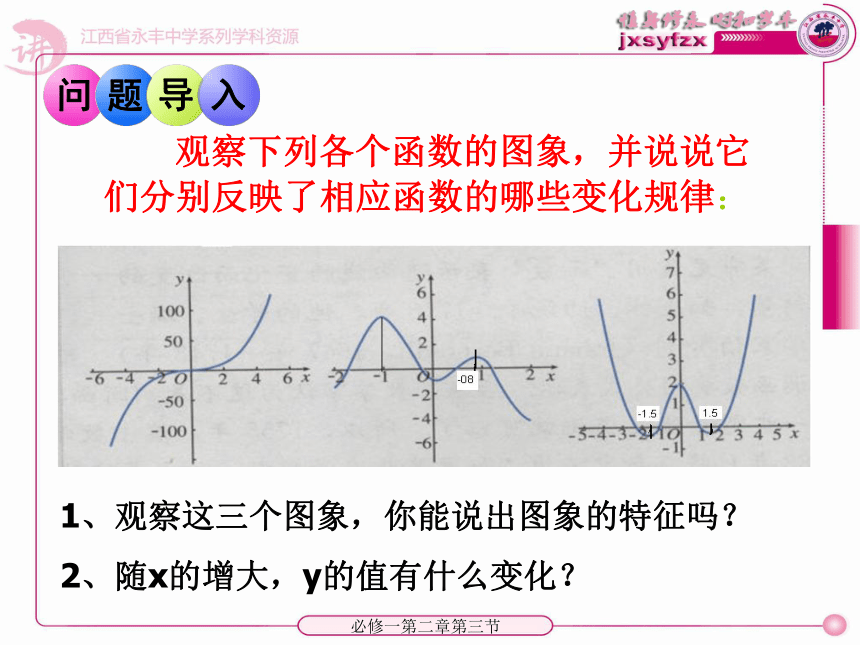
课件23张PPT。函数的单调性永丰中学数学组必修一第二章第三节必修一第二章第三节1. 观察函数图象,从左向右函数图象如何变化?
2. 针对函数y=x2在[0,+∞ )上图像,任取自 变量的两个值,比较其对应函数值的大小.
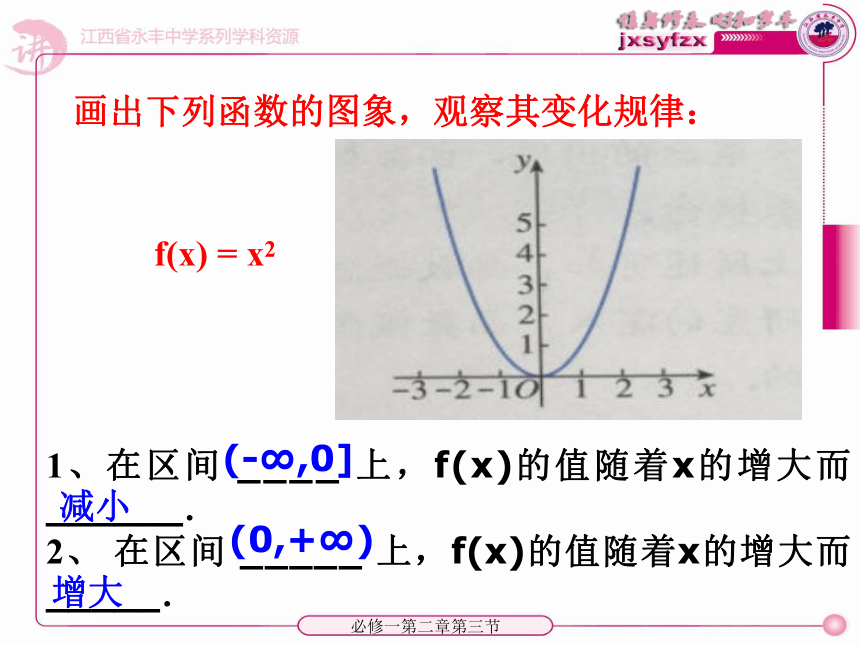
3. 总结归纳出函数图象中自变量x和 y值之间的变化规律.必修一第二章第三节1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
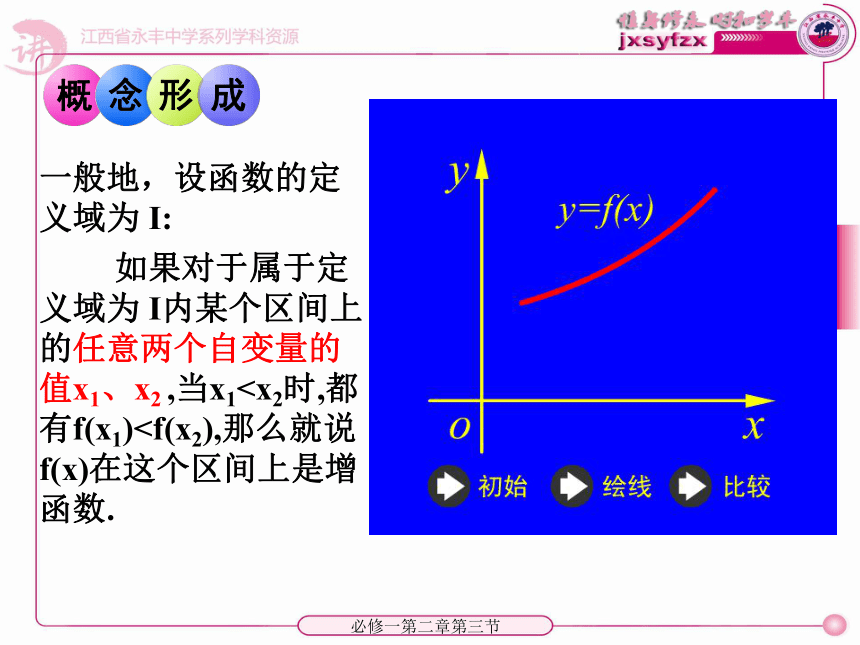
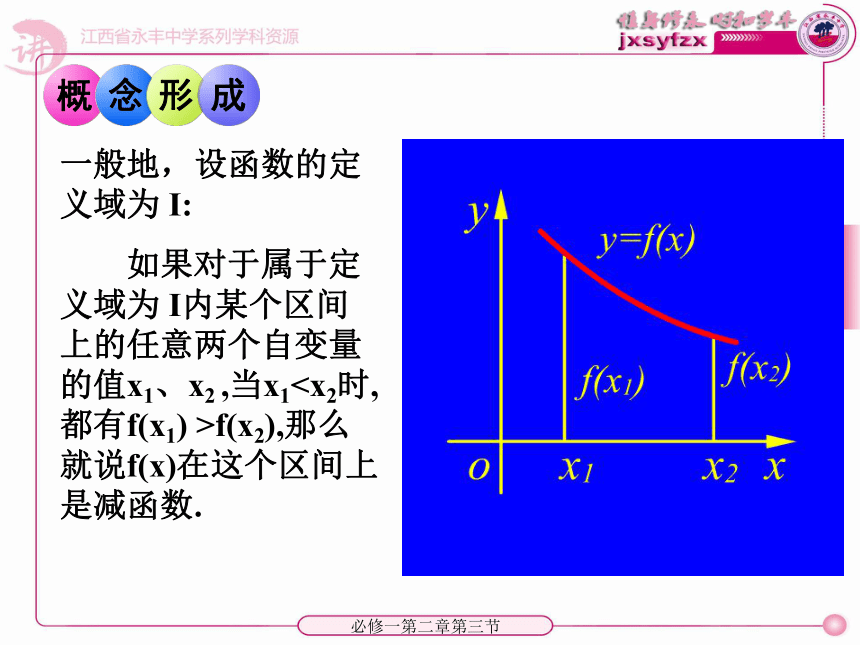
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____. f(x) = x2(-∞,0](0,+∞)增大减小画出下列函数的图象,观察其变化规律: 必修一第二章第三节一般地,设函数的定义域为 I:
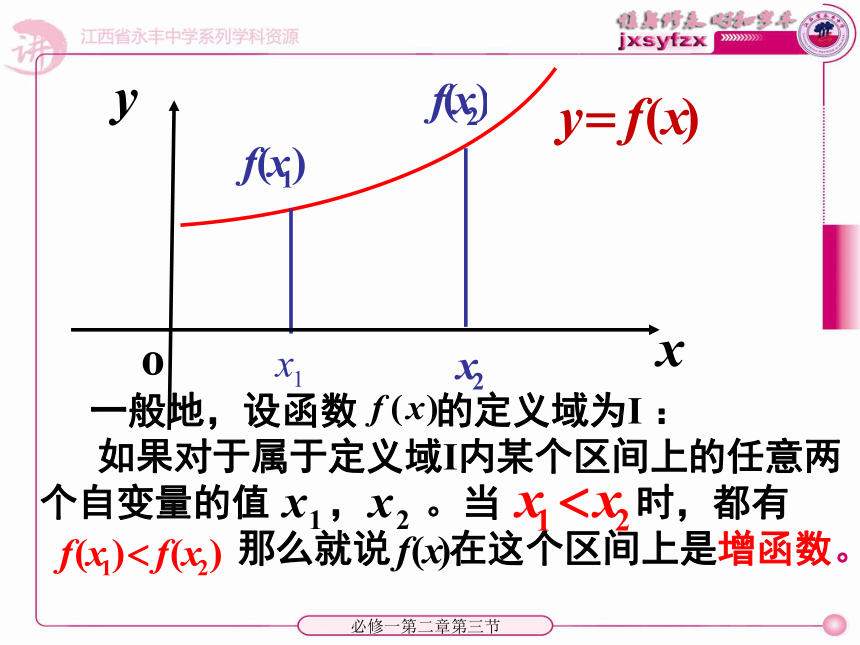
如果对于属于定义域为 I内某个区间上的任意两个自变量的值x1、x2 ,当x1 如果对于属于定义域I内某个区间上的任意两个自变量的值 , 。当 时,都有
那么就说 在这个区间上是增函数。必修一第二章第三节一般地,设函数的定义域为 I:
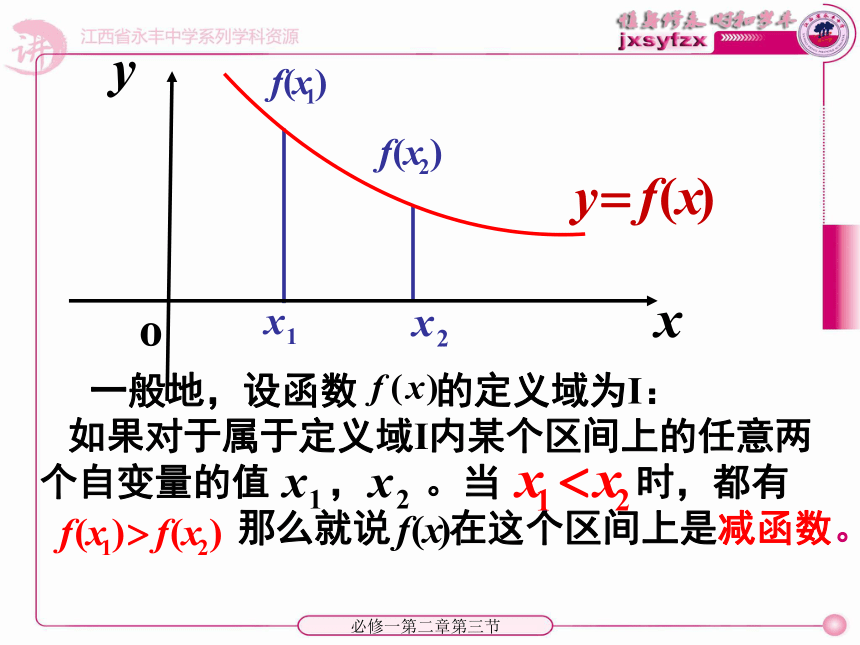
如果对于属于定义域为 I内某个区间上的任意两个自变量的值x1、x2 ,当x1f(x2),那么就说f(x)在这个区间上是减函数.必修一第二章第三节 一般地,设函数 的定义域为I:
如果对于属于定义域I内某个区间上的任意两个自变量的值 , 。当 时,都有
那么就说 在这个区间上是减函数。必修一第二章第三节如果函数 在某个区间上是增
函数或减函数,那么就说函数
在这一区间具有(严格的)单调性,这一区间叫做 的单调区间。必修一第二章第三节1.函数的单调性也叫函
数的增减性2.函数的单调性是对某个区间而言
的,它是一个局部概念.
注:必修一第二章第三节例1 下图是定义在闭区间[-5,5]上的函数 的图象,根据图象说出 的单调区间,以及在每一区间上, 是增函数还是减函数.必修一第二章第三节在区间[-5,-2), [1,3)上是减函数
在区间[-2,1), [3,5)上是增函数.解:函数 的单调区间有
[-5,-2), [-2,1), [1,3), [3,5],O必修一第二章第三节如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.必修一第二章第三节如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.-11o必修一第二章第三节练习:给出下列函数的图象,指出函数的单调区间,
并指明其单调性. 图(1) 图(2) 必修一第二章第三节在
增函数
在
减函数在
增函数
在
减函数在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数在(-∞,+∞)是增函数在(-∞,0)和(0,+∞)是增函数必修一第二章第三节例2 证明函数 在R上是
增函数.证明:设x1,x2是R上的任意两个实数, 且x1 f(x1)-f(x2)=(3x1+2)-(3x2+2)
=3(x1-x2).
由x1 所以, f(x)=3x+2在R上是增函数.
必修一第二章第三节判断函数单调性的方法步骤利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
①任取x1,x2∈D,且x1②作差f(x1)-f(x2);
③变形
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性). (通常是因式分解和配方);必修一第二章第三节例3 证明函数 在(-∞,0)上
是减函数. 由 ,得又由 , 得于是 ,即所以, 在 上是减函数.
证明:设 是 上的任意两个
实数,且 ,则 (- ∞ ,0)(- ∞ ,0 )必修一第二章第三节解:函数图象如右图所示:(-∞,0)和(0,+ ∞)是两个单调减区间。思考:能否说该函数在区间(-∞,0)∪(0,+ ∞)上是单调减函数?不能必修一第二章第三节 1、判断f(x)=x2-1在(0,+ ∞)上是增函数还是减函数?
2、判断f(x)=-x2+2x在(- ∞,0)上是增函数还是减函数?增函数增函数必修一第二章第三节 1、函数单调性是对定义域的某个区间而言的,反映的是在这一区间上函数值随自变量变化的性质.
2、判断函数单调性的方法:
(1)利用图象:
在单调区间上,增函数图象从左向右是上升的,减函数图象是下降的.
(2)利用定义:
用定义证明函数单调性的一般步骤:
任意取值→作差变形→判断符号→ 得出结论.课堂小结,知识再现必修一第二章第三节1、已知
2、若函数
3、因为函数 在区间上 都是减函数,所以
在上 是减函数。 判断下列说法是否判断必修一第二章第三节
2. 针对函数y=x2在[0,+∞ )上图像,任取自 变量的两个值,比较其对应函数值的大小.
3. 总结归纳出函数图象中自变量x和 y值之间的变化规律.必修一第二章第三节1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____. f(x) = x2(-∞,0](0,+∞)增大减小画出下列函数的图象,观察其变化规律: 必修一第二章第三节一般地,设函数的定义域为 I:
如果对于属于定义域为 I内某个区间上的任意两个自变量的值x1、x2 ,当x1
那么就说 在这个区间上是增函数。必修一第二章第三节一般地,设函数的定义域为 I:
如果对于属于定义域为 I内某个区间上的任意两个自变量的值x1、x2 ,当x1
如果对于属于定义域I内某个区间上的任意两个自变量的值 , 。当 时,都有
那么就说 在这个区间上是减函数。必修一第二章第三节如果函数 在某个区间上是增
函数或减函数,那么就说函数
在这一区间具有(严格的)单调性,这一区间叫做 的单调区间。必修一第二章第三节1.函数的单调性也叫函
数的增减性2.函数的单调性是对某个区间而言
的,它是一个局部概念.
注:必修一第二章第三节例1 下图是定义在闭区间[-5,5]上的函数 的图象,根据图象说出 的单调区间,以及在每一区间上, 是增函数还是减函数.必修一第二章第三节在区间[-5,-2), [1,3)上是减函数
在区间[-2,1), [3,5)上是增函数.解:函数 的单调区间有
[-5,-2), [-2,1), [1,3), [3,5],O必修一第二章第三节如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.必修一第二章第三节如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.-11o必修一第二章第三节练习:给出下列函数的图象,指出函数的单调区间,
并指明其单调性. 图(1) 图(2) 必修一第二章第三节在
增函数
在
减函数在
增函数
在
减函数在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数在(-∞,+∞)是增函数在(-∞,0)和(0,+∞)是增函数必修一第二章第三节例2 证明函数 在R上是
增函数.证明:设x1,x2是R上的任意两个实数, 且x1
由x1
必修一第二章第三节判断函数单调性的方法步骤利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
①任取x1,x2∈D,且x1
③变形
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性). (通常是因式分解和配方);必修一第二章第三节例3 证明函数 在(-∞,0)上
是减函数. 由 ,得又由 , 得于是 ,即所以, 在 上是减函数.
证明:设 是 上的任意两个
实数,且 ,则 (- ∞ ,0)(- ∞ ,0 )必修一第二章第三节解:函数图象如右图所示:(-∞,0)和(0,+ ∞)是两个单调减区间。思考:能否说该函数在区间(-∞,0)∪(0,+ ∞)上是单调减函数?不能必修一第二章第三节 1、判断f(x)=x2-1在(0,+ ∞)上是增函数还是减函数?
2、判断f(x)=-x2+2x在(- ∞,0)上是增函数还是减函数?增函数增函数必修一第二章第三节 1、函数单调性是对定义域的某个区间而言的,反映的是在这一区间上函数值随自变量变化的性质.
2、判断函数单调性的方法:
(1)利用图象:
在单调区间上,增函数图象从左向右是上升的,减函数图象是下降的.
(2)利用定义:
用定义证明函数单调性的一般步骤:
任意取值→作差变形→判断符号→ 得出结论.课堂小结,知识再现必修一第二章第三节1、已知
2、若函数
3、因为函数 在区间上 都是减函数,所以
在上 是减函数。 判断下列说法是否判断必修一第二章第三节
