2024年 九年级数学中考复习 相似三角形综合解答题 专题提升训练(含答案)
文档属性
| 名称 | 2024年 九年级数学中考复习 相似三角形综合解答题 专题提升训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 836.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 07:47:10 | ||
图片预览




文档简介
2024年春九年级数学中考复习《相似三角形综合解答题》专题提升训练(附答案)
1.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证EG2=GF AF;
(3)若AG=3,EG=,求BE的长.
2.如图,在梯形中,,,,点、分别在线段、上,.的延长线交边于点,交于点、其延长线交的延长线于点.
(1)求证:;
(2)设,的面积为,求关于的函数解析式,并写出它的定义域;
(3)联结,当与相似时,求的长.
3.如图,在中,,为上一点,经过点的分别交,于点,,与相切于点,连接,相交于点.
(1)求证:平分;
(2)求证:;
(3)若,,求的长.
4.如图,抛物线与轴交于、两点,与轴正半轴交于点,已知.
(1)求抛物线的解析式及顶点的坐标.
(2)若为第一象限抛物线上的一个动点,为轴上的一点,过点作轴,若与以点、、为顶点的三角形相似,求动点的坐标.
5.【问题背景】(1)如图1,,,.求证:;
【变式迁移】(2)如图2,E为正方形ABCD外一点,,过点D作,垂足为F,连接CF.求的值;
【拓展创新】(3)如图3,A是内一点,,,,,,直接写出AB的长.
6.如图,为正方形对角线上的一点,连接并延长交于点,过作分别交,于,.
(1)如图1,求证:;
(2)如图2,点与点关于直线对称,连接并延长交直线于点,连接.
①设的度数为,求的度数:
②猜想与之间的数量关系,并证明.
7.在矩形中,点是对角线、的交点,直角的顶点与重合,、分别与、边相交于、,连接,(为常数).
(1)发现问题:如图1,若,猜想:________;
(2)类比探究:如图2,,探究线段,之间的数量关系,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,若,,,求的长.
8.综合与实践
【问题背景】
如图1,矩形中,.点E为边上一点,沿直线将矩形折叠,使点C落在边的点处.
【问题解决】
(1)填空:的长为______.
(2)如图2,将沿线段向右平移,使点与点B重合,得到与交于点F,与交于点G.求的长;
【拓展探究】
(3)在图2中,连接,则四边形是平行四边形吗?若是,请予以证明;若不是,请说明理由.
9.在菱形中,,点、分别是边、上两点,满足,与相交于点.
(1)如图1,连接.求证:;
(2)如图2,连接.
①求证:;
②若,,求线段的长(用含、的代数式表示).
10.(1)如图1,,垂足为D,,垂足为E,AD与BE相交于点F,连接ED.你能在图中找出一对相似三角形,并说明相似的理由吗?
(2)如图2,在中,,,,重足为E,P为AB上一点,于D,交BE于F.求证:;
(3)如图3,在中,,M为AC上一点,连接BM,,,,请直接写出BC的长.
11.【问题探究】
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.
①请探究AD与BD之间的位置关系?并加以证明.
②若AC=BC=,DC=CE=,求线段AD的长.
【拓展延伸】
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
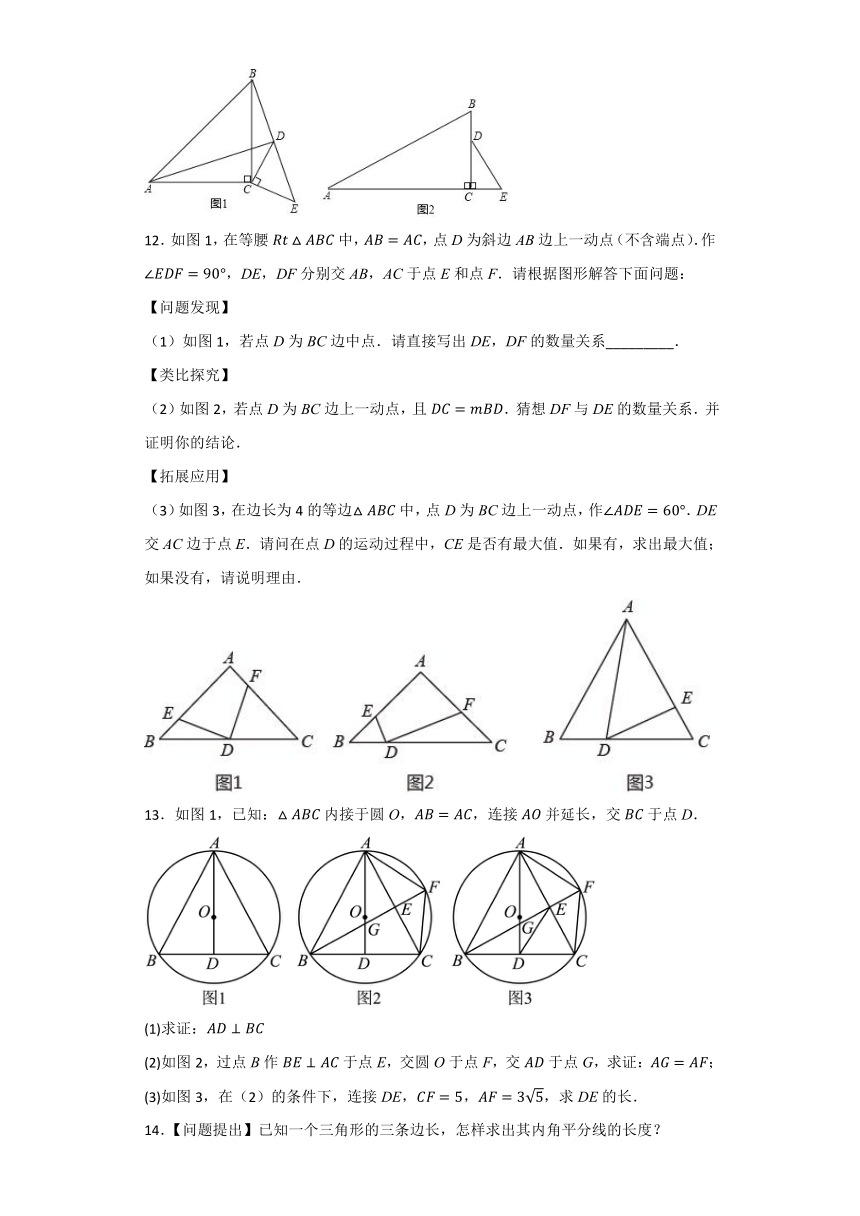
12.如图1,在等腰中,,点D为斜边AB边上一动点(不含端点).作,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题:
【问题发现】
(1)如图1,若点D为BC边中点.请直接写出DE,DF的数量关系_________.
【类比探究】
(2)如图2,若点D为BC边上一动点,且.猜想DF与DE的数量关系.并证明你的结论.
【拓展应用】
(3)如图3,在边长为4的等边中,点D为BC边上一动点,作.DE交AC边于点E.请问在点D的运动过程中,CE是否有最大值.如果有,求出最大值;如果没有,请说明理由.
13.如图1,已知:内接于圆O,,连接并延长,交于点D.
(1)求证:
(2)如图2,过点B作于点E,交圆O于点F,交于点G,求证:;
(3)如图3,在(2)的条件下,连接DE,,,求DE的长.
14.【问题提出】已知一个三角形的三条边长,怎样求出其内角平分线的长度?
【问题转化】
(1)已知:如图1,中,是内角平分线.求证:;
(2)已知:如图2,内接于,延长的内角平分线交于点.求证:;
【问题解决】
(3)已知:如图3,中,,,,是的内角平分线.求的长;
(4)已知:如图3,中,,,,是的内角平分线.请直接写出求的计算公式:__________.
15.如图,⊙O是△ABC的外接圆,AB为直径,弦AD平分∠BAC,过点D作射线AC的垂线,垂足为M,点E为线段AB上的动点.
(1)求证:MD是⊙O的切线;
(2)若∠B=30°,AB=8,在点E运动过程中,EC+EM是否存在最小值?若存在,请求出最小值;若不存在,说明理由;
(3)若点E恰好运动到∠ACB的角平分线上,连接CE并延长,交⊙O于点F,交AD于点P,连接AF,CP=3,EF=4,求AF的长.
16.如图,在中,,,点为的中点,连接,将线段绕点顺时针旋转得到线段,且交线段于点,的平分线交于点.
(1)如图1,若,则线段与的数量关系是________,________;
(2)如图2,在(1)的条件下,过点作交于点,连接,.
①试判断四边形的形状,并说明理由;
②求证:;
(3)如图3,若,,过点作交于点,连接,,请直接写出的值(用含的式子表示).
17.在矩形ABCD的CD边上取一点E,将沿BE翻折至的位置.
(1)如图1,当点F落在矩形ABCD内部时,连接CF并延长,交AD于点G,若,,,则GF的长度为________________;
(2)如图2,当点C恰好落在AD边上点F处时,若,且,求BC的长;
(3)如图3,当点C恰好落在AD边上点F处时,延长EF,与的角平分线交于点M,BM交AD于点N,当时,求的值.
18.【基础探究】(1)如图①,在中,为上一点,,交延长线于点,若,求的长.
【拓展延伸】(2)如图②,在中,为上一点,,交延长线于点,,, ,则 .
【拓展延伸】(3)如图③,点为四边形内部一点,且有,,于点,为上一点,,若,,则的面积为 .
19.【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形中,点,分别是边,上的点,连接,,且于点,若,,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
【初步运用】
(2)如图2,在中,,,点为的中点,连接,过点作于点,交于点,求的值.
【灵活运用】
(3)如图3,在四边形中,,,,,点,分别在边,上,且,垂足为,则__________________.
20.如图,在平面直角坐标系中,抛物线:经过点和.
(1)求抛物线的对称轴.
(2)当时,将抛物线向左平移2个单位,再向下平移1个单位,得到抛物线.
①求抛物线的解析式.
②设抛物线与轴交于,两点(点在点的右侧),与轴交于点,连接.点为第一象限内抛物线上一动点,过点作于点.设点的横坐标为.是否存在点,使得以点,,为顶点的三角形与相似,若存在,求出的值;若不存在,请说明理由.
参考答案
1.(1)证明:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
(2)证明:如图1所示:连接DE,交AF于点O.
∵四边形EFDG为菱形,
∴GF⊥DE,,
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴,即DF2=FO AF.
∵,
∴;
(3)如图2所示:过点G作GH⊥DC,垂足为H.
∵,
∴,整理得:FG2+3FG-10=0.
解得:FG=2,FG=-5(舍去).
∵
∴
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴,即,
∴.
∴.
2.(解:(1)∵AD∥BC,
∴,.
∵DB=DC=15,DE=DF=5,
∴,
∴,
∴BG=CH.
(2)过点D作DP⊥BC,过点N作NQ⊥AD,垂足分别为点P、Q.
∵DB=DC=15,BC=18,
∴BP=CP=9,DP=12.
∵,
∴BG=CH=2x,
∴BH=18+2x.
∵AD∥BC,
∴,
∴,
∴,
∴DN=.
∵AD∥BC,
∴∠ADN=∠DBC,
∴sin∠ADN=sin∠DBC,
∴,
∴NQ=.
∴y=AD NQ=x (0<x≤9).
(3)∵AD∥BC,
∴∠DAN=∠FHG.
(i)当∠ADN=∠FGH时,
∵∠ADN=∠DBC,
∴∠DBC=∠FGH,
∴BD∥FG,
∴,
∴,
∴BG=6,
∴AD=3.
(ii)当∠ADN=∠GFH时,
∵∠ADN=∠DBC=∠DCB,
又∵∠AND=∠FGH,
∴△ADN∽△FCG.
∴,
∴x (18 2x)= 10,整理得x2-3x-29=0,
解得x=,或x=(舍去).
综上所述,当△HFG与△ADN相似时,AD的长为3或.
3.(1)证明:如图1,连接OD,
∵BC是⊙O的切线,
∴∠ODB=90°=∠C,
∴ODAC,
∴∠ODA=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD,
∴AD平分∠BAC;
(2)证明:如图2,连接DF,EF.
∵AE是⊙O的直径,
∴∠AFE=90°=∠C.
∴EFBC,
∴∠B=∠AEF.
∵∠AEF=∠ADF,
∴∠B=∠ADF,
由(1)知∠BAD=∠DAF,
∴△ABD∽△ADF,
∴,
∴AD2=AB·AF;
(3)解:设⊙O的半径为R,则OA=OD=OE=R.
∵BE=8,
∴OB=BE+OE=8+R.
在Rt△BDO中,,
∴,
∴R=5,
∴AE=2OE=10,AB=BE+2OE=18,
由(2)知∠AEF=∠B,∠AFE=90°,
∴.
在Rt△AFE中,,
∴,
由(2)知AD2=AB·AF,
∴.
4.解:(1)设点的坐标为,则点的坐标为.
∵抛物线的对称轴为,
∴,∴,
∴点的坐标为,点的坐标为,
∴,抛物线的解析式为,顶点的坐标为
(2)设动点的坐标为,
①当∽时,,则,
∴,(舍去),
∴点的坐标为.
②当∽时,,则,
∴,(舍去),
∴点的坐标为.
∴动点的坐标为或.
5.解:(1)如图,∵,,,
∴,且,
∴,
∴,
∴
(2)如图2,连接BD,
∵,,
∴
在正方形ABCD中,,
∴,,
,
∴;
(3)如图,过点作,交于点,连接
又
即
6.证明:(1)作,垂足为,
∵四边形ABCD为正方形,
∴∠B=∠NAB=90°,∠NHB=90°,
∴∠B=∠NAB=∠NHB=90°,
∴四边形ABHN为矩形,
∴,
,
,又,
,
,
;
(2)①.
点与点关于直线对称,且四边形是正方形,
,,
,
在等腰中,,
又,
;
②.
证明:连接,,
由对称性可知,
即是等腰直角三角形,
∴FC,
,
∵四边形ABCD为正方形,
∴,
,
,
又,
,
,
.
7.解:(1)若,则,即四边形ABCD为正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∵∠EOF=90°,
∴∠EOB=∠FOC,
∴△OEB≌△OFC,
∴OE=OF,
∴
故答案为:1;
(2).
理由:过作于,作于,
∵,
∴四边形是矩形.
∴,
∴,
∵,
∴,
∵,
∴,
∴,
在矩形中,,
∵,
∴,
∴,
同理,
∴,
∴;
(3)∵,
∴,
由(2),,
∴,
∴,
∵,
∴,
∴,
令,则,
由题意,,
由勾股定理得,,
解得:,
∴,
∴,
∴,
由(2)知,,
∴在中,,
∴.
8.解:(1)如图:∵矩形中,
∴CD=AB=10,AD=BC=8
根据折叠的性质可得DC'=DC=10
在直角三角形ADC'中,AC'=.
(2)由折叠可知:.
在中,根据勾股定理可求得,
∴.
在中,设,根据勾股定理,得,
解得,即.
如图:连接,则由平移可知,,且.
于是可得,
∴,
又∵,
∴.
(3)四边形不是平行四边形,理由如下:
由折叠可知;
又∵平移可知,且,
∴,
∴,即是等腰三角形,
∴.
如图,过点作于点H,则且,
∴ .
设,则,
在中,根据勾股定理,得,
解得,
∴,
∴.
而在中,,
根据勾股定理可求得,
∴,即,
故四边形不可能是平行四边形.
9.(1)证明:∵四边形是菱形,,
∴ ,,
∴是等边三角形,
∴,,
∵
∴.
(2)①证明:连接,延长到点,使,连接.
由(1)知,
∴,
,,
∴,
∵是等边三角形,
∴,
∴,
∴,,
∴
∴是等边三角形,
∴.
②由①可知,
∵,∴,
又∵,
∴,
∴,
∴,即,
∴.
10.解:(1)如图,相似三角形有:,,.
证明如下:
∵,,
∴,,
又∵,,
∴,,
∴,
又∵,
∴;
(答案不唯一,选取一个说明即可)
(2)过P作,分别交BE、BC于点H、G
,.
,.是等腰直角三角形.
.
∵,,
.
∴,
,
.
∵,,.
∴.
在和中
,
∴,
∴,
∴;
(3)过点作,过点作,如下图:
设,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∵,
∴,,
∴,
在中,,即,
解得,,
又∵,
∴
,
∴.
11.解:(1)和均为等腰直角三角形,
,,,
,
,且,,
,
,
,
,
故答案为:;
②如图,过点作于点,
,,,
,
,
,
故答案为:4;
(2)若点在右侧,
如图,过点作于点,
,,,,.
,,
,
,
,,
,
,,
,
,
即,
,,
,
,
若点在左侧,
,,,,.
,,
,
,
,
,,
,
,,
,
,
即,
,,
,
.
12.解:(1)连接,如下图:
∵点D为BC边中点
∴
又∵为等腰直角三角形
∴,,
∴
又∵
∴
∴
∴
(2)分别过点、作、交于点
∵为等腰直角三角形
∴
又∵、
∴、为等腰直角三角形
∴,
∵,
∴
∴
∴
∴,,
∴,
∴
又∵
∴
∴,即
(3)∵,
∴
又∵
∴
∴
∴
设,
∴
∴当时,最大,最大为1.
13.(1)证明:如图,连接、,
∵,,
∴点都在线段的垂直平分线上,
∴是线段的垂直平分线,
∴;
(2)证明:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(3)解:如图,连接,
∵,,
∴是线段的垂直平分线,,
∴,
∵是线段的垂直平分线,
∴.
∵,
∴.
∵,,
∴,
∵,
∴,
∴.
设,则,
∴,
在中,,
∵,,
∴.
∵,,
∴,
∴,即,
∴,
整理得,
解得(不合题意,舍去),
∴,
∵,
∴.
14.解:(1)过点C作CE∥AB交BA的延长线于点E,
∴,∠DAC=∠ACE,∠BAD=∠E
∵AD是内角平分线,
∴∠BAD=∠DAC,
∴∠E=∠ACE,
∴AE=AC,
故;
(2)连接CE,
∵∠AEC=∠ABC,∠BAD=∠ECD,
∴△ABD∽△CED,
∴,即BD CD=AD DE,
同理可得:△ABD∽△AEC,故AB AC=AD AE,
即AB AC=AD(AD+DE)=AD2+AD ED=AD2+BC CD,
∴AD2=AB AC﹣BD CD;
(3)由(1)知,,
而BC=5,故BD=3,CD=2,
则AD2=AB AC﹣BD CD=24﹣6=18,
∴AD=3;
(4)由(1)知,,
∴BDAC,则BC,
∴AD2=AB AC﹣BD CD=bc,
∴AD,
故答案为.
15.(1)解:如图,连接OD,交BC于点N,
AB为直径
弦AD平分∠BAC,
四边形CNDM为矩形
OD为圆的半径
MD是⊙O的切线
(2)解:在点E运动过程中,EC+EM存在最小值,理由如下:
过点C作,并延长交⊙O于点F,连接MF,交AB于点E,连接EC,则此时EC+EM的值最小
弦AD平分∠BAC,
与的度数为
AB是直径
,AB是直径
为半圆
FD为圆的直径
由(1)知:MD是⊙O的切线
由题意得:AB垂直平分FC
由(1)知:四边形CNDM为矩形
在中
在中
EC+EM的最小值为.
(3)解:如图
FC平分,
AD平分,
解得或(不合题意,舍去)
16.解:(1)∵点为中斜边的中点,
∴,
∵线段绕点顺时针旋转得到线段,
∴,
∴,
∵中,,,
∴,
∵,
∴,
∴在中,,
故答案为:;;
(2)①正方形,理由如下:
∵,平分,
∴,,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
∴四边形为矩形,
又∵,
∴四边形为正方形;
②显然,在正方形中,,
∴,
又∵,
∴,
由(1)得:则为等边三角形,
∴,
∵,
∴,
∴,,
又∵,
∴,
∴,
∵,
∴
在与中,
∴,
∴,
∴;
(3)同(2)中①理,,
∴,,
∵,
∴,
∴,,
∴,,
∴四边形为菱形,
∵为等边三角形,
∴,菱形的边长也为2,
由题意,,,
∵,
∴,
即:,
∴,
∵在菱形中,,
∴,
∴,
如图,作,
∵,
∴,,
∵,
∴,,
在中,,
∴,
∴,
在中,,
∴,
∵,
∴.
17.解:(1)设CF交BE于点H,
∵四边形为矩形
∴,
∴
由翻折可得:,
∴为的中垂线
∴
∵,
∴
∴
∴
∴
由翻折得
∴
∴
故答案为:
(2)∵将沿BE翻折,使点C恰好落在AD边上点F处
∴,
又∵矩形ABCD中,
∴,
∴
∴
∴
∴
∵,
∴
∴
∴
∴
∴
(3)过点作于点
∵
∴
∵,
∴
∵,
∴
∴,设
∵平分,,
∴,,设,则
∵
∴
解得
∴
∴
18.解:(1)∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴.
∴的长为.
(2)∵,
∴,
∵,
∴,
∴,
∵,,,
∴,
∴,,
∵,
在中,,
∴.
故答案为:.
(3)如图,过点作交延长线于点,
∴,,
∴,
∴,
即:
∵,,
∴,,
∴,
∴,,
∴,
∵,
又∵,
∴,
∴,
即,
又∵,
在和中,
,
∴,
∴,
∴,
∵,,
∴.
故答案为:.
19.(1)解:∵,
∴,
∵四边形为矩形,
∴,,,
∴,
∴,
∴,
∴;
(2)解:构造如图所示矩形,延长交于点G,
由(1)中结论可得:,
∵,
∴设,,
∵点为的中点,
∴,
在中,根据勾股定理可得:,
∵,
∴,则,,
解得:,,
∵四边形为矩形,
∴,
∴,
∴,
∴,即,
解得:,
∴;
(3)解:连接,构造如图所示矩形,过点N作,交于点P,
∵,,,
∴,
∴,
∴,
∵四边形为矩形,
∴,
∴,
∵,
∴,
∵,
∴设,,
∴,
设,
则,,
∴,整理得:,
∴,
由(1)中结论可得:.
∵,,
∴四边形为平行四边形,
∴,
∴.
故答案为:.
20.解:(1)因为抛物线图像过(1,1)、(4,1)两点,
这两点的纵坐标相同,根据抛物线的性质可知,对称轴是x=(1+4)÷2=2.5,;
(2)①将点(1,1)、(4,1)向左平移2个单位,再向下平移1个单位,得到(-1,0),(2,0),将点(-1,0),(2,0),a=-1,
根据交点式可求出C1二次函数表达式为;
②根据①中的函数关系式,可得A(2,0),B(-1,0),C(0,2),D(m,),且m>0
由图像可知∠BOC=∠DEO=90°,
则以点,,为顶点的三角形与相似有两种情况,
(i)当△ODE∽△BCO时,
则,即,
解得m=1或-2(舍),
(ii)当△ODE∽△CBO时,
则,即,
解得
所以满足条件的m的值为1或.
1.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证EG2=GF AF;
(3)若AG=3,EG=,求BE的长.
2.如图,在梯形中,,,,点、分别在线段、上,.的延长线交边于点,交于点、其延长线交的延长线于点.
(1)求证:;
(2)设,的面积为,求关于的函数解析式,并写出它的定义域;
(3)联结,当与相似时,求的长.
3.如图,在中,,为上一点,经过点的分别交,于点,,与相切于点,连接,相交于点.
(1)求证:平分;
(2)求证:;
(3)若,,求的长.
4.如图,抛物线与轴交于、两点,与轴正半轴交于点,已知.
(1)求抛物线的解析式及顶点的坐标.
(2)若为第一象限抛物线上的一个动点,为轴上的一点,过点作轴,若与以点、、为顶点的三角形相似,求动点的坐标.
5.【问题背景】(1)如图1,,,.求证:;
【变式迁移】(2)如图2,E为正方形ABCD外一点,,过点D作,垂足为F,连接CF.求的值;
【拓展创新】(3)如图3,A是内一点,,,,,,直接写出AB的长.
6.如图,为正方形对角线上的一点,连接并延长交于点,过作分别交,于,.
(1)如图1,求证:;
(2)如图2,点与点关于直线对称,连接并延长交直线于点,连接.
①设的度数为,求的度数:
②猜想与之间的数量关系,并证明.
7.在矩形中,点是对角线、的交点,直角的顶点与重合,、分别与、边相交于、,连接,(为常数).
(1)发现问题:如图1,若,猜想:________;
(2)类比探究:如图2,,探究线段,之间的数量关系,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,若,,,求的长.
8.综合与实践
【问题背景】
如图1,矩形中,.点E为边上一点,沿直线将矩形折叠,使点C落在边的点处.
【问题解决】
(1)填空:的长为______.
(2)如图2,将沿线段向右平移,使点与点B重合,得到与交于点F,与交于点G.求的长;
【拓展探究】
(3)在图2中,连接,则四边形是平行四边形吗?若是,请予以证明;若不是,请说明理由.
9.在菱形中,,点、分别是边、上两点,满足,与相交于点.
(1)如图1,连接.求证:;
(2)如图2,连接.
①求证:;
②若,,求线段的长(用含、的代数式表示).
10.(1)如图1,,垂足为D,,垂足为E,AD与BE相交于点F,连接ED.你能在图中找出一对相似三角形,并说明相似的理由吗?
(2)如图2,在中,,,,重足为E,P为AB上一点,于D,交BE于F.求证:;
(3)如图3,在中,,M为AC上一点,连接BM,,,,请直接写出BC的长.
11.【问题探究】
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.
①请探究AD与BD之间的位置关系?并加以证明.
②若AC=BC=,DC=CE=,求线段AD的长.
【拓展延伸】
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
12.如图1,在等腰中,,点D为斜边AB边上一动点(不含端点).作,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题:
【问题发现】
(1)如图1,若点D为BC边中点.请直接写出DE,DF的数量关系_________.
【类比探究】
(2)如图2,若点D为BC边上一动点,且.猜想DF与DE的数量关系.并证明你的结论.
【拓展应用】
(3)如图3,在边长为4的等边中,点D为BC边上一动点,作.DE交AC边于点E.请问在点D的运动过程中,CE是否有最大值.如果有,求出最大值;如果没有,请说明理由.
13.如图1,已知:内接于圆O,,连接并延长,交于点D.
(1)求证:
(2)如图2,过点B作于点E,交圆O于点F,交于点G,求证:;
(3)如图3,在(2)的条件下,连接DE,,,求DE的长.
14.【问题提出】已知一个三角形的三条边长,怎样求出其内角平分线的长度?
【问题转化】
(1)已知:如图1,中,是内角平分线.求证:;
(2)已知:如图2,内接于,延长的内角平分线交于点.求证:;
【问题解决】
(3)已知:如图3,中,,,,是的内角平分线.求的长;
(4)已知:如图3,中,,,,是的内角平分线.请直接写出求的计算公式:__________.
15.如图,⊙O是△ABC的外接圆,AB为直径,弦AD平分∠BAC,过点D作射线AC的垂线,垂足为M,点E为线段AB上的动点.
(1)求证:MD是⊙O的切线;
(2)若∠B=30°,AB=8,在点E运动过程中,EC+EM是否存在最小值?若存在,请求出最小值;若不存在,说明理由;
(3)若点E恰好运动到∠ACB的角平分线上,连接CE并延长,交⊙O于点F,交AD于点P,连接AF,CP=3,EF=4,求AF的长.
16.如图,在中,,,点为的中点,连接,将线段绕点顺时针旋转得到线段,且交线段于点,的平分线交于点.
(1)如图1,若,则线段与的数量关系是________,________;
(2)如图2,在(1)的条件下,过点作交于点,连接,.
①试判断四边形的形状,并说明理由;
②求证:;
(3)如图3,若,,过点作交于点,连接,,请直接写出的值(用含的式子表示).
17.在矩形ABCD的CD边上取一点E,将沿BE翻折至的位置.
(1)如图1,当点F落在矩形ABCD内部时,连接CF并延长,交AD于点G,若,,,则GF的长度为________________;
(2)如图2,当点C恰好落在AD边上点F处时,若,且,求BC的长;
(3)如图3,当点C恰好落在AD边上点F处时,延长EF,与的角平分线交于点M,BM交AD于点N,当时,求的值.
18.【基础探究】(1)如图①,在中,为上一点,,交延长线于点,若,求的长.
【拓展延伸】(2)如图②,在中,为上一点,,交延长线于点,,, ,则 .
【拓展延伸】(3)如图③,点为四边形内部一点,且有,,于点,为上一点,,若,,则的面积为 .
19.【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形中,点,分别是边,上的点,连接,,且于点,若,,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
【初步运用】
(2)如图2,在中,,,点为的中点,连接,过点作于点,交于点,求的值.
【灵活运用】
(3)如图3,在四边形中,,,,,点,分别在边,上,且,垂足为,则__________________.
20.如图,在平面直角坐标系中,抛物线:经过点和.
(1)求抛物线的对称轴.
(2)当时,将抛物线向左平移2个单位,再向下平移1个单位,得到抛物线.
①求抛物线的解析式.
②设抛物线与轴交于,两点(点在点的右侧),与轴交于点,连接.点为第一象限内抛物线上一动点,过点作于点.设点的横坐标为.是否存在点,使得以点,,为顶点的三角形与相似,若存在,求出的值;若不存在,请说明理由.
参考答案
1.(1)证明:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
(2)证明:如图1所示:连接DE,交AF于点O.
∵四边形EFDG为菱形,
∴GF⊥DE,,
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴,即DF2=FO AF.
∵,
∴;
(3)如图2所示:过点G作GH⊥DC,垂足为H.
∵,
∴,整理得:FG2+3FG-10=0.
解得:FG=2,FG=-5(舍去).
∵
∴
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴,即,
∴.
∴.
2.(解:(1)∵AD∥BC,
∴,.
∵DB=DC=15,DE=DF=5,
∴,
∴,
∴BG=CH.
(2)过点D作DP⊥BC,过点N作NQ⊥AD,垂足分别为点P、Q.
∵DB=DC=15,BC=18,
∴BP=CP=9,DP=12.
∵,
∴BG=CH=2x,
∴BH=18+2x.
∵AD∥BC,
∴,
∴,
∴,
∴DN=.
∵AD∥BC,
∴∠ADN=∠DBC,
∴sin∠ADN=sin∠DBC,
∴,
∴NQ=.
∴y=AD NQ=x (0<x≤9).
(3)∵AD∥BC,
∴∠DAN=∠FHG.
(i)当∠ADN=∠FGH时,
∵∠ADN=∠DBC,
∴∠DBC=∠FGH,
∴BD∥FG,
∴,
∴,
∴BG=6,
∴AD=3.
(ii)当∠ADN=∠GFH时,
∵∠ADN=∠DBC=∠DCB,
又∵∠AND=∠FGH,
∴△ADN∽△FCG.
∴,
∴x (18 2x)= 10,整理得x2-3x-29=0,
解得x=,或x=(舍去).
综上所述,当△HFG与△ADN相似时,AD的长为3或.
3.(1)证明:如图1,连接OD,
∵BC是⊙O的切线,
∴∠ODB=90°=∠C,
∴ODAC,
∴∠ODA=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD,
∴AD平分∠BAC;
(2)证明:如图2,连接DF,EF.
∵AE是⊙O的直径,
∴∠AFE=90°=∠C.
∴EFBC,
∴∠B=∠AEF.
∵∠AEF=∠ADF,
∴∠B=∠ADF,
由(1)知∠BAD=∠DAF,
∴△ABD∽△ADF,
∴,
∴AD2=AB·AF;
(3)解:设⊙O的半径为R,则OA=OD=OE=R.
∵BE=8,
∴OB=BE+OE=8+R.
在Rt△BDO中,,
∴,
∴R=5,
∴AE=2OE=10,AB=BE+2OE=18,
由(2)知∠AEF=∠B,∠AFE=90°,
∴.
在Rt△AFE中,,
∴,
由(2)知AD2=AB·AF,
∴.
4.解:(1)设点的坐标为,则点的坐标为.
∵抛物线的对称轴为,
∴,∴,
∴点的坐标为,点的坐标为,
∴,抛物线的解析式为,顶点的坐标为
(2)设动点的坐标为,
①当∽时,,则,
∴,(舍去),
∴点的坐标为.
②当∽时,,则,
∴,(舍去),
∴点的坐标为.
∴动点的坐标为或.
5.解:(1)如图,∵,,,
∴,且,
∴,
∴,
∴
(2)如图2,连接BD,
∵,,
∴
在正方形ABCD中,,
∴,,
,
∴;
(3)如图,过点作,交于点,连接
又
即
6.证明:(1)作,垂足为,
∵四边形ABCD为正方形,
∴∠B=∠NAB=90°,∠NHB=90°,
∴∠B=∠NAB=∠NHB=90°,
∴四边形ABHN为矩形,
∴,
,
,又,
,
,
;
(2)①.
点与点关于直线对称,且四边形是正方形,
,,
,
在等腰中,,
又,
;
②.
证明:连接,,
由对称性可知,
即是等腰直角三角形,
∴FC,
,
∵四边形ABCD为正方形,
∴,
,
,
又,
,
,
.
7.解:(1)若,则,即四边形ABCD为正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∵∠EOF=90°,
∴∠EOB=∠FOC,
∴△OEB≌△OFC,
∴OE=OF,
∴
故答案为:1;
(2).
理由:过作于,作于,
∵,
∴四边形是矩形.
∴,
∴,
∵,
∴,
∵,
∴,
∴,
在矩形中,,
∵,
∴,
∴,
同理,
∴,
∴;
(3)∵,
∴,
由(2),,
∴,
∴,
∵,
∴,
∴,
令,则,
由题意,,
由勾股定理得,,
解得:,
∴,
∴,
∴,
由(2)知,,
∴在中,,
∴.
8.解:(1)如图:∵矩形中,
∴CD=AB=10,AD=BC=8
根据折叠的性质可得DC'=DC=10
在直角三角形ADC'中,AC'=.
(2)由折叠可知:.
在中,根据勾股定理可求得,
∴.
在中,设,根据勾股定理,得,
解得,即.
如图:连接,则由平移可知,,且.
于是可得,
∴,
又∵,
∴.
(3)四边形不是平行四边形,理由如下:
由折叠可知;
又∵平移可知,且,
∴,
∴,即是等腰三角形,
∴.
如图,过点作于点H,则且,
∴ .
设,则,
在中,根据勾股定理,得,
解得,
∴,
∴.
而在中,,
根据勾股定理可求得,
∴,即,
故四边形不可能是平行四边形.
9.(1)证明:∵四边形是菱形,,
∴ ,,
∴是等边三角形,
∴,,
∵
∴.
(2)①证明:连接,延长到点,使,连接.
由(1)知,
∴,
,,
∴,
∵是等边三角形,
∴,
∴,
∴,,
∴
∴是等边三角形,
∴.
②由①可知,
∵,∴,
又∵,
∴,
∴,
∴,即,
∴.
10.解:(1)如图,相似三角形有:,,.
证明如下:
∵,,
∴,,
又∵,,
∴,,
∴,
又∵,
∴;
(答案不唯一,选取一个说明即可)
(2)过P作,分别交BE、BC于点H、G
,.
,.是等腰直角三角形.
.
∵,,
.
∴,
,
.
∵,,.
∴.
在和中
,
∴,
∴,
∴;
(3)过点作,过点作,如下图:
设,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∵,
∴,,
∴,
在中,,即,
解得,,
又∵,
∴
,
∴.
11.解:(1)和均为等腰直角三角形,
,,,
,
,且,,
,
,
,
,
故答案为:;
②如图,过点作于点,
,,,
,
,
,
故答案为:4;
(2)若点在右侧,
如图,过点作于点,
,,,,.
,,
,
,
,,
,
,,
,
,
即,
,,
,
,
若点在左侧,
,,,,.
,,
,
,
,
,,
,
,,
,
,
即,
,,
,
.
12.解:(1)连接,如下图:
∵点D为BC边中点
∴
又∵为等腰直角三角形
∴,,
∴
又∵
∴
∴
∴
(2)分别过点、作、交于点
∵为等腰直角三角形
∴
又∵、
∴、为等腰直角三角形
∴,
∵,
∴
∴
∴
∴,,
∴,
∴
又∵
∴
∴,即
(3)∵,
∴
又∵
∴
∴
∴
设,
∴
∴当时,最大,最大为1.
13.(1)证明:如图,连接、,
∵,,
∴点都在线段的垂直平分线上,
∴是线段的垂直平分线,
∴;
(2)证明:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(3)解:如图,连接,
∵,,
∴是线段的垂直平分线,,
∴,
∵是线段的垂直平分线,
∴.
∵,
∴.
∵,,
∴,
∵,
∴,
∴.
设,则,
∴,
在中,,
∵,,
∴.
∵,,
∴,
∴,即,
∴,
整理得,
解得(不合题意,舍去),
∴,
∵,
∴.
14.解:(1)过点C作CE∥AB交BA的延长线于点E,
∴,∠DAC=∠ACE,∠BAD=∠E
∵AD是内角平分线,
∴∠BAD=∠DAC,
∴∠E=∠ACE,
∴AE=AC,
故;
(2)连接CE,
∵∠AEC=∠ABC,∠BAD=∠ECD,
∴△ABD∽△CED,
∴,即BD CD=AD DE,
同理可得:△ABD∽△AEC,故AB AC=AD AE,
即AB AC=AD(AD+DE)=AD2+AD ED=AD2+BC CD,
∴AD2=AB AC﹣BD CD;
(3)由(1)知,,
而BC=5,故BD=3,CD=2,
则AD2=AB AC﹣BD CD=24﹣6=18,
∴AD=3;
(4)由(1)知,,
∴BDAC,则BC,
∴AD2=AB AC﹣BD CD=bc,
∴AD,
故答案为.
15.(1)解:如图,连接OD,交BC于点N,
AB为直径
弦AD平分∠BAC,
四边形CNDM为矩形
OD为圆的半径
MD是⊙O的切线
(2)解:在点E运动过程中,EC+EM存在最小值,理由如下:
过点C作,并延长交⊙O于点F,连接MF,交AB于点E,连接EC,则此时EC+EM的值最小
弦AD平分∠BAC,
与的度数为
AB是直径
,AB是直径
为半圆
FD为圆的直径
由(1)知:MD是⊙O的切线
由题意得:AB垂直平分FC
由(1)知:四边形CNDM为矩形
在中
在中
EC+EM的最小值为.
(3)解:如图
FC平分,
AD平分,
解得或(不合题意,舍去)
16.解:(1)∵点为中斜边的中点,
∴,
∵线段绕点顺时针旋转得到线段,
∴,
∴,
∵中,,,
∴,
∵,
∴,
∴在中,,
故答案为:;;
(2)①正方形,理由如下:
∵,平分,
∴,,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
∴四边形为矩形,
又∵,
∴四边形为正方形;
②显然,在正方形中,,
∴,
又∵,
∴,
由(1)得:则为等边三角形,
∴,
∵,
∴,
∴,,
又∵,
∴,
∴,
∵,
∴
在与中,
∴,
∴,
∴;
(3)同(2)中①理,,
∴,,
∵,
∴,
∴,,
∴,,
∴四边形为菱形,
∵为等边三角形,
∴,菱形的边长也为2,
由题意,,,
∵,
∴,
即:,
∴,
∵在菱形中,,
∴,
∴,
如图,作,
∵,
∴,,
∵,
∴,,
在中,,
∴,
∴,
在中,,
∴,
∵,
∴.
17.解:(1)设CF交BE于点H,
∵四边形为矩形
∴,
∴
由翻折可得:,
∴为的中垂线
∴
∵,
∴
∴
∴
∴
由翻折得
∴
∴
故答案为:
(2)∵将沿BE翻折,使点C恰好落在AD边上点F处
∴,
又∵矩形ABCD中,
∴,
∴
∴
∴
∴
∵,
∴
∴
∴
∴
∴
(3)过点作于点
∵
∴
∵,
∴
∵,
∴
∴,设
∵平分,,
∴,,设,则
∵
∴
解得
∴
∴
18.解:(1)∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴.
∴的长为.
(2)∵,
∴,
∵,
∴,
∴,
∵,,,
∴,
∴,,
∵,
在中,,
∴.
故答案为:.
(3)如图,过点作交延长线于点,
∴,,
∴,
∴,
即:
∵,,
∴,,
∴,
∴,,
∴,
∵,
又∵,
∴,
∴,
即,
又∵,
在和中,
,
∴,
∴,
∴,
∵,,
∴.
故答案为:.
19.(1)解:∵,
∴,
∵四边形为矩形,
∴,,,
∴,
∴,
∴,
∴;
(2)解:构造如图所示矩形,延长交于点G,
由(1)中结论可得:,
∵,
∴设,,
∵点为的中点,
∴,
在中,根据勾股定理可得:,
∵,
∴,则,,
解得:,,
∵四边形为矩形,
∴,
∴,
∴,
∴,即,
解得:,
∴;
(3)解:连接,构造如图所示矩形,过点N作,交于点P,
∵,,,
∴,
∴,
∴,
∵四边形为矩形,
∴,
∴,
∵,
∴,
∵,
∴设,,
∴,
设,
则,,
∴,整理得:,
∴,
由(1)中结论可得:.
∵,,
∴四边形为平行四边形,
∴,
∴.
故答案为:.
20.解:(1)因为抛物线图像过(1,1)、(4,1)两点,
这两点的纵坐标相同,根据抛物线的性质可知,对称轴是x=(1+4)÷2=2.5,;
(2)①将点(1,1)、(4,1)向左平移2个单位,再向下平移1个单位,得到(-1,0),(2,0),将点(-1,0),(2,0),a=-1,
根据交点式可求出C1二次函数表达式为;
②根据①中的函数关系式,可得A(2,0),B(-1,0),C(0,2),D(m,),且m>0
由图像可知∠BOC=∠DEO=90°,
则以点,,为顶点的三角形与相似有两种情况,
(i)当△ODE∽△BCO时,
则,即,
解得m=1或-2(舍),
(ii)当△ODE∽△CBO时,
则,即,
解得
所以满足条件的m的值为1或.
同课章节目录
