2024年 九年级数学中考复习 二次函数与平行四边形综合压轴题 专题提升训练(含答案)
文档属性
| 名称 | 2024年 九年级数学中考复习 二次函数与平行四边形综合压轴题 专题提升训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 00:00:00 | ||
图片预览


文档简介
2024年春九年级数学中考复习《二次函数与平行四边形综合压轴题》
专题提升训练(附答案)
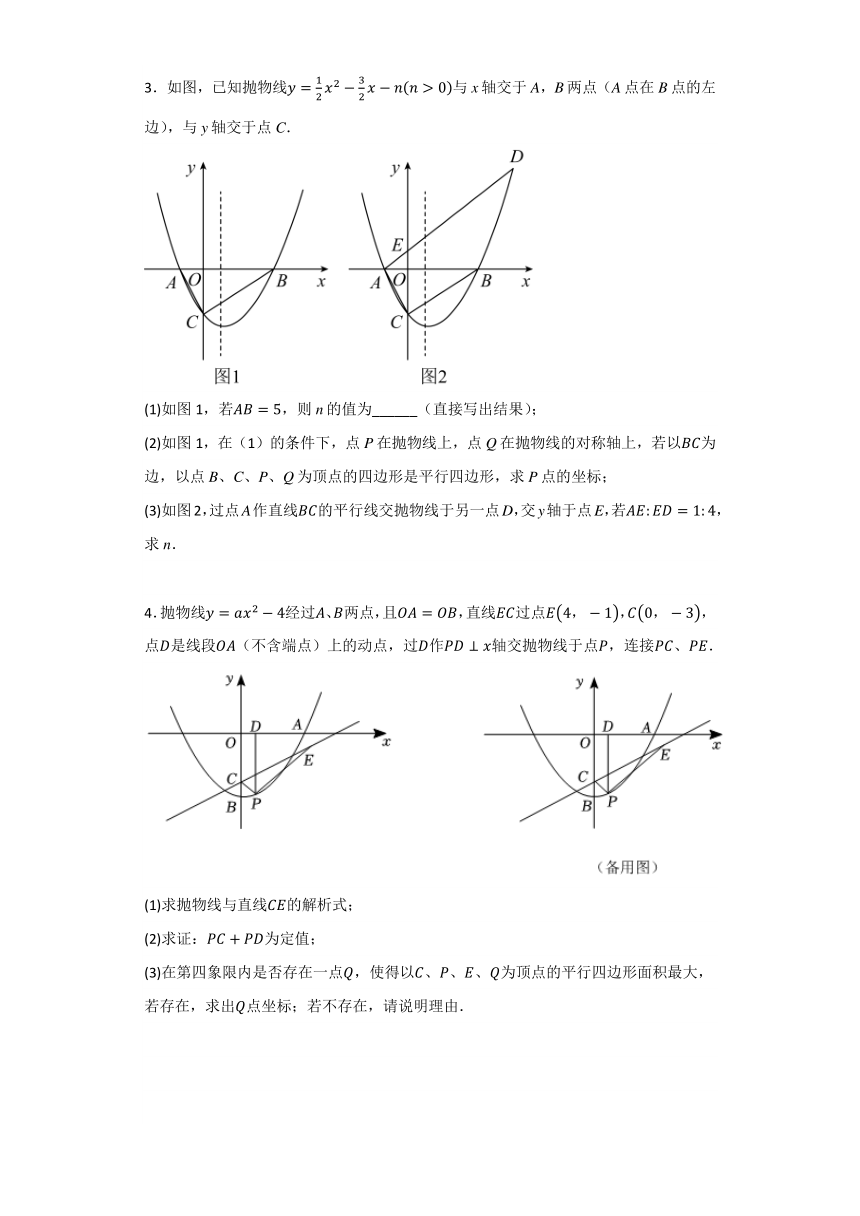
1.如图,已知抛物线与轴交于点,与轴交于,两点,点在点左侧,点的坐标为,
(1)求抛物线的函数关系式;
(2)若点是轴上的一点,在抛物线上是否存在点,使以,,,为顶点且以为一边的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
2.如图,在平面直角坐标系中,已知抛物线与x轴交于,两点,与y轴交于点C,连接.
(1)求该抛物线的解析式;
(2)点P为直线上方的抛物线上一点,过点P作y轴的垂线交线段于M,过点P作x轴的垂线交线段于N,求的周长的最大值.
(3)若点N为抛物线对称轴上一点,抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请求出所有满足条件的点M的坐标;若不存在,请说明理由.
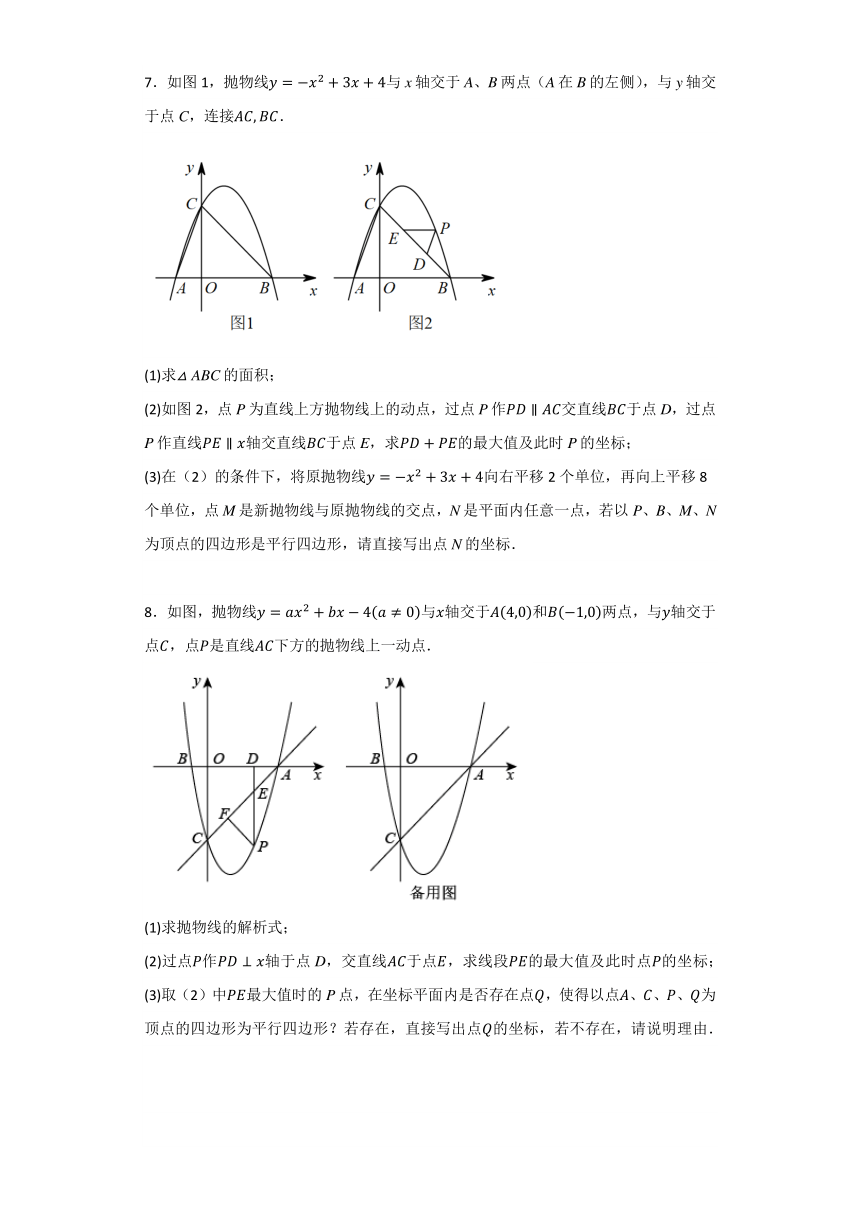
3.如图,已知抛物线与x轴交于A,B两点(A点在B点的左边),与y轴交于点C.
(1)如图1,若,则n的值为______(直接写出结果);
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以为边,以点B、C、P、Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线的平行线交抛物线于另一点D,交y轴于点E,若,求n.
4.抛物线经过、两点,且,直线过点,,点是线段(不含端点)上的动点,过作轴交抛物线于点,连接、.
(1)求抛物线与直线的解析式;
(2)求证:为定值;
(3)在第四象限内是否存在一点,使得以、、、为顶点的平行四边形面积最大,若存在,求出点坐标;若不存在,请说明理由.
5.如图1,抛物线与x轴交于A,B.两点(点A在点B的左边),与y轴交于点C,直线经过点A,C.
(1)求直线的解析式;
(2)点P为直线上方抛物线上的一个动点,过点P作于点D,过点P作交x轴于点E,求的最大值及此时点P的坐标;
(3)在(2)问取得最大值的情况下,将该抛物线沿射线方向平移个单位后得到新抛物线,点M为新抛物线对称轴上一点,在新抛物线上确定一点N,使得以点P,C,M,N为顶点的四边形是平行四边形,写出所有符合条件的点M的坐标,并写出求解点M的坐标的其中一种情况的过程.
6.在平面直角坐标系中,抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为.
(1)求点C的坐标;
(2)如图1,若点P是第二象限内抛物线上一动点,求点P到直线距离的最大值,并求出此时点P的坐标;
(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
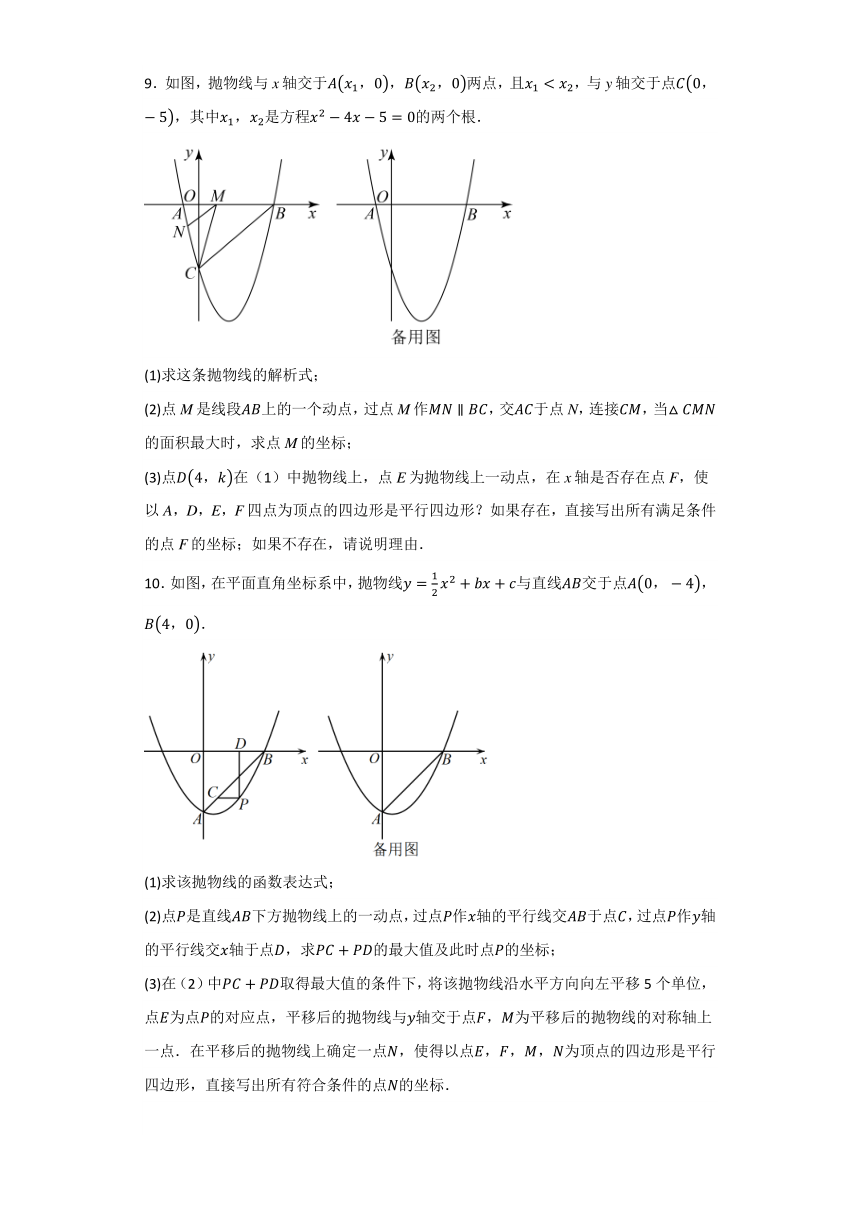
7.如图1,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C,连接.
(1)求△ABC的面积;
(2)如图2,点P为直线上方抛物线上的动点,过点P作交直线于点D,过点P作直线轴交直线于点E,求的最大值及此时P的坐标;
(3)在(2)的条件下,将原抛物线向右平移2个单位,再向上平移8个单位,点M是新抛物线与原抛物线的交点,N是平面内任意一点,若以P、B、M、N为顶点的四边形是平行四边形,请直接写出点N的坐标.
8.如图,抛物线与轴交于和两点,与轴交于点,点是直线下方的抛物线上一动点.
(1)求抛物线的解析式;
(2)过点作轴于点D,交直线于点,求线段的最大值及此时点的坐标;
(3)取(2)中最大值时的P点,在坐标平面内是否存在点,使得以点、、、为顶点的四边形为平行四边形?若存在,直接写出点的坐标,若不存在,请说明理由.
9.如图,抛物线与x轴交于两点,且,与y轴交于点,其中是方程的两个根.
(1)求这条抛物线的解析式;
(2)点M是线段上的一个动点,过点M作,交于点N,连接,当的面积最大时,求点M的坐标;
(3)点在(1)中抛物线上,点E为抛物线上一动点,在x轴是否存在点F,使以A,D,E,F四点为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;如果不存在,请说明理由.
10.如图,在平面直角坐标系中,抛物线与直线交于点,.
(1)求该抛物线的函数表达式;
(2)点是直线下方抛物线上的一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,求的最大值及此时点的坐标;
(3)在(2)中取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点为点的对应点,平移后的抛物线与轴交于点,为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点,使得以点,,,为顶点的四边形是平行四边形,直接写出所有符合条件的点的坐标.
11.如图,已知抛物线与一直线相交于,两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线的解析式.
(2)设点,求使的值最小时m的值.
(3)若抛物线的对称轴与直线相交于点B,E为直线上的任意一点,过E作交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求出点E,F的坐标;若不能,请说明理由.
12.综合与探究
如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,抛物线)经过,两点,与轴相交于另一点,连接.点是线段上方抛物线上的一个动点,过点作交线段于点.
(1)求抛物线的解析式;
(2)点为抛物线对称轴上的一个动点,则的最大值是___________;
(3)求的最大值,并写出此时点的坐标;
(4)在轴上找一点,抛物线上找一点,使以点为顶点的四边形是平行四边形,请直接写出点的坐标.
13.如图1,在平面直角坐标系中,抛物线与轴交于点,点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)点P为直线上方抛物线上的一点,过点P作x轴的平行线交于点D,过点P作y轴的平行线交于点E,求的最大值以及此时点P的坐标;
(3)如图2,将抛物线沿射线的方向平移,使得平移后的抛物线经过线段的中点,且平移后抛物线的对称轴与x轴交于点M,N,R是直线BC上任意两点,Q为新抛物线上一点,直接写出所有使得以点M,N,R,Q为顶点的四边形是平行四边形的点Q的横坐标,并把求其中一个点的横坐标过程写出来.
14.抛物线()与x轴交于点,两点,与y轴交于点,点P是抛物线上的一个动点.
(1)求抛物线的函数表达式;
(2)如图1,点P在线段上方的抛物线上运动(不与A,C重合),过点P作,垂足为D,交于点E.作,垂足为F,若点P的横坐标为t,请用t的式子表示,并求的面积的最大值;
(3)如图2,点Q是抛物线的对称轴l上的一个动点,在抛物线上存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形,请直接写出所有符合条件的点P的坐标,并把求其中一个点P的坐标的过程写下来.
15.综合与探究
如图1,在平面直角坐标系中,二次函数的图象与x轴交于A,B两点,与直线l交于B,C两点,其中点A的坐标为,点C的坐标为.
(1)求二次函数的表达式和点B的坐标.
(2)若P为直线l上一点,Q为抛物线上一点,当四边形为平行四边形时,求点P的坐标.
(3)如图2,若抛物线与y轴交于点D,连接,抛物线上是否存在点M,使?若存在,请直接写出点M的坐标;若不存在,请说明理由.
16.在直角坐标系中,抛物线与x轴交于A、B两点.其中点,点.
(1)求抛物线的解析式.
(2)如图1,在直线经过点,与轴交于.在直线l下方的抛物线上有一个动点,连接,,求面积的最大值及其此时的坐标.
(3)将抛物线y向右平移个单位长度后得到新抛物线,点是新抛物线的对称轴上的一个动点,点是原抛物线上的一个动点,取面积最大值时的点.若以点、、、为顶点的四边形是平行四边形,直接写出点的坐标,并写出求解其中一个点的过程.
17.如图,已知抛物线的顶点为点,且与轴交于,两点(在的左侧),与轴交于点.点为抛物线对称轴上的一个动点:
(1)当点在轴上方且时,求的值;
(2)若点在抛物线上,是否存在以点,,,为顶点的四边形是平行四边形﹖请求出点的坐标;
(3)若抛物线对称轴上有点,使得取得最小值,连接并延长交第二象限抛物线为点,请直接写出的长度.
18.图1,在平面直角坐标系中,已知抛物线经过,两点.P是抛物线上一点,且在直线的上方.
(1)求抛物线的解析式;
(2)如图2,点E为中点,作轴交于点Q,若四边形为平行四边形,求点P的横坐标;
(3)如图3,连结,交于点M,作交于点H.记,,的面积分别为.判断是否存在最大值,若存在,求出最大值;若不存在,请说明理由.
19.如图,在平面直角坐标系中,抛物线与x轴交于两点(点A在点B的左侧),与y轴交于点C,连接,点P为直线上方抛物线上一动点,连接交于点Q.
(1)求抛物线的函数表达式;
(2)当的值最大时,求点P的坐标和的最大值;
(3)把抛物线向右平移1个单位,再向上平移2个单位得新抛物线,M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,写出所有符合条件的N点的坐标,并写出求解点N的坐标的其中一种情况的过程.
20.抛物线与x轴交于,与y轴交于点.
(1)求抛物线的表达式;
(2)如图1,M为抛物线对称轴l上一动点,连接,求的最小值及此时M点的坐标;
(3)如图2,抛物线的对称轴l与x轴交于点E,点,P为抛物线上一动点,Q为抛物线对称轴l上一动点,以点E、F、P、Q为顶点的四边形为平行四边形时,直接写出所有可能的点Q的坐标.
参考答案
1.(1)解:∵点的坐标为,
∴,
∵,
∴,
∴,
∵抛物线过点,
∴
解得
∴抛物线的函数关系式为;
(2)在抛物线上存在点,使以,,,为顶点且以为一边的四边形是平行四边形;
理由:①如图1,当点在轴下方时,则:,
∴点的纵坐标为,
令,则,
解得,,
∴点的坐标为;
②如图2,当点在轴上方时,
∵平行四边形的对角线分平行四边形为面积相等的两个三角形,点到轴的距离为3,
∴点到轴的距离为3,
令,则,
解得,
∴,,
综上可得,在抛物线上存在点,使以,,,为顶点且以为一边的四边形是平行四边形,点的坐标为或或.
2.(1)解:(1)抛物线过,两点,
,
解得,
抛物线的解析式为;
(2)当时,,即:,
则,,,
设的解析式为:,将,代入可得:
,解得:,
∴的解析式为:,
设,
∵点P为直线上方的抛物线上一点,过点P作y轴的垂线交线段于M,过点P作x轴的垂线交线段于N,
∴,则,
当时,点的纵坐标为:,
则 ,
∴当时,有最大值为:,
由题意可知,,轴,则,
∴,
则,则,,
的周长为,
则当最大时,的周长有最大值,
即:的周长的最大值为;
(3)存在点,使得以B,C,M,N为顶点的四边形是平行四边形,
①以为对角线,过C作轴交抛物线与M,点N在x轴上,,;
②以为边,过M作垂直抛物线对称轴于G,当,且时,四边形为平行四边形,M点横坐标,纵坐标,;
③过N作轴,与过M作轴交于H,当,时,四边形为平行四边形,M点横坐标为,纵坐标,;
综上所述:点的坐标为或或.
3.(1)解:∵抛物线与x轴交于A,B两点,
∴,,
∵,即,
∴
,
解得:;
(2)由(1)当时,
解得,,
,,
,,
抛物线对称轴为直线,
设点坐标为,,
由平行四边形性质可知,
当、为平行四边形对角线时,点坐标为,,
代入,
解得则点坐标为,,
当、为为平行四边形对角线时,点坐标为,,
代入,
解得则坐标为,,
综上点坐标为,,;
(3)设点坐标为,
,
则,,
,
,
,
,
,
由一元二次方程根与系数关系,
,
,
将点,,代入,
,
解得或(舍去),
则.
4.(1)解:令,则,
∴,
∵,
∴,
∴,
将点代入得:,
解得:,
∴抛物线的解析式为:;
设直线为,
将点,的坐标代入得,
,解得:,
∴直线的解析式是:;
(2)证明:设点,,如图,过点作轴于点,
则,则,,,
∴为定值;
(3)解:存在,理由:
①当是平行四边形的边时,
如下图:设直线交轴于点,交于点,
令,则,解得;
令,则,
∴,,则,
∴,,
过点作于点,则,
则,
则以、、、为顶点的平行四边形面积,
其中为常数,
故当最大时,平行四边形的面积最大,
设点,则点,
则,
即的最大值为,此时点;
②当是平行四边形的对角线时,如下图,
同理可得:以、、、为顶点的平行四边形面积,
此时,
∵当时,的值随最大而增大,而,
当时,最大值为,
故该种情况,不符合题设要求,
综上,点,即四边形为平行四边形时,符合题设要求,
设点,
由中点坐标公式得:,
解得:,
故点.
5.(1)解:当时,,
∴点,
当时,,
解得:,
∴点,
设直线的解析式为,
把点,代入得:
,解得:,
∴直线的解析式为;
(2)解:如图,过点P作轴于点F交于点G,
∵,,
∴,
∴,
设点,则点,
∴,,,
∵,
∴,
∵,
∴,
∴,即,
解得:,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,即,
解得:,
∴,
∴当时,有最大值,最大值为;此时点;
(3)解:∵,
∴原抛物线的顶点坐标为,
∵将该抛物线沿射线方向平移个单位后得到新抛物线,
∴相当于原抛物线沿x轴向右平移个单位,再沿y轴向上平移个单位后得到新抛物线,
∴新抛物线的解析式为,
∴新抛物线的对称轴为直线,
设点,,
若以对角线为对角线,有
,解得:,
此时点M的坐标为;
若以对角线为对角线,有
,解得:,
此时点M的坐标为;
若以对角线为对角线,有
,解得:,
此时点M的坐标为;
综上所述,点M的坐标为或或.
6.(1)解:将点代入得:,
解得:,
∴抛物线的表达式为:,
把代入得:,
∴点C的坐标为;
(2)解:过点P作轴于点D,交于点F,过点P作于点E,
∵,,
∴,
∴,
∵,轴,
∴,
∵,
∴,
∴,
在中,,
设直线的函数表达式为:,
将点,代入得:
,解得:,
∴直线的函数表达式为:,
设点,则,
∴,
∴当时,有最大值,最大值为,
∴.
把代入得:,
∴,
综上:点P到直线距离为,此时;
(3)解:由(1)可得,抛物线的表达式为:,
∴该抛物线是对称轴为直线,
∵点N再抛物线对称轴上,点M在抛物线上,
∴设点,,
①当为平行四边形的对角线时,
∵,,
∴中点为,
∵,,
∴,解得:,
∴,
∴;
②当为平行四边形的对角线时,
∵,,
∴中点为,
∵,,
∴,解得:,
∴,
∴
③当为平行四边形的对角线时,
∵,,
∴中点为,
∵,,
∴,解得:,
∴,
∴
综上:点M的坐标为或或.
7.(1)解:令,则,
解得或4,
∴,
∴,
令,则,
∴,
∴,
∴;
(2)解:∵,,
∴,
∵轴,
∴,
∵,
∴,
∴,
∴,即,
∴,
设直线的解析式为,
∴,解得,
∴直线的解析式为,
设,则,
∴,
∴,
∴当时,的值最大,最大值为,
此时;
(3)解:∵原抛物线向右平移2个单位,再向上平移8个单位得到新抛物线,
∴平移后的抛物线的解析式为,
联立方程组,解得,
∴,
设,
①当为平行四边形的对角线时,
,解得,
∴;
②当为平行四边形的对角线时,
,解得,
∴);
③当为平行四边形的对角线时,
,解得,
∴;
综上所述:N点坐标为或或.
8.(1)解:把,代入得:
解得,
抛物线的函数表达式为;
(2)由题意可得,则,
由题意可得直线过点、,则
设函数解析式为:,
依题意得:
解得:
的函数关系式为,
令,则,
∴当时,的最大值为4.
∴;
(3)存在.点的坐标为或或.
解:设,又、、,
当、为平行四边形的对角线时,与的中点重合,
∴,
解得:,
∴;
当、为平行四边形的对角线时,与的中点重合,
∴,
解得:,
∴;
当、为平行四边形的对角线时,与的中点重合,
∴,
解得:,
∴;
综上所述,点的坐标为或或.
9.(1)解:解方程得,则,
设抛物线解析式为,
把代入得,
解得,
∴抛物线解析式为;
(2)解:作轴于H,如图1,
设,
,
,
,即,
,
,
当时,的面积最大,此时M点的坐标为;
(3)解:当时,,则,
如图2,当,则,
∴,
∴此时F点坐标为或;
当 时,则点E和点D的纵坐标互为相反数,即点E的纵坐标为5,
当时,,
解得,
若E点坐标为,由于点向右平移5个单位,向下平移5个单位得到D点,则E点向右平移5个单位,向下平移5个单位得到F点,此时F点坐标为;
若E点坐标为,同样方法得到此时F点坐标为;
总上所述,满足条件的F点坐标为或或或.
10.(1)解:将点,代入得:,
解得:,
∴该抛物线的函数表达式为:;
(2)解:如图,设交于H,
∵,,
∴,
∴,
∵,,
∴,,
∴,
设直线的解析式为,
则,解得:,
∴直线的解析式为,
设,则,,
∴
,
∴当时,取得最大值,此时;
(3)解:由题意得:平移后抛物线解析式为,,
∴,
∵抛物线的对称轴为,
∴设,,
分情况讨论:
①当为对角线时,
则,
解得:,此时,
∴点N的坐标为;
②当为对角线时,
则,即,
此时,
∴点N的坐标为;
③当为对角线时,
则,即,
此时,
∴点N的坐标为,
综上所述,点N的坐标为或或.
11.(1)解;将,两点代入得,,
解得,
∴,
设直线的解析式为,
将,两点代入得,,
解得,
∴,
∴抛物线的解析式为,直线的解析式为;
(2)解:当,,
当,,
当,或,
∴,,抛物线与 轴的另一个交点坐标为,
∵,
如图,作直线平行于轴,则在直线上,作关于直线的对称点,连接,与直线交点为,连接,
由题意知,,,
∴,
∴当三点共线时,的值最小且为,
设直线的解析式为,
将点坐标代入得,
解得,
∴直线的解析式为,
将代入得,,
∴的值为;
(3)解:将代入得,,
∴,,
设,则,
∵以B,D,E,F为顶点的四边形为平行四边形,
∴,
∴,
①当,解得,(与重合,舍去),
∴,则,,
②当,解得,,
∴,则,,
,则,,
综上所述,以B,D,E,F为顶点的四边形能为平行四边形,,或,或,.
12.(1)解:∵直线与轴交于点,与轴交于点,
∴,,
∵抛物线)经过,两点,
∴,
解得,
∴抛物线的解析式为:,
(2)解:取关于对称轴的对称点,对称轴,
∴,
解方程得到,
∴,
∵,
∴当共线时,有最大值,
∴,
∴故答案为:;
(3)解:过点做轴交于点,
设直线的解析式为:,
∵,
∴,
∴直线的解析式为,
设,则,
∴,
∴当时,有最大值,
∴,
∵轴,
∴,
∵,
∴,
∴,
∴当最大时,最大,
∴此时;
(4)解:①为对角线,
∵,在轴上,
∴轴,为的对称点,
∴,,
∴,
∴,
②为边,为对角线,设,,
∴,
∴或(舍去),
∴,
∴,
③为边,为对角线,设,,
∴,
∴,
∴,
∴或,
综上可得到:、、、.
13.(1)解:将,点代入,
得,
解得,
该抛物线的解析式为;
(2)解: ,
,
轴,
.
又由题知是直角三角形,,
,
,
当最大时,的长最大,
设直线的解析式为:,
直线经过点,,
代入得:,
解得,
,
设,则,
,
,
当时,有最大值,,
,此时;
(3)解:由(2)得,,
∴中点的坐标为,
∴可以看作点C向右移动个单位长度,向下移动个单位长度,
∵抛物线经过点C,平移后的抛物线经过中点,
∵
∴平移后的抛物线的解析式为:,
对称轴为,
∴与x轴的交点坐标为,
设点Q的坐标为:
当为平行四边形的对角线时,如图所示:
对角线的交点仍在直线上,
∴的中点为,代入直线解析式得:
,
解得:,;
当为平行四边形的边时,,
设直线的解析式为,且,
将点代入得,
解得:,
∴直线的解析式为,
将点Q代入得: ,
解得:,
综上可得:点的横坐标为:或或或.
14.(1)解:将,,三点代入解析式得,
,
解得:,,,
∴;
(2)解:设解析式为,
将, 代入解析式可得,
,
解得:,
∴,
∵点P的横坐标为t,
∴,
∵,
∴,
∴,
∵, ,
∴,
∵,,
∴,
∴是等腰直角三角形,
过F作,
∵,
∴,
∴,
∴当时,面积最大,
;
(3)解:由(1)得,
,
设,
∵点A,P,C,Q为顶点的四边形是平行四边形,
①当为对角线时,
P点坐标为,
∴,
解得:,
;
②当为对角线时,
P点坐标为,
∴,
解得:,
;
③当为对角线时,
P点坐标为,
∴,
解得:,
;
综上所述:,,;
15.(1)解:∵点A的坐标为,点C的坐标为,
∴,解得:,
∴二次函数的表达式为;
令,则,
解得:,
∴点B的坐标为;
(2)解:如图,
∵点B的坐标为,
∴,
设直线l的解析式为,
把点,代入得:
,解得:,
∴直线l的解析式为,
∵四边形为平行四边形,
∴,
∴轴,
设点P的坐标为,则点Q的坐标为,
∴,
∴,
解得:或0(舍去),
∴点P的坐标为;
(3)解:对于,
令,,
∴点D的坐标为,
∴,
∵点,
∴,,
如图,过点A作于点E,
∵,
∴,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
过点M作轴于点F,
∴是等腰直角三角形,
∴,
设点M的坐标为,
∴,
∴,
解得:(舍去)或2或4,
∴点M的坐标为或.
16.解:(1)∵抛物线与x轴交于、两点.其中点,点
∴
(2)将代入,
得:
解得:
∴
令,解得:,
∴,
如图所示,过点作轴交于点,
设,则,
∴ ,
∴
,
∴对称轴为,且,
∴面积最大值为,
此时,;
(3)∵点,点关于对称,
则抛物线的对称轴为直线,
∵将抛物线y向右平移1个单位长度后得到新抛物线,
∴则平移后新抛物线的对称轴为直线,
设,,
①若以为对角线时,
,
解得:,
∴,
②为对角线时,
,
解得:,当时,,
∴,
③若以为对角线时,
,
解得:,当时,,
∴,
综上所述,或或.
17.(1)解:∵,
令,解得,,
即,,
把代入中,
得,
即,
∵,
∴对称轴是直线,
顶点,
设对称轴与x轴交于点F,
∴,,,
∵,
∴,
在,.
(2)解:存在
∵点在抛物线上,点在对称轴上,
∴可设,,,
①以为对角线时,由平行四边形的对角线互相平分;则,
∴,
解得,即;
同理②以为对角线时,,
解得,即;
③以为对角线时,,
解得,即;
综上所述,存在,,,使得点,,,为顶点的四边形是平行四边形;
(3)解:如图所示,过点作于点,交对称轴于点,连接并延长交第二象限抛物线为点,
在中,,
∴,
∴,
∴要取得最小值,即要最小,
∴当点,,三点共线且垂直时最小,
此时最小,
在,中,,
∴,
∴,即,
∵,
设直线的解析式为:,
则,
解得:,
∴的解析式为:,
联立,
解得或(舍去)
∴,
∴.
18.解:(1)∵抛物线经过,,
∴,
解得,
∴,
(2)当时,,
∴点C的坐标是,
∴,
∵四边形为平行四边形,E为中点,
∴,
设直线的解析式为,
则,
∴直线的解析式为,
设,
∴,
,
,
∴点P的横坐标为;
(3)∵,
∴,
,
作交y轴于N,作轴交于Q,
∴, ,
∴,
∴,,
∵,,
∴,
∴,
设,则,
∴,
.
∴最大值.
即存在最大值,最大值为.
19.(1)解:抛物线与x轴交于、两点(点A在点B的左侧),
,
解得:,
抛物线的函数表达式为;
(2)解:抛物线与y轴交于点C,
,
,
设直线的解析式为,把,代入,得:
,
解得:,
直线的解析式为,
如图1,过点P作轴交于点D,
设,则,
,
,
,
,
当时,取得最大值,此时,;
(3)解:∵向右平移1个单位,再向上平移2个单位得新抛物线,
新抛物线解析式为,对称轴为直线,
设,,
①当为的边时,
则,,
,
解得:,
;
②当为的边时,
则,,
,
解得:,
;
③当为的对角线时,
则,
解得:,
;
综上所述,N点的坐标为: 或或.
20.(1)解:将代入得,,
解得,,
∴抛物线的表达式为;
(2)解:如图1,连接,交于,连接,
由题意知,抛物线的对称轴为直线,,
∴当三点共线时,,此时值最小,
当时,,
∴,
在中,由勾股定理得,
∴值最小为;
设直线的解析式为,
将,代入得,,
解得,,
∴直线的解析式为,
当时,,
∴,
∴的最小值为,;
(3)解:设,以点E、F、P、Q为顶点的四边形为平行四边形时,分两种情况求解:
①为平行四边形的边;
如图2,四边形为平行四边形,
∴,,
∴,,
∴;
如图3,四边形为平行四边形,
∴的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
②为平行四边形的对角线;
如图4,四边形为平行四边形,
的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
综上所述,以点E、F、P、Q为顶点的四边形为平行四边形时,所有可能的点Q的坐标为,,.
专题提升训练(附答案)
1.如图,已知抛物线与轴交于点,与轴交于,两点,点在点左侧,点的坐标为,
(1)求抛物线的函数关系式;
(2)若点是轴上的一点,在抛物线上是否存在点,使以,,,为顶点且以为一边的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
2.如图,在平面直角坐标系中,已知抛物线与x轴交于,两点,与y轴交于点C,连接.
(1)求该抛物线的解析式;
(2)点P为直线上方的抛物线上一点,过点P作y轴的垂线交线段于M,过点P作x轴的垂线交线段于N,求的周长的最大值.
(3)若点N为抛物线对称轴上一点,抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请求出所有满足条件的点M的坐标;若不存在,请说明理由.
3.如图,已知抛物线与x轴交于A,B两点(A点在B点的左边),与y轴交于点C.
(1)如图1,若,则n的值为______(直接写出结果);
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以为边,以点B、C、P、Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线的平行线交抛物线于另一点D,交y轴于点E,若,求n.
4.抛物线经过、两点,且,直线过点,,点是线段(不含端点)上的动点,过作轴交抛物线于点,连接、.
(1)求抛物线与直线的解析式;
(2)求证:为定值;
(3)在第四象限内是否存在一点,使得以、、、为顶点的平行四边形面积最大,若存在,求出点坐标;若不存在,请说明理由.
5.如图1,抛物线与x轴交于A,B.两点(点A在点B的左边),与y轴交于点C,直线经过点A,C.
(1)求直线的解析式;
(2)点P为直线上方抛物线上的一个动点,过点P作于点D,过点P作交x轴于点E,求的最大值及此时点P的坐标;
(3)在(2)问取得最大值的情况下,将该抛物线沿射线方向平移个单位后得到新抛物线,点M为新抛物线对称轴上一点,在新抛物线上确定一点N,使得以点P,C,M,N为顶点的四边形是平行四边形,写出所有符合条件的点M的坐标,并写出求解点M的坐标的其中一种情况的过程.
6.在平面直角坐标系中,抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为.
(1)求点C的坐标;
(2)如图1,若点P是第二象限内抛物线上一动点,求点P到直线距离的最大值,并求出此时点P的坐标;
(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
7.如图1,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C,连接.
(1)求△ABC的面积;
(2)如图2,点P为直线上方抛物线上的动点,过点P作交直线于点D,过点P作直线轴交直线于点E,求的最大值及此时P的坐标;
(3)在(2)的条件下,将原抛物线向右平移2个单位,再向上平移8个单位,点M是新抛物线与原抛物线的交点,N是平面内任意一点,若以P、B、M、N为顶点的四边形是平行四边形,请直接写出点N的坐标.
8.如图,抛物线与轴交于和两点,与轴交于点,点是直线下方的抛物线上一动点.
(1)求抛物线的解析式;
(2)过点作轴于点D,交直线于点,求线段的最大值及此时点的坐标;
(3)取(2)中最大值时的P点,在坐标平面内是否存在点,使得以点、、、为顶点的四边形为平行四边形?若存在,直接写出点的坐标,若不存在,请说明理由.
9.如图,抛物线与x轴交于两点,且,与y轴交于点,其中是方程的两个根.
(1)求这条抛物线的解析式;
(2)点M是线段上的一个动点,过点M作,交于点N,连接,当的面积最大时,求点M的坐标;
(3)点在(1)中抛物线上,点E为抛物线上一动点,在x轴是否存在点F,使以A,D,E,F四点为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;如果不存在,请说明理由.
10.如图,在平面直角坐标系中,抛物线与直线交于点,.
(1)求该抛物线的函数表达式;
(2)点是直线下方抛物线上的一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,求的最大值及此时点的坐标;
(3)在(2)中取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点为点的对应点,平移后的抛物线与轴交于点,为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点,使得以点,,,为顶点的四边形是平行四边形,直接写出所有符合条件的点的坐标.
11.如图,已知抛物线与一直线相交于,两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线的解析式.
(2)设点,求使的值最小时m的值.
(3)若抛物线的对称轴与直线相交于点B,E为直线上的任意一点,过E作交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求出点E,F的坐标;若不能,请说明理由.
12.综合与探究
如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,抛物线)经过,两点,与轴相交于另一点,连接.点是线段上方抛物线上的一个动点,过点作交线段于点.
(1)求抛物线的解析式;
(2)点为抛物线对称轴上的一个动点,则的最大值是___________;
(3)求的最大值,并写出此时点的坐标;
(4)在轴上找一点,抛物线上找一点,使以点为顶点的四边形是平行四边形,请直接写出点的坐标.
13.如图1,在平面直角坐标系中,抛物线与轴交于点,点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)点P为直线上方抛物线上的一点,过点P作x轴的平行线交于点D,过点P作y轴的平行线交于点E,求的最大值以及此时点P的坐标;
(3)如图2,将抛物线沿射线的方向平移,使得平移后的抛物线经过线段的中点,且平移后抛物线的对称轴与x轴交于点M,N,R是直线BC上任意两点,Q为新抛物线上一点,直接写出所有使得以点M,N,R,Q为顶点的四边形是平行四边形的点Q的横坐标,并把求其中一个点的横坐标过程写出来.
14.抛物线()与x轴交于点,两点,与y轴交于点,点P是抛物线上的一个动点.
(1)求抛物线的函数表达式;
(2)如图1,点P在线段上方的抛物线上运动(不与A,C重合),过点P作,垂足为D,交于点E.作,垂足为F,若点P的横坐标为t,请用t的式子表示,并求的面积的最大值;
(3)如图2,点Q是抛物线的对称轴l上的一个动点,在抛物线上存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形,请直接写出所有符合条件的点P的坐标,并把求其中一个点P的坐标的过程写下来.
15.综合与探究
如图1,在平面直角坐标系中,二次函数的图象与x轴交于A,B两点,与直线l交于B,C两点,其中点A的坐标为,点C的坐标为.
(1)求二次函数的表达式和点B的坐标.
(2)若P为直线l上一点,Q为抛物线上一点,当四边形为平行四边形时,求点P的坐标.
(3)如图2,若抛物线与y轴交于点D,连接,抛物线上是否存在点M,使?若存在,请直接写出点M的坐标;若不存在,请说明理由.
16.在直角坐标系中,抛物线与x轴交于A、B两点.其中点,点.
(1)求抛物线的解析式.
(2)如图1,在直线经过点,与轴交于.在直线l下方的抛物线上有一个动点,连接,,求面积的最大值及其此时的坐标.
(3)将抛物线y向右平移个单位长度后得到新抛物线,点是新抛物线的对称轴上的一个动点,点是原抛物线上的一个动点,取面积最大值时的点.若以点、、、为顶点的四边形是平行四边形,直接写出点的坐标,并写出求解其中一个点的过程.
17.如图,已知抛物线的顶点为点,且与轴交于,两点(在的左侧),与轴交于点.点为抛物线对称轴上的一个动点:
(1)当点在轴上方且时,求的值;
(2)若点在抛物线上,是否存在以点,,,为顶点的四边形是平行四边形﹖请求出点的坐标;
(3)若抛物线对称轴上有点,使得取得最小值,连接并延长交第二象限抛物线为点,请直接写出的长度.
18.图1,在平面直角坐标系中,已知抛物线经过,两点.P是抛物线上一点,且在直线的上方.
(1)求抛物线的解析式;
(2)如图2,点E为中点,作轴交于点Q,若四边形为平行四边形,求点P的横坐标;
(3)如图3,连结,交于点M,作交于点H.记,,的面积分别为.判断是否存在最大值,若存在,求出最大值;若不存在,请说明理由.
19.如图,在平面直角坐标系中,抛物线与x轴交于两点(点A在点B的左侧),与y轴交于点C,连接,点P为直线上方抛物线上一动点,连接交于点Q.
(1)求抛物线的函数表达式;
(2)当的值最大时,求点P的坐标和的最大值;
(3)把抛物线向右平移1个单位,再向上平移2个单位得新抛物线,M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,写出所有符合条件的N点的坐标,并写出求解点N的坐标的其中一种情况的过程.
20.抛物线与x轴交于,与y轴交于点.
(1)求抛物线的表达式;
(2)如图1,M为抛物线对称轴l上一动点,连接,求的最小值及此时M点的坐标;
(3)如图2,抛物线的对称轴l与x轴交于点E,点,P为抛物线上一动点,Q为抛物线对称轴l上一动点,以点E、F、P、Q为顶点的四边形为平行四边形时,直接写出所有可能的点Q的坐标.
参考答案
1.(1)解:∵点的坐标为,
∴,
∵,
∴,
∴,
∵抛物线过点,
∴
解得
∴抛物线的函数关系式为;
(2)在抛物线上存在点,使以,,,为顶点且以为一边的四边形是平行四边形;
理由:①如图1,当点在轴下方时,则:,
∴点的纵坐标为,
令,则,
解得,,
∴点的坐标为;
②如图2,当点在轴上方时,
∵平行四边形的对角线分平行四边形为面积相等的两个三角形,点到轴的距离为3,
∴点到轴的距离为3,
令,则,
解得,
∴,,
综上可得,在抛物线上存在点,使以,,,为顶点且以为一边的四边形是平行四边形,点的坐标为或或.
2.(1)解:(1)抛物线过,两点,
,
解得,
抛物线的解析式为;
(2)当时,,即:,
则,,,
设的解析式为:,将,代入可得:
,解得:,
∴的解析式为:,
设,
∵点P为直线上方的抛物线上一点,过点P作y轴的垂线交线段于M,过点P作x轴的垂线交线段于N,
∴,则,
当时,点的纵坐标为:,
则 ,
∴当时,有最大值为:,
由题意可知,,轴,则,
∴,
则,则,,
的周长为,
则当最大时,的周长有最大值,
即:的周长的最大值为;
(3)存在点,使得以B,C,M,N为顶点的四边形是平行四边形,
①以为对角线,过C作轴交抛物线与M,点N在x轴上,,;
②以为边,过M作垂直抛物线对称轴于G,当,且时,四边形为平行四边形,M点横坐标,纵坐标,;
③过N作轴,与过M作轴交于H,当,时,四边形为平行四边形,M点横坐标为,纵坐标,;
综上所述:点的坐标为或或.
3.(1)解:∵抛物线与x轴交于A,B两点,
∴,,
∵,即,
∴
,
解得:;
(2)由(1)当时,
解得,,
,,
,,
抛物线对称轴为直线,
设点坐标为,,
由平行四边形性质可知,
当、为平行四边形对角线时,点坐标为,,
代入,
解得则点坐标为,,
当、为为平行四边形对角线时,点坐标为,,
代入,
解得则坐标为,,
综上点坐标为,,;
(3)设点坐标为,
,
则,,
,
,
,
,
,
由一元二次方程根与系数关系,
,
,
将点,,代入,
,
解得或(舍去),
则.
4.(1)解:令,则,
∴,
∵,
∴,
∴,
将点代入得:,
解得:,
∴抛物线的解析式为:;
设直线为,
将点,的坐标代入得,
,解得:,
∴直线的解析式是:;
(2)证明:设点,,如图,过点作轴于点,
则,则,,,
∴为定值;
(3)解:存在,理由:
①当是平行四边形的边时,
如下图:设直线交轴于点,交于点,
令,则,解得;
令,则,
∴,,则,
∴,,
过点作于点,则,
则,
则以、、、为顶点的平行四边形面积,
其中为常数,
故当最大时,平行四边形的面积最大,
设点,则点,
则,
即的最大值为,此时点;
②当是平行四边形的对角线时,如下图,
同理可得:以、、、为顶点的平行四边形面积,
此时,
∵当时,的值随最大而增大,而,
当时,最大值为,
故该种情况,不符合题设要求,
综上,点,即四边形为平行四边形时,符合题设要求,
设点,
由中点坐标公式得:,
解得:,
故点.
5.(1)解:当时,,
∴点,
当时,,
解得:,
∴点,
设直线的解析式为,
把点,代入得:
,解得:,
∴直线的解析式为;
(2)解:如图,过点P作轴于点F交于点G,
∵,,
∴,
∴,
设点,则点,
∴,,,
∵,
∴,
∵,
∴,
∴,即,
解得:,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,即,
解得:,
∴,
∴当时,有最大值,最大值为;此时点;
(3)解:∵,
∴原抛物线的顶点坐标为,
∵将该抛物线沿射线方向平移个单位后得到新抛物线,
∴相当于原抛物线沿x轴向右平移个单位,再沿y轴向上平移个单位后得到新抛物线,
∴新抛物线的解析式为,
∴新抛物线的对称轴为直线,
设点,,
若以对角线为对角线,有
,解得:,
此时点M的坐标为;
若以对角线为对角线,有
,解得:,
此时点M的坐标为;
若以对角线为对角线,有
,解得:,
此时点M的坐标为;
综上所述,点M的坐标为或或.
6.(1)解:将点代入得:,
解得:,
∴抛物线的表达式为:,
把代入得:,
∴点C的坐标为;
(2)解:过点P作轴于点D,交于点F,过点P作于点E,
∵,,
∴,
∴,
∵,轴,
∴,
∵,
∴,
∴,
在中,,
设直线的函数表达式为:,
将点,代入得:
,解得:,
∴直线的函数表达式为:,
设点,则,
∴,
∴当时,有最大值,最大值为,
∴.
把代入得:,
∴,
综上:点P到直线距离为,此时;
(3)解:由(1)可得,抛物线的表达式为:,
∴该抛物线是对称轴为直线,
∵点N再抛物线对称轴上,点M在抛物线上,
∴设点,,
①当为平行四边形的对角线时,
∵,,
∴中点为,
∵,,
∴,解得:,
∴,
∴;
②当为平行四边形的对角线时,
∵,,
∴中点为,
∵,,
∴,解得:,
∴,
∴
③当为平行四边形的对角线时,
∵,,
∴中点为,
∵,,
∴,解得:,
∴,
∴
综上:点M的坐标为或或.
7.(1)解:令,则,
解得或4,
∴,
∴,
令,则,
∴,
∴,
∴;
(2)解:∵,,
∴,
∵轴,
∴,
∵,
∴,
∴,
∴,即,
∴,
设直线的解析式为,
∴,解得,
∴直线的解析式为,
设,则,
∴,
∴,
∴当时,的值最大,最大值为,
此时;
(3)解:∵原抛物线向右平移2个单位,再向上平移8个单位得到新抛物线,
∴平移后的抛物线的解析式为,
联立方程组,解得,
∴,
设,
①当为平行四边形的对角线时,
,解得,
∴;
②当为平行四边形的对角线时,
,解得,
∴);
③当为平行四边形的对角线时,
,解得,
∴;
综上所述:N点坐标为或或.
8.(1)解:把,代入得:
解得,
抛物线的函数表达式为;
(2)由题意可得,则,
由题意可得直线过点、,则
设函数解析式为:,
依题意得:
解得:
的函数关系式为,
令,则,
∴当时,的最大值为4.
∴;
(3)存在.点的坐标为或或.
解:设,又、、,
当、为平行四边形的对角线时,与的中点重合,
∴,
解得:,
∴;
当、为平行四边形的对角线时,与的中点重合,
∴,
解得:,
∴;
当、为平行四边形的对角线时,与的中点重合,
∴,
解得:,
∴;
综上所述,点的坐标为或或.
9.(1)解:解方程得,则,
设抛物线解析式为,
把代入得,
解得,
∴抛物线解析式为;
(2)解:作轴于H,如图1,
设,
,
,
,即,
,
,
当时,的面积最大,此时M点的坐标为;
(3)解:当时,,则,
如图2,当,则,
∴,
∴此时F点坐标为或;
当 时,则点E和点D的纵坐标互为相反数,即点E的纵坐标为5,
当时,,
解得,
若E点坐标为,由于点向右平移5个单位,向下平移5个单位得到D点,则E点向右平移5个单位,向下平移5个单位得到F点,此时F点坐标为;
若E点坐标为,同样方法得到此时F点坐标为;
总上所述,满足条件的F点坐标为或或或.
10.(1)解:将点,代入得:,
解得:,
∴该抛物线的函数表达式为:;
(2)解:如图,设交于H,
∵,,
∴,
∴,
∵,,
∴,,
∴,
设直线的解析式为,
则,解得:,
∴直线的解析式为,
设,则,,
∴
,
∴当时,取得最大值,此时;
(3)解:由题意得:平移后抛物线解析式为,,
∴,
∵抛物线的对称轴为,
∴设,,
分情况讨论:
①当为对角线时,
则,
解得:,此时,
∴点N的坐标为;
②当为对角线时,
则,即,
此时,
∴点N的坐标为;
③当为对角线时,
则,即,
此时,
∴点N的坐标为,
综上所述,点N的坐标为或或.
11.(1)解;将,两点代入得,,
解得,
∴,
设直线的解析式为,
将,两点代入得,,
解得,
∴,
∴抛物线的解析式为,直线的解析式为;
(2)解:当,,
当,,
当,或,
∴,,抛物线与 轴的另一个交点坐标为,
∵,
如图,作直线平行于轴,则在直线上,作关于直线的对称点,连接,与直线交点为,连接,
由题意知,,,
∴,
∴当三点共线时,的值最小且为,
设直线的解析式为,
将点坐标代入得,
解得,
∴直线的解析式为,
将代入得,,
∴的值为;
(3)解:将代入得,,
∴,,
设,则,
∵以B,D,E,F为顶点的四边形为平行四边形,
∴,
∴,
①当,解得,(与重合,舍去),
∴,则,,
②当,解得,,
∴,则,,
,则,,
综上所述,以B,D,E,F为顶点的四边形能为平行四边形,,或,或,.
12.(1)解:∵直线与轴交于点,与轴交于点,
∴,,
∵抛物线)经过,两点,
∴,
解得,
∴抛物线的解析式为:,
(2)解:取关于对称轴的对称点,对称轴,
∴,
解方程得到,
∴,
∵,
∴当共线时,有最大值,
∴,
∴故答案为:;
(3)解:过点做轴交于点,
设直线的解析式为:,
∵,
∴,
∴直线的解析式为,
设,则,
∴,
∴当时,有最大值,
∴,
∵轴,
∴,
∵,
∴,
∴,
∴当最大时,最大,
∴此时;
(4)解:①为对角线,
∵,在轴上,
∴轴,为的对称点,
∴,,
∴,
∴,
②为边,为对角线,设,,
∴,
∴或(舍去),
∴,
∴,
③为边,为对角线,设,,
∴,
∴,
∴,
∴或,
综上可得到:、、、.
13.(1)解:将,点代入,
得,
解得,
该抛物线的解析式为;
(2)解: ,
,
轴,
.
又由题知是直角三角形,,
,
,
当最大时,的长最大,
设直线的解析式为:,
直线经过点,,
代入得:,
解得,
,
设,则,
,
,
当时,有最大值,,
,此时;
(3)解:由(2)得,,
∴中点的坐标为,
∴可以看作点C向右移动个单位长度,向下移动个单位长度,
∵抛物线经过点C,平移后的抛物线经过中点,
∵
∴平移后的抛物线的解析式为:,
对称轴为,
∴与x轴的交点坐标为,
设点Q的坐标为:
当为平行四边形的对角线时,如图所示:
对角线的交点仍在直线上,
∴的中点为,代入直线解析式得:
,
解得:,;
当为平行四边形的边时,,
设直线的解析式为,且,
将点代入得,
解得:,
∴直线的解析式为,
将点Q代入得: ,
解得:,
综上可得:点的横坐标为:或或或.
14.(1)解:将,,三点代入解析式得,
,
解得:,,,
∴;
(2)解:设解析式为,
将, 代入解析式可得,
,
解得:,
∴,
∵点P的横坐标为t,
∴,
∵,
∴,
∴,
∵, ,
∴,
∵,,
∴,
∴是等腰直角三角形,
过F作,
∵,
∴,
∴,
∴当时,面积最大,
;
(3)解:由(1)得,
,
设,
∵点A,P,C,Q为顶点的四边形是平行四边形,
①当为对角线时,
P点坐标为,
∴,
解得:,
;
②当为对角线时,
P点坐标为,
∴,
解得:,
;
③当为对角线时,
P点坐标为,
∴,
解得:,
;
综上所述:,,;
15.(1)解:∵点A的坐标为,点C的坐标为,
∴,解得:,
∴二次函数的表达式为;
令,则,
解得:,
∴点B的坐标为;
(2)解:如图,
∵点B的坐标为,
∴,
设直线l的解析式为,
把点,代入得:
,解得:,
∴直线l的解析式为,
∵四边形为平行四边形,
∴,
∴轴,
设点P的坐标为,则点Q的坐标为,
∴,
∴,
解得:或0(舍去),
∴点P的坐标为;
(3)解:对于,
令,,
∴点D的坐标为,
∴,
∵点,
∴,,
如图,过点A作于点E,
∵,
∴,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
过点M作轴于点F,
∴是等腰直角三角形,
∴,
设点M的坐标为,
∴,
∴,
解得:(舍去)或2或4,
∴点M的坐标为或.
16.解:(1)∵抛物线与x轴交于、两点.其中点,点
∴
(2)将代入,
得:
解得:
∴
令,解得:,
∴,
如图所示,过点作轴交于点,
设,则,
∴ ,
∴
,
∴对称轴为,且,
∴面积最大值为,
此时,;
(3)∵点,点关于对称,
则抛物线的对称轴为直线,
∵将抛物线y向右平移1个单位长度后得到新抛物线,
∴则平移后新抛物线的对称轴为直线,
设,,
①若以为对角线时,
,
解得:,
∴,
②为对角线时,
,
解得:,当时,,
∴,
③若以为对角线时,
,
解得:,当时,,
∴,
综上所述,或或.
17.(1)解:∵,
令,解得,,
即,,
把代入中,
得,
即,
∵,
∴对称轴是直线,
顶点,
设对称轴与x轴交于点F,
∴,,,
∵,
∴,
在,.
(2)解:存在
∵点在抛物线上,点在对称轴上,
∴可设,,,
①以为对角线时,由平行四边形的对角线互相平分;则,
∴,
解得,即;
同理②以为对角线时,,
解得,即;
③以为对角线时,,
解得,即;
综上所述,存在,,,使得点,,,为顶点的四边形是平行四边形;
(3)解:如图所示,过点作于点,交对称轴于点,连接并延长交第二象限抛物线为点,
在中,,
∴,
∴,
∴要取得最小值,即要最小,
∴当点,,三点共线且垂直时最小,
此时最小,
在,中,,
∴,
∴,即,
∵,
设直线的解析式为:,
则,
解得:,
∴的解析式为:,
联立,
解得或(舍去)
∴,
∴.
18.解:(1)∵抛物线经过,,
∴,
解得,
∴,
(2)当时,,
∴点C的坐标是,
∴,
∵四边形为平行四边形,E为中点,
∴,
设直线的解析式为,
则,
∴直线的解析式为,
设,
∴,
,
,
∴点P的横坐标为;
(3)∵,
∴,
,
作交y轴于N,作轴交于Q,
∴, ,
∴,
∴,,
∵,,
∴,
∴,
设,则,
∴,
.
∴最大值.
即存在最大值,最大值为.
19.(1)解:抛物线与x轴交于、两点(点A在点B的左侧),
,
解得:,
抛物线的函数表达式为;
(2)解:抛物线与y轴交于点C,
,
,
设直线的解析式为,把,代入,得:
,
解得:,
直线的解析式为,
如图1,过点P作轴交于点D,
设,则,
,
,
,
,
当时,取得最大值,此时,;
(3)解:∵向右平移1个单位,再向上平移2个单位得新抛物线,
新抛物线解析式为,对称轴为直线,
设,,
①当为的边时,
则,,
,
解得:,
;
②当为的边时,
则,,
,
解得:,
;
③当为的对角线时,
则,
解得:,
;
综上所述,N点的坐标为: 或或.
20.(1)解:将代入得,,
解得,,
∴抛物线的表达式为;
(2)解:如图1,连接,交于,连接,
由题意知,抛物线的对称轴为直线,,
∴当三点共线时,,此时值最小,
当时,,
∴,
在中,由勾股定理得,
∴值最小为;
设直线的解析式为,
将,代入得,,
解得,,
∴直线的解析式为,
当时,,
∴,
∴的最小值为,;
(3)解:设,以点E、F、P、Q为顶点的四边形为平行四边形时,分两种情况求解:
①为平行四边形的边;
如图2,四边形为平行四边形,
∴,,
∴,,
∴;
如图3,四边形为平行四边形,
∴的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
②为平行四边形的对角线;
如图4,四边形为平行四边形,
的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
综上所述,以点E、F、P、Q为顶点的四边形为平行四边形时,所有可能的点Q的坐标为,,.
同课章节目录
