江西省吉安市永丰中学北师大版数学必修一3.6《指数函数、幂函数、对数函数增长的比较》课件(共19张PPT)
文档属性
| 名称 | 江西省吉安市永丰中学北师大版数学必修一3.6《指数函数、幂函数、对数函数增长的比较》课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 300.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-05 00:00:00 | ||
图片预览



文档简介
课件19张PPT。永丰中学数学教研组§6 指数函数、幂函数、对数 函数增长的比较1.指数函数y=ax (a>1),对数函数y=logax(a>1)
和幂函数y=xn (n>0)在区间(0,+∞)上的单调性如何?
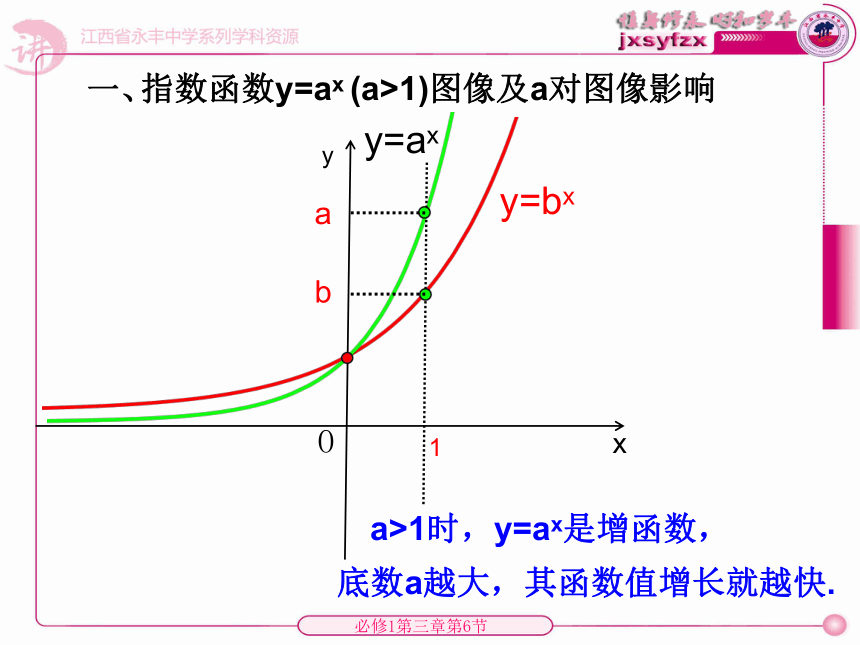
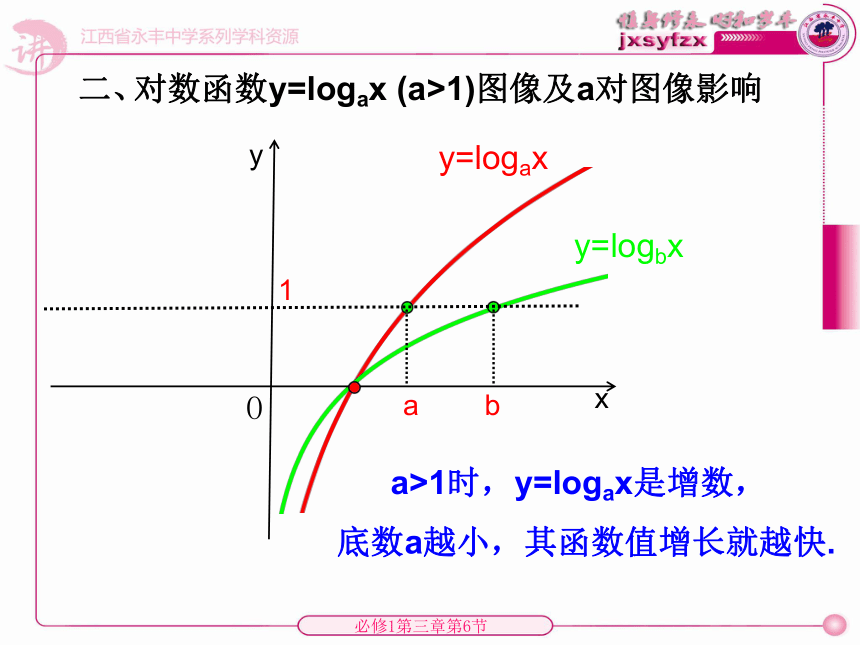
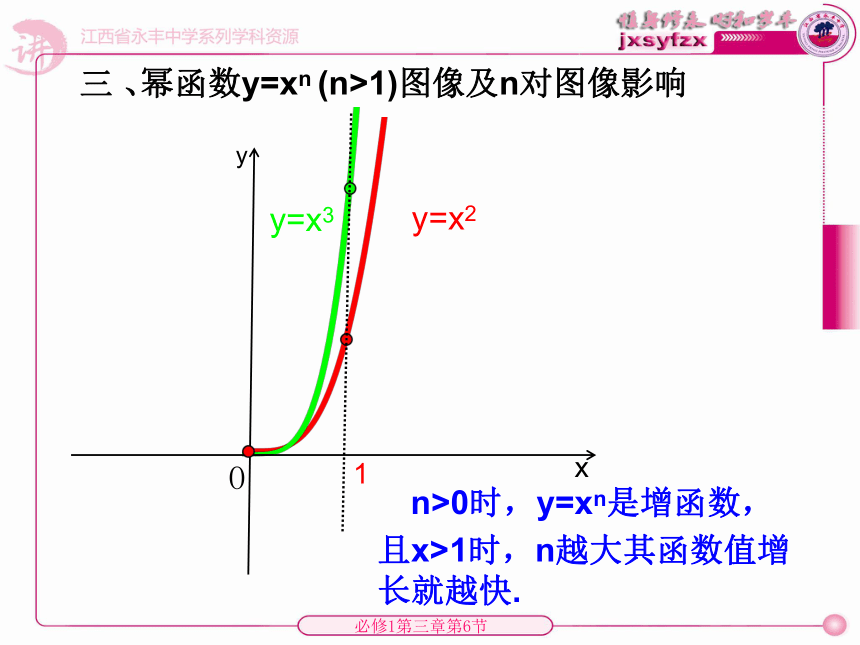
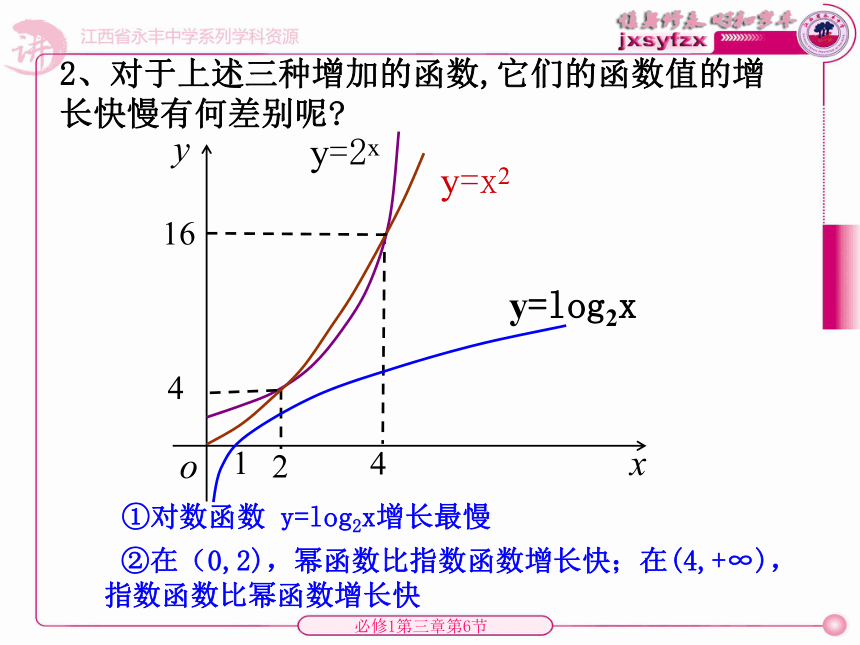
y=bxy=ax指数函数y=ax (a>1)图像及a对图像影响一、yxO1 a>1时,y=ax是增函数,底数a越大,其函数值增长就越快.y=logaxy=logbx对数函数y=logax (a>1)图像及a对图像影响二、 yxO a>1时,y=logax是增数,1ab底数a越小,其函数值增长就越快.y=x2y=x3幂函数y=xn (n>1)图像及n对图像影响三 、yxO n>0时,y=xn是增函数,且x>1时,n越大其函数值增长就越快.1124 ②在(0,2),幂函数比指数函数增长快;在(4,+∞),指数函数比幂函数增长快①对数函数 y=log2x增长最慢1642、对于上述三种增加的函数,它们的函数值的增长快慢有何差别呢?73、函数y=2x,y=x100(x>0),y=log2x 呢?借助计算器完成右表3.321 928 16.643 856 2 8.228 818 78.965 784 39.451 211 19.813 781 29.965 784 310.103287810.2288187利用上表完成右表1.584 962 50.736 965 60.485 426 80.362 570 10.152 003 10.137 503 50.125 530 9函数y=2x,y=x100(x>0),y=log2x的函数值增长比较:①、随着x的值越大,y=log2x的函数值增长的越来越慢,y=2x和y=x100的函数值增长的 越来越快y=log2x增长比y=2x和y=x100要慢的多。②、对函数y=2x和y=x100而言
在x比较小时,会存在y=x100比y=2x的增长快的情况。
当x比较大时,y=2x比y=x100增长得更快。 2、由于指数函数增长非常快,人们常称这种现象为“指数爆炸”。 ①对数函数增长最慢
②当自变量x大于某一个特定值时,指数函数比幂函数增长快1、指数函数、幂函数、对数函数增长的比较B1、函数 与 图像的交点个数为( )A.1B.2C.3D.42、0.32,log20.3,20.3这三个数之间大小关系是( )
A. 0.32<20.3<log20.3
B. 0.32<log20.3<20.3
C. log20.3<20.3<0.32
D. log20.3<0.32<20.3D3、作图像,试比较函数y=4x,y=x4,y=log4x的增长情况.416o①对数函数 y=log2x增长最慢 ②在(0,2),幂函数比指数函数增长快;
在(4,+∞),指数函数比幂函数增长快4、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前 一天多回报10元;
方案三:第一天回报0 .4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?令第x天,回报为y元
方案一: y=40
方案二: y=10x(x∈N+)
方案三: y=2x·0.4(x∈N+)分析投资5天以下选方案一
投资5-8天以下选方案二
投资8天以上选方案三② 运用指、幂、对函数模型的增长性,解决实际问题 ① 从特殊指、幂、对函数模型的增长性认识了“指数爆炸”这种现象课本第103页 1、2作业
和幂函数y=xn (n>0)在区间(0,+∞)上的单调性如何?
y=bxy=ax指数函数y=ax (a>1)图像及a对图像影响一、yxO1 a>1时,y=ax是增函数,底数a越大,其函数值增长就越快.y=logaxy=logbx对数函数y=logax (a>1)图像及a对图像影响二、 yxO a>1时,y=logax是增数,1ab底数a越小,其函数值增长就越快.y=x2y=x3幂函数y=xn (n>1)图像及n对图像影响三 、yxO n>0时,y=xn是增函数,且x>1时,n越大其函数值增长就越快.1124 ②在(0,2),幂函数比指数函数增长快;在(4,+∞),指数函数比幂函数增长快①对数函数 y=log2x增长最慢1642、对于上述三种增加的函数,它们的函数值的增长快慢有何差别呢?73、函数y=2x,y=x100(x>0),y=log2x 呢?借助计算器完成右表3.321 928 16.643 856 2 8.228 818 78.965 784 39.451 211 19.813 781 29.965 784 310.103287810.2288187利用上表完成右表1.584 962 50.736 965 60.485 426 80.362 570 10.152 003 10.137 503 50.125 530 9函数y=2x,y=x100(x>0),y=log2x的函数值增长比较:①、随着x的值越大,y=log2x的函数值增长的越来越慢,y=2x和y=x100的函数值增长的 越来越快y=log2x增长比y=2x和y=x100要慢的多。②、对函数y=2x和y=x100而言
在x比较小时,会存在y=x100比y=2x的增长快的情况。
当x比较大时,y=2x比y=x100增长得更快。 2、由于指数函数增长非常快,人们常称这种现象为“指数爆炸”。 ①对数函数增长最慢
②当自变量x大于某一个特定值时,指数函数比幂函数增长快1、指数函数、幂函数、对数函数增长的比较B1、函数 与 图像的交点个数为( )A.1B.2C.3D.42、0.32,log20.3,20.3这三个数之间大小关系是( )
A. 0.32<20.3<log20.3
B. 0.32<log20.3<20.3
C. log20.3<20.3<0.32
D. log20.3<0.32<20.3D3、作图像,试比较函数y=4x,y=x4,y=log4x的增长情况.416o①对数函数 y=log2x增长最慢 ②在(0,2),幂函数比指数函数增长快;
在(4,+∞),指数函数比幂函数增长快4、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前 一天多回报10元;
方案三:第一天回报0 .4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?令第x天,回报为y元
方案一: y=40
方案二: y=10x(x∈N+)
方案三: y=2x·0.4(x∈N+)分析投资5天以下选方案一
投资5-8天以下选方案二
投资8天以上选方案三② 运用指、幂、对函数模型的增长性,解决实际问题 ① 从特殊指、幂、对函数模型的增长性认识了“指数爆炸”这种现象课本第103页 1、2作业
