17.1勾股定理 同步练习题(含解析) 人教版八年级数学下册
文档属性
| 名称 | 17.1勾股定理 同步练习题(含解析) 人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 321.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 08:07:27 | ||
图片预览


文档简介
人教版八年级数学下册《17.1勾股定理》同步练习题
一、单选题
1.由线段a,b,c可以组成直角三角形的是( )
A. B.
C. D.
2.在中,,,的对边分别是a,b,c,若,则下列等式中成立的是( )
A. B. C. D.以上都不对
3.若一组勾股数的其中两个为5和12,则第三个勾股数是( )
A.13 B. C.13或 D.不确定
4.如图,在中,,则的长为( )
A. B. C. D.
5.已知,如图长方形中,,,将此长方形折叠,使点B与点D重合,折痕为,则的面积为( )
A.3 B.4 C.6 D.12
6.如图将一根长为的筷子,置于底面直径为,高为的圆柱形水杯中,设筷子露在杯子外面的长度为,则h的取值范围是( )
A. B. C. D.
7.如图,在中,平分交于点,分别是上的动点,则的最小值为( )
A. B. C. D.6
8.如图,教室墙面与地面垂直,点在墙面上,若米,米,点到的距离是米,一只蚂蚁要从点爬到点,它的最短行程是( )米
A. B. C. D.
二、填空题
9.在平面直角坐标系中,点到原点的距离是 .
10.如图,长方形的边长为2,长为1,点A在数轴上对应的数是0,以A点为圆心,对角线长为半径画弧,交数轴于点E,则这个点E表示的实数是 .
11.一艘轮船以的速度从港口出发向东北方向航行,同时另一艘轮船也从港口出发以的速度向东南方向航行,半小时后它们相距 .
12.已知某直角三角形的一条直角边和斜边长分别为和.
(1)该直角三角形的另一直角边长为________;
(2)该直角三角形斜边上的高为________.
13.在中,,,高,则 .
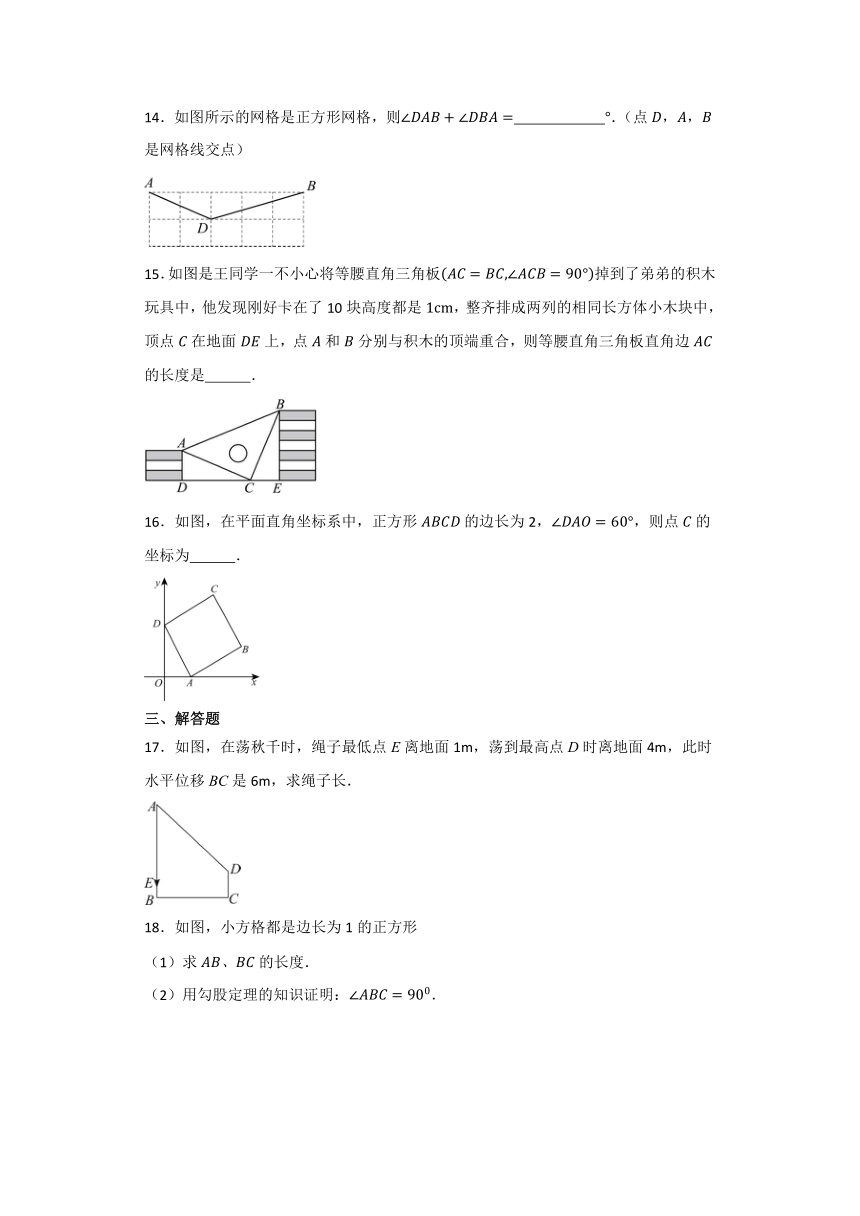
14.如图所示的网格是正方形网格,则 .(点是网格线交点)
15.如图是王同学一不小心将等腰直角三角板掉到了弟弟的积木玩具中,他发现刚好卡在了10块高度都是,整齐排成两列的相同长方体小木块中,顶点在地面上,点和分别与积木的顶端重合,则等腰直角三角板直角边的长度是 .
16.如图,在平面直角坐标系中,正方形的边长为2,,则点的坐标为 .
三、解答题
17.如图,在荡秋千时,绳子最低点E离地面1m,荡到最高点D时离地面4m,此时水平位移BC是6m,求绳子长.
18.如图,小方格都是边长为1的正方形
(1)求的长度.
(2)用勾股定理的知识证明:.
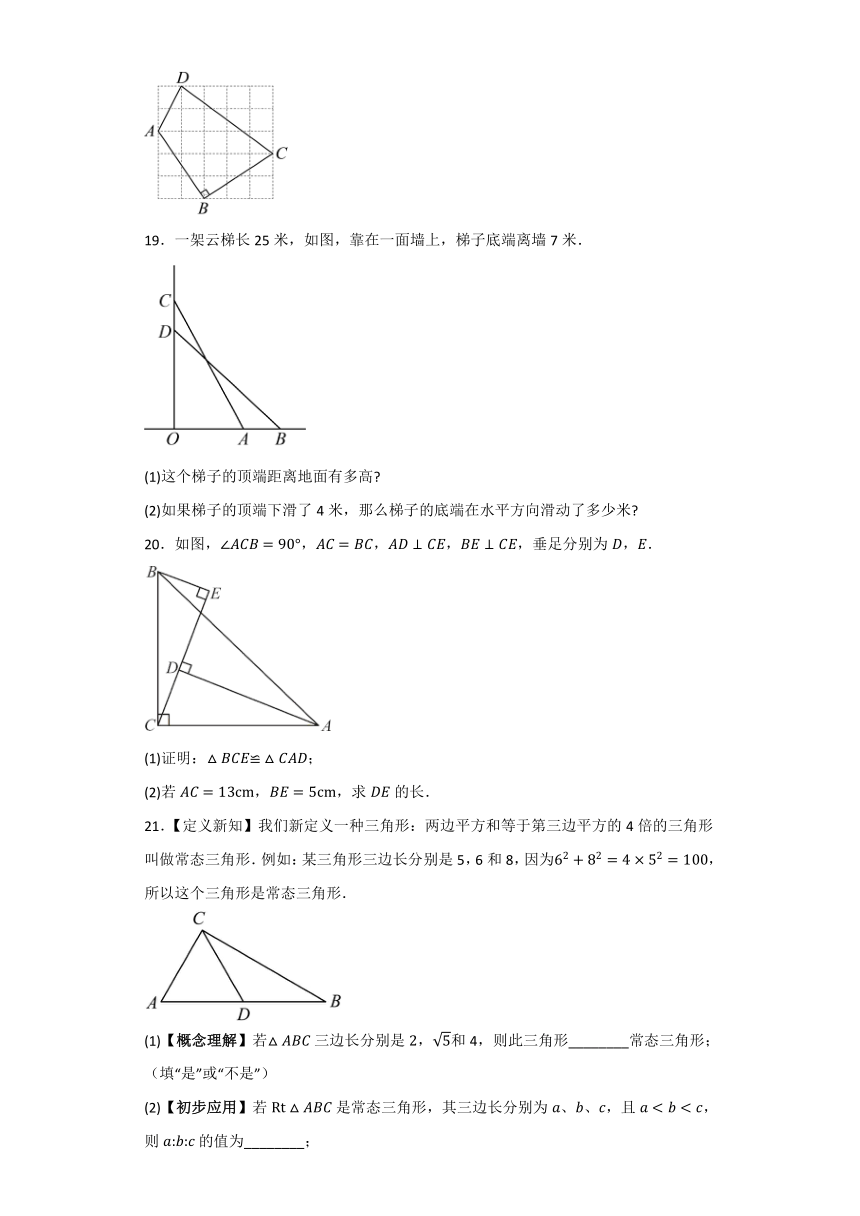
19.一架云梯长25米,如图,靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距离地面有多高
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了多少米
20.如图,,,,,垂足分别为,.
(1)证明:;
(2)若,,求的长.
21.【定义新知】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为,所以这个三角形是常态三角形.
(1)【概念理解】若三边长分别是,和4,则此三角形________常态三角形;(填“是”或“不是”)
(2)【初步应用】若是常态三角形,其三边长分别为、、,且,则的值为________;
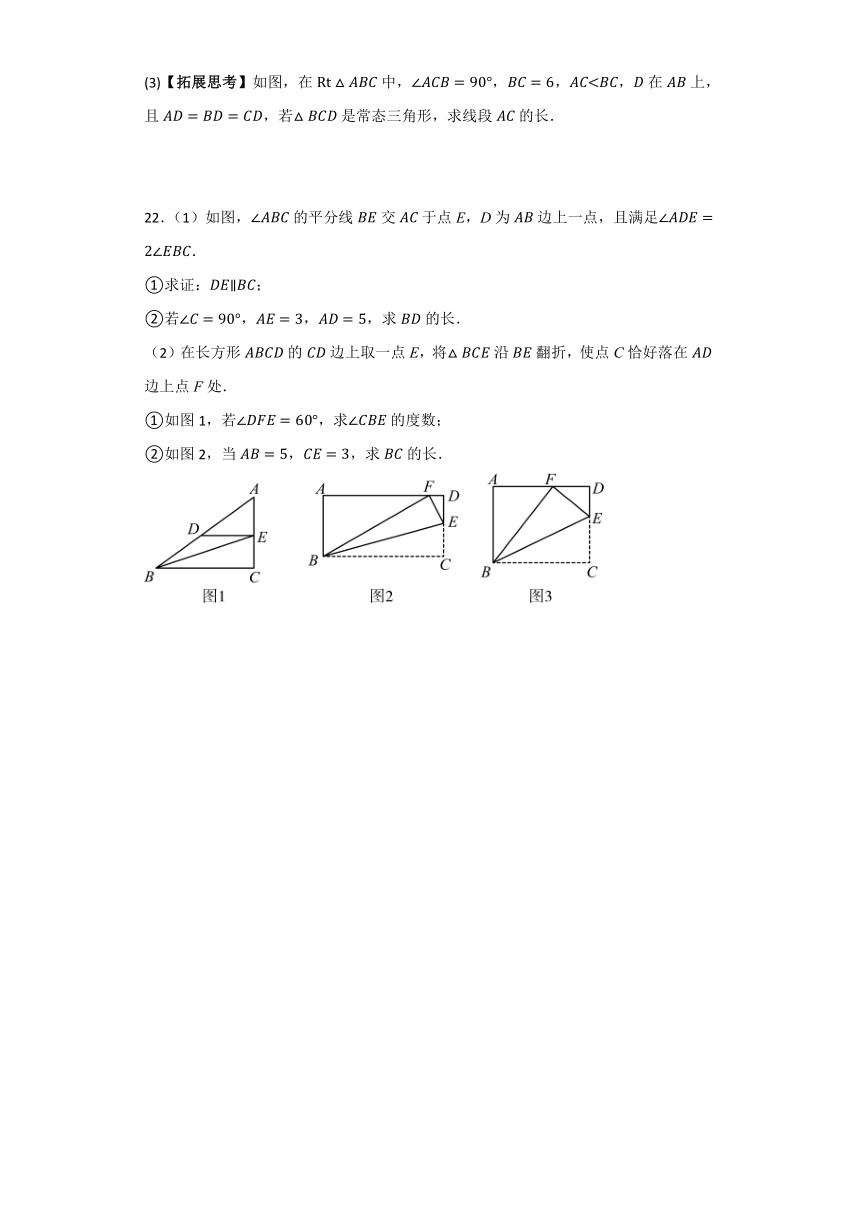
(3)【拓展思考】如图,在中,,,,在上,且,若是常态三角形,求线段的长.
22.(1)如图,的平分线交于点E,D为边上一点,且满足.
①求证:;
②若,,,求的长.
(2)在长方形的边上取一点E,将沿翻折,使点C恰好落在边上点F处.
①如图1,若,求的度数;
②如图2,当,,求的长.
参考答案
1.解:A、,故不是直角三角形,故选项不合题意;
B、,故不是直角三角形,故选项不合题意;
C、,故是直角三角形,故选项符合题意;
D、,故不是直角三角形,故选项不合题意.
故选:C.
2.解:∵在中,,
∴,
∴为直角三角形, 则根据勾股定理得:.
故选:C.
3.解:由题意知,5与12只能是两直角边,
第三个勾股数:,
故选:A.
4.解:∵,
∴,
故选:B.
5.解:∵长方形折叠,使点B与点D重合,
∴,
设,则,
在中,,
∴,
解得:,
∴的面积为.
故选:C.
6.解:当筷子与杯底垂直时h最大,h最大为:.
当筷子与杯底直径及杯高构成直角三角形时h最小,
此时杯内筷子长度:(),
此时h最小为:.
故h的取值范围是:.
故选:B.
7.解:如图所示:在上取点,使,过点C作,垂足为H.
在中,
.
,
,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为的长,
的值最小为,
故选:C.
8.解:如图,过作于,连接,
此时的长为这只蚂蚁从点爬到点的最短行程,
∵米,米,点到的距离是米,
∴米,
∴(米),
∴(米),
∴(米),
∴这只蚂蚁的最短行程应该是米.
故选:C.
9.解:点到原点的距离是,
故答案为:.
10.解:∵四边形是长方形,
∴,,,
在中,由勾股定理可得:
,
∵点A在数轴上对应的数是0,,
∴点E表示的实数是,
故答案为:.
11.解:如图,
因为东北和东南的夹角为,所以为直角三角形.
在中,(),
().
则().
故答案为: .
12.解:(1)由勾股定理可得另一直角边长为;
(2)设该直角三角形斜边上的高为,
根据面积相等可得,
解得:.
故答案为:(1);(2).
13.解:分两种情况讨论:①如图1,锐角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,,
由勾股定理得,
,
的长为;
②如图2,钝角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,
由勾股定理得,
,
的长为.
故答案为:12.5或5.5.
14.解:如图:延长交格点于,连接,
,,
,
是等腰直角三角形,
,
,
故答案为:.
15.解:由题意得:,,,,
,
,,
,
在和中,
,
,
,
,,
.
故答案为:.
16.解:∵正方形的边长为2,,,
∴,,
,,
如图,作轴于,
则,
四边形是正方形,
∴,
,
,
在和中,
,
,
,,
,
点在第一象限,
,
故答案为:.
17.解:设绳子长为米,过点作于,如下图:
由题意得:米,米,米,米
由勾股定理得:
解得:
答:绳子长为米
18.(1) 解:如图1,
在Rt△ABE中,AE=3,BE=2,
∴AB= = ,
在Rt△BCF中,BF=3,CF=2,
∴BC= = ;
(2)证明:如图2,连接AC,
在Rt△ACG中,AG=5,CG=1,
∴AC= ,
结合(1)可得 =
∴△ABC是以AC为斜边的直角三角形,
∴∠ABC=90°.
故答案为(1)AB= ,BC= ;(2)见解析.
19.(1)解:在中,,,
∴;
答:这个梯子的顶端距离地面有24米高;
(2)∵,
在中,,
∴,
∴.
答:梯子的底端在水平方向滑动了8米.
20.(1)证明: ,
,
,
,
,
,,
,
在与中,
;
(2)解: ,
,
,
∴,
∵,
∴,
根据勾股定理得:,
.
21.(1)解:∵,
∴此三角形是常态三角形,
故答案为:是;
(2)解:∵Rt△ABC是常态三角形,
∴设两直角边长为a,b,斜边长为c,
∴,
,
∴,
设,则,
∴此三角形的三边长之比为,
故答案为:;
(3)解:∵是常态三角形,
∴,
,
∴,
∴ (负值已舍),
∴,
,
在中,由勾股定理得,.
当时,
∵,
,,
在中,根据勾股定理得:,
∴的长为或.
22.解:(1)①∵平分,
∴,
又,
∴,
∴;
②∵平分,
∴,
∵,
∴,,
∴,
∴;
(2)∵,,
∴,
∵翻折,
∴,
又,
∴;
②∵翻折,
∴,,
∵,,
∴,
∴,
在中,,
∴,
∴,
解得.
一、单选题
1.由线段a,b,c可以组成直角三角形的是( )
A. B.
C. D.
2.在中,,,的对边分别是a,b,c,若,则下列等式中成立的是( )
A. B. C. D.以上都不对
3.若一组勾股数的其中两个为5和12,则第三个勾股数是( )
A.13 B. C.13或 D.不确定
4.如图,在中,,则的长为( )
A. B. C. D.
5.已知,如图长方形中,,,将此长方形折叠,使点B与点D重合,折痕为,则的面积为( )
A.3 B.4 C.6 D.12
6.如图将一根长为的筷子,置于底面直径为,高为的圆柱形水杯中,设筷子露在杯子外面的长度为,则h的取值范围是( )
A. B. C. D.
7.如图,在中,平分交于点,分别是上的动点,则的最小值为( )
A. B. C. D.6
8.如图,教室墙面与地面垂直,点在墙面上,若米,米,点到的距离是米,一只蚂蚁要从点爬到点,它的最短行程是( )米
A. B. C. D.
二、填空题
9.在平面直角坐标系中,点到原点的距离是 .
10.如图,长方形的边长为2,长为1,点A在数轴上对应的数是0,以A点为圆心,对角线长为半径画弧,交数轴于点E,则这个点E表示的实数是 .
11.一艘轮船以的速度从港口出发向东北方向航行,同时另一艘轮船也从港口出发以的速度向东南方向航行,半小时后它们相距 .
12.已知某直角三角形的一条直角边和斜边长分别为和.
(1)该直角三角形的另一直角边长为________;
(2)该直角三角形斜边上的高为________.
13.在中,,,高,则 .
14.如图所示的网格是正方形网格,则 .(点是网格线交点)
15.如图是王同学一不小心将等腰直角三角板掉到了弟弟的积木玩具中,他发现刚好卡在了10块高度都是,整齐排成两列的相同长方体小木块中,顶点在地面上,点和分别与积木的顶端重合,则等腰直角三角板直角边的长度是 .
16.如图,在平面直角坐标系中,正方形的边长为2,,则点的坐标为 .
三、解答题
17.如图,在荡秋千时,绳子最低点E离地面1m,荡到最高点D时离地面4m,此时水平位移BC是6m,求绳子长.
18.如图,小方格都是边长为1的正方形
(1)求的长度.
(2)用勾股定理的知识证明:.
19.一架云梯长25米,如图,靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距离地面有多高
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了多少米
20.如图,,,,,垂足分别为,.
(1)证明:;
(2)若,,求的长.
21.【定义新知】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为,所以这个三角形是常态三角形.
(1)【概念理解】若三边长分别是,和4,则此三角形________常态三角形;(填“是”或“不是”)
(2)【初步应用】若是常态三角形,其三边长分别为、、,且,则的值为________;
(3)【拓展思考】如图,在中,,,,在上,且,若是常态三角形,求线段的长.
22.(1)如图,的平分线交于点E,D为边上一点,且满足.
①求证:;
②若,,,求的长.
(2)在长方形的边上取一点E,将沿翻折,使点C恰好落在边上点F处.
①如图1,若,求的度数;
②如图2,当,,求的长.
参考答案
1.解:A、,故不是直角三角形,故选项不合题意;
B、,故不是直角三角形,故选项不合题意;
C、,故是直角三角形,故选项符合题意;
D、,故不是直角三角形,故选项不合题意.
故选:C.
2.解:∵在中,,
∴,
∴为直角三角形, 则根据勾股定理得:.
故选:C.
3.解:由题意知,5与12只能是两直角边,
第三个勾股数:,
故选:A.
4.解:∵,
∴,
故选:B.
5.解:∵长方形折叠,使点B与点D重合,
∴,
设,则,
在中,,
∴,
解得:,
∴的面积为.
故选:C.
6.解:当筷子与杯底垂直时h最大,h最大为:.
当筷子与杯底直径及杯高构成直角三角形时h最小,
此时杯内筷子长度:(),
此时h最小为:.
故h的取值范围是:.
故选:B.
7.解:如图所示:在上取点,使,过点C作,垂足为H.
在中,
.
,
,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为的长,
的值最小为,
故选:C.
8.解:如图,过作于,连接,
此时的长为这只蚂蚁从点爬到点的最短行程,
∵米,米,点到的距离是米,
∴米,
∴(米),
∴(米),
∴(米),
∴这只蚂蚁的最短行程应该是米.
故选:C.
9.解:点到原点的距离是,
故答案为:.
10.解:∵四边形是长方形,
∴,,,
在中,由勾股定理可得:
,
∵点A在数轴上对应的数是0,,
∴点E表示的实数是,
故答案为:.
11.解:如图,
因为东北和东南的夹角为,所以为直角三角形.
在中,(),
().
则().
故答案为: .
12.解:(1)由勾股定理可得另一直角边长为;
(2)设该直角三角形斜边上的高为,
根据面积相等可得,
解得:.
故答案为:(1);(2).
13.解:分两种情况讨论:①如图1,锐角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,,
由勾股定理得,
,
的长为;
②如图2,钝角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,
由勾股定理得,
,
的长为.
故答案为:12.5或5.5.
14.解:如图:延长交格点于,连接,
,,
,
是等腰直角三角形,
,
,
故答案为:.
15.解:由题意得:,,,,
,
,,
,
在和中,
,
,
,
,,
.
故答案为:.
16.解:∵正方形的边长为2,,,
∴,,
,,
如图,作轴于,
则,
四边形是正方形,
∴,
,
,
在和中,
,
,
,,
,
点在第一象限,
,
故答案为:.
17.解:设绳子长为米,过点作于,如下图:
由题意得:米,米,米,米
由勾股定理得:
解得:
答:绳子长为米
18.(1) 解:如图1,
在Rt△ABE中,AE=3,BE=2,
∴AB= = ,
在Rt△BCF中,BF=3,CF=2,
∴BC= = ;
(2)证明:如图2,连接AC,
在Rt△ACG中,AG=5,CG=1,
∴AC= ,
结合(1)可得 =
∴△ABC是以AC为斜边的直角三角形,
∴∠ABC=90°.
故答案为(1)AB= ,BC= ;(2)见解析.
19.(1)解:在中,,,
∴;
答:这个梯子的顶端距离地面有24米高;
(2)∵,
在中,,
∴,
∴.
答:梯子的底端在水平方向滑动了8米.
20.(1)证明: ,
,
,
,
,
,,
,
在与中,
;
(2)解: ,
,
,
∴,
∵,
∴,
根据勾股定理得:,
.
21.(1)解:∵,
∴此三角形是常态三角形,
故答案为:是;
(2)解:∵Rt△ABC是常态三角形,
∴设两直角边长为a,b,斜边长为c,
∴,
,
∴,
设,则,
∴此三角形的三边长之比为,
故答案为:;
(3)解:∵是常态三角形,
∴,
,
∴,
∴ (负值已舍),
∴,
,
在中,由勾股定理得,.
当时,
∵,
,,
在中,根据勾股定理得:,
∴的长为或.
22.解:(1)①∵平分,
∴,
又,
∴,
∴;
②∵平分,
∴,
∵,
∴,,
∴,
∴;
(2)∵,,
∴,
∵翻折,
∴,
又,
∴;
②∵翻折,
∴,,
∵,,
∴,
∴,
在中,,
∴,
∴,
解得.
