2024年中考数学高频考点突破——圆的切线证明(含解析)
文档属性
| 名称 | 2024年中考数学高频考点突破——圆的切线证明(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 00:00:00 | ||
图片预览


文档简介
2024年中考数学高频考点突破——
圆的切线证明
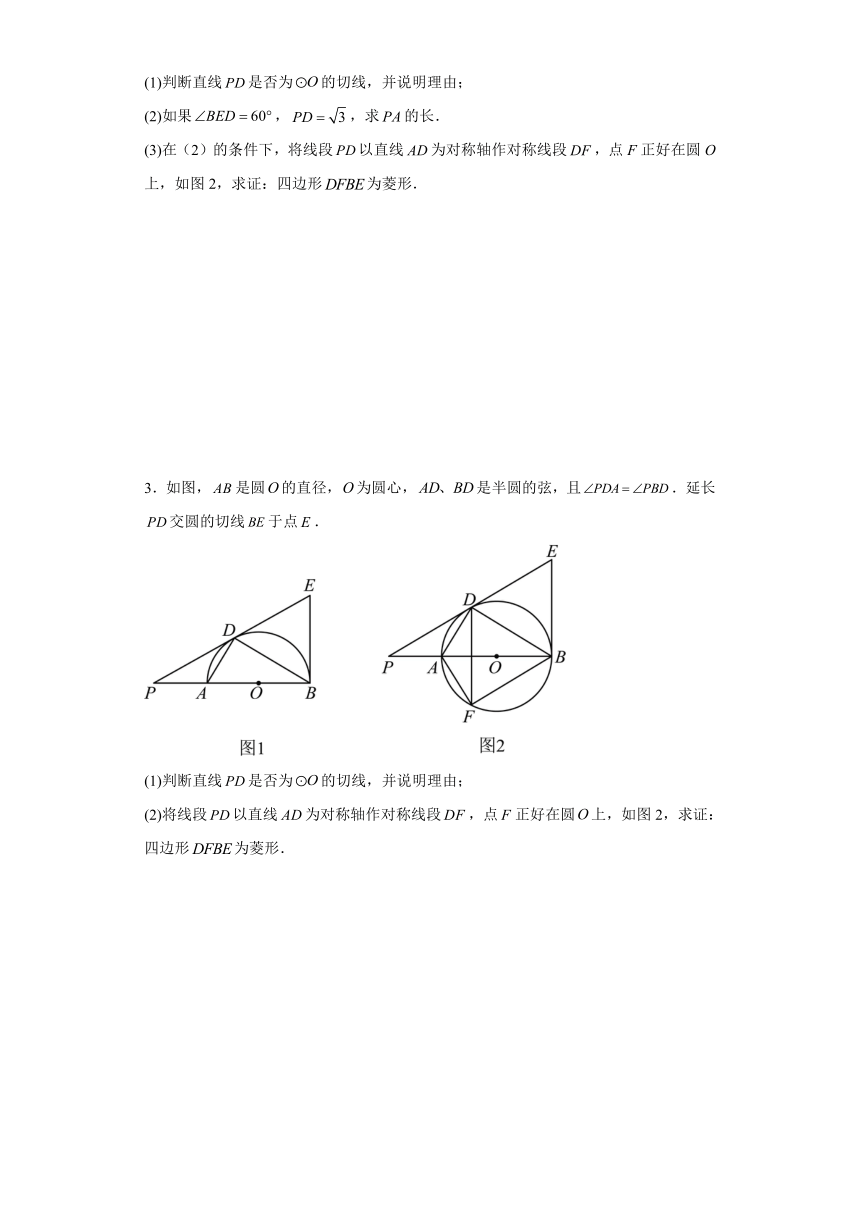
1.如图,是圆内接四边形的对角线,于点平分.
(1)求的度数;
(2)点在的延长线上,是该圆的切线.
①求证:是该圆的切线;
②若,直接写出的长.
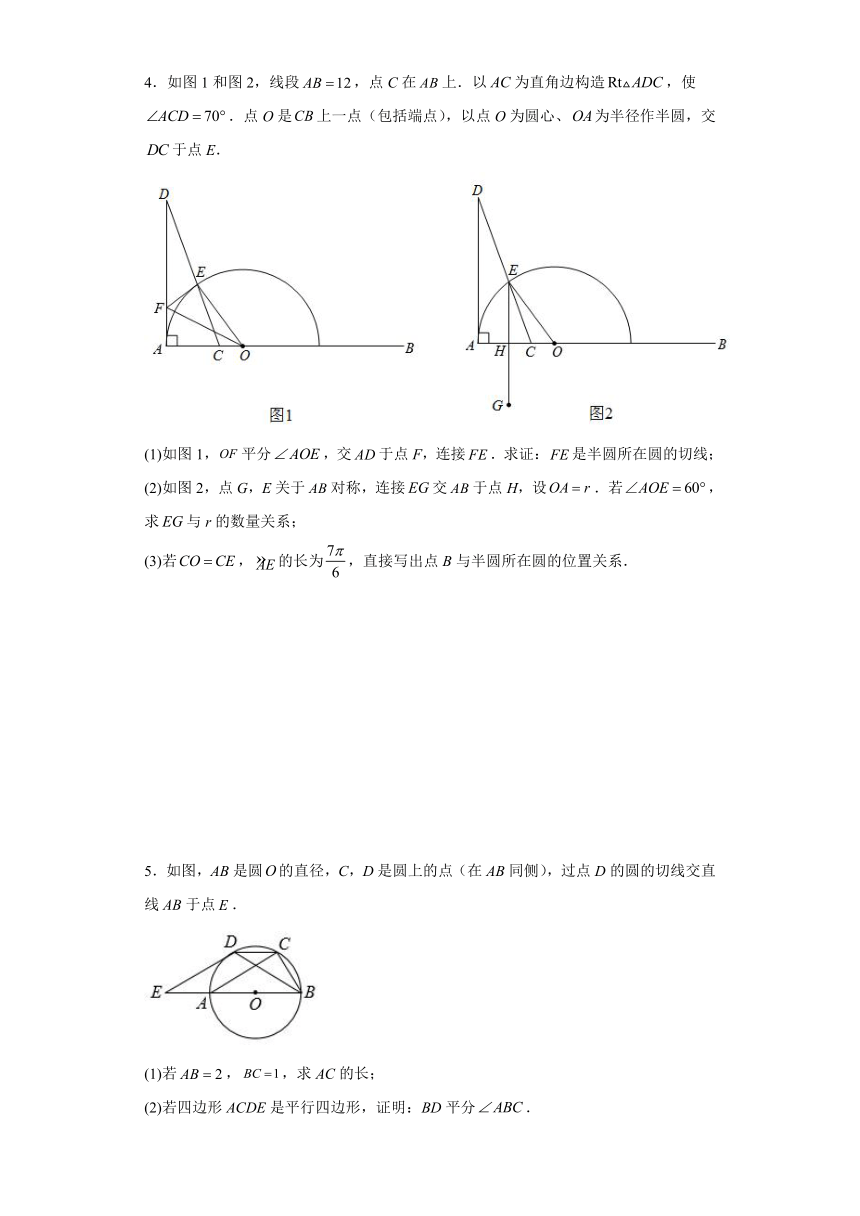
2.如图,是圆O的直径,O为圆心,、是半圆的弦,且.延长交圆的切线于点E.
(1)判断直线是否为的切线,并说明理由;
(2)如果,,求的长.
(3)在(2)的条件下,将线段以直线为对称轴作对称线段,点F正好在圆O上,如图2,求证:四边形为菱形.
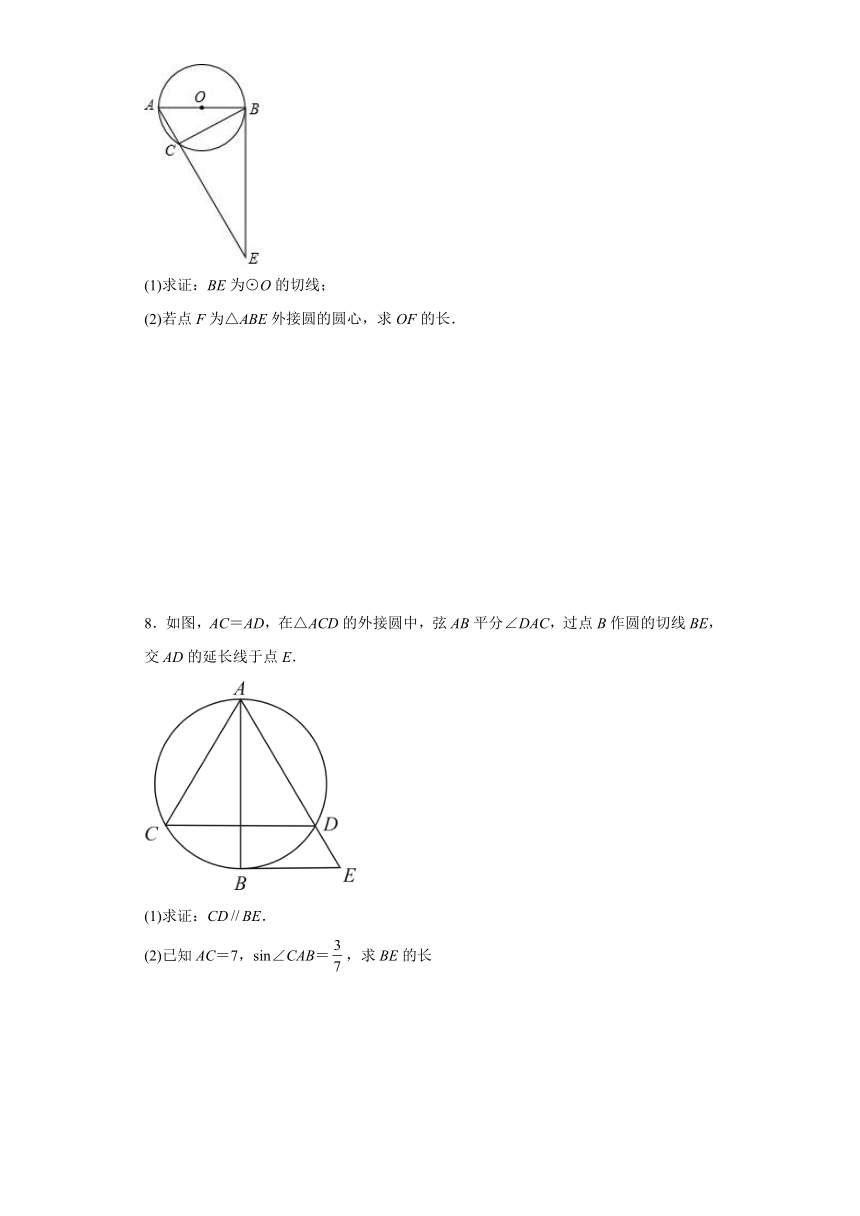
3.如图,是圆的直径,为圆心,是半圆的弦,且.延长交圆的切线于点.
(1)判断直线是否为的切线,并说明理由;
(2)将线段以直线为对称轴作对称线段,点正好在圆上,如图2,求证:四边形为菱形.
4.如图1和图2,线段,点C在上.以为直角边构造,使.点O是上一点(包括端点),以点O为圆心、为半径作半圆,交于点E.
(1)如图1,平分,交于点F,连接.求证:是半圆所在圆的切线;
(2)如图2,点G,E关于对称,连接交于点H,设.若,求与r的数量关系;
(3)若,的长为,直接写出点B与半圆所在圆的位置关系.
5.如图,AB是圆的直径,C,D是圆上的点(在AB同侧),过点D的圆的切线交直线AB于点.
(1)若,,求AC的长;
(2)若四边形ACDE是平行四边形,证明:BD平分.
6.如图,已知线段,点C为上一点,以点C为圆心,分别以,为半径在的上方作圆心角均为的扇形和扇形.
(1)求证:;
(2)已知,若是扇形所在圆的切线.
①求的长;
②判断和扇形所在圆的位置关系,并说明理由.
7.如图,已知点A、B、C在⊙O上,且AC=6,BC=8,AB=10.点E在AC延长线上,连接BE,且BE2=AE CE.
(1)求证:BE为⊙O的切线;
(2)若点F为△ABE外接圆的圆心,求OF的长.
8.如图,AC=AD,在△ACD的外接圆中,弦AB平分∠DAC,过点B作圆的切线BE,交AD的延长线于点E.
(1)求证:CDBE.
(2)已知AC=7,sin∠CAB=,求BE的长
9.如图,圆O是△ABP的外接圆,∠B=∠APC;
(1)求证:PC是圆的切线;
(2)若AP=6,∠B=45°,求劣弧AP的长.
10.如图1,四边形内接于,为延长线上一点,平分.
(1)求证:;
(2)如图2,若为直径,过点的圆的切线交延长线于,若,,求的半径.
11.如图,已知以的边为直径作的外接圆的平分线交于,交于,过作交的延长线于.
(1)求证:是切线;
(2)若求的长.
12.如图,在△ABC中,∠ABC=45°,它的外接圆的圆心O在其内部,连结OC,过点A作AD∥OC,交BC的延长线于点D.
(1)求证:AD是⊙O的切线;
(2)若∠BAD=105°,⊙O的半径为2,求劣弧AB的长.
13.如图,△ABC是钝角三角形,,圆O是△ABC的外接圆,直径PQ恰好经过AB的中点M,PQ与BC的交点为D,,l为过点C圆的切线,作,CF也为圆的直径.
(1)证明:;
(2)已知圆O的半径为3,求的值.
14.如图,AB是⊙O的直径,AD,BD是弦,点P在BA的延长线上,且,延长PD交圆的切线BE于点E.
(1)求证:PD是⊙O的切线;
(2)若,,求PA的长.
15.如图,线段BC所在的直线 是以AB为直径的圆的切线,点D为圆上一点,满足BD=BC,且点C、D位于直径AB的两侧,连接CD交圆于点E. 点F是BD上一点,连接EF,分别交AB、BD于点G、H,且EF=BD.
(1)求证:EF∥BC;
(2)若EH=4,HF=2,求的长.
试卷第1页,共3页
参考答案:
1.(1)
(2)②的长为3.
【详解】(1)解:平分,
.
,
.
,
.
.
;
(2)①证明:如图,取的中点,连接.
,
是该圆的直径.
点是该圆的圆心.
是的切线,
.
,
.
,
.
.
是的切线;
②∵、都是的切线,
∴,
∵,
∴,
∴是等边三角形,
∴,,
∴,是等边三角形,
∵,
∴,
∴,,
∴,
∴的长为3.
2.(1)是的切线,(2)1;
【详解】(1)直线为的切线,理由如下:
如图1,连接,
∵是的直径,
,
,
∵,
,
,
∴,即,
∵是的半径,
直线为的切线;
(2)为切线,
,
,
,
在中,,,
∴,
,
∵,
∴;
(3)如图2,连接,
由题意得:,,
,
∵,,
∴,
∴,
∴,,
,
为切线,
,
,
四边形为平行四边形,
∵、为切线,
∴,
四边形为菱形.
3.【详解】(1)解:直线为的切线,理由如下:
连接,如图所示:
∵是圆的直径,
,
,
又,
,
,
,
,
即,
点在上,
直线为的切线.
(2)证明:依题意得:,,
,
,
是圆的直径,
,
设,则,
四边形内接于,
,
即,解得,
,
是的切线,
,
,
是等边三角形,
,
又,
是等边三角形,
,
,
∴四边形为菱形.
4.(2)
(3)点B在半圆所在圆上
【详解】(1)证明:平分,
.
又,,
.
.
是半圆所在圆的切线.
(2)解:点G,E关于对称,
,.
又,,
.
.
(3)解:点B在半圆所在圆上.理由如下:
∵∠ACD=70,
∴∠ECO=110,
∵CO=CE,
∴∠COE=∠CEO=,
∴,
∴r=6,
∴AB=12=2r,
∴点B在半圆所在的圆上.
5.(1)
【详解】(1)∵AB是圆的直径,
∴
∴,∴(舍负值).
(2)连结BD,连结OD与AC交于点.
∵与圆相切于点,
∴,
∵四边形ACDE是平行四边形,
∴, ,
∴,,
∴,
∵,,
∴四边形OBCD是菱形,
∴平分.
6.(2)①;②相切
【详解】(1)(1)证明:由题意可知,,
∴,即.
在和中, ,
∴.
(2)(2)解:①由题意,得.
∵是扇形所在圆的切线,
∴.
在Rt△ACD中,,
∴,
∴,
∵,
∴,
∴,
∴.
②和扇形所在圆相切.
理由如下:
在和中, ,
∴,
∴.
由(1)得,
∴,即.
又∵点E在扇形所在的圆上,
∴和扇形所在圆相切.
7.(2)
【详解】(1)证明:∵AC=6,BC=8,AB=10.
∴AC2+BC2=AB2,
∴△ABC为直角三角形且∠ACB=90°,
∴∠ECB=90°,
∴AB为⊙O的直径,
∵BE2=AE CE,
∴,
又∵∠E=∠E,
∴△ECB∽△EBA,
∴∠ECB=∠EBA=90°,
∴EB⊥AB,
又∵OB为⊙O的半径,
∴BE为⊙O的切线;
(2)解:如图,连接BF,
在Rt△ABE中,tan∠BAE=,
在Rt△ABC中,tan∠BAE=,
∴,
解得BE=,
∵点F为△ABE外接圆的圆心,
∴AF=BF=EF,
∴点F为直角三角形ABE斜边AE的中点,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF=BE=×=.
8.(2)
【详解】(1)证明:设AB与CD的交点为F,连接BD,
∵AC=AD,AB平分∠DAC,
∴AB⊥CD,DF=CF,
∴AB是直径,
∵BE是△ACD的外接圆的切线,
∴BE⊥AB,
∴CDBE;
(2)解:∵AC=7,sin∠CAB=,
∴CF=3=DF,
∴AF=,
∵cos∠DAB=,
∴AB=,
∵tan∠DAB=,
∴,
∴BE=.
9.(2)劣弧AP的长为.
【详解】(1)证明:过点P作直径PQ,连接AQ,
∵PQ为⊙O的直径,
∴∠PAQ=90°,
∵=,
∴∠B=∠Q,
∵∠B=∠APC,
∴∠APC=∠Q,
∵∠Q+∠APQ=90°,
∴∠APQ +∠APC=90°,
∴∠CPQ=90°.
∴PC是圆O的切线;
(2)连接OP、OA,
∵=,
∴∠O=2∠B=90°,
∵OP=OA,
∴△AOP是等腰直角三角形,
∴,
∵AP=6,
∴OP=OA=,
∴劣弧AP的长=.
10.【详解】(1)证明:∵四边形ADBC内接于⊙O,
∴∠EDA=∠ACB,
由圆周角定理得,∠CDA=∠ABC,
∵AD平分∠EDC,
∴∠EDA=∠CDA,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:连接AO并延长交BC于H,AM⊥CD于M,
∵AB=AC,四边形ADBC内接于⊙O,
∴AH⊥BC,又AH⊥AE,
∴AE∥BC,
∵CD为⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC=90°,
∴四边形AEBH为矩形,
∴BH=AE=2,
∴BC=4,
∵AD平分∠EDC,∠E=90°,AM⊥CD,
∴DE=DM=1,AE=AM=2,
在Rt△ABE和Rt△ACM中,
∴Rt△ABE≌Rt△ACM(HL),
∴BE=CM,
设BE=x,CD=x+2,
在Rt△BDC中,x2+42=(x+2)2,
解得,x=3,
∴CD=5,
∴⊙O的半径为2.5.
11.(2)
【详解】(1)连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠OBE,
∵EF∥AC,
∴∠CAE=∠FEA,
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB,
∵AB是的直径,
∴∠AEB=90°,
∴∠FEO=90°,
∴EF是切线;
(2)∵∠FEA=∠OEB=∠OBE,∠F=∠F,
∴ FEA~ FBE,
∴,
即:,
∴AF×(AF+15)=10×10,解得:AF=5或AF=-20(舍去),
∴,
∵在Rt ABE中,AE2+BE2=AB2,
∴AE2+(2AE)2=152,
∴AE=.
12.(2)π.
【详解】解:(1)连接AO.
∵∠ABC=45°,∴∠AOC=2∠B=90°.
∵OC∥AD,∴∠OAD=90°,
∴AD是⊙O的切线;
(2)连接OB.
∵∠BAD=105°,∠OAD=90°,
∴∠OAB=15°.
∵OB=OA,∴∠ABO=15°,
∴∠AOB=150°,
∴劣弧AB的长=.
13.(2)
【详解】(1)∵CF为直径,l为切线,
∴,
又∵,
∴CF//DE,
∴∠BCF=∠CDE.
又∠CED=∠CBF=90°,
∴;
(2)连接AF,
由题意得:∠CDP=∠BDM=45°,
∵M为弦AB的中点,
∴OM垂直平分线段AB,
∴∠ADM=∠BDM=45°,
∴△ADB为等腰直角三角形,
∴∠ADB=∠ADC=90°,
∴,
∵∠AFC=∠ABC=45°,
∴AC=CF×sin45°=,
∴.
14.【详解】(1)证明:连接OD
∵AB是⊙O的直径
∴
∴
∵
∴
∵
∴
∴
即PD⊥OD
∴直线PD为⊙O的切线;
(2)解:∵BE是⊙O的切线
∴
∵
∴
∵PD为⊙O的切线
∴
设⊙O的半径为
在Rt△PDO中,,则
∵
∴
解得
∴,
∴;
15.(2)
【详解】(1)∵EF=BD,
∴=
∴
∴∠D=∠DEF
又BD=BC,
∴∠D=∠C,
∴∠DEF=∠C
EF∥BC
(2)∵AB是直径,BC为切线,
∴AB⊥BC
又EF∥BC,
∴AB⊥EF,弧BF=弧BE,
GF=GE=(HF+EH)=3,HG=1
DB平分∠EDF,
又BF∥CD,
∴∠FBD=∠FDB=∠BDE=∠BFH
∴HB=HF=2
∴cos∠BHG==,∠BHG=60°.
∴∠FDB=∠BDE=30°
∴∠DFH=90°,DE为直径,DE=4,且弧BE所对圆心角=60°.
∴弧BE=×4=
答案第1页,共2页
圆的切线证明
1.如图,是圆内接四边形的对角线,于点平分.
(1)求的度数;
(2)点在的延长线上,是该圆的切线.
①求证:是该圆的切线;
②若,直接写出的长.
2.如图,是圆O的直径,O为圆心,、是半圆的弦,且.延长交圆的切线于点E.
(1)判断直线是否为的切线,并说明理由;
(2)如果,,求的长.
(3)在(2)的条件下,将线段以直线为对称轴作对称线段,点F正好在圆O上,如图2,求证:四边形为菱形.
3.如图,是圆的直径,为圆心,是半圆的弦,且.延长交圆的切线于点.
(1)判断直线是否为的切线,并说明理由;
(2)将线段以直线为对称轴作对称线段,点正好在圆上,如图2,求证:四边形为菱形.
4.如图1和图2,线段,点C在上.以为直角边构造,使.点O是上一点(包括端点),以点O为圆心、为半径作半圆,交于点E.
(1)如图1,平分,交于点F,连接.求证:是半圆所在圆的切线;
(2)如图2,点G,E关于对称,连接交于点H,设.若,求与r的数量关系;
(3)若,的长为,直接写出点B与半圆所在圆的位置关系.
5.如图,AB是圆的直径,C,D是圆上的点(在AB同侧),过点D的圆的切线交直线AB于点.
(1)若,,求AC的长;
(2)若四边形ACDE是平行四边形,证明:BD平分.
6.如图,已知线段,点C为上一点,以点C为圆心,分别以,为半径在的上方作圆心角均为的扇形和扇形.
(1)求证:;
(2)已知,若是扇形所在圆的切线.
①求的长;
②判断和扇形所在圆的位置关系,并说明理由.
7.如图,已知点A、B、C在⊙O上,且AC=6,BC=8,AB=10.点E在AC延长线上,连接BE,且BE2=AE CE.
(1)求证:BE为⊙O的切线;
(2)若点F为△ABE外接圆的圆心,求OF的长.
8.如图,AC=AD,在△ACD的外接圆中,弦AB平分∠DAC,过点B作圆的切线BE,交AD的延长线于点E.
(1)求证:CDBE.
(2)已知AC=7,sin∠CAB=,求BE的长
9.如图,圆O是△ABP的外接圆,∠B=∠APC;
(1)求证:PC是圆的切线;
(2)若AP=6,∠B=45°,求劣弧AP的长.
10.如图1,四边形内接于,为延长线上一点,平分.
(1)求证:;
(2)如图2,若为直径,过点的圆的切线交延长线于,若,,求的半径.
11.如图,已知以的边为直径作的外接圆的平分线交于,交于,过作交的延长线于.
(1)求证:是切线;
(2)若求的长.
12.如图,在△ABC中,∠ABC=45°,它的外接圆的圆心O在其内部,连结OC,过点A作AD∥OC,交BC的延长线于点D.
(1)求证:AD是⊙O的切线;
(2)若∠BAD=105°,⊙O的半径为2,求劣弧AB的长.
13.如图,△ABC是钝角三角形,,圆O是△ABC的外接圆,直径PQ恰好经过AB的中点M,PQ与BC的交点为D,,l为过点C圆的切线,作,CF也为圆的直径.
(1)证明:;
(2)已知圆O的半径为3,求的值.
14.如图,AB是⊙O的直径,AD,BD是弦,点P在BA的延长线上,且,延长PD交圆的切线BE于点E.
(1)求证:PD是⊙O的切线;
(2)若,,求PA的长.
15.如图,线段BC所在的直线 是以AB为直径的圆的切线,点D为圆上一点,满足BD=BC,且点C、D位于直径AB的两侧,连接CD交圆于点E. 点F是BD上一点,连接EF,分别交AB、BD于点G、H,且EF=BD.
(1)求证:EF∥BC;
(2)若EH=4,HF=2,求的长.
试卷第1页,共3页
参考答案:
1.(1)
(2)②的长为3.
【详解】(1)解:平分,
.
,
.
,
.
.
;
(2)①证明:如图,取的中点,连接.
,
是该圆的直径.
点是该圆的圆心.
是的切线,
.
,
.
,
.
.
是的切线;
②∵、都是的切线,
∴,
∵,
∴,
∴是等边三角形,
∴,,
∴,是等边三角形,
∵,
∴,
∴,,
∴,
∴的长为3.
2.(1)是的切线,(2)1;
【详解】(1)直线为的切线,理由如下:
如图1,连接,
∵是的直径,
,
,
∵,
,
,
∴,即,
∵是的半径,
直线为的切线;
(2)为切线,
,
,
,
在中,,,
∴,
,
∵,
∴;
(3)如图2,连接,
由题意得:,,
,
∵,,
∴,
∴,
∴,,
,
为切线,
,
,
四边形为平行四边形,
∵、为切线,
∴,
四边形为菱形.
3.【详解】(1)解:直线为的切线,理由如下:
连接,如图所示:
∵是圆的直径,
,
,
又,
,
,
,
,
即,
点在上,
直线为的切线.
(2)证明:依题意得:,,
,
,
是圆的直径,
,
设,则,
四边形内接于,
,
即,解得,
,
是的切线,
,
,
是等边三角形,
,
又,
是等边三角形,
,
,
∴四边形为菱形.
4.(2)
(3)点B在半圆所在圆上
【详解】(1)证明:平分,
.
又,,
.
.
是半圆所在圆的切线.
(2)解:点G,E关于对称,
,.
又,,
.
.
(3)解:点B在半圆所在圆上.理由如下:
∵∠ACD=70,
∴∠ECO=110,
∵CO=CE,
∴∠COE=∠CEO=,
∴,
∴r=6,
∴AB=12=2r,
∴点B在半圆所在的圆上.
5.(1)
【详解】(1)∵AB是圆的直径,
∴
∴,∴(舍负值).
(2)连结BD,连结OD与AC交于点.
∵与圆相切于点,
∴,
∵四边形ACDE是平行四边形,
∴, ,
∴,,
∴,
∵,,
∴四边形OBCD是菱形,
∴平分.
6.(2)①;②相切
【详解】(1)(1)证明:由题意可知,,
∴,即.
在和中, ,
∴.
(2)(2)解:①由题意,得.
∵是扇形所在圆的切线,
∴.
在Rt△ACD中,,
∴,
∴,
∵,
∴,
∴,
∴.
②和扇形所在圆相切.
理由如下:
在和中, ,
∴,
∴.
由(1)得,
∴,即.
又∵点E在扇形所在的圆上,
∴和扇形所在圆相切.
7.(2)
【详解】(1)证明:∵AC=6,BC=8,AB=10.
∴AC2+BC2=AB2,
∴△ABC为直角三角形且∠ACB=90°,
∴∠ECB=90°,
∴AB为⊙O的直径,
∵BE2=AE CE,
∴,
又∵∠E=∠E,
∴△ECB∽△EBA,
∴∠ECB=∠EBA=90°,
∴EB⊥AB,
又∵OB为⊙O的半径,
∴BE为⊙O的切线;
(2)解:如图,连接BF,
在Rt△ABE中,tan∠BAE=,
在Rt△ABC中,tan∠BAE=,
∴,
解得BE=,
∵点F为△ABE外接圆的圆心,
∴AF=BF=EF,
∴点F为直角三角形ABE斜边AE的中点,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF=BE=×=.
8.(2)
【详解】(1)证明:设AB与CD的交点为F,连接BD,
∵AC=AD,AB平分∠DAC,
∴AB⊥CD,DF=CF,
∴AB是直径,
∵BE是△ACD的外接圆的切线,
∴BE⊥AB,
∴CDBE;
(2)解:∵AC=7,sin∠CAB=,
∴CF=3=DF,
∴AF=,
∵cos∠DAB=,
∴AB=,
∵tan∠DAB=,
∴,
∴BE=.
9.(2)劣弧AP的长为.
【详解】(1)证明:过点P作直径PQ,连接AQ,
∵PQ为⊙O的直径,
∴∠PAQ=90°,
∵=,
∴∠B=∠Q,
∵∠B=∠APC,
∴∠APC=∠Q,
∵∠Q+∠APQ=90°,
∴∠APQ +∠APC=90°,
∴∠CPQ=90°.
∴PC是圆O的切线;
(2)连接OP、OA,
∵=,
∴∠O=2∠B=90°,
∵OP=OA,
∴△AOP是等腰直角三角形,
∴,
∵AP=6,
∴OP=OA=,
∴劣弧AP的长=.
10.【详解】(1)证明:∵四边形ADBC内接于⊙O,
∴∠EDA=∠ACB,
由圆周角定理得,∠CDA=∠ABC,
∵AD平分∠EDC,
∴∠EDA=∠CDA,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:连接AO并延长交BC于H,AM⊥CD于M,
∵AB=AC,四边形ADBC内接于⊙O,
∴AH⊥BC,又AH⊥AE,
∴AE∥BC,
∵CD为⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC=90°,
∴四边形AEBH为矩形,
∴BH=AE=2,
∴BC=4,
∵AD平分∠EDC,∠E=90°,AM⊥CD,
∴DE=DM=1,AE=AM=2,
在Rt△ABE和Rt△ACM中,
∴Rt△ABE≌Rt△ACM(HL),
∴BE=CM,
设BE=x,CD=x+2,
在Rt△BDC中,x2+42=(x+2)2,
解得,x=3,
∴CD=5,
∴⊙O的半径为2.5.
11.(2)
【详解】(1)连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠OBE,
∵EF∥AC,
∴∠CAE=∠FEA,
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB,
∵AB是的直径,
∴∠AEB=90°,
∴∠FEO=90°,
∴EF是切线;
(2)∵∠FEA=∠OEB=∠OBE,∠F=∠F,
∴ FEA~ FBE,
∴,
即:,
∴AF×(AF+15)=10×10,解得:AF=5或AF=-20(舍去),
∴,
∵在Rt ABE中,AE2+BE2=AB2,
∴AE2+(2AE)2=152,
∴AE=.
12.(2)π.
【详解】解:(1)连接AO.
∵∠ABC=45°,∴∠AOC=2∠B=90°.
∵OC∥AD,∴∠OAD=90°,
∴AD是⊙O的切线;
(2)连接OB.
∵∠BAD=105°,∠OAD=90°,
∴∠OAB=15°.
∵OB=OA,∴∠ABO=15°,
∴∠AOB=150°,
∴劣弧AB的长=.
13.(2)
【详解】(1)∵CF为直径,l为切线,
∴,
又∵,
∴CF//DE,
∴∠BCF=∠CDE.
又∠CED=∠CBF=90°,
∴;
(2)连接AF,
由题意得:∠CDP=∠BDM=45°,
∵M为弦AB的中点,
∴OM垂直平分线段AB,
∴∠ADM=∠BDM=45°,
∴△ADB为等腰直角三角形,
∴∠ADB=∠ADC=90°,
∴,
∵∠AFC=∠ABC=45°,
∴AC=CF×sin45°=,
∴.
14.【详解】(1)证明:连接OD
∵AB是⊙O的直径
∴
∴
∵
∴
∵
∴
∴
即PD⊥OD
∴直线PD为⊙O的切线;
(2)解:∵BE是⊙O的切线
∴
∵
∴
∵PD为⊙O的切线
∴
设⊙O的半径为
在Rt△PDO中,,则
∵
∴
解得
∴,
∴;
15.(2)
【详解】(1)∵EF=BD,
∴=
∴
∴∠D=∠DEF
又BD=BC,
∴∠D=∠C,
∴∠DEF=∠C
EF∥BC
(2)∵AB是直径,BC为切线,
∴AB⊥BC
又EF∥BC,
∴AB⊥EF,弧BF=弧BE,
GF=GE=(HF+EH)=3,HG=1
DB平分∠EDF,
又BF∥CD,
∴∠FBD=∠FDB=∠BDE=∠BFH
∴HB=HF=2
∴cos∠BHG==,∠BHG=60°.
∴∠FDB=∠BDE=30°
∴∠DFH=90°,DE为直径,DE=4,且弧BE所对圆心角=60°.
∴弧BE=×4=
答案第1页,共2页
同课章节目录
