2024年人教版数学中考复习专题训练:相似三角形与圆结合综合问题(含答案)
文档属性
| 名称 | 2024年人教版数学中考复习专题训练:相似三角形与圆结合综合问题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 00:00:00 | ||
图片预览



文档简介
2024年人教版数学中考复习专题训练:
相似三角形与圆结合综合问题
1.如图,点是的边上一点,以点为圆心,为半径作,与相切于点,连接,,交于点,连接并延长交的延长线于点,.
(1)求证:是的切线;
(2)若,,求的半径.
2.如图,是的直径,点F在上,的平分线交于点E,过点E作,交的延长线于点D,延长相交于点C.
(1)判断 与的位置关系,并说明理由;
(2)若的半径为5,,求的长.
3.如图,中,,点在外,是的弦,,连接若交于点,交于点,满足.
(1)求证:与相切;
(2)若,,求的长.
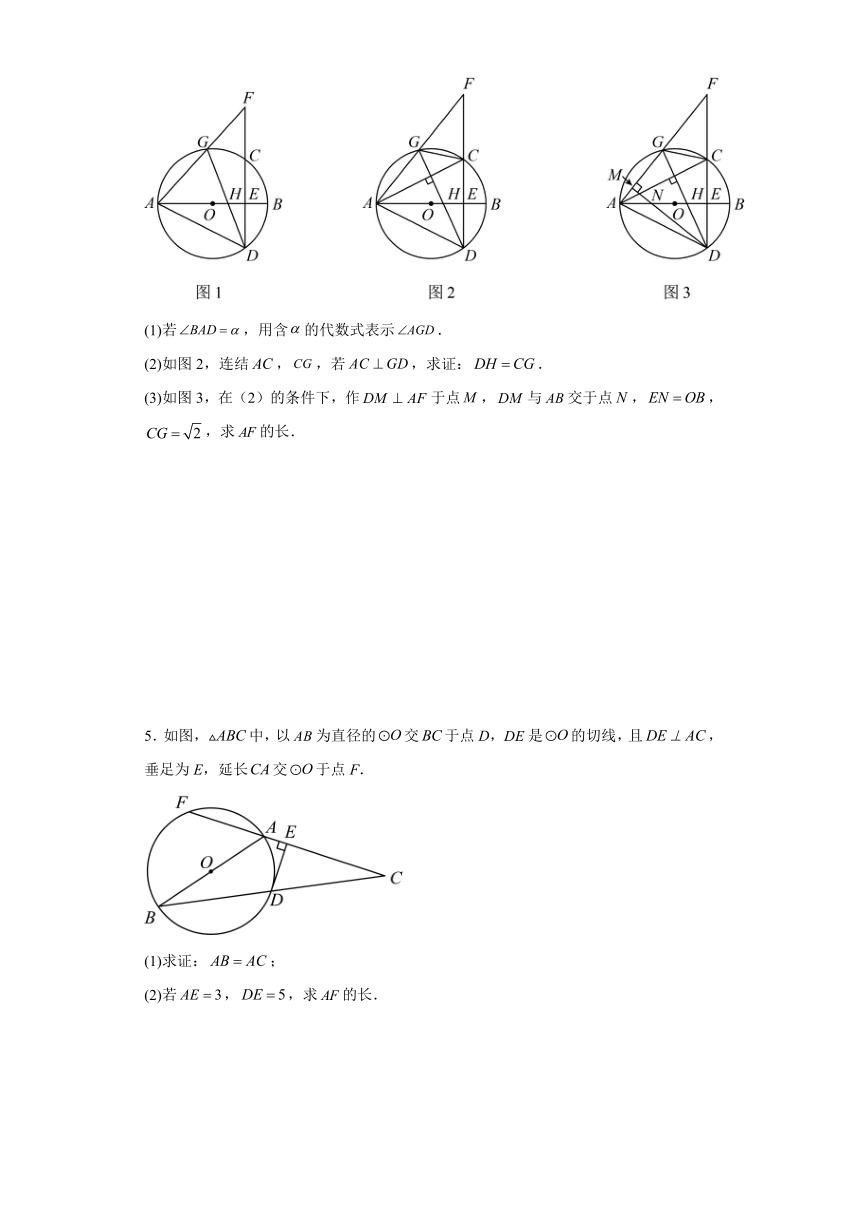
4.如图1,为的直径,弦于点,是上一点,延长,交于点,连结,,与交于点.
(1)若,用含的代数式表示.
(2)如图2,连结,,若,求证:.
(3)如图3,在(2)的条件下,作于点,与交于点,,,求的长.
5.如图,中,以为直径的交于点D,是的切线,且,垂足为E,延长交于点F.
(1)求证:;
(2)若,,求的长.
6.如图,在中,,平分,交于点D,以为直径作,交于点E,交于点F,连接交于点G,连接交于点P,连接.
(1)求证:是的切线;
(2)若,,求:
①的值;
②线段的长.
7.如图,内接于,是的直径,,过点A作,交于点E,点F是上一点,连接交于点G,连接交于点H.
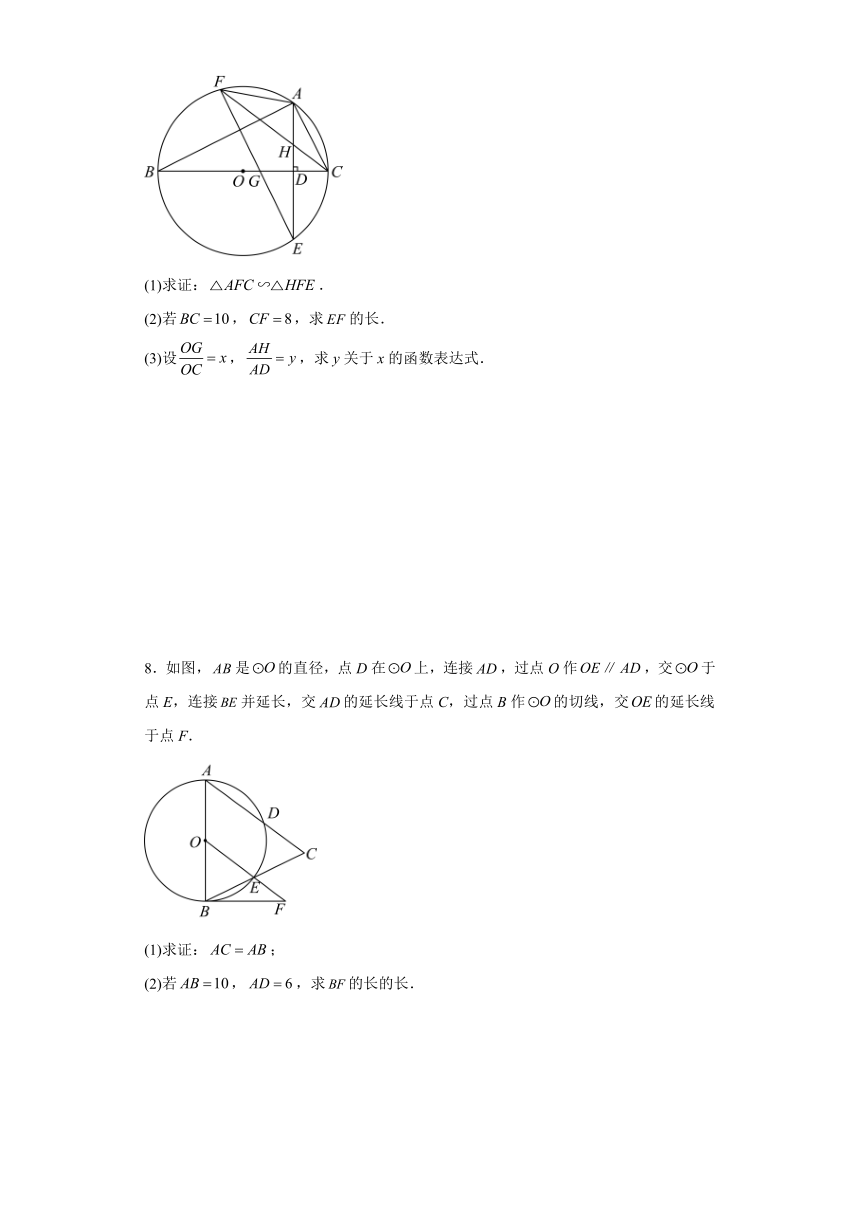
(1)求证:.
(2)若,,求的长.
(3)设,,求y关于x的函数表达式.
8.如图,是的直径,点D在上,连接,过点O作,交于点E,连接并延长,交的延长线于点C,过点B作的切线,交的延长线于点F.
(1)求证:;
(2)若,,求的长的长.
9.已知的半径为,P是外一点,,点A、B在上,在中,.
(1)如图①,是的切线,当时,求证:是的切线;
(2)如图②,、分别交于点C、D,当点C为中点时,求的长;
(3)线段的取值范围是______.
10.如图,在的内接四边形中,,直径,垂足为点F.
(1)当时,求的度数;
(2)当,时,求的长.
11.如图,以为直径的经过点,过点作的切线,交的延长线于点,,垂足为,交于点.
(1)求证:为等腰三角形;
(2)若,求的值.
12.如图,在中,,以为直径的交于点,交于点.
(1)求证:;
(2)若,求的长.
13.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理:如图(1),其原理是利用流动的河水,推动水车转动,水斗舀满河水,将水提升,等水斗转至顶空后再倾入接水槽,水流源源不断,流入田地,以利灌溉.如图(2),筒车圆O与水面分别交于点A、B,筒车上均匀分布着若干盛水筒,P表示筒车的一个盛水筒,接水槽所在的直线是圆O的切线,且与直线交于点M,当点P恰好在MN所在的直线上,P、O、C三点共线,是圆O的直径时,解决下面的问题:
(1)求证:;
(2)求证:;
(3)若,,,求的长.
14.已知、是圆的直径,于,连接.
(1)如图1,求证:.
(2)如图2,是上一点,,求证:.
(3)如图3,在(2)的条件下,连接,的延长线交于,若,.求的长.
15.如图1,是的外接圆,且满足,平分交于点、交于点.
(1)求证:;
(2)如图2,若点是的中点,求的度数;
(3)如图3,连接,若,
①求的值;
②若半径为,则_______.(用含的代数式表示)
参考答案:
1.(1)证明:在和中,
,
∴,
∴,
∵与相切,
∴,
∴,
即,
∵是的半径,
∴是的切线;
(2)解:在中,,
∴,
设圆O的半径为r,则
∴,
∵
∴
∵
∴
在中,
∴,
解得.
∴的半径为3.
2.(1)解:连接,
∵,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∴是的切线.
(2)解:如图,连接.
∵是的直径,
∴,
∵,
∴,
∴,
又∵
∴,
则.
又∵,
在中,,
即:,
解得,
则,
∴,
解得,.
∵,
∴,
∴,
设,
∴,解得:,
经检验:是原方程的解,
故的长为.
3.1)证明:,
,
,,
,
,
,
,
,
,
,
是的半径,且,
与相切.
(2)解:,,,
,,
,
,,
∽,
,
,
,
,
,
,
整理得,
解得或不符合题意,舍去,
,,
,
的长是.
4.(1)解:,
,
,
,
;
(2),,
,
,
,
,
,
;
(3)如图,连结,
,
,
,
,
,
,
,
,
,
,
,,
,
,
设,,
可得:,
解得:,
,
,
,
,
,
,
设,可得:,解得:,
,,
,
.
5.(1)如图所示,连接,
∵以为直径的交于点D,是的切线,
∴,
∵,
∴,
∴,
又,
∴,
∴,
∴;
(2)连接,,则,
∴
∴
∴
∴
∴即
∴
又∵是直径,
∴,
∴
∴
∴
∴
6.(1)证明:∵,平分,
∴,
∵是的半径,
∴是的切线;
(2)解:①连接,,,
∵为的直径,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,,
∴,
由垂径定理可得,
∴;
②∵,,
∴,
∴,
∴,
∴,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∴是等腰直角三角形,
∴.
7.(1)是的直径,,
,
,
和是所对圆周角,
,
.
(2)如图,连结,
是的直径,
,
,
,
,,
,
,
,
,
,
,
,
,
,
是的直径,
,
,,
,
,,
,
,
,
,
,
,
.
(3)设,则,
,
,,
,,
①如图,当点G在线段上时,
,
,,,
过点G作于点M,
,
,,
,
,
,
,
.
,
,即,
又,
,
,
,
,
.
②如图,当点G在线段上时,
同理可求得.
8.(1)解:,
,
,
,
.
(2)解:如图,连接,则,
,,
,.
是的切线,
,
,
,
,
,
即,
.
9.(1)连接,
∵是的切线,
,
在与中,
,
,
,
∵是的半径,
∴是的切线;
(2)连接,如图:
,点为中点,
,
∴是的直径,
设圆心为,
连接,
∵的半径为,
,
,
,
,
,即 ,
∴,
;
(3),
∴的运动轨迹为以为圆心,半径为的圆,如图:
∴三点共线时,最大, 此时,
即 ,
∴当最小时,最小,如图:
此时共线,,
,
作于,则 ,
, ,
,
,
故答案为:
10.(1)解:∵,
∴
∵直径,
∴,,
∵,
∴,
∴,
又∵,
∴.
(2)连接、交于点H,
∵,,
∴,,
∴,
在中,,由勾股定理得,
设半径为 r,则,
在中,,
由勾股定理得,即,
解之得:,
∴,
∵,
∴ ,
∴,即,
∴.
11.(1)证明:连接,
,
,
,
是的切线,
,
,
,
,
,
∴,
,
,
为等腰三角形;
(2)解:连接,
是的直径,
,
,
,
,
,
,
,
,
,
,
,
.
12.(1)证明:∵为的直径,
∴,
∴,
∵,
∴,
∴;
(2)解:连接,
∵,
∴,
∵,
而,
∴,
∴,即,
∴,
∴.
13.(1)证明:∵是的直径,
∴,
∴,
∵所在的直线是的切线,点恰好在所在的直线上,
∴,
∴,
∴,
∴,
∵,
∴.
(2)证明:∵,,
∴.
∴,
即.
(3)解:由(2)可知,
∵
,
∴,
.
14.(1)证明:如图1,连接,
是的直径,
,
,
,
,
,
,
,
;
(2)证明:如图2,延长交于,连接、、,
,
∴,是的中垂线,
∴,
,
,
∵,
∴四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,,
∵,
∴;
(3)解:如图3,连接,设,
∵,
∴,
∴,
∵,
∴,即,
整理得,
解得(舍去),或,
∴,
∴,,
,
,
,
∴,
,
,
,
.
15.(1)证明:如图,
平分,
,
,
,
;
(2)解:如图,
平分,
,
点是的中点,
,
,
设,则,
∴;
,
∴;
在中,则有,
即,
∴,
∴;
(3)解:如图,
设,
,
∴,,
∵,,
∴,
∴,
即,
∴;
设,则,
∵,
∴;
∵,,
∴,
∴,
∴,
∴;
∵,
∴,
∴,即;
∵,
∴,
.
如图,连接并延长交于F,连接,
∵,
∴是线段的垂直平分线,
∴;
∵平分,
∴点D到的距离相等,且设这个距离为d,
∴;
∵,
∴;
由①知,,则;
在中,由勾股定理得:,
∴,
在中,由勾股定理得:,
解得:;
∵,
∴;
∵,
∴.
故答案为:.
相似三角形与圆结合综合问题
1.如图,点是的边上一点,以点为圆心,为半径作,与相切于点,连接,,交于点,连接并延长交的延长线于点,.
(1)求证:是的切线;
(2)若,,求的半径.
2.如图,是的直径,点F在上,的平分线交于点E,过点E作,交的延长线于点D,延长相交于点C.
(1)判断 与的位置关系,并说明理由;
(2)若的半径为5,,求的长.
3.如图,中,,点在外,是的弦,,连接若交于点,交于点,满足.
(1)求证:与相切;
(2)若,,求的长.
4.如图1,为的直径,弦于点,是上一点,延长,交于点,连结,,与交于点.
(1)若,用含的代数式表示.
(2)如图2,连结,,若,求证:.
(3)如图3,在(2)的条件下,作于点,与交于点,,,求的长.
5.如图,中,以为直径的交于点D,是的切线,且,垂足为E,延长交于点F.
(1)求证:;
(2)若,,求的长.
6.如图,在中,,平分,交于点D,以为直径作,交于点E,交于点F,连接交于点G,连接交于点P,连接.
(1)求证:是的切线;
(2)若,,求:
①的值;
②线段的长.
7.如图,内接于,是的直径,,过点A作,交于点E,点F是上一点,连接交于点G,连接交于点H.
(1)求证:.
(2)若,,求的长.
(3)设,,求y关于x的函数表达式.
8.如图,是的直径,点D在上,连接,过点O作,交于点E,连接并延长,交的延长线于点C,过点B作的切线,交的延长线于点F.
(1)求证:;
(2)若,,求的长的长.
9.已知的半径为,P是外一点,,点A、B在上,在中,.
(1)如图①,是的切线,当时,求证:是的切线;
(2)如图②,、分别交于点C、D,当点C为中点时,求的长;
(3)线段的取值范围是______.
10.如图,在的内接四边形中,,直径,垂足为点F.
(1)当时,求的度数;
(2)当,时,求的长.
11.如图,以为直径的经过点,过点作的切线,交的延长线于点,,垂足为,交于点.
(1)求证:为等腰三角形;
(2)若,求的值.
12.如图,在中,,以为直径的交于点,交于点.
(1)求证:;
(2)若,求的长.
13.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理:如图(1),其原理是利用流动的河水,推动水车转动,水斗舀满河水,将水提升,等水斗转至顶空后再倾入接水槽,水流源源不断,流入田地,以利灌溉.如图(2),筒车圆O与水面分别交于点A、B,筒车上均匀分布着若干盛水筒,P表示筒车的一个盛水筒,接水槽所在的直线是圆O的切线,且与直线交于点M,当点P恰好在MN所在的直线上,P、O、C三点共线,是圆O的直径时,解决下面的问题:
(1)求证:;
(2)求证:;
(3)若,,,求的长.
14.已知、是圆的直径,于,连接.
(1)如图1,求证:.
(2)如图2,是上一点,,求证:.
(3)如图3,在(2)的条件下,连接,的延长线交于,若,.求的长.
15.如图1,是的外接圆,且满足,平分交于点、交于点.
(1)求证:;
(2)如图2,若点是的中点,求的度数;
(3)如图3,连接,若,
①求的值;
②若半径为,则_______.(用含的代数式表示)
参考答案:
1.(1)证明:在和中,
,
∴,
∴,
∵与相切,
∴,
∴,
即,
∵是的半径,
∴是的切线;
(2)解:在中,,
∴,
设圆O的半径为r,则
∴,
∵
∴
∵
∴
在中,
∴,
解得.
∴的半径为3.
2.(1)解:连接,
∵,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∴是的切线.
(2)解:如图,连接.
∵是的直径,
∴,
∵,
∴,
∴,
又∵
∴,
则.
又∵,
在中,,
即:,
解得,
则,
∴,
解得,.
∵,
∴,
∴,
设,
∴,解得:,
经检验:是原方程的解,
故的长为.
3.1)证明:,
,
,,
,
,
,
,
,
,
,
是的半径,且,
与相切.
(2)解:,,,
,,
,
,,
∽,
,
,
,
,
,
,
整理得,
解得或不符合题意,舍去,
,,
,
的长是.
4.(1)解:,
,
,
,
;
(2),,
,
,
,
,
,
;
(3)如图,连结,
,
,
,
,
,
,
,
,
,
,
,,
,
,
设,,
可得:,
解得:,
,
,
,
,
,
,
设,可得:,解得:,
,,
,
.
5.(1)如图所示,连接,
∵以为直径的交于点D,是的切线,
∴,
∵,
∴,
∴,
又,
∴,
∴,
∴;
(2)连接,,则,
∴
∴
∴
∴
∴即
∴
又∵是直径,
∴,
∴
∴
∴
∴
6.(1)证明:∵,平分,
∴,
∵是的半径,
∴是的切线;
(2)解:①连接,,,
∵为的直径,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,,
∴,
由垂径定理可得,
∴;
②∵,,
∴,
∴,
∴,
∴,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∴是等腰直角三角形,
∴.
7.(1)是的直径,,
,
,
和是所对圆周角,
,
.
(2)如图,连结,
是的直径,
,
,
,
,,
,
,
,
,
,
,
,
,
,
是的直径,
,
,,
,
,,
,
,
,
,
,
,
.
(3)设,则,
,
,,
,,
①如图,当点G在线段上时,
,
,,,
过点G作于点M,
,
,,
,
,
,
,
.
,
,即,
又,
,
,
,
,
.
②如图,当点G在线段上时,
同理可求得.
8.(1)解:,
,
,
,
.
(2)解:如图,连接,则,
,,
,.
是的切线,
,
,
,
,
,
即,
.
9.(1)连接,
∵是的切线,
,
在与中,
,
,
,
∵是的半径,
∴是的切线;
(2)连接,如图:
,点为中点,
,
∴是的直径,
设圆心为,
连接,
∵的半径为,
,
,
,
,
,即 ,
∴,
;
(3),
∴的运动轨迹为以为圆心,半径为的圆,如图:
∴三点共线时,最大, 此时,
即 ,
∴当最小时,最小,如图:
此时共线,,
,
作于,则 ,
, ,
,
,
故答案为:
10.(1)解:∵,
∴
∵直径,
∴,,
∵,
∴,
∴,
又∵,
∴.
(2)连接、交于点H,
∵,,
∴,,
∴,
在中,,由勾股定理得,
设半径为 r,则,
在中,,
由勾股定理得,即,
解之得:,
∴,
∵,
∴ ,
∴,即,
∴.
11.(1)证明:连接,
,
,
,
是的切线,
,
,
,
,
,
∴,
,
,
为等腰三角形;
(2)解:连接,
是的直径,
,
,
,
,
,
,
,
,
,
,
,
.
12.(1)证明:∵为的直径,
∴,
∴,
∵,
∴,
∴;
(2)解:连接,
∵,
∴,
∵,
而,
∴,
∴,即,
∴,
∴.
13.(1)证明:∵是的直径,
∴,
∴,
∵所在的直线是的切线,点恰好在所在的直线上,
∴,
∴,
∴,
∴,
∵,
∴.
(2)证明:∵,,
∴.
∴,
即.
(3)解:由(2)可知,
∵
,
∴,
.
14.(1)证明:如图1,连接,
是的直径,
,
,
,
,
,
,
,
;
(2)证明:如图2,延长交于,连接、、,
,
∴,是的中垂线,
∴,
,
,
∵,
∴四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,,
∵,
∴;
(3)解:如图3,连接,设,
∵,
∴,
∴,
∵,
∴,即,
整理得,
解得(舍去),或,
∴,
∴,,
,
,
,
∴,
,
,
,
.
15.(1)证明:如图,
平分,
,
,
,
;
(2)解:如图,
平分,
,
点是的中点,
,
,
设,则,
∴;
,
∴;
在中,则有,
即,
∴,
∴;
(3)解:如图,
设,
,
∴,,
∵,,
∴,
∴,
即,
∴;
设,则,
∵,
∴;
∵,,
∴,
∴,
∴,
∴;
∵,
∴,
∴,即;
∵,
∴,
.
如图,连接并延长交于F,连接,
∵,
∴是线段的垂直平分线,
∴;
∵平分,
∴点D到的距离相等,且设这个距离为d,
∴;
∵,
∴;
由①知,,则;
在中,由勾股定理得:,
∴,
在中,由勾股定理得:,
解得:;
∵,
∴;
∵,
∴.
故答案为:.
同课章节目录
