2023-2024学年广西贵港市高二(上)期末数学试卷 (含解析)
文档属性
| 名称 | 2023-2024学年广西贵港市高二(上)期末数学试卷 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 90.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 09:03:27 | ||
图片预览




文档简介
2023-2024学年广西贵港市高二(上)期末数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.复数在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.在数列中,已知,,若,则( )
A. B. C. D.
4.已知为第四象限角,且,则( )
A. B. C. D.
5.过抛物线:的焦点的直线与抛物线相交于,两点,若线段中点的坐标为,则( )
A. B. C. D.
6.苏格兰数学家纳皮尔在研究天文学的过程中,为了简化其中的大数之间的计算而发明了对数利用对数运算可以求大数的位数已知,则是( )
A. 位数 B. 位数 C. 位数 D. 位数
7.如图,三角形蜘蛛网是由一些正三角形环绕而成的图形,每个正三角形的顶点都是其外接正三角形各边的中点现有米长的铁丝材料用来制作一个网格数最多的三角形蜘蛛网,若该三角形蜘蛛网中最大的正三角形的边长为米,则最小的正三角形的边长为( )
A. 米 B. 米 C. 米 D. 米
8.如图,椭圆:的左、右焦点分别为,,为椭圆上一点,为轴上一点,在以为直径的圆上,且,则椭圆的离心率为( )
A.
B.
C.
D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.等差数列的前项和为,若,,则( )
A. 的公差为 B. 的公差为 C. D.
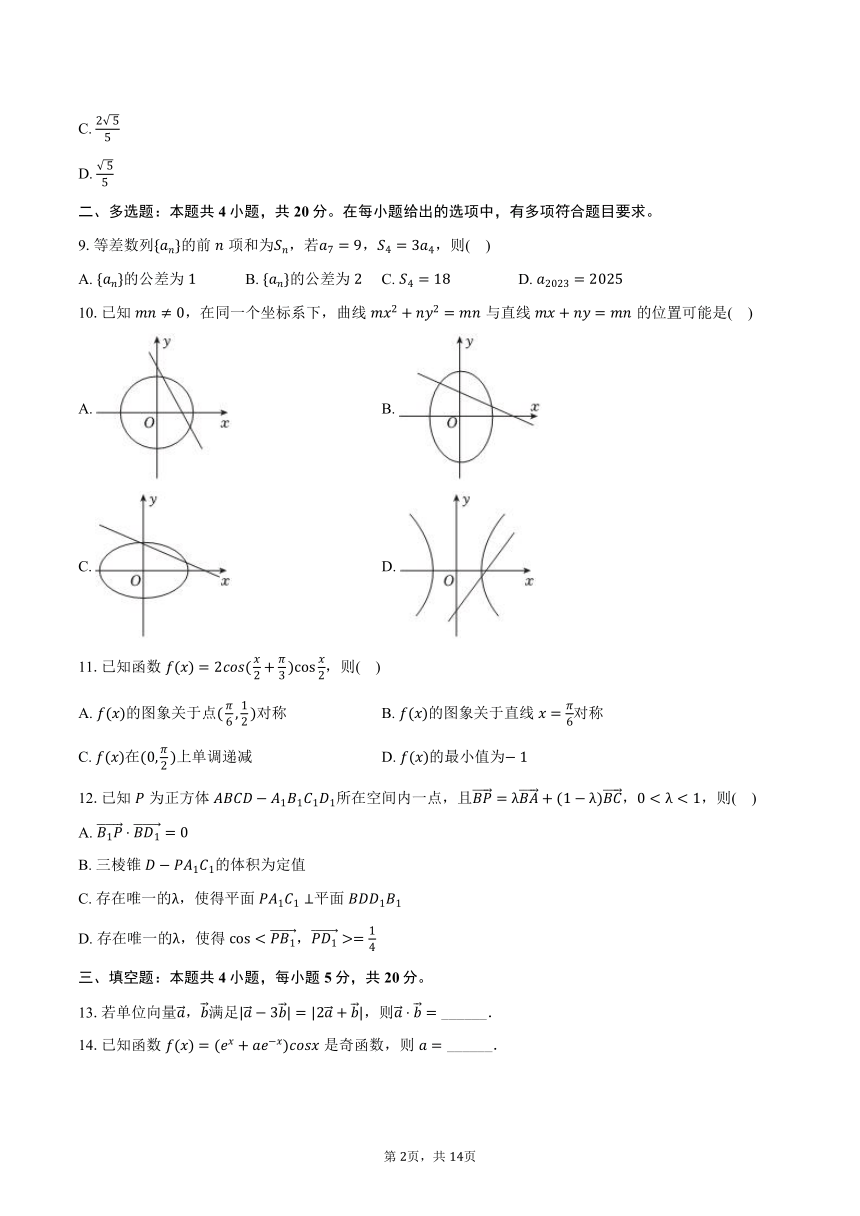
10.已知,在同一个坐标系下,曲线与直线的位置可能是( )
A. B.
C. D.
11.已知函数,则( )
A. 的图象关于点对称 B. 的图象关于直线对称
C. 在上单调递减 D. 的最小值为
12.已知为正方体所在空间内一点,且,,则( )
A.
B. 三棱锥的体积为定值
C. 存在唯一的,使得平面平面
D. 存在唯一的,使得,
三、填空题:本题共4小题,每小题5分,共20分。
13.若单位向量,满足,则 ______.
14.已知函数是奇函数,则 ______.
15.若直线是圆的一条对称轴,则点与该圆上任意一点的距离的最小值为______.
16.若,是函数的两个不同的零点,且,,这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 ______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
的内角,,的对边分别为,,,已知,.
求的值;
若,求的面积.
18.本小题分
已知四边形的三个顶点,,.
求过,,三点的圆的方程.
设线段上靠近点的三等分点为,过的直线平分四边形的面积若四边形为平行四边形,求直线的方程.
19.本小题分
杭州亚运会期同,某大学有名学生参加体育成绩测评,将他们的分数单位:分按照,,,,分成五组,绘制成如图所示的频率分布直方图.
求的值及这组数据的第百分位数;
按分层陆机抽样的方法从分数在和内的学生中抽取人,再从这人中任选人,求这人成绩之差的绝对值大于分的概率.
20.本小题分
如图,在三棱锥中,平面,,,是的中点,且.
求的长;
求二面角的正弦值.
21.本小题分
已知数列的前项和满足.
求的通项公式;
求数列的前项和.
22.本小题分
已知椭圆与双曲线的焦距之比为.
求椭圆和双曲线的离心率;
设双曲线的右焦点为,过作轴交双曲线于点在第一象限,,分别为椭圆的左、右顶点,与椭圆交于另一点,为坐标原点,证明:.
答案和解析
1.【答案】
【解析】解:根据题意,可得,
因为,所以.
故选:.
根据题意,先确定出集合的元素,再根据交集的运算法则算出答案.
本题主要考查集合的概念与表示、交集的运算法则等知识,属于基础题.
2.【答案】
【解析】解:,
复数在复平面内对应的点位于第一象限.
故选:.
利用复数的运算法则、几何意义直接求解.
本题考查复数的运算法则、几何意义等基础知识,考查运算求解能力,是基础题.
3.【答案】
【解析】解:因为,所以,
两边取倒数,可得,
则是首项为,公差为的等差数列,
可得,即,
由,
解得.
故选:.
对已知递推式两边同时取倒数,由等差数列的通项公式,解方程可得所求值.
本题考查数列的递推式和等差数列的通项公式,考查运算能力,属于基础题.
4.【答案】
【解析】解:由题意,,又,联立可得.
又为第四象限角,则.
故选:.
根据同角三角函数的关系求解.
本题考查同角三角函数的关系,属于基础题.
5.【答案】
【解析】解:设,,
因为点,在抛物线上,可得,两式作差可得.
因为线段中点的坐标为,所以,解得.
故选:.
设,,利用作差法可得,求解即可.
本题考查抛物线的性质,考查作差法的应用,属基础题.
6.【答案】
【解析】解:记,则,
则,则,
故是位数.
故选:.
利用及指数与对数的转化计算即可.
本题主要考查了对数运算性质,属于基础题.
7.【答案】
【解析】解:如图,三角形蜘蛛网是由一些正三角形环绕而成的图形,
每个正三角形的顶点都是其外接正三角形各边的中点,
现有米长的铁丝材料用来制作一个网格数最多的三角形蜘蛛网,
该三角形蜘蛛网中最大的正三角形的边长为米,
由题可知,该三角形蜘蛛网中三角形的周长从大到小是以为首项,为公比的等比数列,
设最小的正三角形的边长为米,则,则,得,
故最小的正三角形的边长为米.
故选:.
利用等比数列的性质求解.
本题考查等比数列的性质等基础知识,考查运算求解能力,是基础题.
8.【答案】
【解析】解:由,设,,,
则,由对称性知,,
因为在以为直径的圆上,则,,
由椭圆的定义知,所以,
在中,,
所以,所以.
故选:.
由,设,,,由椭圆的定义及在以为直径的圆上,得,再结合余弦定理求出,即可求出离心率.
本题考查椭圆的性质,属中档题.
9.【答案】
【解析】解:设的公差为,
,,
则解得
故,.
故选:.
根据已知条件,结合等差数列的前项和公式,以及等差数列的性质,即可求解.
本题主要考查等差数列的前项和公式,以及等差数列的性质,属于基础题.
10.【答案】
【解析】解:因为,所以曲线与直线可化为曲线与直线.
当时,曲线表示的是圆,直线的横截距与纵截距相等.不正确.
当时,曲线表示焦点在轴上的椭圆,直线的横截距比纵截距小.不正确.
当时,曲线表示焦点在轴上的椭圆,直线的横截距比纵截距大.C正确.
当时,曲线表示焦点在轴上的双曲线,直线的横截距为正,纵截距为负.D正确.
故选:.
先将方程转化为标准方程,结合直线截距,斜率以及椭圆双曲线中,的符号,判断是否对应即可.
本题主要考查图象的识别和判断,结合圆锥曲线中,,的符号以及直线斜率和截距的关系是否对应是解决本题的关键.是中档题.
11.【答案】
【解析】解:,
当时,,
的图象关于点对称,故 A正确,不正确;
当时,,
在上单调递减,故 C正确;
又的最小值为,故D不正确.
故选:.
化简得,利用余弦函数的性质对各个选项逐一分析可得答案.
本题考查余弦函数的奇偶性、对称性、单调性等性质的综合应用,属于中档题.
12.【答案】
【解析】 解:建立空间直角坐标系,如图所示:
因为,,所以为线段内的点,
设,;
,
,
所以,选项A错误;
三棱锥的体积为,是定值,选项B正确;
当且仅当为的中点时,平面平面,此时,选项C正确;
因为,
,
所以,
;
令,化简得,,所以方程无解,
即不存在,使,,选项D错误.
故选:.
建立空间直角坐标系,利用坐标表示向量,根据,,得出为线段内的点,可设,,由此求解判断即可.
本题考查了空间向量的应用问题,也考查了推理与判断能力,是中档题.
13.【答案】
【解析】解:因为、是单位向量,所以,
又因为,所以,
解得.
故答案为:.
根据平面向量的数量积与模长公式,计算即可.
本题考查了平面向量的数量积与模长计算问题,是基础题.
14.【答案】
【解析】解:因为是奇函数,
所以,
即,
则.
故答案为:.
由已知结合奇函数的定义即可求解.
本题主要考查了奇函数定义的应用,属于基础题.
15.【答案】
【解析】解:由题可知,该圆的圆心为,
因为直线过圆心,所以,解得,
所以圆的方程为,
因为圆心与的距离为,
所以点与该圆上任意一点的距离的最小值为.
故答案为:.
根据题意求出圆的方程,求出圆心到点的距离与半径的差即可.
本题考查直线与圆的位置关系,属基础题.
16.【答案】
【解析】解:由题可知,,则,
因为,,这三个数可适当排序后成等比数列,
则必是等比中项,则,
又,,这三个数可适当排序后成等差数列,则必不是等差中项,
若是等差中项,则,
解得,,则,
故,
若是等差中项,则,又,
解得,,
则,
故.
故答案为:.
由韦达定理求出,,,之间的关系,然后由,,这三个数可适当排序后成等差数列,也可适当排序后成等比数列,分类讨论求解即可.
本题主要考查了等比数列和等差数列的性质,属于基础题.
17.【答案】解:,,则.
又,所以.
,,
则,
故的面积.
【解析】利用正弦定理求解;
利用余弦定理与三角形的面积公式求解.
本题考查正余弦定理的应用,属于基础题.
18.【答案】解:因为,,,所以,.
由,得,
则过,,三点的圆的圆心为线段的中点,半径,
则过,,三点的圆的方程为.
因为四边形为平行四边形,所以.
因为线段上靠近点的三等分点为,所以,则.
设与相交于点,由直线平分四边形的面积,可得,则.
则的方程为,整理得.
【解析】结合直线的斜率公式,以及直线垂直的性质,两点之间的距离公式,即可求解;
结合平面向量的坐标运算,以及求出点,再结合直线的点斜式方程,即可求解.
本题主要考查直线与圆的位置关系,考查转化能力,属于中档题.
19.【答案】解:由频率分布直方图可知,,
解得,
因为,,
所以这组数据的第百分位数位于,设其为,
则,
解得;
由题可知,从分数在内的学生中抽取人,记为,,
则分数在内的人数为,记为,,,,
从中任选人,样本空间,,,,,,,,
,,,,,,,
这人成绩之差的绝对值大于分的样本空间,,,,,,,,
故所求的概率.
【解析】利用频率分布直方图中各个小矩形的面积之和为可求出的值,再利用百分位数的定义求这组数据的第百分位数即可;
利用古典概型的概率公式求解.
本题主要考查了频率分布直方图的应用,考查了古典概型的概率公式,属于中档题.
20.【答案】解:因为平面,,过作平行于的直线,
所以以为坐标原点,,,所在直线分别为,,轴,建立如图所示的空间直角坐标系.
设,由,得,,,.
因为是的中点,所以,
所以,,
又因为,所以,
解得,所以;
由可知,,
所以,,,
设平面的法向量为,
则,即
解得,令,得,所以.
设平面的法向量为,
则,即
令,得,,所以.
因为,
所以二面角的正弦值为.
【解析】建立空间直角坐标系,设,由建立方程,求解即可;
求出平面和平面的法向量,由向量的夹角公式计算即可.
本题考查二面角的求法,属于中档题.
21.【答案】解:当时,,
当时,由,得,
则,
因为,
所以;
由可知,,
则,
则,
则
,
所以.
【解析】由已知结合数列的和与项的递推关系即可求解;
先求数列的通项公式,然后利用错位相减求和即可求解.
本题主要考查了数列的和与项的递推关系在数列通项公式求解中的应用,还考查了错位相减求和,属于中档题.
22.【答案】解:易知椭圆的焦距,双曲线的焦距,
因为椭圆与双曲线的焦距之比为,
所以,
整理得,
此时,,
则椭圆的离心率,双曲线的离心率,
证明:由知,
因为,
此时直线的方程为,
联立,消去并整理得,
由韦达定理得,
解得,
则,
因为,,,
所以,,
故.
【解析】由题意,根据题目所给信息以及椭圆和双曲线的性质,列出等式进行求解即可;
结合中信息得到点的坐标,将直线的方程与椭圆方程联立,利用韦达定理求出点的坐标,根据斜率公式再进行求证即可.
本题考查椭圆的性质以及直线与圆锥曲线的综合问题,考查了逻辑推理和运算能力,属于中档题.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.复数在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.在数列中,已知,,若,则( )
A. B. C. D.
4.已知为第四象限角,且,则( )
A. B. C. D.
5.过抛物线:的焦点的直线与抛物线相交于,两点,若线段中点的坐标为,则( )
A. B. C. D.
6.苏格兰数学家纳皮尔在研究天文学的过程中,为了简化其中的大数之间的计算而发明了对数利用对数运算可以求大数的位数已知,则是( )
A. 位数 B. 位数 C. 位数 D. 位数
7.如图,三角形蜘蛛网是由一些正三角形环绕而成的图形,每个正三角形的顶点都是其外接正三角形各边的中点现有米长的铁丝材料用来制作一个网格数最多的三角形蜘蛛网,若该三角形蜘蛛网中最大的正三角形的边长为米,则最小的正三角形的边长为( )
A. 米 B. 米 C. 米 D. 米
8.如图,椭圆:的左、右焦点分别为,,为椭圆上一点,为轴上一点,在以为直径的圆上,且,则椭圆的离心率为( )
A.
B.
C.
D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.等差数列的前项和为,若,,则( )
A. 的公差为 B. 的公差为 C. D.
10.已知,在同一个坐标系下,曲线与直线的位置可能是( )
A. B.
C. D.
11.已知函数,则( )
A. 的图象关于点对称 B. 的图象关于直线对称
C. 在上单调递减 D. 的最小值为
12.已知为正方体所在空间内一点,且,,则( )
A.
B. 三棱锥的体积为定值
C. 存在唯一的,使得平面平面
D. 存在唯一的,使得,
三、填空题:本题共4小题,每小题5分,共20分。
13.若单位向量,满足,则 ______.
14.已知函数是奇函数,则 ______.
15.若直线是圆的一条对称轴,则点与该圆上任意一点的距离的最小值为______.
16.若,是函数的两个不同的零点,且,,这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 ______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
的内角,,的对边分别为,,,已知,.
求的值;
若,求的面积.
18.本小题分
已知四边形的三个顶点,,.
求过,,三点的圆的方程.
设线段上靠近点的三等分点为,过的直线平分四边形的面积若四边形为平行四边形,求直线的方程.
19.本小题分
杭州亚运会期同,某大学有名学生参加体育成绩测评,将他们的分数单位:分按照,,,,分成五组,绘制成如图所示的频率分布直方图.
求的值及这组数据的第百分位数;
按分层陆机抽样的方法从分数在和内的学生中抽取人,再从这人中任选人,求这人成绩之差的绝对值大于分的概率.
20.本小题分
如图,在三棱锥中,平面,,,是的中点,且.
求的长;
求二面角的正弦值.
21.本小题分
已知数列的前项和满足.
求的通项公式;
求数列的前项和.
22.本小题分
已知椭圆与双曲线的焦距之比为.
求椭圆和双曲线的离心率;
设双曲线的右焦点为,过作轴交双曲线于点在第一象限,,分别为椭圆的左、右顶点,与椭圆交于另一点,为坐标原点,证明:.
答案和解析
1.【答案】
【解析】解:根据题意,可得,
因为,所以.
故选:.
根据题意,先确定出集合的元素,再根据交集的运算法则算出答案.
本题主要考查集合的概念与表示、交集的运算法则等知识,属于基础题.
2.【答案】
【解析】解:,
复数在复平面内对应的点位于第一象限.
故选:.
利用复数的运算法则、几何意义直接求解.
本题考查复数的运算法则、几何意义等基础知识,考查运算求解能力,是基础题.
3.【答案】
【解析】解:因为,所以,
两边取倒数,可得,
则是首项为,公差为的等差数列,
可得,即,
由,
解得.
故选:.
对已知递推式两边同时取倒数,由等差数列的通项公式,解方程可得所求值.
本题考查数列的递推式和等差数列的通项公式,考查运算能力,属于基础题.
4.【答案】
【解析】解:由题意,,又,联立可得.
又为第四象限角,则.
故选:.
根据同角三角函数的关系求解.
本题考查同角三角函数的关系,属于基础题.
5.【答案】
【解析】解:设,,
因为点,在抛物线上,可得,两式作差可得.
因为线段中点的坐标为,所以,解得.
故选:.
设,,利用作差法可得,求解即可.
本题考查抛物线的性质,考查作差法的应用,属基础题.
6.【答案】
【解析】解:记,则,
则,则,
故是位数.
故选:.
利用及指数与对数的转化计算即可.
本题主要考查了对数运算性质,属于基础题.
7.【答案】
【解析】解:如图,三角形蜘蛛网是由一些正三角形环绕而成的图形,
每个正三角形的顶点都是其外接正三角形各边的中点,
现有米长的铁丝材料用来制作一个网格数最多的三角形蜘蛛网,
该三角形蜘蛛网中最大的正三角形的边长为米,
由题可知,该三角形蜘蛛网中三角形的周长从大到小是以为首项,为公比的等比数列,
设最小的正三角形的边长为米,则,则,得,
故最小的正三角形的边长为米.
故选:.
利用等比数列的性质求解.
本题考查等比数列的性质等基础知识,考查运算求解能力,是基础题.
8.【答案】
【解析】解:由,设,,,
则,由对称性知,,
因为在以为直径的圆上,则,,
由椭圆的定义知,所以,
在中,,
所以,所以.
故选:.
由,设,,,由椭圆的定义及在以为直径的圆上,得,再结合余弦定理求出,即可求出离心率.
本题考查椭圆的性质,属中档题.
9.【答案】
【解析】解:设的公差为,
,,
则解得
故,.
故选:.
根据已知条件,结合等差数列的前项和公式,以及等差数列的性质,即可求解.
本题主要考查等差数列的前项和公式,以及等差数列的性质,属于基础题.
10.【答案】
【解析】解:因为,所以曲线与直线可化为曲线与直线.
当时,曲线表示的是圆,直线的横截距与纵截距相等.不正确.
当时,曲线表示焦点在轴上的椭圆,直线的横截距比纵截距小.不正确.
当时,曲线表示焦点在轴上的椭圆,直线的横截距比纵截距大.C正确.
当时,曲线表示焦点在轴上的双曲线,直线的横截距为正,纵截距为负.D正确.
故选:.
先将方程转化为标准方程,结合直线截距,斜率以及椭圆双曲线中,的符号,判断是否对应即可.
本题主要考查图象的识别和判断,结合圆锥曲线中,,的符号以及直线斜率和截距的关系是否对应是解决本题的关键.是中档题.
11.【答案】
【解析】解:,
当时,,
的图象关于点对称,故 A正确,不正确;
当时,,
在上单调递减,故 C正确;
又的最小值为,故D不正确.
故选:.
化简得,利用余弦函数的性质对各个选项逐一分析可得答案.
本题考查余弦函数的奇偶性、对称性、单调性等性质的综合应用,属于中档题.
12.【答案】
【解析】 解:建立空间直角坐标系,如图所示:
因为,,所以为线段内的点,
设,;
,
,
所以,选项A错误;
三棱锥的体积为,是定值,选项B正确;
当且仅当为的中点时,平面平面,此时,选项C正确;
因为,
,
所以,
;
令,化简得,,所以方程无解,
即不存在,使,,选项D错误.
故选:.
建立空间直角坐标系,利用坐标表示向量,根据,,得出为线段内的点,可设,,由此求解判断即可.
本题考查了空间向量的应用问题,也考查了推理与判断能力,是中档题.
13.【答案】
【解析】解:因为、是单位向量,所以,
又因为,所以,
解得.
故答案为:.
根据平面向量的数量积与模长公式,计算即可.
本题考查了平面向量的数量积与模长计算问题,是基础题.
14.【答案】
【解析】解:因为是奇函数,
所以,
即,
则.
故答案为:.
由已知结合奇函数的定义即可求解.
本题主要考查了奇函数定义的应用,属于基础题.
15.【答案】
【解析】解:由题可知,该圆的圆心为,
因为直线过圆心,所以,解得,
所以圆的方程为,
因为圆心与的距离为,
所以点与该圆上任意一点的距离的最小值为.
故答案为:.
根据题意求出圆的方程,求出圆心到点的距离与半径的差即可.
本题考查直线与圆的位置关系,属基础题.
16.【答案】
【解析】解:由题可知,,则,
因为,,这三个数可适当排序后成等比数列,
则必是等比中项,则,
又,,这三个数可适当排序后成等差数列,则必不是等差中项,
若是等差中项,则,
解得,,则,
故,
若是等差中项,则,又,
解得,,
则,
故.
故答案为:.
由韦达定理求出,,,之间的关系,然后由,,这三个数可适当排序后成等差数列,也可适当排序后成等比数列,分类讨论求解即可.
本题主要考查了等比数列和等差数列的性质,属于基础题.
17.【答案】解:,,则.
又,所以.
,,
则,
故的面积.
【解析】利用正弦定理求解;
利用余弦定理与三角形的面积公式求解.
本题考查正余弦定理的应用,属于基础题.
18.【答案】解:因为,,,所以,.
由,得,
则过,,三点的圆的圆心为线段的中点,半径,
则过,,三点的圆的方程为.
因为四边形为平行四边形,所以.
因为线段上靠近点的三等分点为,所以,则.
设与相交于点,由直线平分四边形的面积,可得,则.
则的方程为,整理得.
【解析】结合直线的斜率公式,以及直线垂直的性质,两点之间的距离公式,即可求解;
结合平面向量的坐标运算,以及求出点,再结合直线的点斜式方程,即可求解.
本题主要考查直线与圆的位置关系,考查转化能力,属于中档题.
19.【答案】解:由频率分布直方图可知,,
解得,
因为,,
所以这组数据的第百分位数位于,设其为,
则,
解得;
由题可知,从分数在内的学生中抽取人,记为,,
则分数在内的人数为,记为,,,,
从中任选人,样本空间,,,,,,,,
,,,,,,,
这人成绩之差的绝对值大于分的样本空间,,,,,,,,
故所求的概率.
【解析】利用频率分布直方图中各个小矩形的面积之和为可求出的值,再利用百分位数的定义求这组数据的第百分位数即可;
利用古典概型的概率公式求解.
本题主要考查了频率分布直方图的应用,考查了古典概型的概率公式,属于中档题.
20.【答案】解:因为平面,,过作平行于的直线,
所以以为坐标原点,,,所在直线分别为,,轴,建立如图所示的空间直角坐标系.
设,由,得,,,.
因为是的中点,所以,
所以,,
又因为,所以,
解得,所以;
由可知,,
所以,,,
设平面的法向量为,
则,即
解得,令,得,所以.
设平面的法向量为,
则,即
令,得,,所以.
因为,
所以二面角的正弦值为.
【解析】建立空间直角坐标系,设,由建立方程,求解即可;
求出平面和平面的法向量,由向量的夹角公式计算即可.
本题考查二面角的求法,属于中档题.
21.【答案】解:当时,,
当时,由,得,
则,
因为,
所以;
由可知,,
则,
则,
则
,
所以.
【解析】由已知结合数列的和与项的递推关系即可求解;
先求数列的通项公式,然后利用错位相减求和即可求解.
本题主要考查了数列的和与项的递推关系在数列通项公式求解中的应用,还考查了错位相减求和,属于中档题.
22.【答案】解:易知椭圆的焦距,双曲线的焦距,
因为椭圆与双曲线的焦距之比为,
所以,
整理得,
此时,,
则椭圆的离心率,双曲线的离心率,
证明:由知,
因为,
此时直线的方程为,
联立,消去并整理得,
由韦达定理得,
解得,
则,
因为,,,
所以,,
故.
【解析】由题意,根据题目所给信息以及椭圆和双曲线的性质,列出等式进行求解即可;
结合中信息得到点的坐标,将直线的方程与椭圆方程联立,利用韦达定理求出点的坐标,根据斜率公式再进行求证即可.
本题考查椭圆的性质以及直线与圆锥曲线的综合问题,考查了逻辑推理和运算能力,属于中档题.
第1页,共1页
同课章节目录
