第五章 相交线与平行线 达标检测卷(含解析) 人教版七年级数学下册
文档属性
| 名称 | 第五章 相交线与平行线 达标检测卷(含解析) 人教版七年级数学下册 | 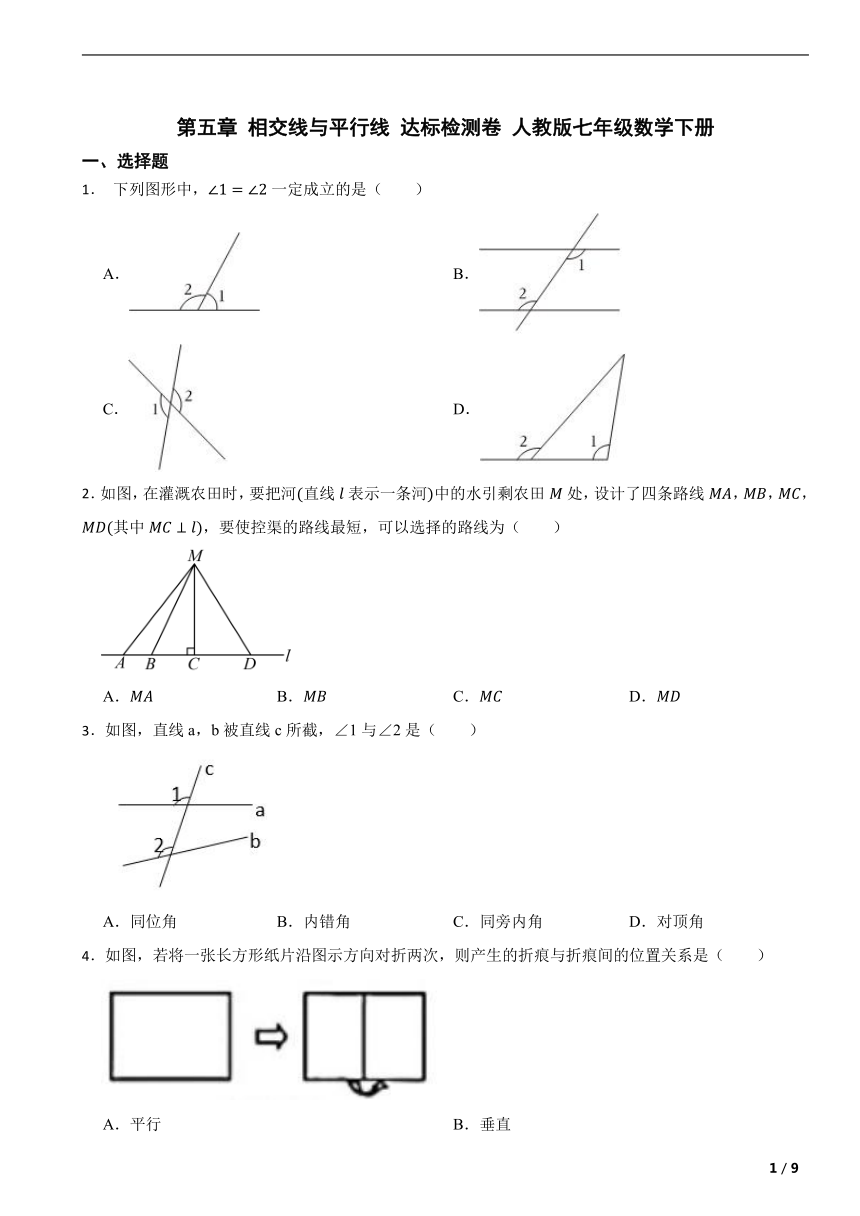 | |
| 格式 | docx | ||
| 文件大小 | 203.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 08:56:28 | ||
图片预览


文档简介
第五章 相交线与平行线 达标检测卷 人教版七年级数学下册
一、选择题
1. 下列图形中,一定成立的是( )
A. B.
C. D.
2.如图,在灌溉农田时,要把河直线表示一条河中的水引剩农田处,设计了四条路线,,,其中,要使控渠的路线最短,可以选择的路线为( )
A. B. C. D.
3.如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
4.如图,若将一张长方形纸片沿图示方向对折两次,则产生的折痕与折痕间的位置关系是( )
A.平行 B.垂直
C.平行或垂直 D.相交但不垂直
5.如图,直线DE∥FG,三角尺ABC的顶点B,C分别在DE,FG上.若∠BCF=25°,则∠ABE的度数为( )
A.25° B.55° C.65° D.75°
6.如图,直线,被第三条直线所截.由“”,得到“”的依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
7.下列语句,是真命题的是( )
A.对顶角相等 B.同位角相等
C.内错角相等 D.同旁内角互补
8.下列图形中,周长最长的是( )
A. B.
C. D.
二、填空题
9.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
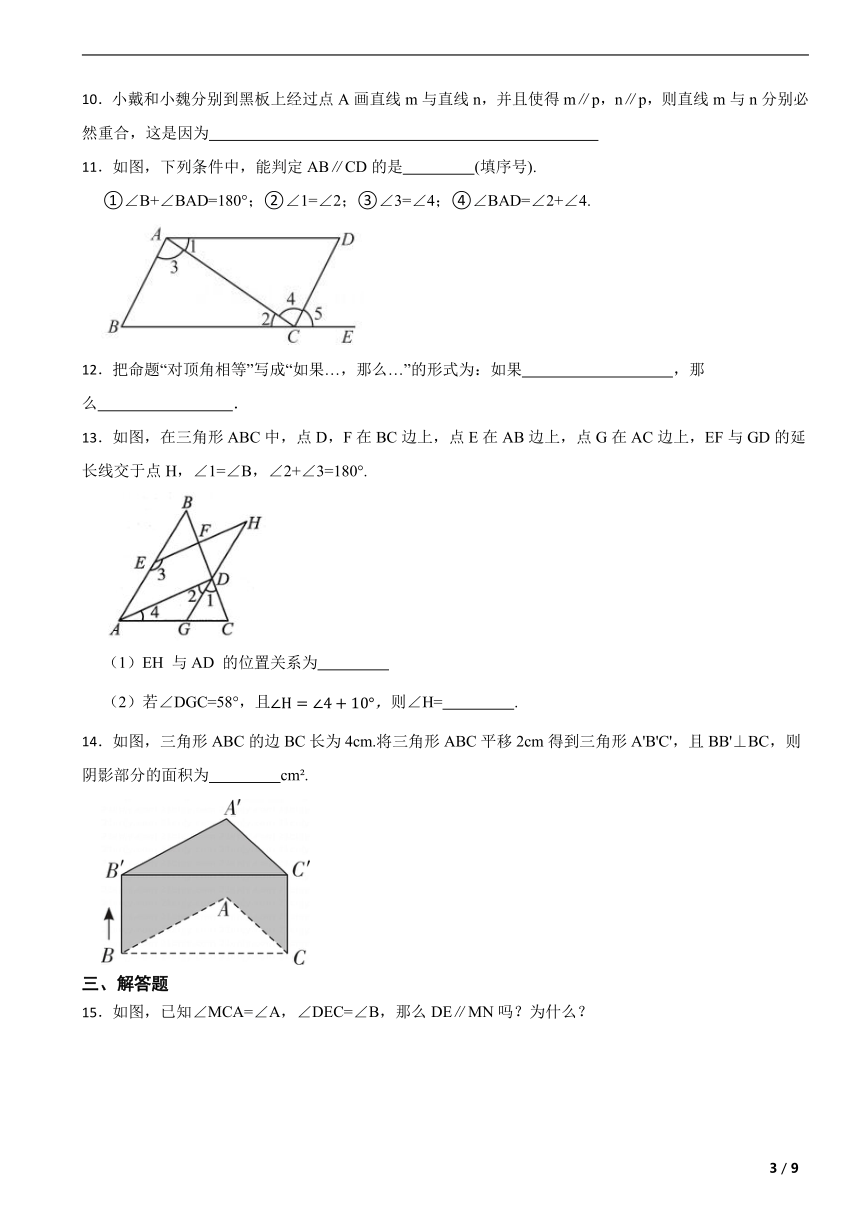
10.小戴和小魏分别到黑板上经过点A画直线m与直线n,并且使得m∥p,n∥p,则直线m与n分别必然重合,这是因为
11.如图,下列条件中,能判定AB∥CD的是 (填序号).
①∠B+∠BAD=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠2+∠4.
12.把命题“对顶角相等”写成“如果…,那么…”的形式为:如果 ,那么 .
13.如图,在三角形ABC中,点D,F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠1=∠B,∠2+∠3=180°.
(1)EH 与AD 的位置关系为
(2)若∠DGC=58°,且则∠H= .
14.如图,三角形ABC的边BC长为4cm.将三角形ABC平移2cm得到三角形A'B'C',且BB'⊥BC,则阴影部分的面积为 cm .
三、解答题
15.如图,已知∠MCA=∠A,∠DEC=∠B,那么DE∥MN吗?为什么?
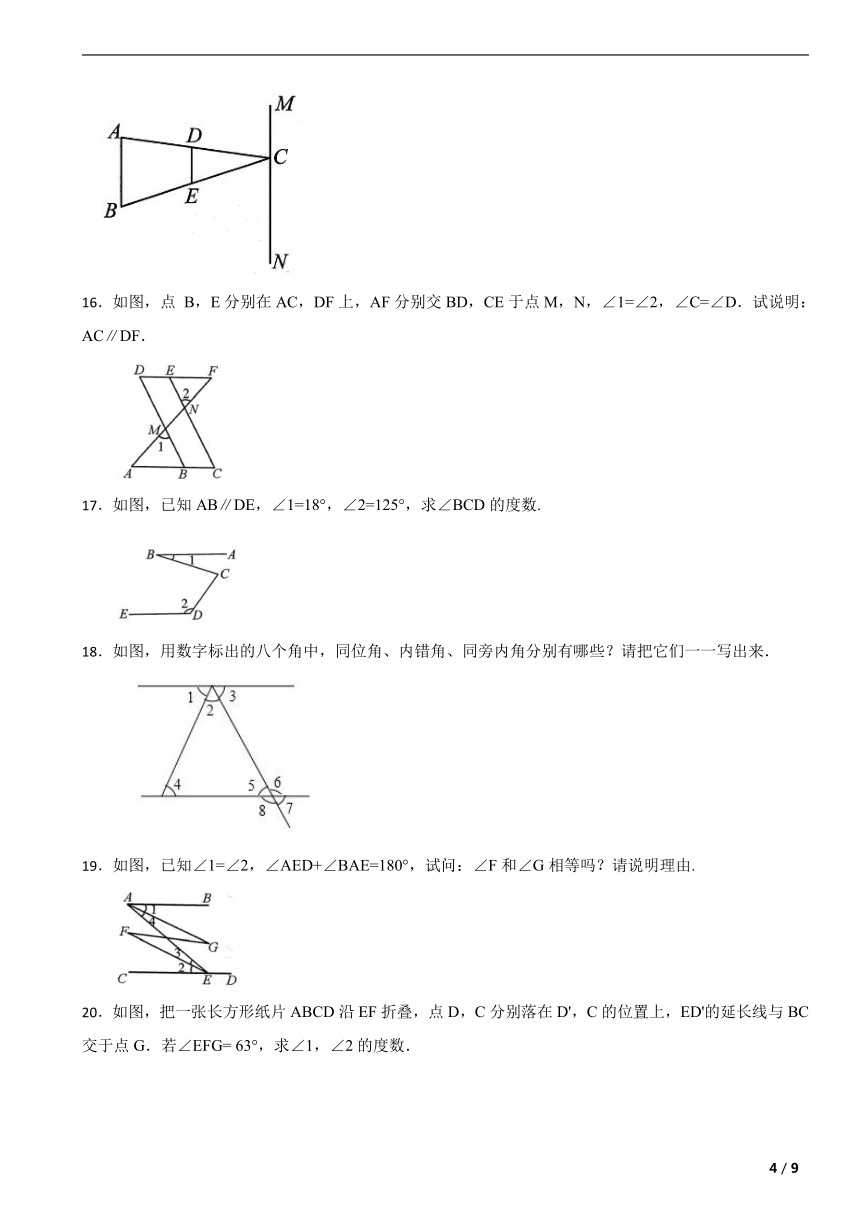
16.如图,点 B,E分别在AC,DF上,AF分别交BD,CE于点M,N,∠1=∠2,∠C=∠D.试说明:AC∥DF.
17.如图,已知AB∥DE,∠1=18°,∠2=125°,求∠BCD的度数.
18.如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.
19.如图,已知∠1=∠2,∠AED+∠BAE=180°,试问:∠F和∠G相等吗?请说明理由.
20.如图,把一张长方形纸片ABCD沿EF折叠,点D,C分别落在D',C的位置上,ED'的延长线与BC交于点G.若∠EFG= 63°,求∠1,∠2的度数.
答案解析部分
1.【答案】C
【解析】【解答】A、根据图形可得,∠1与∠2是补角,但不一定相等,∴A不符合题意;
B、∵两直线平行,内错角相等,但是图中两直线并不一定平行,∴∠1与∠2不一定相等,∴B不符合题意;
C、∵∠1与∠2是对顶角,∴∠1=∠2,∴C符合题意;
D、∵∠2是三角形的外角,∴∠2>∠1,∴D不符合题意;
故答案为:C.
【分析】利用平行线的性质,三角形的外角及对顶角的性质逐项判断即可.
2.【答案】C
【解析】【解答】解:根据“垂线段最短”可知:选择路线MC;
故答案为:C.
【分析】根据“垂线段最短”进行解答即可.
3.【答案】A
【解析】【解答】如图,∠1与∠2两个角都在被截直线a和b的同侧,并且在截线c的同旁,
∴∠1与∠2时同位角.
故答案为:A.
【分析】根据同位角、内错角、同旁内角及对顶角的定义逐一判断即可.
4.【答案】A
5.【答案】C
【解析】【解答】解:
故答案为:C.
【分析】根据两直线平行内错角相等解得∠EBC=25°,再根据角的和差解答即可.
6.【答案】D
【解析】【解答】解:∵∠1=∠2,
∴a∥b(内错角相等,两直线平行),
故答案为:D.
【分析】根据平行线的判定定理:内错角相等,两直线平行。
7.【答案】A
【解析】【解答】A.对顶角相等,所以A选项为真命题;
B.两直线平行,同位角相等,所以B选项为假命题;
C.两直线平行,同错角相等,所以C选项为假命题;
D.两直线平行,同旁内角互补,所以D选项为假命题.
故答案为:A.
【分析】真假命题的判断最简单的方法就是反证法,这也是解题的关键。
8.【答案】A
【解析】【解答】解:A、周长大于12cm,
B、周长为,
C、周长为
D、周长为
故答案为:A.
【分析】通过平移可得,B、C、D选项中图形的周长都等于长是4厘米,宽是2厘米的长方形的周长,A选项中的图形的周长等于长是4厘米,宽是2厘米的长方形的周长加上中间两条竖直线段的长度,所以A选项中的图形的周长最长.
9.【答案】50°
【解析】【解答】解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
【分析】根据两线平行可得到∠A=∠2=∠1,再根据同旁内角可得到答案
10.【答案】过直线外一点,有且只有一条直线与已知直线平行
【解析】【解答】解:∵直线m、n都经过点A,且m∥p,n∥p,
∴ 直线m与n分别必然重合 (过直线外一点,有且只有一条直线与已知直线平行).
故答案为:过直线外一点,有且只有一条直线与已知直线平行.
【分析】根据直线公理:过直线外一点,有且只有一条直线与已知直线平行可得答案.
11.【答案】③
【解析】【解答】解:①、 ,, 故①错误;
②、,, 故②错误;
③ 、,, 故③正确;
④ 、∵,∴∠BAD=∠BCD,由∠BAD=∠BCD判断不出任何直线平行,故④错误.
一定能判定的条件有③.
故答案为:③.
【分析】本题考查了平行线的判定:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行,熟练掌握判定方法是解题关键,根据平行线的判定逐项分析即可.
12.【答案】两个角是对顶角;这两个角相等
【解析】【解答】解:原命题的条件是:“两个角是对顶角”,结论是:“这两个角相等”,
命题“对顶角相等”写成“如果…,那么…”的形式为:“如果两个角是对顶角,那么这两个角相等”.故答案为:两个角是对顶角;这两个角相等.
【分析】先找到命题的题设和结论,再写成“如果…,那么…”的形式.
13.【答案】(1)EH∥AD
(2)34°
14.【答案】8
【解析】【解答】解:∵三角形ABC平移2cm得到三角形A'B'C',
∴
∴阴影部分面积为:S四边形BB'C'C=4×2=8.
故答案为:8.
【分析】根据平移的性质:平移不改变图形的大小,据此即可知阴影部分面积为长方形边形BCC'B'的面积,进而即可求解.
15.【答案】解:DE∥MN。理由如下:∵∠MCA=∠A,∠DEC=∠B,∴AB∥MN,AB∥DE,∴DE∥MN。
16.【答案】解:∵∠1=∠DMF,∠1=∠2,∴∠2=∠DMF,∴BD∥CE,∴∠C=∠DBA.
∵∠C=∠D,∴∠D=∠DBA,∴AC∥DF.
【解析】【解答】
【分析】先利用同位角相等,两直线平行证明BD∥CE,再根据两直线平行,同位角相等得到∠C=∠DBA,等量代换得∠D=∠DBA,根据内错角相等,两直线平行得 AC∥DF .
17.【答案】解:过点C 作CF∥AB,如图所示:∵AB∥DE,CF∥AB,∴CF∥DE,∴∠2+∠4=180°,又∵∠2=125°,∴∠4=55°,又∵CF∥AB,∴∠1=∠3,又∵∠1 变式4答图=18°,∴∠3=18°,又∵∠BCD=∠3+∠4,∴∠BCD =73°.
【解析】【解答】
【分析】过点C作CF∥AB,由平行于同一条直线的两条直线互相平行得到AB∥DE,根据两直线平行,同旁内角互补得∠4=180°- ∠2=55° ;由两直线平行,内错角相等得∠3= ∠1=18° ,∠BCD=∠3+∠4即可求解.
18.【答案】解:内错角:∠1与∠4,∠3与∠5,∠2与∠6,∠4与∠8;
同旁内角:∠3与∠6,∠2与∠5,∠2与∠4,∠4与∠5;
同位角:∠3与∠7,∠2与∠8,∠4与∠6.
【解析】【分析】根据两直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两边,可得内错角,根据两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角的位置相同,可得同位角.
19.【答案】解:相等。理由如下:∵∠AED+∠BAE=180°,∴AB ∥CD,∴∠1+∠4=∠2+∠3.
又∵∠1=∠2,∴∠3=∠4,∴AG∥EF,∴∠F=∠G.
【解析】【解答】
【分析】 ∠AED和∠BAE 是同旁内角,由同旁内角互补,两直线平行得AB ∥CD,再由两直线平行,内错角相等得∠BAE=∠AEC,等量代换得∠3=∠4,根据内错角相等,两直线平行得AG∥EF,最后由两直线平行,内错角相等得∠F=∠G.
20.【答案】解:∵AD∥BC,∴∠DEF=∠EFG=63°,由折叠知∠D'EF=∠DEF=63°,
∴∠1=180°-∠D'EF-∠DEF=54°.∵AD∥BC,∴∠1+∠2=180°,∴∠2=180°-∠1=
【解析】【解答】
【分析】根据两直线平行,内错角相等可得∠DEF=∠EFG=63°,再根据折叠性质可得∠D'EF=∠DEF=63°,即可求得∠1=180°-∠D'EF-∠DEF=54°;两直线平行,同旁内角互补,可得∠1+∠2=180°,即可求出∠2.
1 / 1
一、选择题
1. 下列图形中,一定成立的是( )
A. B.
C. D.
2.如图,在灌溉农田时,要把河直线表示一条河中的水引剩农田处,设计了四条路线,,,其中,要使控渠的路线最短,可以选择的路线为( )
A. B. C. D.
3.如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
4.如图,若将一张长方形纸片沿图示方向对折两次,则产生的折痕与折痕间的位置关系是( )
A.平行 B.垂直
C.平行或垂直 D.相交但不垂直
5.如图,直线DE∥FG,三角尺ABC的顶点B,C分别在DE,FG上.若∠BCF=25°,则∠ABE的度数为( )
A.25° B.55° C.65° D.75°
6.如图,直线,被第三条直线所截.由“”,得到“”的依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
7.下列语句,是真命题的是( )
A.对顶角相等 B.同位角相等
C.内错角相等 D.同旁内角互补
8.下列图形中,周长最长的是( )
A. B.
C. D.
二、填空题
9.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
10.小戴和小魏分别到黑板上经过点A画直线m与直线n,并且使得m∥p,n∥p,则直线m与n分别必然重合,这是因为
11.如图,下列条件中,能判定AB∥CD的是 (填序号).
①∠B+∠BAD=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠2+∠4.
12.把命题“对顶角相等”写成“如果…,那么…”的形式为:如果 ,那么 .
13.如图,在三角形ABC中,点D,F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠1=∠B,∠2+∠3=180°.
(1)EH 与AD 的位置关系为
(2)若∠DGC=58°,且则∠H= .
14.如图,三角形ABC的边BC长为4cm.将三角形ABC平移2cm得到三角形A'B'C',且BB'⊥BC,则阴影部分的面积为 cm .
三、解答题
15.如图,已知∠MCA=∠A,∠DEC=∠B,那么DE∥MN吗?为什么?
16.如图,点 B,E分别在AC,DF上,AF分别交BD,CE于点M,N,∠1=∠2,∠C=∠D.试说明:AC∥DF.
17.如图,已知AB∥DE,∠1=18°,∠2=125°,求∠BCD的度数.
18.如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.
19.如图,已知∠1=∠2,∠AED+∠BAE=180°,试问:∠F和∠G相等吗?请说明理由.
20.如图,把一张长方形纸片ABCD沿EF折叠,点D,C分别落在D',C的位置上,ED'的延长线与BC交于点G.若∠EFG= 63°,求∠1,∠2的度数.
答案解析部分
1.【答案】C
【解析】【解答】A、根据图形可得,∠1与∠2是补角,但不一定相等,∴A不符合题意;
B、∵两直线平行,内错角相等,但是图中两直线并不一定平行,∴∠1与∠2不一定相等,∴B不符合题意;
C、∵∠1与∠2是对顶角,∴∠1=∠2,∴C符合题意;
D、∵∠2是三角形的外角,∴∠2>∠1,∴D不符合题意;
故答案为:C.
【分析】利用平行线的性质,三角形的外角及对顶角的性质逐项判断即可.
2.【答案】C
【解析】【解答】解:根据“垂线段最短”可知:选择路线MC;
故答案为:C.
【分析】根据“垂线段最短”进行解答即可.
3.【答案】A
【解析】【解答】如图,∠1与∠2两个角都在被截直线a和b的同侧,并且在截线c的同旁,
∴∠1与∠2时同位角.
故答案为:A.
【分析】根据同位角、内错角、同旁内角及对顶角的定义逐一判断即可.
4.【答案】A
5.【答案】C
【解析】【解答】解:
故答案为:C.
【分析】根据两直线平行内错角相等解得∠EBC=25°,再根据角的和差解答即可.
6.【答案】D
【解析】【解答】解:∵∠1=∠2,
∴a∥b(内错角相等,两直线平行),
故答案为:D.
【分析】根据平行线的判定定理:内错角相等,两直线平行。
7.【答案】A
【解析】【解答】A.对顶角相等,所以A选项为真命题;
B.两直线平行,同位角相等,所以B选项为假命题;
C.两直线平行,同错角相等,所以C选项为假命题;
D.两直线平行,同旁内角互补,所以D选项为假命题.
故答案为:A.
【分析】真假命题的判断最简单的方法就是反证法,这也是解题的关键。
8.【答案】A
【解析】【解答】解:A、周长大于12cm,
B、周长为,
C、周长为
D、周长为
故答案为:A.
【分析】通过平移可得,B、C、D选项中图形的周长都等于长是4厘米,宽是2厘米的长方形的周长,A选项中的图形的周长等于长是4厘米,宽是2厘米的长方形的周长加上中间两条竖直线段的长度,所以A选项中的图形的周长最长.
9.【答案】50°
【解析】【解答】解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
【分析】根据两线平行可得到∠A=∠2=∠1,再根据同旁内角可得到答案
10.【答案】过直线外一点,有且只有一条直线与已知直线平行
【解析】【解答】解:∵直线m、n都经过点A,且m∥p,n∥p,
∴ 直线m与n分别必然重合 (过直线外一点,有且只有一条直线与已知直线平行).
故答案为:过直线外一点,有且只有一条直线与已知直线平行.
【分析】根据直线公理:过直线外一点,有且只有一条直线与已知直线平行可得答案.
11.【答案】③
【解析】【解答】解:①、 ,, 故①错误;
②、,, 故②错误;
③ 、,, 故③正确;
④ 、∵,∴∠BAD=∠BCD,由∠BAD=∠BCD判断不出任何直线平行,故④错误.
一定能判定的条件有③.
故答案为:③.
【分析】本题考查了平行线的判定:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行,熟练掌握判定方法是解题关键,根据平行线的判定逐项分析即可.
12.【答案】两个角是对顶角;这两个角相等
【解析】【解答】解:原命题的条件是:“两个角是对顶角”,结论是:“这两个角相等”,
命题“对顶角相等”写成“如果…,那么…”的形式为:“如果两个角是对顶角,那么这两个角相等”.故答案为:两个角是对顶角;这两个角相等.
【分析】先找到命题的题设和结论,再写成“如果…,那么…”的形式.
13.【答案】(1)EH∥AD
(2)34°
14.【答案】8
【解析】【解答】解:∵三角形ABC平移2cm得到三角形A'B'C',
∴
∴阴影部分面积为:S四边形BB'C'C=4×2=8.
故答案为:8.
【分析】根据平移的性质:平移不改变图形的大小,据此即可知阴影部分面积为长方形边形BCC'B'的面积,进而即可求解.
15.【答案】解:DE∥MN。理由如下:∵∠MCA=∠A,∠DEC=∠B,∴AB∥MN,AB∥DE,∴DE∥MN。
16.【答案】解:∵∠1=∠DMF,∠1=∠2,∴∠2=∠DMF,∴BD∥CE,∴∠C=∠DBA.
∵∠C=∠D,∴∠D=∠DBA,∴AC∥DF.
【解析】【解答】
【分析】先利用同位角相等,两直线平行证明BD∥CE,再根据两直线平行,同位角相等得到∠C=∠DBA,等量代换得∠D=∠DBA,根据内错角相等,两直线平行得 AC∥DF .
17.【答案】解:过点C 作CF∥AB,如图所示:∵AB∥DE,CF∥AB,∴CF∥DE,∴∠2+∠4=180°,又∵∠2=125°,∴∠4=55°,又∵CF∥AB,∴∠1=∠3,又∵∠1 变式4答图=18°,∴∠3=18°,又∵∠BCD=∠3+∠4,∴∠BCD =73°.
【解析】【解答】
【分析】过点C作CF∥AB,由平行于同一条直线的两条直线互相平行得到AB∥DE,根据两直线平行,同旁内角互补得∠4=180°- ∠2=55° ;由两直线平行,内错角相等得∠3= ∠1=18° ,∠BCD=∠3+∠4即可求解.
18.【答案】解:内错角:∠1与∠4,∠3与∠5,∠2与∠6,∠4与∠8;
同旁内角:∠3与∠6,∠2与∠5,∠2与∠4,∠4与∠5;
同位角:∠3与∠7,∠2与∠8,∠4与∠6.
【解析】【分析】根据两直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两边,可得内错角,根据两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角的位置相同,可得同位角.
19.【答案】解:相等。理由如下:∵∠AED+∠BAE=180°,∴AB ∥CD,∴∠1+∠4=∠2+∠3.
又∵∠1=∠2,∴∠3=∠4,∴AG∥EF,∴∠F=∠G.
【解析】【解答】
【分析】 ∠AED和∠BAE 是同旁内角,由同旁内角互补,两直线平行得AB ∥CD,再由两直线平行,内错角相等得∠BAE=∠AEC,等量代换得∠3=∠4,根据内错角相等,两直线平行得AG∥EF,最后由两直线平行,内错角相等得∠F=∠G.
20.【答案】解:∵AD∥BC,∴∠DEF=∠EFG=63°,由折叠知∠D'EF=∠DEF=63°,
∴∠1=180°-∠D'EF-∠DEF=54°.∵AD∥BC,∴∠1+∠2=180°,∴∠2=180°-∠1=
【解析】【解答】
【分析】根据两直线平行,内错角相等可得∠DEF=∠EFG=63°,再根据折叠性质可得∠D'EF=∠DEF=63°,即可求得∠1=180°-∠D'EF-∠DEF=54°;两直线平行,同旁内角互补,可得∠1+∠2=180°,即可求出∠2.
1 / 1
