2024年中考数学一轮复习考点探究 学案 函数及函数图象的分析与判断(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习考点探究 学案 函数及函数图象的分析与判断(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 304.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:02:22 | ||
图片预览


文档简介
第2节 函数及函数图象的分析与判断
命题分析
在江西学考中,主要考查函数自变量的取值范围、函数图象的性质,2019年考查了以实际问题为背景,结合几何图形探究函数的图象及性质,2022年考查了与化学知识相关的函数图象的分析.
【知识清单】
知识点1 函数及自变量的取值范围
函数及自变量的取值范围
知识点2 函数的表示方法及其图象
1.函数的表示方法
函数的表示方法有三种:解析式法、图象法、列表法.
2.函数图象的概念及画法
(1)函数图象的概念:对于一个函数,如果把自变量x和函数y的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.
(2)用“描点法”作函数图象的三个步骤:
①列表:列表写出一些自变量及其对应的函数值.
②描点:以表中的对应值为坐标,在平面直角坐标系内描出相应的点.
③连线:按自变量从小到大的顺序,把所描的各个点用平滑的曲线顺次连接起来.
(3)判断点是否在函数图象上:把一个点的坐标代入函数解析式,如果等式成立,那么该点在函数图象上;如果等式不成立,那么该点不在函数图象上.
3.函数图象的性质
一般地,函数图象的上升线表示因变量随自变量取值的增大而增大,下降线表示因变量随自变量取值的增大而减小,水平线表示因变量不随自变量取值的变化而发生变化.
【自我诊断】
1.在函数y=中,自变量x的取值范围是 ( )
A.x≤1 B.x≥-1
C.x<-1 D.x>1
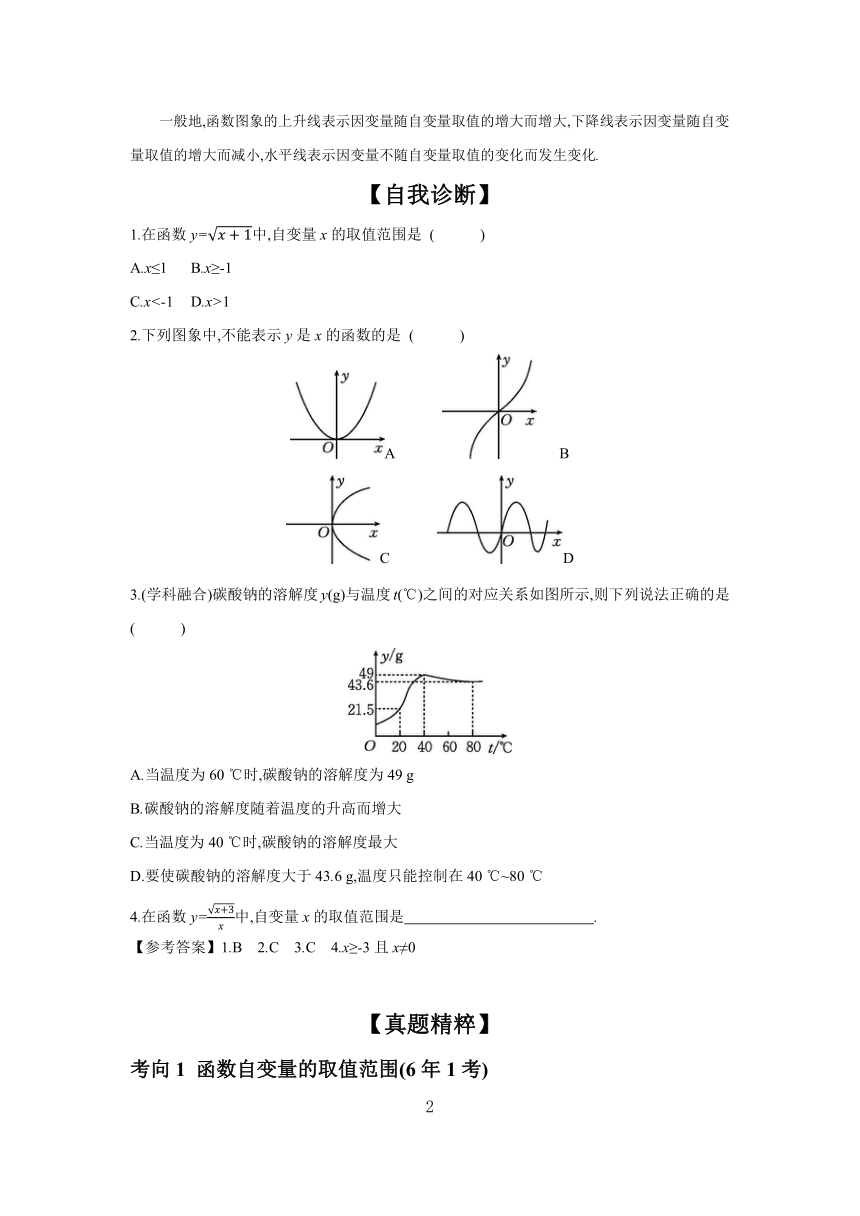
2.下列图象中,不能表示y是x的函数的是 ( )
A B
C D
3.(学科融合)碳酸钠的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法正确的是 ( )
A.当温度为60 ℃时,碳酸钠的溶解度为49 g
B.碳酸钠的溶解度随着温度的升高而增大
C.当温度为40 ℃时,碳酸钠的溶解度最大
D.要使碳酸钠的溶解度大于43.6 g,温度只能控制在40 ℃~80 ℃
4.在函数y=中,自变量x的取值范围是 .
【参考答案】1.B 2.C 3.C 4.x≥-3且x≠0
【真题精粹】
考向1 函数自变量的取值范围(6年1考)
1.(拓展)在函数y=中,自变量x的取值范围是 .
考向2 函数图象的判断(6年1考)
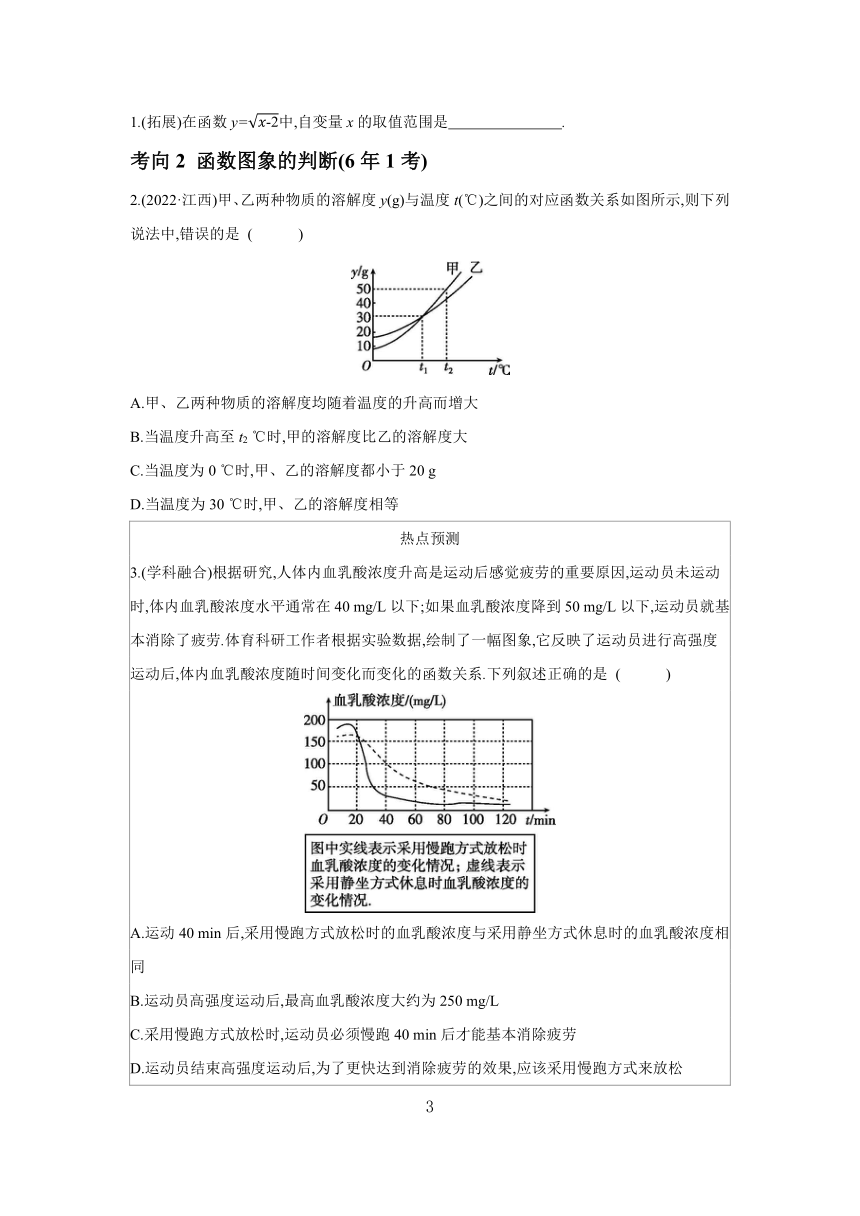
2.(2022·江西)甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应函数关系如图所示,则下列说法中,错误的是 ( )
A.甲、乙两种物质的溶解度均随着温度的升高而增大
B.当温度升高至t2 ℃时,甲的溶解度比乙的溶解度大
C.当温度为0 ℃时,甲、乙的溶解度都小于20 g
D.当温度为30 ℃时,甲、乙的溶解度相等
热点预测
3.(学科融合)根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40 mg/L以下;如果血乳酸浓度降到50 mg/L以下,运动员就基本消除了疲劳.体育科研工作者根据实验数据,绘制了一幅图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是 ( )
A.运动40 min后,采用慢跑方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B.运动员高强度运动后,最高血乳酸浓度大约为250 mg/L
C.采用慢跑方式放松时,运动员必须慢跑40 min后才能基本消除疲劳
D.运动员结束高强度运动后,为了更快达到消除疲劳的效果,应该采用慢跑方式来放松
考向3 函数的三种表达形式(6年1考)
4.(2019·江西)在数学活动课上,张老师引导学生进行如下探究:
如图1,将长为12 cm的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上,一端A固定在桌面上,图2是示意图.
活动一
如图3,将铅笔AB绕端点A顺时针旋转,AB与OF交于点D,当旋转至水平位置时,铅笔AB的中点C与点O重合.
数学思考
(1)设CD=x cm,点B到OF的距离GB=y cm.
①用含x的代数式表示AD的长是 cm,BD的长是 cm.
②y与x之间的函数关系式是 ,自变量x的取值范围是 .
活动二
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
x/cm 6 5 4 3.5 3 2.5 2 1 0.5 0
y/cm 0 0.55 1.2 1.58 2.47 3 4.29 5.08
②描点:根据表中数值,继续描出①中剩余的两个点(x,y).
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请结合函数图象,写出该函数的两条性质或结论.
【参考答案】1.x≥2 2.D 3.D
4.(1)①(6+x);(6-x) ②y=;0≤x≤6
(2)①补全表格如下:
x/cm 6 5 4 3.5 3 2.5 2 1 0.5 0
y/cm 0 0.55 1.2 1.58 2 2.47 3 4.29 5.08 6
②略 ③略 (3)略
【核心突破】
考点1 函数自变量的取值范围
例题1 (2023·宜春模拟)在函数y=中,自变量x的取值范围是 .
变式特训 1.在函数y=中,自变量x的取值范围是 ( )
A.x≥1且x≠3 B.x≥1
C.x≠3 D.x>1且x≠3
考点2 函数图象的判断
例题2在等腰三角形ABC中,AB=CB=5,AC=8,P为AC边上一动点,PQ⊥AC,PQ与△ABC的腰交于点Q,连接CQ.设AP的长为x,△CPQ的面积为y,则y关于x的函数关系的图象大致是 ( )
解题指南
(1)弄清横、纵坐标所表示的量,理清起点和终点.
(2)动点问题找运动过程中的关键点,即对应图象中的拐点,表示函数图象在这一刻开始变化.
变式特训
2.如图,在大烧杯中放了一个小烧杯,现向小烧杯中匀速注水,小烧杯满了后继续匀速注水,则大烧杯的液面高度h(cm)与注水时间t(s)的大致图象是 ( )
A B
C D
3.(2023·南通)已知等腰直角△ABC的斜边AB=4,正方形DEFG的边长为,把△ABC和正方形DEFG按如图所示的方式放置,点B与点E重合,边AB与EF在同一条直线上,将△ABC沿AB方向以每秒 个单位长度的速度匀速平行移动,当点A与点E重合时停止移动.在移动过程中,△ABC与正方形DEFG重叠部分的面积S与移动时间t(s)的函数图象大致是 ( )
A B
C D
考点3 函数的三种表达形式
例题3 已知一个函数的因变量y与自变量x的几组对应值如下表,则这个函数的表达式可以是 ( )
x … -1 0 1 2 …
y … -2 0 2 4 …
A.y=2x B.y=x-1 C.y= D.y=x2
例题4 (学科融合)在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值:
所挂物体质量x/kg 0 1 2 3 4
弹簧长度y/cm 16 18 20 22 24
(1)在这个表格中反映的是 和 两个变量之间的关系; 是自变量, 是因变量.
(2)弹簧长度y(cm)与所挂物体质量x(kg)的关系式是 .
(3)当弹簧的长度为27 cm时,求此时所挂物体的质量.(在弹簧的允许范围内)
例题5小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).
小强根据他学习函数的经验做了如下的探究.下面是小强的探究过程,请补充完整.
(1)建立函数模型:
设矩形小花园的一边长为x米,篱笆长为y米,则y关于x的函数表达式为 .
(2)列表:
根据函数的表达式,得到了几组x与y的对应值,如下表所示,请补全表格.(相关数据保留一位小数)
x 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
y 17.0 10.0 8.3 8.2 8.7 9.3 10.8 11.6
(3)描点、画函数图象:
如图,在平面直角坐标系xOy中,根据表中数值,继续描出(2)中剩余的两个点,并用平滑的曲线画出该函数的图象.
(4)观察分析、得出结论:
根据以上信息,可得当x= 时,y有最小值.由此,小强确定竹篱笆的长至少为 米.
方法提炼
用不同方式表示函数的关键是在“变化过程”中找出自变量与函数值的对应关系.
【参考答案】例题1 x≤3
变式特训
1.A
例题2 C
变式特训
2.D 3.C
例题3 A
例题4 (1)弹簧长度;所挂物体质量;所挂物体质量;弹簧长度
(2)y=16+2x (3)5.5 kg
例题5 (1)y=2x+
(2)表格中从左到右依次填8.0;10.0 (3)略 (4)2;8
2
命题分析
在江西学考中,主要考查函数自变量的取值范围、函数图象的性质,2019年考查了以实际问题为背景,结合几何图形探究函数的图象及性质,2022年考查了与化学知识相关的函数图象的分析.
【知识清单】
知识点1 函数及自变量的取值范围
函数及自变量的取值范围
知识点2 函数的表示方法及其图象
1.函数的表示方法
函数的表示方法有三种:解析式法、图象法、列表法.
2.函数图象的概念及画法
(1)函数图象的概念:对于一个函数,如果把自变量x和函数y的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.
(2)用“描点法”作函数图象的三个步骤:
①列表:列表写出一些自变量及其对应的函数值.
②描点:以表中的对应值为坐标,在平面直角坐标系内描出相应的点.
③连线:按自变量从小到大的顺序,把所描的各个点用平滑的曲线顺次连接起来.
(3)判断点是否在函数图象上:把一个点的坐标代入函数解析式,如果等式成立,那么该点在函数图象上;如果等式不成立,那么该点不在函数图象上.
3.函数图象的性质
一般地,函数图象的上升线表示因变量随自变量取值的增大而增大,下降线表示因变量随自变量取值的增大而减小,水平线表示因变量不随自变量取值的变化而发生变化.
【自我诊断】
1.在函数y=中,自变量x的取值范围是 ( )
A.x≤1 B.x≥-1
C.x<-1 D.x>1
2.下列图象中,不能表示y是x的函数的是 ( )
A B
C D
3.(学科融合)碳酸钠的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法正确的是 ( )
A.当温度为60 ℃时,碳酸钠的溶解度为49 g
B.碳酸钠的溶解度随着温度的升高而增大
C.当温度为40 ℃时,碳酸钠的溶解度最大
D.要使碳酸钠的溶解度大于43.6 g,温度只能控制在40 ℃~80 ℃
4.在函数y=中,自变量x的取值范围是 .
【参考答案】1.B 2.C 3.C 4.x≥-3且x≠0
【真题精粹】
考向1 函数自变量的取值范围(6年1考)
1.(拓展)在函数y=中,自变量x的取值范围是 .
考向2 函数图象的判断(6年1考)
2.(2022·江西)甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应函数关系如图所示,则下列说法中,错误的是 ( )
A.甲、乙两种物质的溶解度均随着温度的升高而增大
B.当温度升高至t2 ℃时,甲的溶解度比乙的溶解度大
C.当温度为0 ℃时,甲、乙的溶解度都小于20 g
D.当温度为30 ℃时,甲、乙的溶解度相等
热点预测
3.(学科融合)根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40 mg/L以下;如果血乳酸浓度降到50 mg/L以下,运动员就基本消除了疲劳.体育科研工作者根据实验数据,绘制了一幅图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是 ( )
A.运动40 min后,采用慢跑方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B.运动员高强度运动后,最高血乳酸浓度大约为250 mg/L
C.采用慢跑方式放松时,运动员必须慢跑40 min后才能基本消除疲劳
D.运动员结束高强度运动后,为了更快达到消除疲劳的效果,应该采用慢跑方式来放松
考向3 函数的三种表达形式(6年1考)
4.(2019·江西)在数学活动课上,张老师引导学生进行如下探究:
如图1,将长为12 cm的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上,一端A固定在桌面上,图2是示意图.
活动一
如图3,将铅笔AB绕端点A顺时针旋转,AB与OF交于点D,当旋转至水平位置时,铅笔AB的中点C与点O重合.
数学思考
(1)设CD=x cm,点B到OF的距离GB=y cm.
①用含x的代数式表示AD的长是 cm,BD的长是 cm.
②y与x之间的函数关系式是 ,自变量x的取值范围是 .
活动二
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
x/cm 6 5 4 3.5 3 2.5 2 1 0.5 0
y/cm 0 0.55 1.2 1.58 2.47 3 4.29 5.08
②描点:根据表中数值,继续描出①中剩余的两个点(x,y).
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请结合函数图象,写出该函数的两条性质或结论.
【参考答案】1.x≥2 2.D 3.D
4.(1)①(6+x);(6-x) ②y=;0≤x≤6
(2)①补全表格如下:
x/cm 6 5 4 3.5 3 2.5 2 1 0.5 0
y/cm 0 0.55 1.2 1.58 2 2.47 3 4.29 5.08 6
②略 ③略 (3)略
【核心突破】
考点1 函数自变量的取值范围
例题1 (2023·宜春模拟)在函数y=中,自变量x的取值范围是 .
变式特训 1.在函数y=中,自变量x的取值范围是 ( )
A.x≥1且x≠3 B.x≥1
C.x≠3 D.x>1且x≠3
考点2 函数图象的判断
例题2在等腰三角形ABC中,AB=CB=5,AC=8,P为AC边上一动点,PQ⊥AC,PQ与△ABC的腰交于点Q,连接CQ.设AP的长为x,△CPQ的面积为y,则y关于x的函数关系的图象大致是 ( )
解题指南
(1)弄清横、纵坐标所表示的量,理清起点和终点.
(2)动点问题找运动过程中的关键点,即对应图象中的拐点,表示函数图象在这一刻开始变化.
变式特训
2.如图,在大烧杯中放了一个小烧杯,现向小烧杯中匀速注水,小烧杯满了后继续匀速注水,则大烧杯的液面高度h(cm)与注水时间t(s)的大致图象是 ( )
A B
C D
3.(2023·南通)已知等腰直角△ABC的斜边AB=4,正方形DEFG的边长为,把△ABC和正方形DEFG按如图所示的方式放置,点B与点E重合,边AB与EF在同一条直线上,将△ABC沿AB方向以每秒 个单位长度的速度匀速平行移动,当点A与点E重合时停止移动.在移动过程中,△ABC与正方形DEFG重叠部分的面积S与移动时间t(s)的函数图象大致是 ( )
A B
C D
考点3 函数的三种表达形式
例题3 已知一个函数的因变量y与自变量x的几组对应值如下表,则这个函数的表达式可以是 ( )
x … -1 0 1 2 …
y … -2 0 2 4 …
A.y=2x B.y=x-1 C.y= D.y=x2
例题4 (学科融合)在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值:
所挂物体质量x/kg 0 1 2 3 4
弹簧长度y/cm 16 18 20 22 24
(1)在这个表格中反映的是 和 两个变量之间的关系; 是自变量, 是因变量.
(2)弹簧长度y(cm)与所挂物体质量x(kg)的关系式是 .
(3)当弹簧的长度为27 cm时,求此时所挂物体的质量.(在弹簧的允许范围内)
例题5小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).
小强根据他学习函数的经验做了如下的探究.下面是小强的探究过程,请补充完整.
(1)建立函数模型:
设矩形小花园的一边长为x米,篱笆长为y米,则y关于x的函数表达式为 .
(2)列表:
根据函数的表达式,得到了几组x与y的对应值,如下表所示,请补全表格.(相关数据保留一位小数)
x 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
y 17.0 10.0 8.3 8.2 8.7 9.3 10.8 11.6
(3)描点、画函数图象:
如图,在平面直角坐标系xOy中,根据表中数值,继续描出(2)中剩余的两个点,并用平滑的曲线画出该函数的图象.
(4)观察分析、得出结论:
根据以上信息,可得当x= 时,y有最小值.由此,小强确定竹篱笆的长至少为 米.
方法提炼
用不同方式表示函数的关键是在“变化过程”中找出自变量与函数值的对应关系.
【参考答案】例题1 x≤3
变式特训
1.A
例题2 C
变式特训
2.D 3.C
例题3 A
例题4 (1)弹簧长度;所挂物体质量;所挂物体质量;弹簧长度
(2)y=16+2x (3)5.5 kg
例题5 (1)y=2x+
(2)表格中从左到右依次填8.0;10.0 (3)略 (4)2;8
2
同课章节目录
