2024年中考数学一轮复习考点探究学案 :三角形的基本概念及性质(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习考点探究学案 :三角形的基本概念及性质(含答案) | 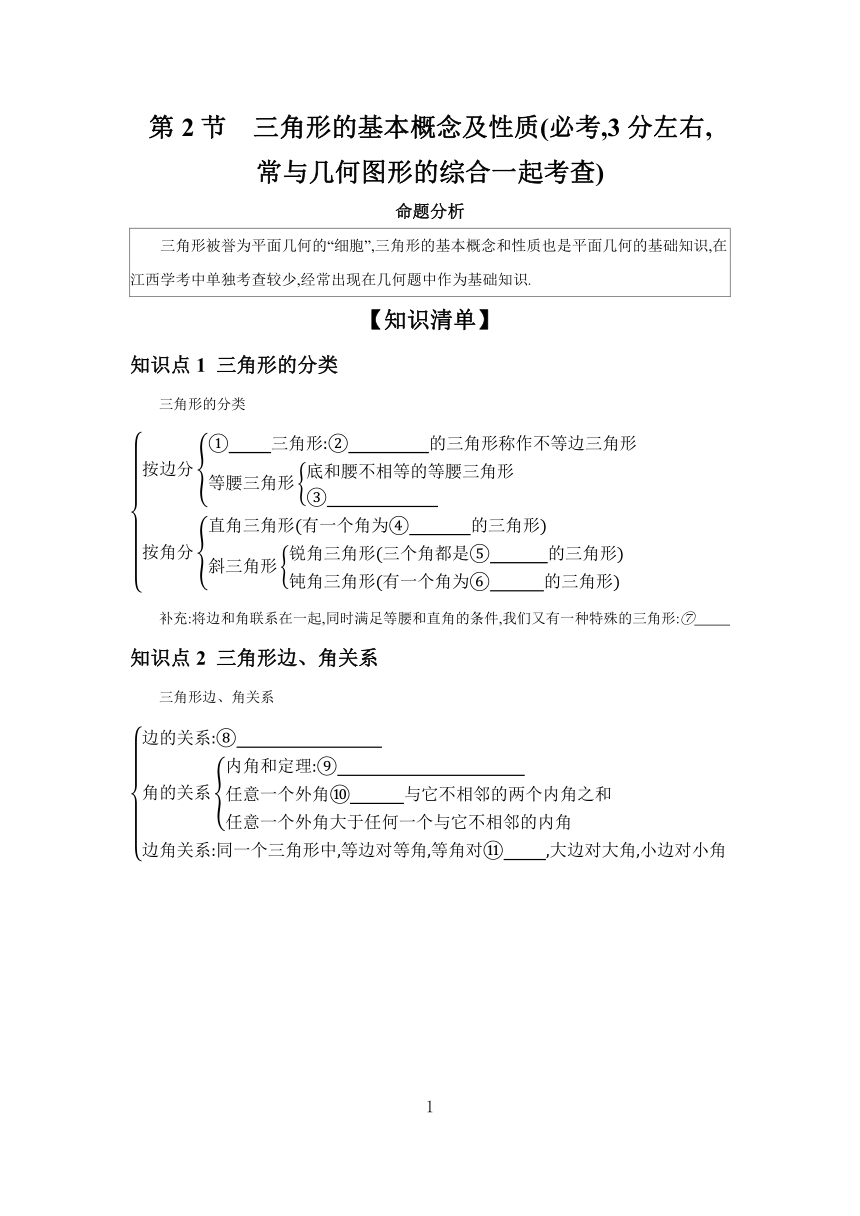 | |
| 格式 | docx | ||
| 文件大小 | 279.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:03:50 | ||
图片预览


文档简介
第2节 三角形的基本概念及性质(必考,3分左右,
常与几何图形的综合一起考查)
命题分析
三角形被誉为平面几何的“细胞”,三角形的基本概念和性质也是平面几何的基础知识,在江西学考中单独考查较少,经常出现在几何题中作为基础知识.
【知识清单】
知识点1 三角形的分类
三角形的分类
补充:将边和角联系在一起,同时满足等腰和直角的条件,我们又有一种特殊的三角形:⑦
知识点2 三角形边、角关系
三角形边、角关系
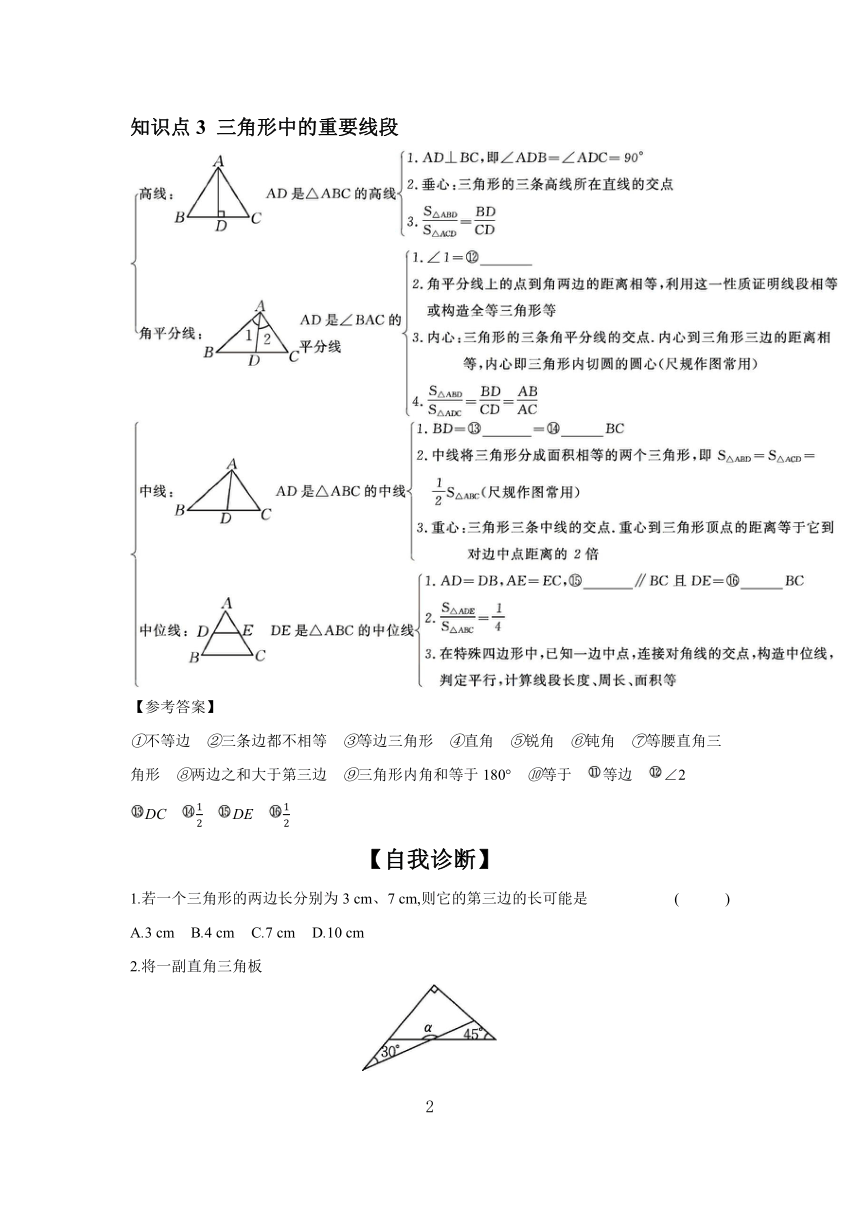
知识点3 三角形中的重要线段
【参考答案】
①不等边 ②三条边都不相等 ③等边三角形 ④直角 ⑤锐角 ⑥钝角 ⑦等腰直角三角形 ⑧两边之和大于第三边 ⑨三角形内角和等于180° ⑩等于 等边 ∠2 DC DE
【自我诊断】
1.若一个三角形的两边长分别为3 cm、7 cm,则它的第三边的长可能是 ( )
A.3 cm B.4 cm C.7 cm D.10 cm
2.将一副直角三角板
按如图所示的方式叠放在一起,则∠α的度数是 ( )
A.165° B.120° C.150° D.135°
3.下列说法正确的是 ( )
A.三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外
B.三角形的角平分线是射线
C.三角形的三条中线交于一点
D.三角形的一条角平分线能把三角形分成两个面积相等的三角形
4.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的 ( )
A.中线
B.中位线
C.高线
D.角平分线
【参考答案】
1.C 2.A 3.C 4.D
【真题精粹】
考向1 三角形边、角的性质(与其他几何图形综合考查)
1.
(拓展)如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为 .
考向2 三角形中的重要线段及其相关计算(与其他几何图形综合考查)
2.
(拓展)如图,在△ABC中,P是△ABC三条角平分线的交点,则∠PBC+∠PCA+∠PAB= 度.
【参考答案】
1.65° 2.90
【核心突破】
考点1 三角形的边、角关系
例题1如图,在△ABC中,D是边BC上的一点,连接AD.
(1)∠BAC+∠B+∠C= .
(2)若∠B=30°,∠BAD=25°,则∠ADC= .
(3)若AB=3,AC=2,则线段BC长的取值范围是 ,∠B ∠C(填“>”、“<”或“=”).
(4)若∠B=30°,AD是BC的垂直平分线,则∠C= .
(5)若∠B=30°,△ABD是等腰三角形,则∠ADB= .
方法提炼
(1)三角形三个内角的和等于180°;(2)三角形的任意一个外角等于与它不相邻的两个内角的和,大于与它不相邻的任意一个内角;(3)三角形三边之间的关系:任意两边之差小于第三边且任意两边之和大于第三边;同一个三角形中,等边对等角,等角对等边,大角对大边(大边对大角);(4)等腰三角形未确定顶角和底角时,要进行分类讨论.
考点2 三角形中的重要线段
例题2在△ABC中,D、E分别为边AC、AB上两点.连接 BD与CE相交于点F.
(1)若BD与CE分别是∠ABC,∠ACB的平分线,则
①点F是△ABC的 心,若∠A=50°,则∠BFC= .
②连接AF,则∠BAF= .
③若点F到AB的距离为2,△ABC的周长为20,则△ABC的面积= .
(2)若BD与CE分别是AC,AB边上的中线,则
①点F是△ABC的 心;S△ABD S△CBD S△ACE S△BCE S△ABC.(填“>”、“<”或“=”)
②若连接AF并延长,交BC于点G,BG=2,则BC= .
③若∠ABC=90°,AC=6,则BD= .
(3)若BD与CE分别是AC,AB边上的高.
①若连接AF并延长交BC于点G,则AG与BC的位置关系为 .
②若∠ABC=62°,∠ACB=50°,则∠BFC= .
③若AB=6,AC=5,CE=4,则BD= .
解题指南
(1)三角形三条角平分线交于一点,交点是三角形的内心;内心到三角形三条边的距离相等,利用等面积公式可以算出△ABC的面积.
(2)三角形三边的中线交于一点,交点为三角形的重心;三角形的中线将三角形分割成两个面积相等的三角形;可通过两条中线确定第三条中线;在直角三角形中,斜边上的中线等于斜边的一半.
(3)三角形三边上的高所在的直线相交于一点,交点是三角形的垂心,可通过两条高线的交点确定第三条高线;利用勾股定理可求出等腰三角形,利用等面积法求出腰上的高.
考点3 与三角形有关的创新作图
例题3如图,在由边长为1的小正方形组成的正方形网格中建立平面直角坐标系,格点△ABC的顶点坐标分别为A(1,6),B(6,6),C(2,2).请仅用无刻度直尺,在给定的网格中依次完成下列作图(要求保留必要的作图痕迹),并回答下列问题:
(1)画出格点A关于直线BC的对称点D,并写出点D的坐标 .
(2)在AB上找到点E,使∠ACE=∠ABC.
(3)作AC边上的高BF.
解题指南
(1)网格作图充分利用正方形的性质得到边角的关系,如∠ABC=45°等.
(2)过点B画AC的垂线,那么我们要找到其中的规律,观察可以发现AC这条线段是横1竖4的长方形的对角线,那么要使得过点B的直线与AC垂直,需要构造出横4竖1的长方形的对角线,连接BP即可达成目的.
【参考答案】
例题1 (1)180° (2)55° (3)1(4)30° (5)30°或120°或75°
例题2 (1)①内 115° ②∠CAF ③20
(2)①重 = = = = ②4 ③3
(3)①AG⊥BC ②112° ③
例题3 (1)略,D(6,1) (2)略 (3)略
2
常与几何图形的综合一起考查)
命题分析
三角形被誉为平面几何的“细胞”,三角形的基本概念和性质也是平面几何的基础知识,在江西学考中单独考查较少,经常出现在几何题中作为基础知识.
【知识清单】
知识点1 三角形的分类
三角形的分类
补充:将边和角联系在一起,同时满足等腰和直角的条件,我们又有一种特殊的三角形:⑦
知识点2 三角形边、角关系
三角形边、角关系
知识点3 三角形中的重要线段
【参考答案】
①不等边 ②三条边都不相等 ③等边三角形 ④直角 ⑤锐角 ⑥钝角 ⑦等腰直角三角形 ⑧两边之和大于第三边 ⑨三角形内角和等于180° ⑩等于 等边 ∠2 DC DE
【自我诊断】
1.若一个三角形的两边长分别为3 cm、7 cm,则它的第三边的长可能是 ( )
A.3 cm B.4 cm C.7 cm D.10 cm
2.将一副直角三角板
按如图所示的方式叠放在一起,则∠α的度数是 ( )
A.165° B.120° C.150° D.135°
3.下列说法正确的是 ( )
A.三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外
B.三角形的角平分线是射线
C.三角形的三条中线交于一点
D.三角形的一条角平分线能把三角形分成两个面积相等的三角形
4.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的 ( )
A.中线
B.中位线
C.高线
D.角平分线
【参考答案】
1.C 2.A 3.C 4.D
【真题精粹】
考向1 三角形边、角的性质(与其他几何图形综合考查)
1.
(拓展)如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为 .
考向2 三角形中的重要线段及其相关计算(与其他几何图形综合考查)
2.
(拓展)如图,在△ABC中,P是△ABC三条角平分线的交点,则∠PBC+∠PCA+∠PAB= 度.
【参考答案】
1.65° 2.90
【核心突破】
考点1 三角形的边、角关系
例题1如图,在△ABC中,D是边BC上的一点,连接AD.
(1)∠BAC+∠B+∠C= .
(2)若∠B=30°,∠BAD=25°,则∠ADC= .
(3)若AB=3,AC=2,则线段BC长的取值范围是 ,∠B ∠C(填“>”、“<”或“=”).
(4)若∠B=30°,AD是BC的垂直平分线,则∠C= .
(5)若∠B=30°,△ABD是等腰三角形,则∠ADB= .
方法提炼
(1)三角形三个内角的和等于180°;(2)三角形的任意一个外角等于与它不相邻的两个内角的和,大于与它不相邻的任意一个内角;(3)三角形三边之间的关系:任意两边之差小于第三边且任意两边之和大于第三边;同一个三角形中,等边对等角,等角对等边,大角对大边(大边对大角);(4)等腰三角形未确定顶角和底角时,要进行分类讨论.
考点2 三角形中的重要线段
例题2在△ABC中,D、E分别为边AC、AB上两点.连接 BD与CE相交于点F.
(1)若BD与CE分别是∠ABC,∠ACB的平分线,则
①点F是△ABC的 心,若∠A=50°,则∠BFC= .
②连接AF,则∠BAF= .
③若点F到AB的距离为2,△ABC的周长为20,则△ABC的面积= .
(2)若BD与CE分别是AC,AB边上的中线,则
①点F是△ABC的 心;S△ABD S△CBD S△ACE S△BCE S△ABC.(填“>”、“<”或“=”)
②若连接AF并延长,交BC于点G,BG=2,则BC= .
③若∠ABC=90°,AC=6,则BD= .
(3)若BD与CE分别是AC,AB边上的高.
①若连接AF并延长交BC于点G,则AG与BC的位置关系为 .
②若∠ABC=62°,∠ACB=50°,则∠BFC= .
③若AB=6,AC=5,CE=4,则BD= .
解题指南
(1)三角形三条角平分线交于一点,交点是三角形的内心;内心到三角形三条边的距离相等,利用等面积公式可以算出△ABC的面积.
(2)三角形三边的中线交于一点,交点为三角形的重心;三角形的中线将三角形分割成两个面积相等的三角形;可通过两条中线确定第三条中线;在直角三角形中,斜边上的中线等于斜边的一半.
(3)三角形三边上的高所在的直线相交于一点,交点是三角形的垂心,可通过两条高线的交点确定第三条高线;利用勾股定理可求出等腰三角形,利用等面积法求出腰上的高.
考点3 与三角形有关的创新作图
例题3如图,在由边长为1的小正方形组成的正方形网格中建立平面直角坐标系,格点△ABC的顶点坐标分别为A(1,6),B(6,6),C(2,2).请仅用无刻度直尺,在给定的网格中依次完成下列作图(要求保留必要的作图痕迹),并回答下列问题:
(1)画出格点A关于直线BC的对称点D,并写出点D的坐标 .
(2)在AB上找到点E,使∠ACE=∠ABC.
(3)作AC边上的高BF.
解题指南
(1)网格作图充分利用正方形的性质得到边角的关系,如∠ABC=45°等.
(2)过点B画AC的垂线,那么我们要找到其中的规律,观察可以发现AC这条线段是横1竖4的长方形的对角线,那么要使得过点B的直线与AC垂直,需要构造出横4竖1的长方形的对角线,连接BP即可达成目的.
【参考答案】
例题1 (1)180° (2)55° (3)1
例题2 (1)①内 115° ②∠CAF ③20
(2)①重 = = = = ②4 ③3
(3)①AG⊥BC ②112° ③
例题3 (1)略,D(6,1) (2)略 (3)略
2
同课章节目录
