2024年江西中考数学一轮复习考点探究 与圆有关的概念及其基本性质 学案(含答案)
文档属性
| 名称 | 2024年江西中考数学一轮复习考点探究 与圆有关的概念及其基本性质 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 277.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:30:00 | ||
图片预览


文档简介
第六章 圆
第1节 与圆有关的概念及其基本性质(6年3考,3~8分)
命题分析
与圆有关的概念及其基本性质是圆的基础知识,江西学考中,一般在圆的综合题中涉及,有时会有1道创新作图题,难度不大.由垂径定理而构成的直角三角形和由直径所对圆周角构成的直角三角形经常考查,圆心角、圆周角定理及推论是圆中进行角的转化的有力工具.另外,隐形圆也是几何压轴题经常涉及的内容之一.
【知识清单】
知识点1 与圆有关的概念及性质
圆的定义 平面上到定点的距离等于定长的所有点的集合,其中定点为① ,定长为②
确定圆的条件 不在同一直线上的三个点确定一个圆
圆的对称性 (1)圆是③ 对称图形,任何一条直径所在的直线都是圆的对称轴;(2)圆是④ 图形,圆心是对称中心
有关概念(如图) 弦 连接圆上任意两点的线段叫做弦(线段AD)
直径 经过圆心的弦叫做直径(线段AB),直径是圆中最长的弦
弦心距 圆心到弦的距离(线段OE的长)
弧 圆上任意两点间的部分叫圆弧:大于半圆的弧叫⑤ (如);小于半圆的弧叫⑥ (如)
等弧 同圆或等圆中,能够互相重合的弧
圆心角 顶点在圆心的角(如∠AOC)
圆周角 顶点在圆上,并且两边都与圆相交的角(如∠ADC)
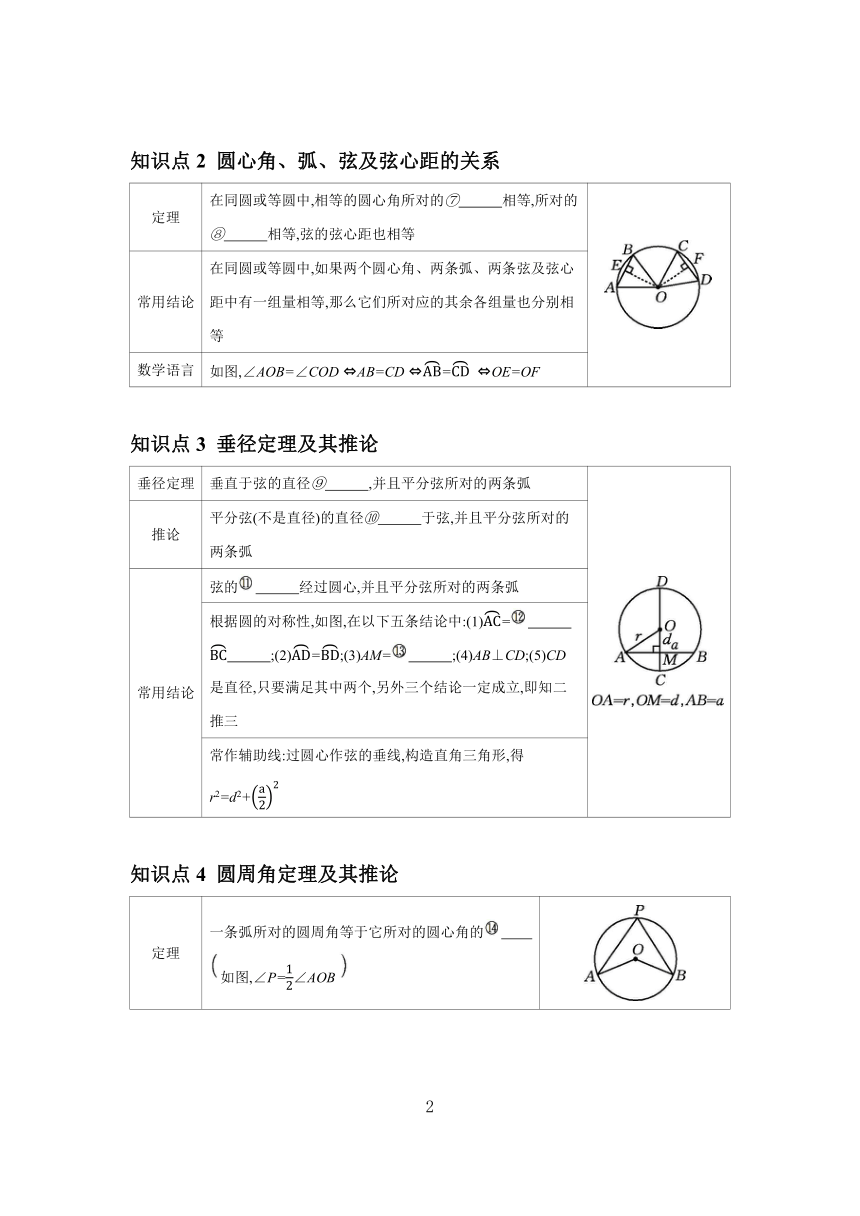
知识点2 圆心角、弧、弦及弦心距的关系
定理 在同圆或等圆中,相等的圆心角所对的⑦ 相等,所对的⑧ 相等,弦的弦心距也相等
常用结论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦及弦心距中有一组量相等,那么它们所对应的其余各组量也分别相等
数学语言 如图,∠AOB=∠COD AB=CD = OE=OF
知识点3 垂径定理及其推论
垂径定理 垂直于弦的直径⑨ ,并且平分弦所对的两条弧
推论 平分弦(不是直径)的直径⑩ 于弦,并且平分弦所对的两条弧
常用结论 弦的 经过圆心,并且平分弦所对的两条弧
根据圆的对称性,如图,在以下五条结论中:(1)= ;(2)=;(3)AM= ;(4)AB⊥CD;(5)CD是直径,只要满足其中两个,另外三个结论一定成立,即知二推三
常作辅助线:过圆心作弦的垂线,构造直角三角形,得r2=d2+
知识点4 圆周角定理及其推论
定理 一条弧所对的圆周角等于它所对的圆心角的 如图,∠P=∠AOB
推论 同弧或等弧所对的圆周角 (如图1,∠A=∠B,∠C=∠D,如图2,∠E=∠F)
半圆(或直径)所对的圆周角是 (如图,∠ACB=90°),90°的圆周角所对的弦是 (如图,∠ACB所对的弦是直径AB)
知识点5 圆的内接多边形温馨提示:圆内接四边形的任意一个外角等于它的内对角(和它相邻的内角的对角).
【参考答案】
①圆心 ②半径 ③轴 ④中心对称 ⑤优弧 ⑥劣弧 ⑦弦 ⑧弧 ⑨平分弦 ⑩垂直 垂直平分线
BM 一半 相等 直角 直径 内接多边形 三角形外接圆的圆心 三个顶点 三边中垂线的交点 不在同一条直线上的三个点 互补
【自我诊断】
1.有下列四种说法:
①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中,错误的说法有 ( )
A.1个 B.2个 C.3个 D.4个
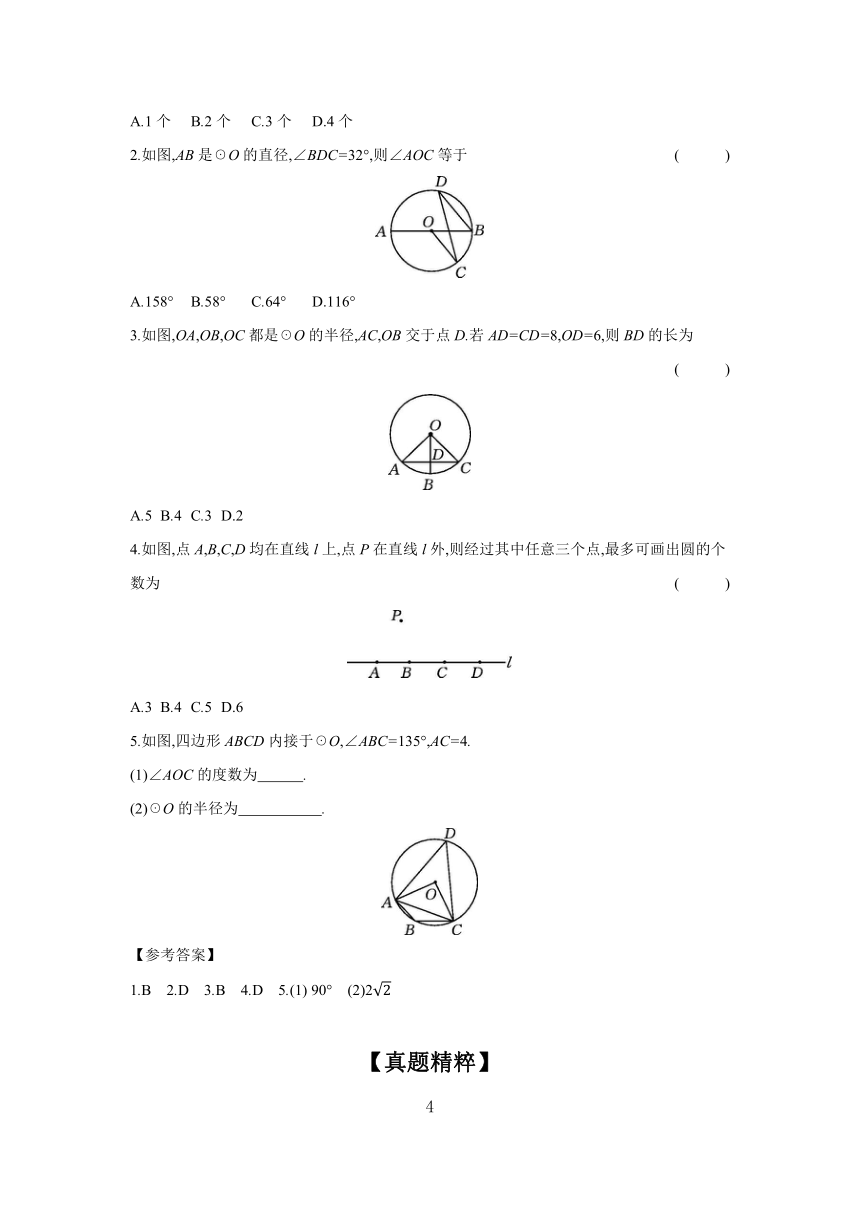
2.如图,AB是☉O的直径,∠BDC=32°,则∠AOC等于 ( )
A.158° B.58° C.64° D.116°
3.如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为 ( )
A.5 B.4 C.3 D.2
4.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为 ( )
A.3 B.4 C.5 D.6
5.如图,四边形ABCD内接于☉O,∠ABC=135°,AC=4.
(1)∠AOC的度数为 .
(2)☉O的半径为 .
【参考答案】
1.B 2.D 3.B 4.D 5.(1) 90° (2)2
【真题精粹】
考向1 垂径定理及其推论
1.(拓展)如图,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8,OF=,则OE的长为 ( )
A.3 B.4 C.2 D.5
考向2 圆周角定理及其推论
2.(拓展)如图,点A,B,C在☉O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为 .
3.(拓展)如图,△ABC内接于☉O,AO=2,BC=2,则∠BAC的度数为 .
【参考答案】
1.A 2.110° 3.60°
【核心突破】
考点1 圆的有关概念与性质
例题1 下列说法正确的是 ( )
A.直径是圆中最长的弦,有4条
B.长度相等的弧是等弧
C.顶点在圆上的角是圆周角
D.弧不一定是半圆,而半圆是弧
变式特训1.若一个圆的半径为5,则该圆的弦长不可能是 ( )
A.1 B.4 C.10 D.11
考点2 弦、弧、圆心角之间的关系
例题2如图,
AB是半圆O的直径,D,C是半圆上的三等分点,则∠ACD的度数是 ( )
A.20° B.30° C.40° D.50°
变式特训2.
如图,C是☉O的直径AB上的一点,过点C作弦DE,使CD=CO.若对应的圆心角的度数为35°,则对应的圆心角的度数是 .
考点3 垂径定理及其推论
例题3
已知AB是☉O中的一条弦,弦AB=8,圆心O到AB的距离为3 cm,则圆的直径为 cm.
变式特训3.AB是☉O的直径,AB垂直于弦CD,垂足为E,若AB=10,CD=8,则线段BE= .
4.(古代科技)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,圆心O在水面上方,且☉O被水面截得的弦AB长为6米,☉O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 ( )
A.1米 B.(4-)米
C.2米 D.(4+)米
考点4 圆周角定理及其推论
例题4
如图,点A,B,C在☉O上,∠ACB=54°,则∠BAO的度数是 ( )
A.54° B.27°
C.36° D.108°
变式特训5.在☉O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角等于 .
考点5 圆的内接四边形
例题5如图,四边形ABCD内接于☉O,D是的中点,若∠B=70°,则∠CAD的度数为 ( )
A.70°
B.55°
C.35°
D.20°
例题6如图,四边形ABCD是☉O的内接四边形,∠B=90°,∠BCD=120°,AB=4,AD=5,则CD的长为
( )
A.2
B.
C.4-
D.3-
变式特训6.如图,四边形ABCD内接于☉O,延长CO交☉O于点E,连接BE.若∠A=100°,∠E=60°,则∠OCD的大小为 .
7.如图,四边形ABCD内接于☉O,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,若CD=10,AF=5,则DF的长为 .
方法提炼
与圆有关的角度及线段计算的解题策略:
1.解决与圆有关角度的相关计算时,一般先判断角是圆周角还是圆心角,再转化成同弧所对的圆周角或圆心角,利用同弧所对圆周角相等,同弧所对圆周角是圆心角的一半关系求解,特别地,当有直径这一条件时,往往要用到直径所对的圆周角是直角这一性质.注意同圆的半径相等这一隐含条件.
2.解决与圆有关线段的相关计算时,通常作弦心距和连接半径构造直角三角形,利用勾股定理,建立方程r2=+(r-h)2来求解.其中r为半径、d为弦长、h为弓高(弧的中点到弦的距离).
【参考答案】
例题1 D
变式特训
1.D
例题2 B
变式特训
2.105°
例题3 10
变式特训
3.2或8
4.B
例题4 C
变式特训
5.60°或120°
例题5 C
例题6 B
变式特训
6.50° 7.5-5
2
第1节 与圆有关的概念及其基本性质(6年3考,3~8分)
命题分析
与圆有关的概念及其基本性质是圆的基础知识,江西学考中,一般在圆的综合题中涉及,有时会有1道创新作图题,难度不大.由垂径定理而构成的直角三角形和由直径所对圆周角构成的直角三角形经常考查,圆心角、圆周角定理及推论是圆中进行角的转化的有力工具.另外,隐形圆也是几何压轴题经常涉及的内容之一.
【知识清单】
知识点1 与圆有关的概念及性质
圆的定义 平面上到定点的距离等于定长的所有点的集合,其中定点为① ,定长为②
确定圆的条件 不在同一直线上的三个点确定一个圆
圆的对称性 (1)圆是③ 对称图形,任何一条直径所在的直线都是圆的对称轴;(2)圆是④ 图形,圆心是对称中心
有关概念(如图) 弦 连接圆上任意两点的线段叫做弦(线段AD)
直径 经过圆心的弦叫做直径(线段AB),直径是圆中最长的弦
弦心距 圆心到弦的距离(线段OE的长)
弧 圆上任意两点间的部分叫圆弧:大于半圆的弧叫⑤ (如);小于半圆的弧叫⑥ (如)
等弧 同圆或等圆中,能够互相重合的弧
圆心角 顶点在圆心的角(如∠AOC)
圆周角 顶点在圆上,并且两边都与圆相交的角(如∠ADC)
知识点2 圆心角、弧、弦及弦心距的关系
定理 在同圆或等圆中,相等的圆心角所对的⑦ 相等,所对的⑧ 相等,弦的弦心距也相等
常用结论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦及弦心距中有一组量相等,那么它们所对应的其余各组量也分别相等
数学语言 如图,∠AOB=∠COD AB=CD = OE=OF
知识点3 垂径定理及其推论
垂径定理 垂直于弦的直径⑨ ,并且平分弦所对的两条弧
推论 平分弦(不是直径)的直径⑩ 于弦,并且平分弦所对的两条弧
常用结论 弦的 经过圆心,并且平分弦所对的两条弧
根据圆的对称性,如图,在以下五条结论中:(1)= ;(2)=;(3)AM= ;(4)AB⊥CD;(5)CD是直径,只要满足其中两个,另外三个结论一定成立,即知二推三
常作辅助线:过圆心作弦的垂线,构造直角三角形,得r2=d2+
知识点4 圆周角定理及其推论
定理 一条弧所对的圆周角等于它所对的圆心角的 如图,∠P=∠AOB
推论 同弧或等弧所对的圆周角 (如图1,∠A=∠B,∠C=∠D,如图2,∠E=∠F)
半圆(或直径)所对的圆周角是 (如图,∠ACB=90°),90°的圆周角所对的弦是 (如图,∠ACB所对的弦是直径AB)
知识点5 圆的内接多边形温馨提示:圆内接四边形的任意一个外角等于它的内对角(和它相邻的内角的对角).
【参考答案】
①圆心 ②半径 ③轴 ④中心对称 ⑤优弧 ⑥劣弧 ⑦弦 ⑧弧 ⑨平分弦 ⑩垂直 垂直平分线
BM 一半 相等 直角 直径 内接多边形 三角形外接圆的圆心 三个顶点 三边中垂线的交点 不在同一条直线上的三个点 互补
【自我诊断】
1.有下列四种说法:
①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中,错误的说法有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图,AB是☉O的直径,∠BDC=32°,则∠AOC等于 ( )
A.158° B.58° C.64° D.116°
3.如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为 ( )
A.5 B.4 C.3 D.2
4.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为 ( )
A.3 B.4 C.5 D.6
5.如图,四边形ABCD内接于☉O,∠ABC=135°,AC=4.
(1)∠AOC的度数为 .
(2)☉O的半径为 .
【参考答案】
1.B 2.D 3.B 4.D 5.(1) 90° (2)2
【真题精粹】
考向1 垂径定理及其推论
1.(拓展)如图,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8,OF=,则OE的长为 ( )
A.3 B.4 C.2 D.5
考向2 圆周角定理及其推论
2.(拓展)如图,点A,B,C在☉O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为 .
3.(拓展)如图,△ABC内接于☉O,AO=2,BC=2,则∠BAC的度数为 .
【参考答案】
1.A 2.110° 3.60°
【核心突破】
考点1 圆的有关概念与性质
例题1 下列说法正确的是 ( )
A.直径是圆中最长的弦,有4条
B.长度相等的弧是等弧
C.顶点在圆上的角是圆周角
D.弧不一定是半圆,而半圆是弧
变式特训1.若一个圆的半径为5,则该圆的弦长不可能是 ( )
A.1 B.4 C.10 D.11
考点2 弦、弧、圆心角之间的关系
例题2如图,
AB是半圆O的直径,D,C是半圆上的三等分点,则∠ACD的度数是 ( )
A.20° B.30° C.40° D.50°
变式特训2.
如图,C是☉O的直径AB上的一点,过点C作弦DE,使CD=CO.若对应的圆心角的度数为35°,则对应的圆心角的度数是 .
考点3 垂径定理及其推论
例题3
已知AB是☉O中的一条弦,弦AB=8,圆心O到AB的距离为3 cm,则圆的直径为 cm.
变式特训3.AB是☉O的直径,AB垂直于弦CD,垂足为E,若AB=10,CD=8,则线段BE= .
4.(古代科技)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,圆心O在水面上方,且☉O被水面截得的弦AB长为6米,☉O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 ( )
A.1米 B.(4-)米
C.2米 D.(4+)米
考点4 圆周角定理及其推论
例题4
如图,点A,B,C在☉O上,∠ACB=54°,则∠BAO的度数是 ( )
A.54° B.27°
C.36° D.108°
变式特训5.在☉O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角等于 .
考点5 圆的内接四边形
例题5如图,四边形ABCD内接于☉O,D是的中点,若∠B=70°,则∠CAD的度数为 ( )
A.70°
B.55°
C.35°
D.20°
例题6如图,四边形ABCD是☉O的内接四边形,∠B=90°,∠BCD=120°,AB=4,AD=5,则CD的长为
( )
A.2
B.
C.4-
D.3-
变式特训6.如图,四边形ABCD内接于☉O,延长CO交☉O于点E,连接BE.若∠A=100°,∠E=60°,则∠OCD的大小为 .
7.如图,四边形ABCD内接于☉O,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,若CD=10,AF=5,则DF的长为 .
方法提炼
与圆有关的角度及线段计算的解题策略:
1.解决与圆有关角度的相关计算时,一般先判断角是圆周角还是圆心角,再转化成同弧所对的圆周角或圆心角,利用同弧所对圆周角相等,同弧所对圆周角是圆心角的一半关系求解,特别地,当有直径这一条件时,往往要用到直径所对的圆周角是直角这一性质.注意同圆的半径相等这一隐含条件.
2.解决与圆有关线段的相关计算时,通常作弦心距和连接半径构造直角三角形,利用勾股定理,建立方程r2=+(r-h)2来求解.其中r为半径、d为弦长、h为弓高(弧的中点到弦的距离).
【参考答案】
例题1 D
变式特训
1.D
例题2 B
变式特训
2.105°
例题3 10
变式特训
3.2或8
4.B
例题4 C
变式特训
5.60°或120°
例题5 C
例题6 B
变式特训
6.50° 7.5-5
2
同课章节目录
