2024年江西中考数学一轮复习考点探究 与圆有关的位置关系 学案 (含答案)
文档属性
| 名称 | 2024年江西中考数学一轮复习考点探究 与圆有关的位置关系 学案 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 279.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:30:53 | ||
图片预览



文档简介
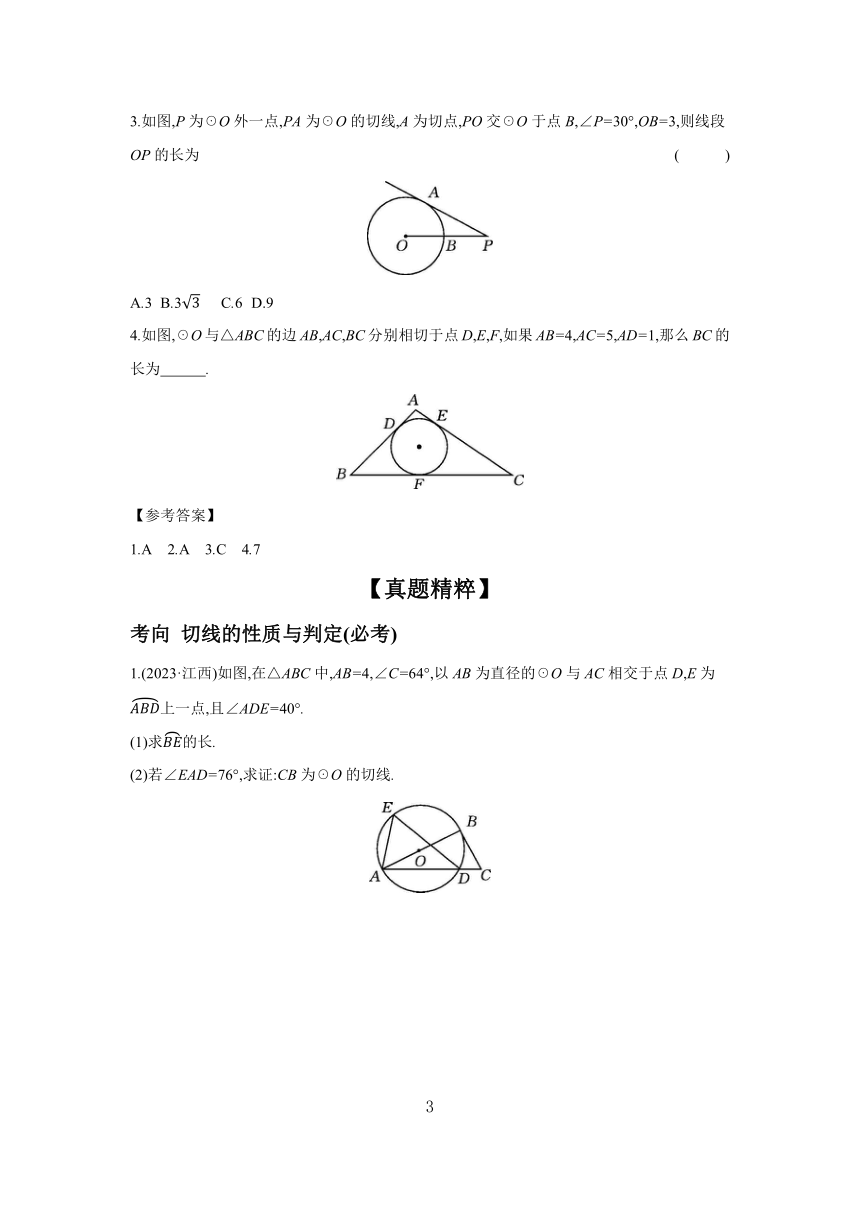
第2节 与圆有关的位置关系(必考,6~9分)
命题分析
圆的切线的性质与判定是江西学考的必考内容,圆的综合题中基本都会涉及,往往需要用到勾股定理、锐角三角函数等知识求解,与圆的切线相关的画图题也会考查,难度适中.
【知识清单】
知识点1 与圆有关的位置关系
图1
点与圆的位置关系
(设圆的半径为r,
平面内任一点到
圆心的距离为d)
直线与圆的位置关系(设圆的半径为r,圆心到直线的距离为d)
知识点2 切线
切线的性质:圆的切线⑦ 于过切点的半径(或直径)
切线的判定
图2
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长⑧ ,这一点和圆心的连线⑨ 两条切线的夹角,如图2,过☉O外一点P可引两条切线PA,PB,则PA=⑩ ,PO平分∠APB
知识点3 三角形的内心
【参考答案】
①> ②= ③< ④> ⑤= ⑥< ⑦垂直 ⑧相等
⑨平分 ⑩PB 与三角形各边相切的圆 三角形内切圆的圆心 各边 三条角平分线
【自我诊断】
1.已知☉O的半径为3,OA=5,则点A在 ( )
A.在☉O外 B.在☉O上
C.在☉O内 D.无法确定
2.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆 ( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
3.如图,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段OP的长为 ( )
A.3 B.3 C.6 D.9
4.如图,☉O与△ABC的边AB,AC,BC分别相切于点D,E,F,如果AB=4,AC=5,AD=1,那么BC的长为 .
【参考答案】
1.A 2.A 3.C 4.7
【真题精粹】
考向 切线的性质与判定(必考)
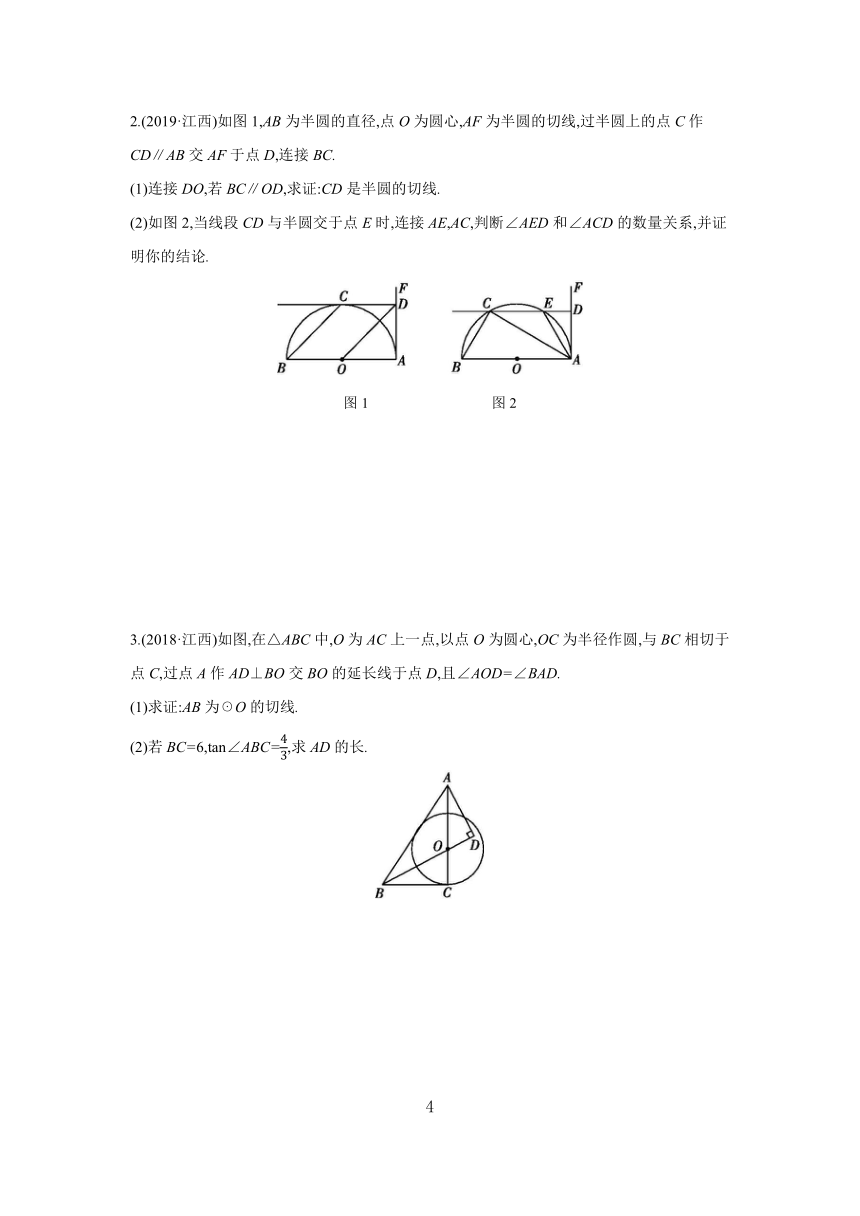
1.(2023·江西)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的☉O与AC相交于点D,E为上一点,且∠ADE=40°.
(1)求的长.
(2)若∠EAD=76°,求证:CB为☉O的切线.
2.(2019·江西)如图1,AB为半圆的直径,点O为圆心,AF为半圆的切线,过半圆上的点C作CD∥AB交AF于点D,连接BC.
(1)连接DO,若BC∥OD,求证:CD是半圆的切线.
(2)如图2,当线段CD与半圆交于点E时,连接AE,AC,判断∠AED和∠ACD的数量关系,并证明你的结论.
图1 图2
3.(2018·江西)如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点C,过点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD.
(1)求证:AB为☉O的切线.
(2)若BC=6,tan∠ABC=,求AD的长.
热点预测
4.如图,AB为☉O的直径,D为☉O上一点,BC⊥CD于点C,交☉O于点E,CD与BA的延长线交于点F,BD平分∠ABC.
(1)求证:CD是☉O的切线.
(2)若AB=10,CE=1,求DF的长.
【参考答案】
1.(1) (2)略
2.(1)略 (2)∠AED+∠ACD=90°.证明略
3.(1)略 (2)2 4.(1)略 (2)
【核心突破】
考点1 点与圆的位置关系
例题1 已知☉O的半径为8 cm.
(1)在同一个平面内,若点P到圆心O的距离为5 cm,则点P在☉O .(填“内”、“上”或“外”)
(2)如图,若P是☉O外一点,且PO=12 cm,Q是☉O上的一个动点,则PQ的最小值是 ,PQ的最大值是 .
解题指南
本题考查平面内点与圆的位置关系和最值问题.
(1)当点与圆心的距离dr时,点在圆的外部.
(2)当P,Q,O三点共线时,PQ存在最值.最小值为PO-r=12-8=4 cm,最大值为PO+r=12+8=20 cm.
变式特训1.P是非圆上一点,若点P到☉O上的点的最小距离是4 cm,最大距离是10 cm,则☉O的半径是 .
考点2 线与圆的位置关系
例题2如图,在Rt△ACB中,∠C=90°,BC=3,AC=4.
(1)以C为圆心,3为半径的☉C与直线AB的位置关系是 .
(2)以点B为圆心,3为半径的☉B与直线AC的位置关系是 .
(3)以点A为圆心,3为半径的☉A与直线BC的位置关系是 .
方法提炼
圆心到直线的距离记为d,当dr时,直线与圆的位置关系为相离.
例题3如图,在☉O中,点O为圆心,半径为5,AB为圆上的一条弦,且AB=8,C为☉O上一动点,过点C作CD⊥AB于点D.
(1)如图1,当点C在劣弧 上时,求CD的最大值及△ABC面积的最大值.
(2)如图2,当点C在优弧 上时,求CD的最大值及△ABC面积的最大值.
考点3 切线的性质与判定
例题4如图,AB为☉O的直径,C为☉O上一点,过点C作☉O的切线交AB的延长线于点D,DB=AD,连接AC,若AB=4,则AC的长为 ( )
A.2
B.
C.4
D.2
变式特训2.如图,PA,PB分别与☉O相切于A,B两点,C为☉O上一点,连接AC,BC,
若∠P=80°,则∠ACB的度数为 ( )
A.80° B.40° C.50° D.70°
3.如图,在△ABC中,以AB为直径作☉O交AC,BC于点D,E,且D是AC的中点,过点D作DG⊥BC于点G,交BA的延长线于点H.
(1)求证:直线HG是☉O的切线.
(2)若HA=3,cos B=,求CG的长.
4.如图,在△ABC中,∠BAC=90°,过点A,B的☉O分别交AC,BC于点D,E,AB=AE,CD的垂直平分线交BC于点F,连接DF.
(1)求证:DF是☉O的切线.
(2)已知EF=3,DE=4,求BE和AB的长.
方法提炼
与圆切线相关的综合问题的解题方法:
1.判断一条直线是否为圆的切线的方法:①知道直线和圆有公共点时,连半径,证垂直;②不知道直线和圆有无公共点时,作垂直,证明垂线段等于半径.
2.利用切线的性质解决问题时,通常连过切点的半径,利用直角三角形的性质来解决问题.
3.直角三角形的外接圆与内切圆半径的求法:若a,b是Rt△ABC的两条直角边,c为斜边,则①外接圆半径R=;②内切圆半径r=.
4.对于涉及圆切线性质与判定的综合问题,往往涉及全等、相似等知识点,能综合运用进行推理是解题的关键.
考点4 切线长定理
例题5 如图,
从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长为 ( )
A.8 B.4 C.4 D.8
变式特训5.如图,
这是用一把直尺、含60°角的直角三角板和光盘摆放而成的图形,A为60°角与直尺的交点,B为光盘与直尺唯一的交点,若AB=3,则光盘的直径是 ( )
A.6 B.3 C.6 D.3
考点5 三角形的内心和外心
例题6
如图,在正方形ABCD中,E是对角线BD上一点(不与点B重合),若点O是△BEC的内心,则∠COE ( )
A.大小为定值,等于112.5°
B.大小不确定,可以等于90°
C.大小为定值,等于127.5°
D.大小不确定,随着点E的变化而变化
变式特训 6.如图,在正方形网格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心 ( )
A.△ACE B.△ABD
C.△ACD D.△BCE
7. 如图,在Rt△ABC中,内切圆O的半径为r,☉O与△ABC各边分别相切于点D,E和F,已知AD=3,BD=2,则r的值为 .
【参考答案】
例题1 (1) 内 (2) 4 cm 20 cm
变式特训
1.7 cm或3 cm
例题2 (1)相交 (2)相切 (3)相离
例题3 (1)CD=2,△ABC面积的最大值=8
(2)CD=8,△ABC面积的最大值=32
例题4 D
变式特训
2.C
3.(1)略 (2) 4.(1)略 (2)BE=,AB=
例题5 A
变式特训
5.A
例题6 A
变式特训
6.D 7.1
2
命题分析
圆的切线的性质与判定是江西学考的必考内容,圆的综合题中基本都会涉及,往往需要用到勾股定理、锐角三角函数等知识求解,与圆的切线相关的画图题也会考查,难度适中.
【知识清单】
知识点1 与圆有关的位置关系
图1
点与圆的位置关系
(设圆的半径为r,
平面内任一点到
圆心的距离为d)
直线与圆的位置关系(设圆的半径为r,圆心到直线的距离为d)
知识点2 切线
切线的性质:圆的切线⑦ 于过切点的半径(或直径)
切线的判定
图2
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长⑧ ,这一点和圆心的连线⑨ 两条切线的夹角,如图2,过☉O外一点P可引两条切线PA,PB,则PA=⑩ ,PO平分∠APB
知识点3 三角形的内心
【参考答案】
①> ②= ③< ④> ⑤= ⑥< ⑦垂直 ⑧相等
⑨平分 ⑩PB 与三角形各边相切的圆 三角形内切圆的圆心 各边 三条角平分线
【自我诊断】
1.已知☉O的半径为3,OA=5,则点A在 ( )
A.在☉O外 B.在☉O上
C.在☉O内 D.无法确定
2.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆 ( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
3.如图,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段OP的长为 ( )
A.3 B.3 C.6 D.9
4.如图,☉O与△ABC的边AB,AC,BC分别相切于点D,E,F,如果AB=4,AC=5,AD=1,那么BC的长为 .
【参考答案】
1.A 2.A 3.C 4.7
【真题精粹】
考向 切线的性质与判定(必考)
1.(2023·江西)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的☉O与AC相交于点D,E为上一点,且∠ADE=40°.
(1)求的长.
(2)若∠EAD=76°,求证:CB为☉O的切线.
2.(2019·江西)如图1,AB为半圆的直径,点O为圆心,AF为半圆的切线,过半圆上的点C作CD∥AB交AF于点D,连接BC.
(1)连接DO,若BC∥OD,求证:CD是半圆的切线.
(2)如图2,当线段CD与半圆交于点E时,连接AE,AC,判断∠AED和∠ACD的数量关系,并证明你的结论.
图1 图2
3.(2018·江西)如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点C,过点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD.
(1)求证:AB为☉O的切线.
(2)若BC=6,tan∠ABC=,求AD的长.
热点预测
4.如图,AB为☉O的直径,D为☉O上一点,BC⊥CD于点C,交☉O于点E,CD与BA的延长线交于点F,BD平分∠ABC.
(1)求证:CD是☉O的切线.
(2)若AB=10,CE=1,求DF的长.
【参考答案】
1.(1) (2)略
2.(1)略 (2)∠AED+∠ACD=90°.证明略
3.(1)略 (2)2 4.(1)略 (2)
【核心突破】
考点1 点与圆的位置关系
例题1 已知☉O的半径为8 cm.
(1)在同一个平面内,若点P到圆心O的距离为5 cm,则点P在☉O .(填“内”、“上”或“外”)
(2)如图,若P是☉O外一点,且PO=12 cm,Q是☉O上的一个动点,则PQ的最小值是 ,PQ的最大值是 .
解题指南
本题考查平面内点与圆的位置关系和最值问题.
(1)当点与圆心的距离d
(2)当P,Q,O三点共线时,PQ存在最值.最小值为PO-r=12-8=4 cm,最大值为PO+r=12+8=20 cm.
变式特训1.P是非圆上一点,若点P到☉O上的点的最小距离是4 cm,最大距离是10 cm,则☉O的半径是 .
考点2 线与圆的位置关系
例题2如图,在Rt△ACB中,∠C=90°,BC=3,AC=4.
(1)以C为圆心,3为半径的☉C与直线AB的位置关系是 .
(2)以点B为圆心,3为半径的☉B与直线AC的位置关系是 .
(3)以点A为圆心,3为半径的☉A与直线BC的位置关系是 .
方法提炼
圆心到直线的距离记为d,当d
例题3如图,在☉O中,点O为圆心,半径为5,AB为圆上的一条弦,且AB=8,C为☉O上一动点,过点C作CD⊥AB于点D.
(1)如图1,当点C在劣弧 上时,求CD的最大值及△ABC面积的最大值.
(2)如图2,当点C在优弧 上时,求CD的最大值及△ABC面积的最大值.
考点3 切线的性质与判定
例题4如图,AB为☉O的直径,C为☉O上一点,过点C作☉O的切线交AB的延长线于点D,DB=AD,连接AC,若AB=4,则AC的长为 ( )
A.2
B.
C.4
D.2
变式特训2.如图,PA,PB分别与☉O相切于A,B两点,C为☉O上一点,连接AC,BC,
若∠P=80°,则∠ACB的度数为 ( )
A.80° B.40° C.50° D.70°
3.如图,在△ABC中,以AB为直径作☉O交AC,BC于点D,E,且D是AC的中点,过点D作DG⊥BC于点G,交BA的延长线于点H.
(1)求证:直线HG是☉O的切线.
(2)若HA=3,cos B=,求CG的长.
4.如图,在△ABC中,∠BAC=90°,过点A,B的☉O分别交AC,BC于点D,E,AB=AE,CD的垂直平分线交BC于点F,连接DF.
(1)求证:DF是☉O的切线.
(2)已知EF=3,DE=4,求BE和AB的长.
方法提炼
与圆切线相关的综合问题的解题方法:
1.判断一条直线是否为圆的切线的方法:①知道直线和圆有公共点时,连半径,证垂直;②不知道直线和圆有无公共点时,作垂直,证明垂线段等于半径.
2.利用切线的性质解决问题时,通常连过切点的半径,利用直角三角形的性质来解决问题.
3.直角三角形的外接圆与内切圆半径的求法:若a,b是Rt△ABC的两条直角边,c为斜边,则①外接圆半径R=;②内切圆半径r=.
4.对于涉及圆切线性质与判定的综合问题,往往涉及全等、相似等知识点,能综合运用进行推理是解题的关键.
考点4 切线长定理
例题5 如图,
从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长为 ( )
A.8 B.4 C.4 D.8
变式特训5.如图,
这是用一把直尺、含60°角的直角三角板和光盘摆放而成的图形,A为60°角与直尺的交点,B为光盘与直尺唯一的交点,若AB=3,则光盘的直径是 ( )
A.6 B.3 C.6 D.3
考点5 三角形的内心和外心
例题6
如图,在正方形ABCD中,E是对角线BD上一点(不与点B重合),若点O是△BEC的内心,则∠COE ( )
A.大小为定值,等于112.5°
B.大小不确定,可以等于90°
C.大小为定值,等于127.5°
D.大小不确定,随着点E的变化而变化
变式特训 6.如图,在正方形网格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心 ( )
A.△ACE B.△ABD
C.△ACD D.△BCE
7. 如图,在Rt△ABC中,内切圆O的半径为r,☉O与△ABC各边分别相切于点D,E和F,已知AD=3,BD=2,则r的值为 .
【参考答案】
例题1 (1) 内 (2) 4 cm 20 cm
变式特训
1.7 cm或3 cm
例题2 (1)相交 (2)相切 (3)相离
例题3 (1)CD=2,△ABC面积的最大值=8
(2)CD=8,△ABC面积的最大值=32
例题4 D
变式特训
2.C
3.(1)略 (2) 4.(1)略 (2)BE=,AB=
例题5 A
变式特训
5.A
例题6 A
变式特训
6.D 7.1
2
同课章节目录
