2024年江西中考数学一轮复习考点探究 投影、视图与尺规作图 学案(含答案)
文档属性
| 名称 | 2024年江西中考数学一轮复习考点探究 投影、视图与尺规作图 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 754.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:34:22 | ||
图片预览



文档简介
第七章 图形的变化
第1节 投影、视图与尺规作图
命题分析
投影、视图与仅用无刻度直尺作图(创新作图)是必考内容,在江西学考中常有1道视图题和1道作图题(1道选择题和1道解答题).在江西学考中常考查简单组合体的三视图,几何体的展开图,仅用无刻度直尺的作图题近几年必考,也是江西学考的特色题型之一.
【知识清单】
知识点1 尺规作图
五种基本尺规作图 步骤 图示 作图痕迹原理 适用情形
作一条线段等于已知线段(已知线段a) 1.作射线OP; 2.以点O为圆心,a为半径作弧,交OP于点A,则OA即所求线段 圆上的点到圆心的距离等于半径 1.已知三边作三角形; 2.作圆的内接正六边形
作一个角等于已知角(已知∠α) 1.以点O为圆心,适当长为半径作弧,分别交∠α的两边于点P,Q; 2.作射线O'A; 3.以点O'为圆心,OP长为半径作弧,交O'A于点M; 4.以① 为圆心;② 为半径作弧,交步骤3中的弧于点N; 5.过点N作射线O'B,则∠AO'B即所求角 1.三边相等的两个三角形全等; 2.全等三角形的对应角相等 1.过直线外一点作直线与已知直线平行; 2.过三角形一边上一点作直线,将其分成两个相似三角形
作已知角的平分线(已知∠AOB) 1.以点O为圆心,适当长为半径作弧,分别交OA,OB于点N,M; 2.分别以③ 为圆心,以④ 为半径作弧,两弧在∠AOB的内部相交于点P; 3.作射线OP,则OP即已知角的平分线 1.三边相等的两个三角形全等; 2.全等三角形的对应角相等; 3.两点确定一条直线 1.作一点使得该点到角两边的距离相等; 2.作三角形的内切圆
(续表)
五种基本尺规作图 步骤 图示 作图痕迹原理 适用情形
作线段的垂直平分线(已知线段AB) 1.分别以⑤ 为圆心,以⑥ 为半径,在AB两侧作弧,分别交于点M,N; 2.过点M,N作直线,直线MN即所求垂直平分线 1.到线段两端点距离相等的点在这条线段的垂直平分线上; 2.两点确定一条直线的外接圆 1.过三角形的一个顶点作直线平分三角形的面积; 2.过不在同一直线上的三点作圆/作三角形的外接圆; 3.作到已知两点距离相等的点
过一点 作已知 直线的 垂线(已 知点P和 直线l) 点P在 直线l上 1.以点P为圆心,适当长为半径作弧,交直线 于A,B两点; 2.分别以⑦ 为圆心,以⑧ 为半径向直线两侧作弧,两弧分别交于点M,N; 3.过点M,N作直线,直线MN即所求垂线 1.到线段两端点距离相等的点在这条线段的垂直平分线上; 2.两点确定一条直线 1.已知底边上的高线及腰长作等腰三角形; 2.过直线外一点作与该直线相切的圆
点P在 直线l外 1.任意取一点M,使点M和点P在直线l的两侧; 2.以⑨ 为圆心, 为半径作弧,交直线l于A,B两点; 3.分别以 为圆心,以 为半径作弧,交点M同侧于点N; 4.过点P,N作直线,直线PN即所求垂线
知识点2 投影与视图
投影
三视图
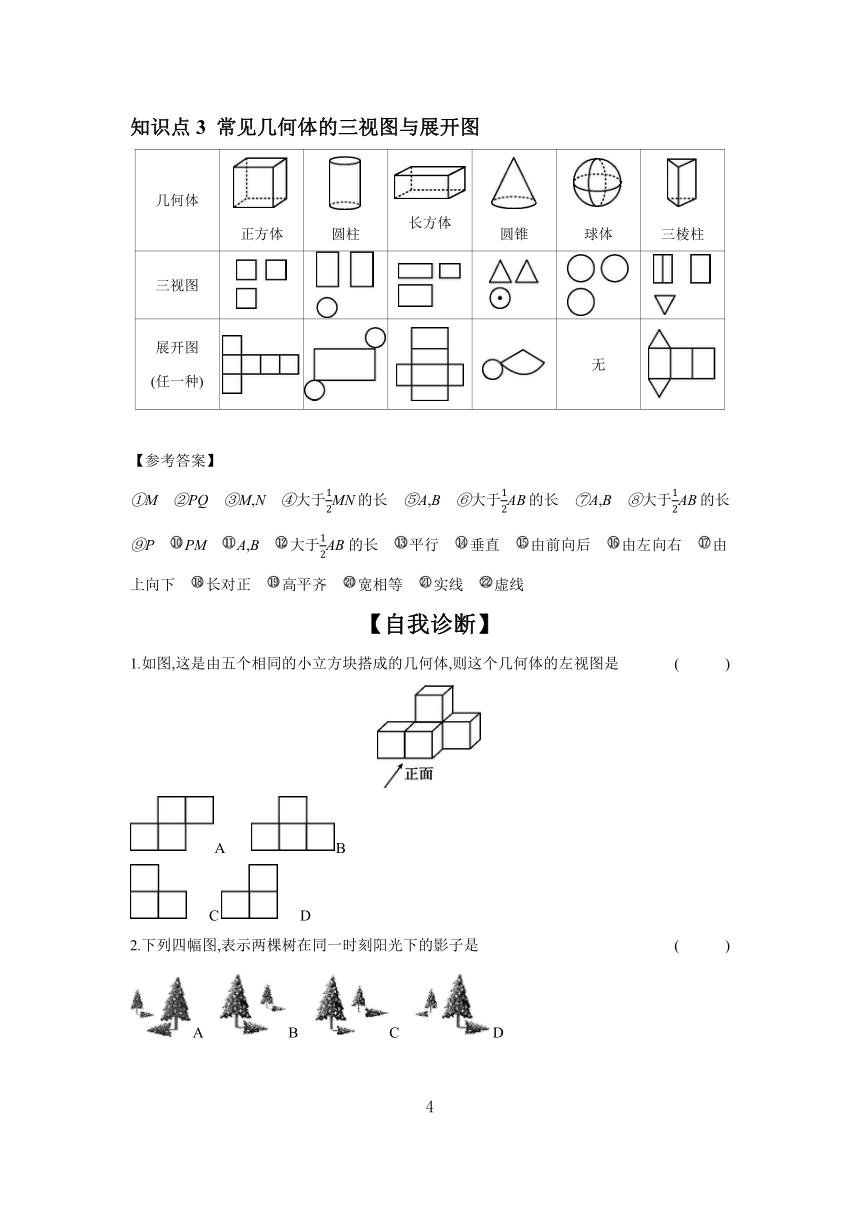
知识点3 常见几何体的三视图与展开图
几何体 正方体 圆柱 长方体 圆锥 球体 三棱柱
三视图
展开图 (任一种) 无
【参考答案】
①M ②PQ ③M,N ④大于MN的长 ⑤A,B ⑥大于AB的长 ⑦A,B ⑧大于AB的长 ⑨P PM A,B 大于AB的长 平行 垂直 由前向后 由左向右 由上向下 长对正 高平齐 宽相等 实线 虚线
【自我诊断】
1.如图,这是由五个相同的小立方块搭成的几何体,则这个几何体的左视图是 ( )
A B
C D
2.下列四幅图,表示两棵树在同一时刻阳光下的影子是 ( )
A B C D
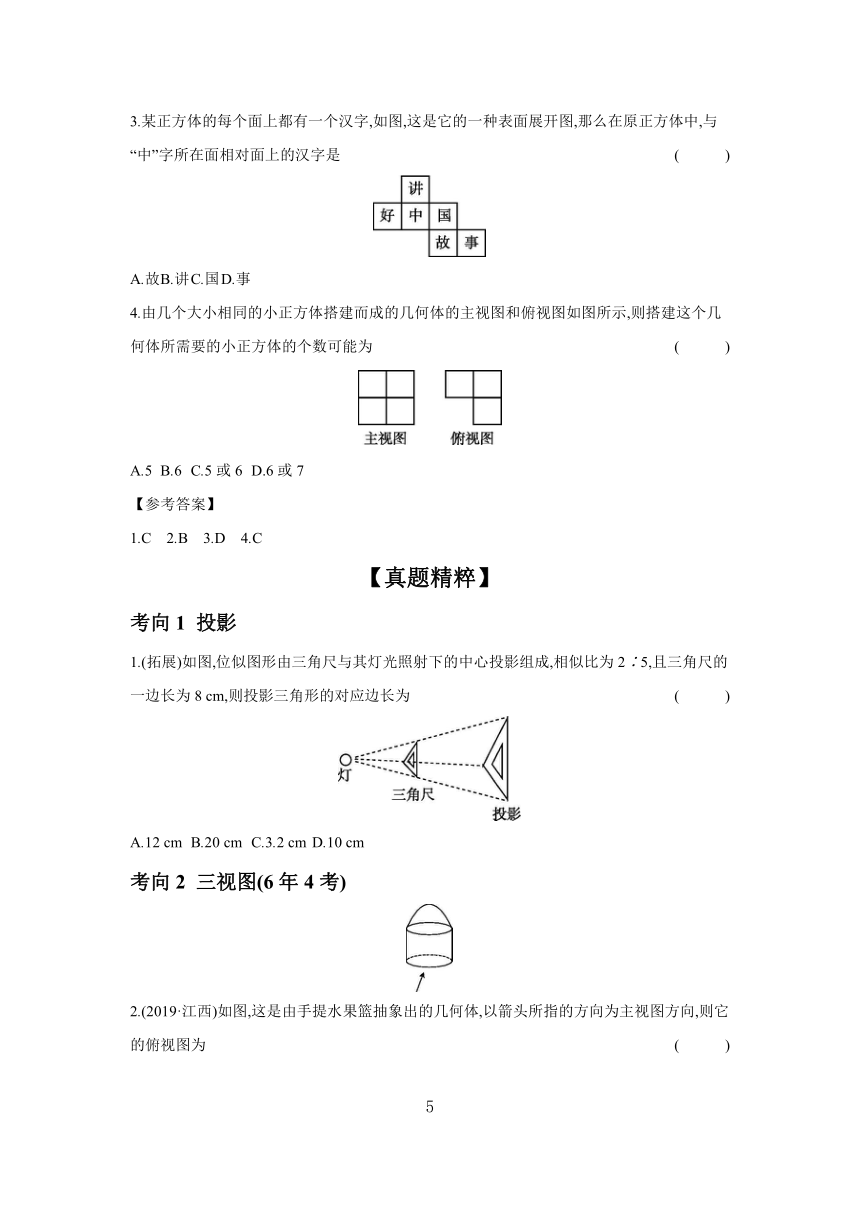
3.某正方体的每个面上都有一个汉字,如图,这是它的一种表面展开图,那么在原正方体中,与“中”字所在面相对面上的汉字是 ( )
A.故 B.讲 C.国 D.事
4.由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图如图所示,则搭建这个几何体所需要的小正方体的个数可能为 ( )
A.5 B.6 C.5或6 D.6或7
【参考答案】
1.C 2.B 3.D 4.C
【真题精粹】
考向1 投影
1.(拓展)如图,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为 ( )
A.12 cm B.20 cm C.3.2 cm D.10 cm
考向2 三视图(6年4考)
2.(2019·江西)如图,这是由手提水果篮抽象出的几何体,以箭头所指的方向为主视图方向,则它的俯视图为 ( )
A B C D
3.(2021·江西)如图所示的几何体的主视图是 ( )
A B C D
4.(2018·江西)如图所示的几何体的左视图为 ( )
5.(2022·江西)如图,这是由四个完全相同的小正方体搭成的几何体,它的俯视图为 ( )
A B C D
热点预测
6.(劳动实践)某学校组织学生到工厂劳动实践,学习制作机械零件的基本流程,如图,这是一种“工”型液压机的配件,它的俯视图是 ( )
A B C D
考向3 创新作图(必考)
7.(2023·江西)如图,这是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)在图1中作锐角△ABC,使点C在格点上.
(2)在图2中的线段AB上作点Q,使PQ最短.
8.(2018·江西)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度直尺分别按下列要求画图.(保留画图痕迹)
(1)在图1中,画出△ABD中BD边上的中线.
(2)在图2中,若BA=BD,画出△ABD中AD边上的高.
图1 图2
9.(2021·江西)已知正方形ABCD的边长为4个单位长度,E是CD的中点,请仅用无刻度直尺按下列要求作图.(保留作图痕迹)
(1)在图1中,将直线AC绕着正方形ABCD的中心顺时针旋转45°.
(2)在图2中,将直线AC向上平移1个单位长度.
热点预测
10.如图,在5×3的正方形网格中,每个小格的顶点叫作格点,点A,B,C均在格点上,按下列要求画图.
(1)在图1中,画出一个 ABCD,使顶点D在格点上.
(2)在图2中,画出一条线段BE,使BE⊥AC,且点E在格点上.
考向4 立体图形的展开图与折叠(仅2020年考查)
11.(2020·江西)如图,正方体的展开图为 ( )
【参考答案】
1.B 2.A 3.C 4.D 5.A 6.D
7.略 8.略 9.略 10.略 11.A
【核心突破】
考点1 投影
例题1 如图,树AB在路灯O的照射下形成投影AC,若树高AB=2 m,树影AC=3 m,树与路灯的水平距离AP=4.5 m,则路灯的高度OP是 ( )
A.3 m B.4 m C.5 m D.6 m
变式特训1.如图1,随着光伏发电项目投资成本下降,越来越多的“光伏”项目正在逐步走进我们的生活.光伏发电不仅能为城市提供清洁能源,还能减少城市污染和能源消耗.如图2,长BC=8 m,宽AB=1.5 m的太阳能电池板与水平面成30°夹角,经过太阳光的正投影,它在水平面所形成的阴影的面积为 ( )
A.12 m2 B.6 m2
C.6 m2 D. m2
考点2 三视图
例题2(2023·鹰潭模拟) 如图,该几何体的左视图是 ( )
A B C D
变式特训2.(民族文化)江西茶文化源远流长,其历史可追溯到两千年前的秦汉时期.如图,这是江西名茶中一种装茶的罐子及抽象出的立体图形,则其主视图为 ( )
A B C D
3.(古人智慧)在我国古代建筑中经常使用榫卯构件,如图,这是某种榫卯构件的示意图,其中卯的俯视图是 ( )
A B
C D
考点3 立体图形的展开与折叠
例题3(2023·巴中)某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是 ( )
A.传 B.承
C.文 D.化
方法提炼
变式特训4.一个骰子相对两面的点数之和为7,它的展开图如图所示,下列判断正确的是 ( )
A.A代表 B.B代表
C.C代表 D.B代表
5.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则下列序号中不应剪去的是 ( )
A.3 B.2 C.6 D.1
6.三棱柱的展开图不可能是 ( )
A B
C D
考点4 创新作图
例题4 (2023·鹰潭模拟) 图1,图2都是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.请仅用无刻度直尺在网格中完成下列画图.
(1)在图1中,画出△ABC中AB边上的中线CM.
(2)在图2中,画出∠APC,使∠APC=∠ABC,且点P在格点上.(画出一个即可)
变式特训7.已知四边形ABCD为平行四边形,E为AB边的中点,请仅用无刻度直尺分别按下列要求作图.(保留作图痕迹)
(1)在图1中,作出AD边的中点P.
(2)在图2中,在AD边上求作一点M,使△ABM的面积为 ABCD面积的.
8.在图1,图2中,四边形ABCD为矩形,某圆经过A,B两点,请你仅用无刻度直尺分别按下列要求作图.
(1)在图1中画出该圆的圆心O.
(2)在图2中画出线段CD的垂直平分线.
【参考答案】
例题1 C
变式特训
1.C
例题2 B
变式特训
2.D 3.C
例题3 D
变式特训
4.A 5.A 6.D
例题4 略
变式特训
7.略 8.略
2
第1节 投影、视图与尺规作图
命题分析
投影、视图与仅用无刻度直尺作图(创新作图)是必考内容,在江西学考中常有1道视图题和1道作图题(1道选择题和1道解答题).在江西学考中常考查简单组合体的三视图,几何体的展开图,仅用无刻度直尺的作图题近几年必考,也是江西学考的特色题型之一.
【知识清单】
知识点1 尺规作图
五种基本尺规作图 步骤 图示 作图痕迹原理 适用情形
作一条线段等于已知线段(已知线段a) 1.作射线OP; 2.以点O为圆心,a为半径作弧,交OP于点A,则OA即所求线段 圆上的点到圆心的距离等于半径 1.已知三边作三角形; 2.作圆的内接正六边形
作一个角等于已知角(已知∠α) 1.以点O为圆心,适当长为半径作弧,分别交∠α的两边于点P,Q; 2.作射线O'A; 3.以点O'为圆心,OP长为半径作弧,交O'A于点M; 4.以① 为圆心;② 为半径作弧,交步骤3中的弧于点N; 5.过点N作射线O'B,则∠AO'B即所求角 1.三边相等的两个三角形全等; 2.全等三角形的对应角相等 1.过直线外一点作直线与已知直线平行; 2.过三角形一边上一点作直线,将其分成两个相似三角形
作已知角的平分线(已知∠AOB) 1.以点O为圆心,适当长为半径作弧,分别交OA,OB于点N,M; 2.分别以③ 为圆心,以④ 为半径作弧,两弧在∠AOB的内部相交于点P; 3.作射线OP,则OP即已知角的平分线 1.三边相等的两个三角形全等; 2.全等三角形的对应角相等; 3.两点确定一条直线 1.作一点使得该点到角两边的距离相等; 2.作三角形的内切圆
(续表)
五种基本尺规作图 步骤 图示 作图痕迹原理 适用情形
作线段的垂直平分线(已知线段AB) 1.分别以⑤ 为圆心,以⑥ 为半径,在AB两侧作弧,分别交于点M,N; 2.过点M,N作直线,直线MN即所求垂直平分线 1.到线段两端点距离相等的点在这条线段的垂直平分线上; 2.两点确定一条直线的外接圆 1.过三角形的一个顶点作直线平分三角形的面积; 2.过不在同一直线上的三点作圆/作三角形的外接圆; 3.作到已知两点距离相等的点
过一点 作已知 直线的 垂线(已 知点P和 直线l) 点P在 直线l上 1.以点P为圆心,适当长为半径作弧,交直线 于A,B两点; 2.分别以⑦ 为圆心,以⑧ 为半径向直线两侧作弧,两弧分别交于点M,N; 3.过点M,N作直线,直线MN即所求垂线 1.到线段两端点距离相等的点在这条线段的垂直平分线上; 2.两点确定一条直线 1.已知底边上的高线及腰长作等腰三角形; 2.过直线外一点作与该直线相切的圆
点P在 直线l外 1.任意取一点M,使点M和点P在直线l的两侧; 2.以⑨ 为圆心, 为半径作弧,交直线l于A,B两点; 3.分别以 为圆心,以 为半径作弧,交点M同侧于点N; 4.过点P,N作直线,直线PN即所求垂线
知识点2 投影与视图
投影
三视图
知识点3 常见几何体的三视图与展开图
几何体 正方体 圆柱 长方体 圆锥 球体 三棱柱
三视图
展开图 (任一种) 无
【参考答案】
①M ②PQ ③M,N ④大于MN的长 ⑤A,B ⑥大于AB的长 ⑦A,B ⑧大于AB的长 ⑨P PM A,B 大于AB的长 平行 垂直 由前向后 由左向右 由上向下 长对正 高平齐 宽相等 实线 虚线
【自我诊断】
1.如图,这是由五个相同的小立方块搭成的几何体,则这个几何体的左视图是 ( )
A B
C D
2.下列四幅图,表示两棵树在同一时刻阳光下的影子是 ( )
A B C D
3.某正方体的每个面上都有一个汉字,如图,这是它的一种表面展开图,那么在原正方体中,与“中”字所在面相对面上的汉字是 ( )
A.故 B.讲 C.国 D.事
4.由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图如图所示,则搭建这个几何体所需要的小正方体的个数可能为 ( )
A.5 B.6 C.5或6 D.6或7
【参考答案】
1.C 2.B 3.D 4.C
【真题精粹】
考向1 投影
1.(拓展)如图,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为 ( )
A.12 cm B.20 cm C.3.2 cm D.10 cm
考向2 三视图(6年4考)
2.(2019·江西)如图,这是由手提水果篮抽象出的几何体,以箭头所指的方向为主视图方向,则它的俯视图为 ( )
A B C D
3.(2021·江西)如图所示的几何体的主视图是 ( )
A B C D
4.(2018·江西)如图所示的几何体的左视图为 ( )
5.(2022·江西)如图,这是由四个完全相同的小正方体搭成的几何体,它的俯视图为 ( )
A B C D
热点预测
6.(劳动实践)某学校组织学生到工厂劳动实践,学习制作机械零件的基本流程,如图,这是一种“工”型液压机的配件,它的俯视图是 ( )
A B C D
考向3 创新作图(必考)
7.(2023·江西)如图,这是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)在图1中作锐角△ABC,使点C在格点上.
(2)在图2中的线段AB上作点Q,使PQ最短.
8.(2018·江西)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度直尺分别按下列要求画图.(保留画图痕迹)
(1)在图1中,画出△ABD中BD边上的中线.
(2)在图2中,若BA=BD,画出△ABD中AD边上的高.
图1 图2
9.(2021·江西)已知正方形ABCD的边长为4个单位长度,E是CD的中点,请仅用无刻度直尺按下列要求作图.(保留作图痕迹)
(1)在图1中,将直线AC绕着正方形ABCD的中心顺时针旋转45°.
(2)在图2中,将直线AC向上平移1个单位长度.
热点预测
10.如图,在5×3的正方形网格中,每个小格的顶点叫作格点,点A,B,C均在格点上,按下列要求画图.
(1)在图1中,画出一个 ABCD,使顶点D在格点上.
(2)在图2中,画出一条线段BE,使BE⊥AC,且点E在格点上.
考向4 立体图形的展开图与折叠(仅2020年考查)
11.(2020·江西)如图,正方体的展开图为 ( )
【参考答案】
1.B 2.A 3.C 4.D 5.A 6.D
7.略 8.略 9.略 10.略 11.A
【核心突破】
考点1 投影
例题1 如图,树AB在路灯O的照射下形成投影AC,若树高AB=2 m,树影AC=3 m,树与路灯的水平距离AP=4.5 m,则路灯的高度OP是 ( )
A.3 m B.4 m C.5 m D.6 m
变式特训1.如图1,随着光伏发电项目投资成本下降,越来越多的“光伏”项目正在逐步走进我们的生活.光伏发电不仅能为城市提供清洁能源,还能减少城市污染和能源消耗.如图2,长BC=8 m,宽AB=1.5 m的太阳能电池板与水平面成30°夹角,经过太阳光的正投影,它在水平面所形成的阴影的面积为 ( )
A.12 m2 B.6 m2
C.6 m2 D. m2
考点2 三视图
例题2(2023·鹰潭模拟) 如图,该几何体的左视图是 ( )
A B C D
变式特训2.(民族文化)江西茶文化源远流长,其历史可追溯到两千年前的秦汉时期.如图,这是江西名茶中一种装茶的罐子及抽象出的立体图形,则其主视图为 ( )
A B C D
3.(古人智慧)在我国古代建筑中经常使用榫卯构件,如图,这是某种榫卯构件的示意图,其中卯的俯视图是 ( )
A B
C D
考点3 立体图形的展开与折叠
例题3(2023·巴中)某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是 ( )
A.传 B.承
C.文 D.化
方法提炼
变式特训4.一个骰子相对两面的点数之和为7,它的展开图如图所示,下列判断正确的是 ( )
A.A代表 B.B代表
C.C代表 D.B代表
5.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则下列序号中不应剪去的是 ( )
A.3 B.2 C.6 D.1
6.三棱柱的展开图不可能是 ( )
A B
C D
考点4 创新作图
例题4 (2023·鹰潭模拟) 图1,图2都是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.请仅用无刻度直尺在网格中完成下列画图.
(1)在图1中,画出△ABC中AB边上的中线CM.
(2)在图2中,画出∠APC,使∠APC=∠ABC,且点P在格点上.(画出一个即可)
变式特训7.已知四边形ABCD为平行四边形,E为AB边的中点,请仅用无刻度直尺分别按下列要求作图.(保留作图痕迹)
(1)在图1中,作出AD边的中点P.
(2)在图2中,在AD边上求作一点M,使△ABM的面积为 ABCD面积的.
8.在图1,图2中,四边形ABCD为矩形,某圆经过A,B两点,请你仅用无刻度直尺分别按下列要求作图.
(1)在图1中画出该圆的圆心O.
(2)在图2中画出线段CD的垂直平分线.
【参考答案】
例题1 C
变式特训
1.C
例题2 B
变式特训
2.D 3.C
例题3 D
变式特训
4.A 5.A 6.D
例题4 略
变式特训
7.略 8.略
2
同课章节目录
