2024年江西中考数学一轮复习考点探究 第5节 相似三角形 学案 (含答案)
文档属性
| 名称 | 2024年江西中考数学一轮复习考点探究 第5节 相似三角形 学案 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 318.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:34:59 | ||
图片预览


文档简介
第5节 相似三角形(必考,3~12分)
命题分析
相似三角形是平面几何中的重要知识点,是考查学生思维的有效载体,单独考查时一般难度较小,但也是江西学考几何压轴题中难度最大的知识点.利用相似三角形求线段的长和线段的比是重要的方法,除了熟练掌握相似的判定方法外,还需要掌握如下一些常见的相似模型:平行线型、斜交型、一线三等角型、双蝴蝶型等,同时还要学会从复杂图形中分离出基本图形,利用基本图形的性质进行解题.
【知识清单】
知识点1 比例线段的相关概念及性质
黄金分割:在线段AB上,点C把线段AB分成两条线段AC和BC(AC>BC),如果=,那么称线段AB被点C黄金分割,C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,黄金比为⑤ ,线段AB有⑥ 个黄金分割点.
知识点2 平行线分线段成比例
知识点3 相似多边形
知识点4 相似三角形
【参考答案】
①ac ②ad ③ ④ ⑤ ⑥2 ⑦成比例
⑧相似比 ⑨相似比 ⑩相似比的平方 相似比 相似比的平方 相似 夹角
【自我诊断】
1.若3a=4b(b≠0),则的值为 ( )
A. B. C. D.
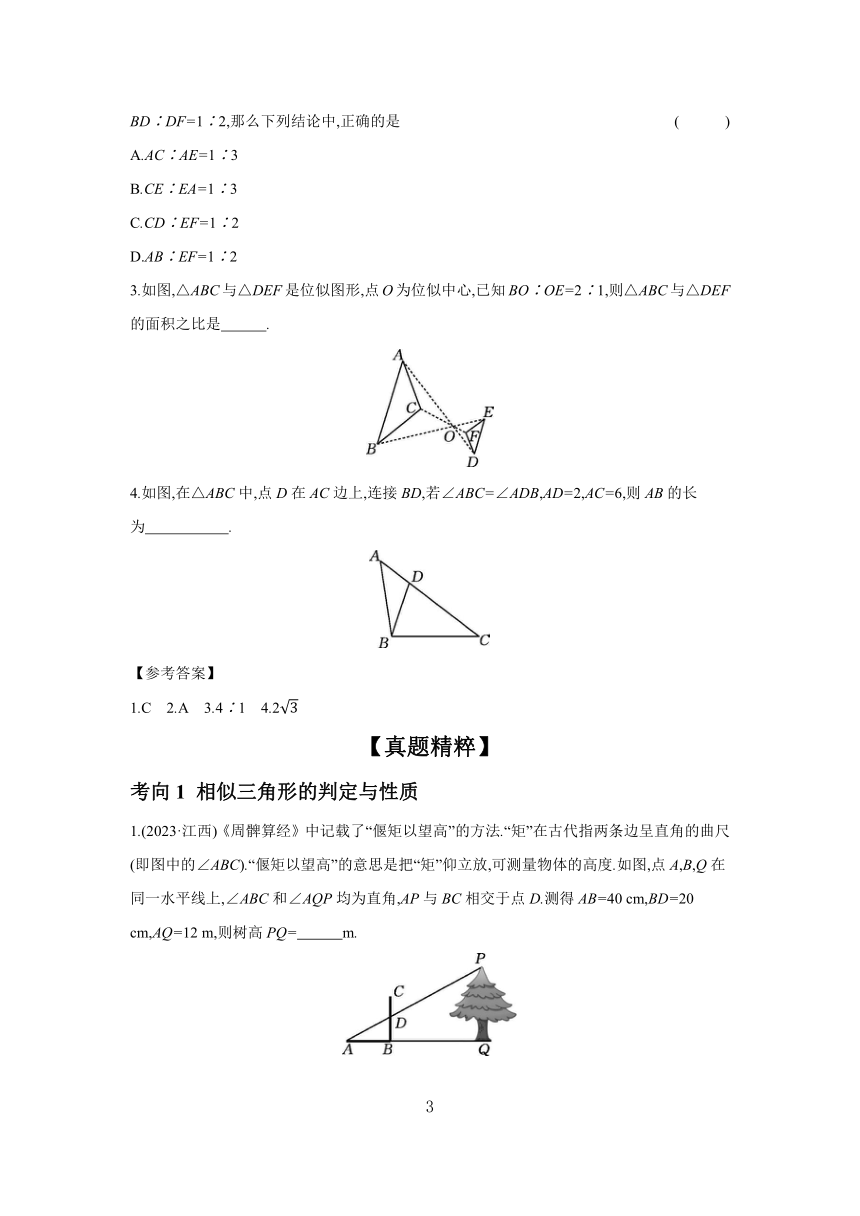
2.如图,已知AB∥CD∥EF,
BD∶DF=1∶2,那么下列结论中,正确的是 ( )
A.AC∶AE=1∶3
B.CE∶EA=1∶3
C.CD∶EF=1∶2
D.AB∶EF=1∶2
3.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO∶OE=2∶1,则△ABC与△DEF的面积之比是 .
4.如图,在△ABC中,点D在AC边上,连接BD,若∠ABC=∠ADB,AD=2,AC=6,则AB的长为 .
【参考答案】
1.C 2.A 3.4∶1 4.2
【真题精粹】
考向1 相似三角形的判定与性质
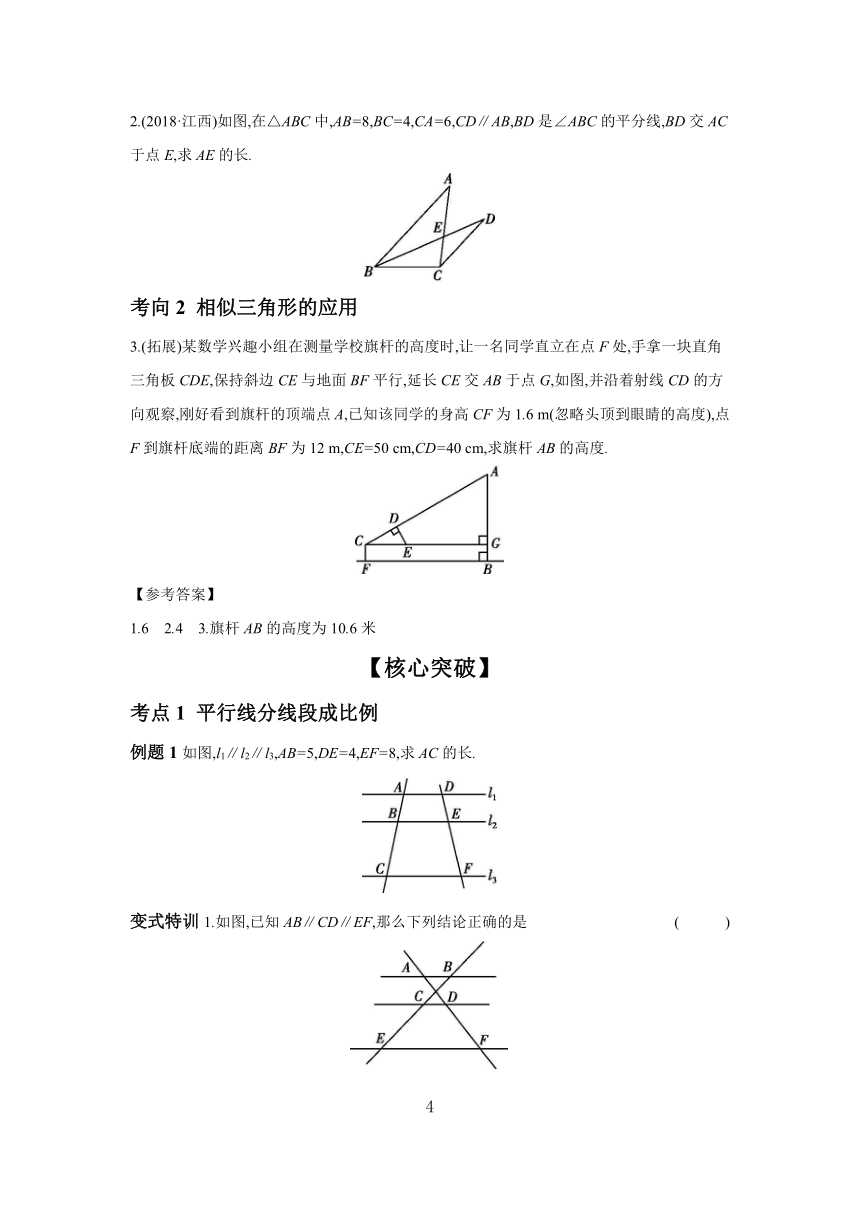
1.(2023·江西)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的∠ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40 cm,BD=20 cm,AQ=12 m,则树高PQ= m.
2.(2018·江西)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
考向2 相似三角形的应用
3.(拓展)某数学兴趣小组在测量学校旗杆的高度时,让一名同学直立在点F处,手拿一块直角三角板CDE,保持斜边CE与地面BF平行,延长CE交AB于点G,如图,并沿着射线CD的方向观察,刚好看到旗杆的顶端点A,已知该同学的身高CF为1.6 m(忽略头顶到眼睛的高度),点F到旗杆底端的距离BF为12 m,CE=50 cm,CD=40 cm,求旗杆AB的高度.
【参考答案】
1.6 2.4 3.旗杆AB的高度为10.6米
【核心突破】
考点1 平行线分线段成比例
例题1如图,l1∥l2∥l3,AB=5,DE=4,EF=8,求AC的长.
变式特训1.如图,已知AB∥CD∥EF,那么下列结论正确的是 ( )
A.=
B.=
C.=
D.=
考点2 相似三角形的性质与判定
一题多设问
例题2如图,在△ABC中,点D,E分别在AC,AB上,且DE∥BC,连接EC和BD,EC和BD相交于点F.
(1)证明:△AED∽△ABC.
(2)若AD=3,CD=4,AE=2,求BE的长.
(3)若ED=5,BC=8,AD=3,求DC的长.
(4)若AD=3,CD=4,求C△AED∶C△ABC的值以及S△AED∶S△ABC的值.
(5)若=,求的值.
(6)若=,S△AED=4,求△ABC的面积.
变式特训2.阅读与思考:
如图,这是两位同学对一道习题的交流情况,请认真阅读下列对话并完成相应的任务.
解决问题:
(1)写出正确的比例式及后续解答.
(2)指出另一个错误,并给出正确解答.
拓展延伸:
(3)如图,已知矩形ABCD的边长AB=3 cm,BC=6 cm.某一时刻,动点M从点A出发沿AB方向以1 cm/s的速度向点B匀速运动;同时,动点N从点D出发沿DA方向以2 cm/s的速度向点A匀速运动.是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似 若存在,直接写出t的值;若不存在,请说明理由.
方法提炼
判定两个三角形相似的常规思考过程:
(1)先找两对对应角相等,一般这个条件比较简单;
(2)若只能找到一对对应角相等,则判断相等角的两夹边是否对应成比例;
(3)若找不到角相等,则判断三边是否对应成比例;
(4)若题目出现平行线,则直接运用基本定理得出相似的三角形.
考点3 相似三角形的应用
例题3如图,昌昌同学和同伴秋游时,发现在某地小山坡的点E处有一棵小树,他们想利用皮尺、量角器和平面镜测量小树到山脚下的距离(即DE的长度),昌昌站在点B处,让同伴移动平面镜至点C处,此时昌昌在平面镜内可以看到点E,且测得BC=3米,CD=28米,∠CDE=150°.已知昌昌的眼睛到地面的距离AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
变式特训3.如图1,这是一个晾衣架,图2是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点在地面上,经测量得到AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段.
(1)连接AC,求证:AC∥EF.
(2)若EF=32 cm,求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上
【参考答案】
例题1 AC=15
变式特训
1.D
例题2 (1)略 (2)BE= (3)DC=
(4)C△AED∶C△ABC=3∶7,S△AED∶S△ABC=9∶49
(5)= (6)S△ABC=25
变式特训
2.(1)=,DE= (2)略
(3)当t=或t=时,以A,M,N为顶点的三角形与△ACD相似
例题3 DE的长度为56(2+)米
变式特训
3.(1)略
(2)利用夹子垂挂在晒衣架上的连衣裙总长度小于120 cm时,连衣裙才不会拖在地面上
2
命题分析
相似三角形是平面几何中的重要知识点,是考查学生思维的有效载体,单独考查时一般难度较小,但也是江西学考几何压轴题中难度最大的知识点.利用相似三角形求线段的长和线段的比是重要的方法,除了熟练掌握相似的判定方法外,还需要掌握如下一些常见的相似模型:平行线型、斜交型、一线三等角型、双蝴蝶型等,同时还要学会从复杂图形中分离出基本图形,利用基本图形的性质进行解题.
【知识清单】
知识点1 比例线段的相关概念及性质
黄金分割:在线段AB上,点C把线段AB分成两条线段AC和BC(AC>BC),如果=,那么称线段AB被点C黄金分割,C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,黄金比为⑤ ,线段AB有⑥ 个黄金分割点.
知识点2 平行线分线段成比例
知识点3 相似多边形
知识点4 相似三角形
【参考答案】
①ac ②ad ③ ④ ⑤ ⑥2 ⑦成比例
⑧相似比 ⑨相似比 ⑩相似比的平方 相似比 相似比的平方 相似 夹角
【自我诊断】
1.若3a=4b(b≠0),则的值为 ( )
A. B. C. D.
2.如图,已知AB∥CD∥EF,
BD∶DF=1∶2,那么下列结论中,正确的是 ( )
A.AC∶AE=1∶3
B.CE∶EA=1∶3
C.CD∶EF=1∶2
D.AB∶EF=1∶2
3.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO∶OE=2∶1,则△ABC与△DEF的面积之比是 .
4.如图,在△ABC中,点D在AC边上,连接BD,若∠ABC=∠ADB,AD=2,AC=6,则AB的长为 .
【参考答案】
1.C 2.A 3.4∶1 4.2
【真题精粹】
考向1 相似三角形的判定与性质
1.(2023·江西)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的∠ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40 cm,BD=20 cm,AQ=12 m,则树高PQ= m.
2.(2018·江西)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
考向2 相似三角形的应用
3.(拓展)某数学兴趣小组在测量学校旗杆的高度时,让一名同学直立在点F处,手拿一块直角三角板CDE,保持斜边CE与地面BF平行,延长CE交AB于点G,如图,并沿着射线CD的方向观察,刚好看到旗杆的顶端点A,已知该同学的身高CF为1.6 m(忽略头顶到眼睛的高度),点F到旗杆底端的距离BF为12 m,CE=50 cm,CD=40 cm,求旗杆AB的高度.
【参考答案】
1.6 2.4 3.旗杆AB的高度为10.6米
【核心突破】
考点1 平行线分线段成比例
例题1如图,l1∥l2∥l3,AB=5,DE=4,EF=8,求AC的长.
变式特训1.如图,已知AB∥CD∥EF,那么下列结论正确的是 ( )
A.=
B.=
C.=
D.=
考点2 相似三角形的性质与判定
一题多设问
例题2如图,在△ABC中,点D,E分别在AC,AB上,且DE∥BC,连接EC和BD,EC和BD相交于点F.
(1)证明:△AED∽△ABC.
(2)若AD=3,CD=4,AE=2,求BE的长.
(3)若ED=5,BC=8,AD=3,求DC的长.
(4)若AD=3,CD=4,求C△AED∶C△ABC的值以及S△AED∶S△ABC的值.
(5)若=,求的值.
(6)若=,S△AED=4,求△ABC的面积.
变式特训2.阅读与思考:
如图,这是两位同学对一道习题的交流情况,请认真阅读下列对话并完成相应的任务.
解决问题:
(1)写出正确的比例式及后续解答.
(2)指出另一个错误,并给出正确解答.
拓展延伸:
(3)如图,已知矩形ABCD的边长AB=3 cm,BC=6 cm.某一时刻,动点M从点A出发沿AB方向以1 cm/s的速度向点B匀速运动;同时,动点N从点D出发沿DA方向以2 cm/s的速度向点A匀速运动.是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似 若存在,直接写出t的值;若不存在,请说明理由.
方法提炼
判定两个三角形相似的常规思考过程:
(1)先找两对对应角相等,一般这个条件比较简单;
(2)若只能找到一对对应角相等,则判断相等角的两夹边是否对应成比例;
(3)若找不到角相等,则判断三边是否对应成比例;
(4)若题目出现平行线,则直接运用基本定理得出相似的三角形.
考点3 相似三角形的应用
例题3如图,昌昌同学和同伴秋游时,发现在某地小山坡的点E处有一棵小树,他们想利用皮尺、量角器和平面镜测量小树到山脚下的距离(即DE的长度),昌昌站在点B处,让同伴移动平面镜至点C处,此时昌昌在平面镜内可以看到点E,且测得BC=3米,CD=28米,∠CDE=150°.已知昌昌的眼睛到地面的距离AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
变式特训3.如图1,这是一个晾衣架,图2是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点在地面上,经测量得到AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段.
(1)连接AC,求证:AC∥EF.
(2)若EF=32 cm,求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上
【参考答案】
例题1 AC=15
变式特训
1.D
例题2 (1)略 (2)BE= (3)DC=
(4)C△AED∶C△ABC=3∶7,S△AED∶S△ABC=9∶49
(5)= (6)S△ABC=25
变式特训
2.(1)=,DE= (2)略
(3)当t=或t=时,以A,M,N为顶点的三角形与△ACD相似
例题3 DE的长度为56(2+)米
变式特训
3.(1)略
(2)利用夹子垂挂在晒衣架上的连衣裙总长度小于120 cm时,连衣裙才不会拖在地面上
2
同课章节目录
