2024年江西中考数学一轮复习考点探究 第6节 解直角三角形及其应用 学案(含答案)
文档属性
| 名称 | 2024年江西中考数学一轮复习考点探究 第6节 解直角三角形及其应用 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:36:46 | ||
图片预览


文档简介
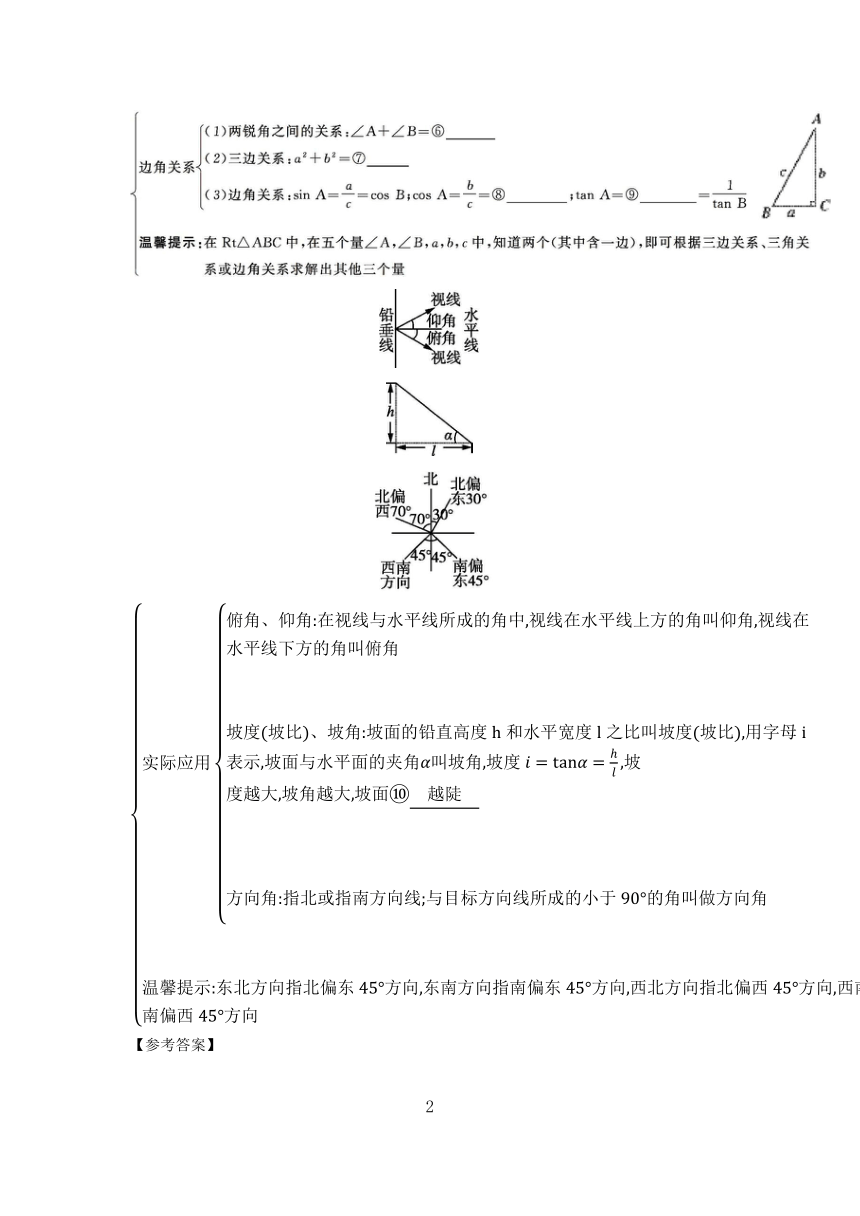
第6节 解直角三角形及其应用(必考,3~11分)
命题分析
解直角三角形的应用是锐角三角函数的重要内容,对于高中阶段的数学及物理的学习也有着重要意义.江西学考近6年每年都有一道两问的实际应用问题,背景为实际生活中常见的以三角形、四边形和圆等为模型的实际物体,第一问往往是考查几何图形的基本性质或判定,第二问则是解直角三角形的实际应用.
【知识清单】
知识点1 锐角三角函数的定义
在Rt△ABC中,∠C=90°,∠A为△ABC中一锐角,sin A==① ;cos A==② ;tan A==③
知识点2 特殊角的三角函数值
30° 45° 60° 基本图形
sin α ④
cos α
tan α ⑤
知识点3 解直角三角形
【参考答案】
① ② ③ ④ ⑤1 ⑥90° ⑦c2 ⑧sin B
⑨ ⑩越陡
【自我诊断】
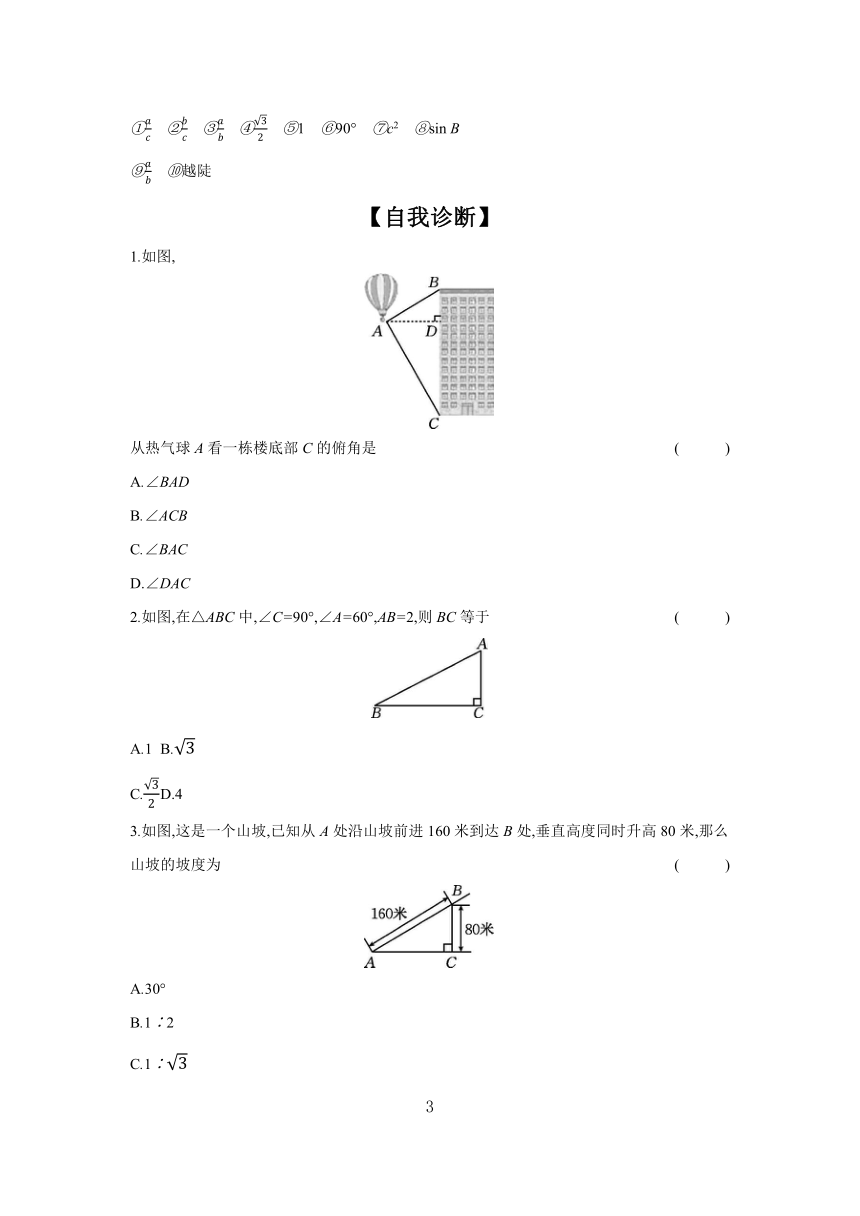
1.如图,
从热气球A看一栋楼底部C的俯角是 ( )
A.∠BAD
B.∠ACB
C.∠BAC
D.∠DAC
2.如图,在△ABC中,∠C=90°,∠A=60°,AB=2,则BC等于 ( )
A.1 B.
C. D.4
3.如图,这是一个山坡,已知从A处沿山坡前进160米到达B处,垂直高度同时升高80米,那么山坡的坡度为 ( )
A.30°
B.1∶2
C.1∶
D.∶1
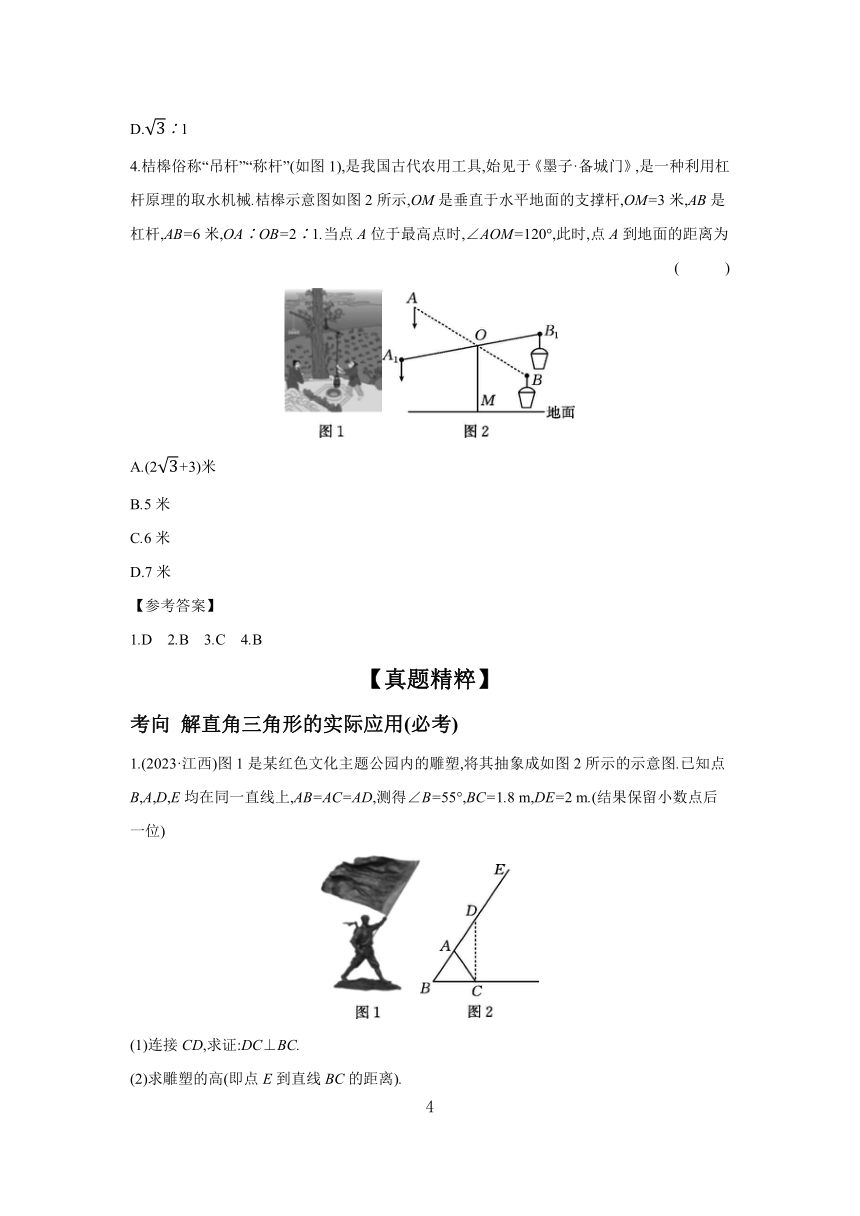
4.桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°,此时,点A到地面的距离为 ( )
A.(2+3)米
B.5米
C.6米
D.7米
【参考答案】
1.D 2.B 3.C 4.B
【真题精粹】
考向 解直角三角形的实际应用(必考)
1.(2023·江西)图1是某红色文化主题公园内的雕塑,将其抽象成如图2所示的示意图.已知点B,A,D,E均在同一直线上,AB=AC=AD,测得∠B=55°,BC=1.8 m,DE=2 m.(结果保留小数点后一位)
(1)连接CD,求证:DC⊥BC.
(2)求雕塑的高(即点E到直线BC的距离).
(参考数据:sin 55°≈0.82,cos 55°≈0.57,tan 55°≈1.43)
2.(2022·江西)图1是某长征主题公园的雕塑,将其抽象成如图2所示的示意图,已知AB∥CD∥FG,A,D,H,G四点在同一直线上,测得∠FEC=∠A=72.9°,AD=1.6 m,EF=6.2 m.(结果保留小数点后一位)
(1)求证:四边形DEFG为平行四边形.
(2)求雕塑的高(即点G到AB的距离).
(参考数据:sin 72.9°≈0.96,cos 72.9°≈0.29,tan 72.9°≈3.25)
3.(2020·江西)图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,量得托板长AB=120 mm,支撑板长CD=80 mm,底座长DE=90 mm,托板AB固定在支撑板顶端点C处,且CB=40 mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位)
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离.
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
(参考数据:sin 40°≈0.643,cos 40°≈0.766,tan 40°≈0.839,sin 26.6°≈0.448,cos 26.6°≈0.894,tan 26.6°≈0.500,≈1.732)
4.(2019·江西)图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8 cm,CD=8 cm,AB=30 cm,BC=35 cm.(结果精确到0.1)
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm时,求∠ABC的大小.
(参考数据:sin 70°≈0.94,cos 20°≈0.94,sin 36.8°≈0.60,cos 53.2°≈0.60)
热点预测
5.某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形ABCD为矩形,AB长6米,AD长2米,点D距离地面0.4米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.
(1)如图2,当道闸打开至∠ADC=60°时,边CD上一点P到地面的距离PE的长为2.4米,求点P到MN的距离PF的长.
(2)一辆载满货物的货车过道闸,已知货车宽2.1米,高3.2米.当道闸打开至∠ADC=53°时,货车能否通过道闸 请说明理由.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
【参考答案】
1.(1)略 (2)雕塑的高约为4.2 m
2.(1)略 (2)雕塑的高约为7.5 m
3.(1)120.7 mm (2)CD旋转的度数约为33.4°
4.(1)①160° ②点D到桌面OE的距离约是27.0 cm
(2)∠ABC=33.2°
5.(1)PF=(6-2)米 (2)货车能通过道闸.理由略
【核心突破】
考点1 在网格中求锐角三角函数值
例题1如图,在网格中,小正方形的边长为1,若点A,B,O都在格点上,则cos∠OAB的值为 ( )
A. B.
C. D.
变式特训1.如图,若点A,B,C在正方
形网格的格点上,则sin∠BAC的值为 ( )
A. B.
C. D.
方法提炼
求锐角函数值的问题必须依托直角三角形,而网格中隐藏着直角及边的数量条件,所以当试题拥有网格这一背景时,要充分利用这一点构建直角三角形,从而计算线段的长,为函数值的计算、勾股定理逆定理以及其他知识的运用准备条件.
考点2 方位角
例题2如图,l是一条笔直的公路,
道路管理部门在点A设置了一个速度监测点,已知BC为公路的一段,B在点A的北偏西30°方向,C在点A的东北方向,若AB=50米,则BC的长为 米.(结果保留根号)
解题指南
(1)根据已知方位角易得AD⊥BC,∠BAD=30°,∠DAC=∠ACD=45°.
(2)在Rt△ADB和Rt△ADC中,根据特殊角求解BD和CD的长,进而求得BC的长.
考点3 坡角、坡度
例题3 如图,某人沿坡角为α的山坡前进了100米,那么他此时与地面的垂直距离BC为 ( )
A.100cos α
B.
C.100sin α
D.
变式特训 2.如图,大坝的横截面是梯形ABCD,AD∥BC,坝顶宽AD=4 m,坝高AE=6 m,斜坡AB的坡度i=1∶,斜坡DC的坡角∠C=45°,那么坝底BC是( )
A.6 m
B.(6+4)m
C.10 m
D.(6+10)m
考点4 解直角三角形的实际应用
例题4(2023·赣州模拟) 每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20 m),且可绕点B转动,其底部B离地面的距离BC为2 m,当云梯顶端A在建筑物EF所在的直线上时,底部B到EF的距离BD为9 m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19 m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处 请说明理由.
(参考数据:sin 53°≈0.8,cos 53°≈0.6,tan 53°≈1.3)
解题指南
(1)在Rt△ABD中,利用锐角三角函数的定义求出AB的长,即可解答.
(2)根据题意可得DE=BC=2 m,从而求出AD=17 m,然后在Rt△ABD中,利用勾股定理求出AB的长,进行比较即可解答.
变式特训3.(优秀传统文化)如图1,一汤碗的截面为轴对称图形(如图2),碗体呈半圆形状(碗体厚度不计),直径EF=26 cm,,碗底AB=10 cm,∠A=∠B=90°,AC=BD=3 cm.
(1)如图1,当汤碗平放在桌面MN上时,碗的高度是 cm,圆心到点B的距离是 cm.
(2)如图2,将碗放在桌面MN上,绕点B缓缓倾斜倒出部分汤,当碗内汤的深度最小时,tan∠ABM的值是 .
4.八一起义纪念碑坐落于江西省南昌市八一广场.1977年八一起义五十周年时破土兴建,1979年1月8日落成.如图,为测量八一起义纪念碑的大致高度AB(AB⊥CD),贝贝在广场平地上的点C处测得纪念碑的顶部的仰角为30°,贝贝又向纪念碑走近了些测量,于点D处的位置测得纪念碑的仰角为75°,测得CD=66米.
(1)求贝贝站在点D处仰望纪念碑顶点A的距离AD的长
(2)求八一起义纪念碑的大致高度AB.
(参考数据:≈1.4,≈1.7,结果精确到0.1米)
5.(2023·抚州模拟)有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的最大伸长距离可达30 cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚轮☉A,☉A与水平地面切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面36 cm时,点C到水平地面的距离CE为54 cm,设AF∥MN.
(1)求☉A的半径长.
(2)当某人的手自然下垂在C端拉旅行箱时,CE为66 cm,∠CAF=53°,求此时拉杆BC的伸长距离.(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,结果精确到1 cm)
【参考答案】
例题1 C
变式特训
1.B
例题2 (25+25)
例题3 C
变式特训
2.D
例题4 (1)此时云梯AB的长为15 m
(2)在该消防车不移动位置的前提下,云梯能伸到险情处.理由略
变式特训
3.(1)15 5 (2)
4.(1)贝贝站在点D处仰望纪念碑顶点A的距离AD约为46.2米
(2)八一起义纪念碑的高度约为44.6米
5.(1)☉A的半径长为6 cm
(2)此时拉杆BC的伸长距离约为25 cm
2
命题分析
解直角三角形的应用是锐角三角函数的重要内容,对于高中阶段的数学及物理的学习也有着重要意义.江西学考近6年每年都有一道两问的实际应用问题,背景为实际生活中常见的以三角形、四边形和圆等为模型的实际物体,第一问往往是考查几何图形的基本性质或判定,第二问则是解直角三角形的实际应用.
【知识清单】
知识点1 锐角三角函数的定义
在Rt△ABC中,∠C=90°,∠A为△ABC中一锐角,sin A==① ;cos A==② ;tan A==③
知识点2 特殊角的三角函数值
30° 45° 60° 基本图形
sin α ④
cos α
tan α ⑤
知识点3 解直角三角形
【参考答案】
① ② ③ ④ ⑤1 ⑥90° ⑦c2 ⑧sin B
⑨ ⑩越陡
【自我诊断】
1.如图,
从热气球A看一栋楼底部C的俯角是 ( )
A.∠BAD
B.∠ACB
C.∠BAC
D.∠DAC
2.如图,在△ABC中,∠C=90°,∠A=60°,AB=2,则BC等于 ( )
A.1 B.
C. D.4
3.如图,这是一个山坡,已知从A处沿山坡前进160米到达B处,垂直高度同时升高80米,那么山坡的坡度为 ( )
A.30°
B.1∶2
C.1∶
D.∶1
4.桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°,此时,点A到地面的距离为 ( )
A.(2+3)米
B.5米
C.6米
D.7米
【参考答案】
1.D 2.B 3.C 4.B
【真题精粹】
考向 解直角三角形的实际应用(必考)
1.(2023·江西)图1是某红色文化主题公园内的雕塑,将其抽象成如图2所示的示意图.已知点B,A,D,E均在同一直线上,AB=AC=AD,测得∠B=55°,BC=1.8 m,DE=2 m.(结果保留小数点后一位)
(1)连接CD,求证:DC⊥BC.
(2)求雕塑的高(即点E到直线BC的距离).
(参考数据:sin 55°≈0.82,cos 55°≈0.57,tan 55°≈1.43)
2.(2022·江西)图1是某长征主题公园的雕塑,将其抽象成如图2所示的示意图,已知AB∥CD∥FG,A,D,H,G四点在同一直线上,测得∠FEC=∠A=72.9°,AD=1.6 m,EF=6.2 m.(结果保留小数点后一位)
(1)求证:四边形DEFG为平行四边形.
(2)求雕塑的高(即点G到AB的距离).
(参考数据:sin 72.9°≈0.96,cos 72.9°≈0.29,tan 72.9°≈3.25)
3.(2020·江西)图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,量得托板长AB=120 mm,支撑板长CD=80 mm,底座长DE=90 mm,托板AB固定在支撑板顶端点C处,且CB=40 mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位)
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离.
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
(参考数据:sin 40°≈0.643,cos 40°≈0.766,tan 40°≈0.839,sin 26.6°≈0.448,cos 26.6°≈0.894,tan 26.6°≈0.500,≈1.732)
4.(2019·江西)图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8 cm,CD=8 cm,AB=30 cm,BC=35 cm.(结果精确到0.1)
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm时,求∠ABC的大小.
(参考数据:sin 70°≈0.94,cos 20°≈0.94,sin 36.8°≈0.60,cos 53.2°≈0.60)
热点预测
5.某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形ABCD为矩形,AB长6米,AD长2米,点D距离地面0.4米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.
(1)如图2,当道闸打开至∠ADC=60°时,边CD上一点P到地面的距离PE的长为2.4米,求点P到MN的距离PF的长.
(2)一辆载满货物的货车过道闸,已知货车宽2.1米,高3.2米.当道闸打开至∠ADC=53°时,货车能否通过道闸 请说明理由.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
【参考答案】
1.(1)略 (2)雕塑的高约为4.2 m
2.(1)略 (2)雕塑的高约为7.5 m
3.(1)120.7 mm (2)CD旋转的度数约为33.4°
4.(1)①160° ②点D到桌面OE的距离约是27.0 cm
(2)∠ABC=33.2°
5.(1)PF=(6-2)米 (2)货车能通过道闸.理由略
【核心突破】
考点1 在网格中求锐角三角函数值
例题1如图,在网格中,小正方形的边长为1,若点A,B,O都在格点上,则cos∠OAB的值为 ( )
A. B.
C. D.
变式特训1.如图,若点A,B,C在正方
形网格的格点上,则sin∠BAC的值为 ( )
A. B.
C. D.
方法提炼
求锐角函数值的问题必须依托直角三角形,而网格中隐藏着直角及边的数量条件,所以当试题拥有网格这一背景时,要充分利用这一点构建直角三角形,从而计算线段的长,为函数值的计算、勾股定理逆定理以及其他知识的运用准备条件.
考点2 方位角
例题2如图,l是一条笔直的公路,
道路管理部门在点A设置了一个速度监测点,已知BC为公路的一段,B在点A的北偏西30°方向,C在点A的东北方向,若AB=50米,则BC的长为 米.(结果保留根号)
解题指南
(1)根据已知方位角易得AD⊥BC,∠BAD=30°,∠DAC=∠ACD=45°.
(2)在Rt△ADB和Rt△ADC中,根据特殊角求解BD和CD的长,进而求得BC的长.
考点3 坡角、坡度
例题3 如图,某人沿坡角为α的山坡前进了100米,那么他此时与地面的垂直距离BC为 ( )
A.100cos α
B.
C.100sin α
D.
变式特训 2.如图,大坝的横截面是梯形ABCD,AD∥BC,坝顶宽AD=4 m,坝高AE=6 m,斜坡AB的坡度i=1∶,斜坡DC的坡角∠C=45°,那么坝底BC是( )
A.6 m
B.(6+4)m
C.10 m
D.(6+10)m
考点4 解直角三角形的实际应用
例题4(2023·赣州模拟) 每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20 m),且可绕点B转动,其底部B离地面的距离BC为2 m,当云梯顶端A在建筑物EF所在的直线上时,底部B到EF的距离BD为9 m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19 m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处 请说明理由.
(参考数据:sin 53°≈0.8,cos 53°≈0.6,tan 53°≈1.3)
解题指南
(1)在Rt△ABD中,利用锐角三角函数的定义求出AB的长,即可解答.
(2)根据题意可得DE=BC=2 m,从而求出AD=17 m,然后在Rt△ABD中,利用勾股定理求出AB的长,进行比较即可解答.
变式特训3.(优秀传统文化)如图1,一汤碗的截面为轴对称图形(如图2),碗体呈半圆形状(碗体厚度不计),直径EF=26 cm,,碗底AB=10 cm,∠A=∠B=90°,AC=BD=3 cm.
(1)如图1,当汤碗平放在桌面MN上时,碗的高度是 cm,圆心到点B的距离是 cm.
(2)如图2,将碗放在桌面MN上,绕点B缓缓倾斜倒出部分汤,当碗内汤的深度最小时,tan∠ABM的值是 .
4.八一起义纪念碑坐落于江西省南昌市八一广场.1977年八一起义五十周年时破土兴建,1979年1月8日落成.如图,为测量八一起义纪念碑的大致高度AB(AB⊥CD),贝贝在广场平地上的点C处测得纪念碑的顶部的仰角为30°,贝贝又向纪念碑走近了些测量,于点D处的位置测得纪念碑的仰角为75°,测得CD=66米.
(1)求贝贝站在点D处仰望纪念碑顶点A的距离AD的长
(2)求八一起义纪念碑的大致高度AB.
(参考数据:≈1.4,≈1.7,结果精确到0.1米)
5.(2023·抚州模拟)有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的最大伸长距离可达30 cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚轮☉A,☉A与水平地面切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面36 cm时,点C到水平地面的距离CE为54 cm,设AF∥MN.
(1)求☉A的半径长.
(2)当某人的手自然下垂在C端拉旅行箱时,CE为66 cm,∠CAF=53°,求此时拉杆BC的伸长距离.(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,结果精确到1 cm)
【参考答案】
例题1 C
变式特训
1.B
例题2 (25+25)
例题3 C
变式特训
2.D
例题4 (1)此时云梯AB的长为15 m
(2)在该消防车不移动位置的前提下,云梯能伸到险情处.理由略
变式特训
3.(1)15 5 (2)
4.(1)贝贝站在点D处仰望纪念碑顶点A的距离AD约为46.2米
(2)八一起义纪念碑的高度约为44.6米
5.(1)☉A的半径长为6 cm
(2)此时拉杆BC的伸长距离约为25 cm
2
同课章节目录
