2024年江西中考数学一轮复习考点探究 第7节 二次函数解析式的确定及图象的变换 学案(含答案)
文档属性
| 名称 | 2024年江西中考数学一轮复习考点探究 第7节 二次函数解析式的确定及图象的变换 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 419.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 10:37:32 | ||
图片预览


文档简介
第7节 二次函数解析式的确定及图象的变换
(6年4考,均在二次函数综合题中考查)
命题分析
二次函数图象的变换与解析式的确定是二次函数的重要内容,在江西学考中一般不会单独考查,会融合在二次函数综合题中.
【知识清单】
知识点1 二次函数表达式的确定
二次函数表达式的三种形式
知识点2 二次函数图象的变换
【自我诊断】
1.将二次函数y=x2-2x-1化成y=a(x-h)2+k的形式,正确的是 ( )
A.y=(x-2)2+2 B.y=(x-1)2-2
C.y=(x+1)2+2 D.y=(x-1)2+4
2.将抛物线y=(x-2)2+3向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线为 ( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=(x+1)2+5 D.y=(x+3)2-2
3.小聪在画一个二次函数的图象时,列出了下面几组y与x的对应值:
x … 0 1 2 3 4 5 …
y … 5 0 -3 -4 -3 0 …
该二次函数的解析式是 .
4.将抛物线y=2x2+4绕顶点旋转180°,则旋转后的抛物线的解析式为 .
【参考答案】1.B 2.B 3.y=x2-6x+5 4.y=-2x2+4
【真题精粹】
考向1 二次函数解析式的确定
1.(2023·江西)综合与实践
问题提出
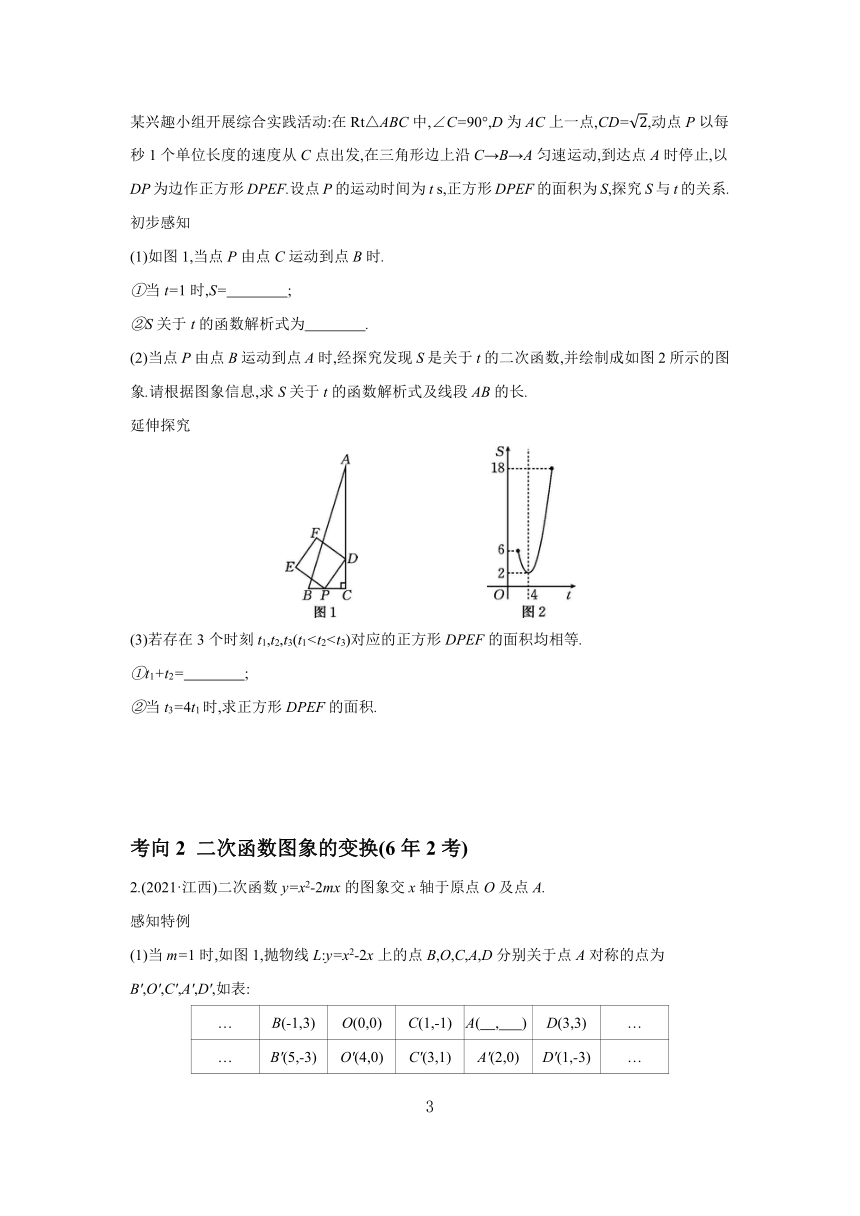
某兴趣小组开展综合实践活动:在Rt△ABC中,∠C=90°,D为AC上一点,CD=,动点P以每秒1个单位长度的速度从C点出发,在三角形边上沿C→B→A匀速运动,到达点A时停止,以DP为边作正方形DPEF.设点P的运动时间为t s,正方形DPEF的面积为S,探究S与t的关系.
初步感知
(1)如图1,当点P由点C运动到点B时.
①当t=1时,S= ;
②S关于t的函数解析式为 .
(2)当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象.请根据图象信息,求S关于t的函数解析式及线段AB的长.
延伸探究
(3)若存在3个时刻t1,t2,t3(t1①t1+t2= ;
②当t3=4t1时,求正方形DPEF的面积.
考向2 二次函数图象的变换(6年2考)
2.(2021·江西)二次函数y=x2-2mx的图象交x轴于原点O及点A.
感知特例
(1)当m=1时,如图1,抛物线L:y=x2-2x上的点B,O,C,A,D分别关于点A对称的点为B',O',C',A',D',如表:
… B(-1,3) O(0,0) C(1,-1) A( , ) D(3,3) …
… B'(5,-3) O'(4,0) C'(3,1) A'(2,0) D'(1,-3) …
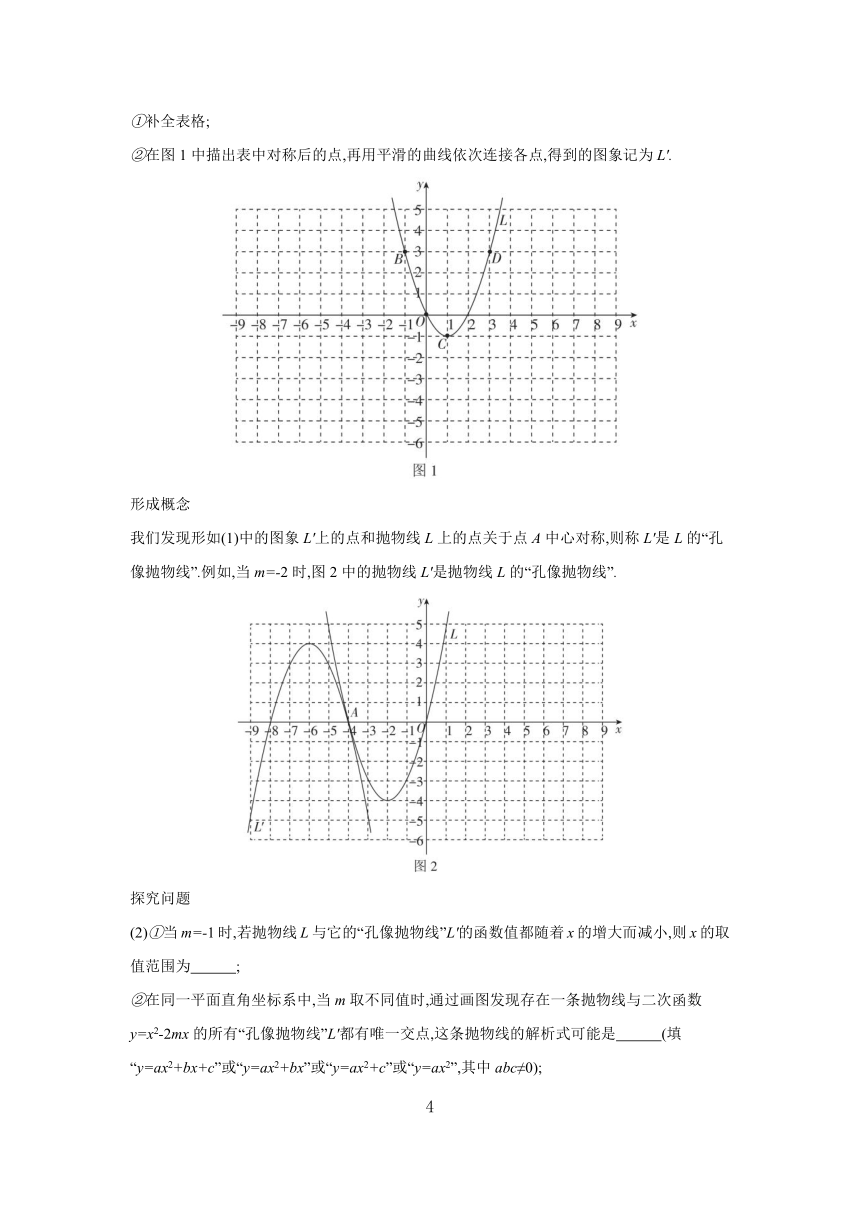
①补全表格;
②在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为L'.
形成概念
我们发现形如(1)中的图象L'上的点和抛物线L上的点关于点A中心对称,则称L'是L的“孔像抛物线”.例如,当m=-2时,图2中的抛物线L'是抛物线L的“孔像抛物线”.
探究问题
(2)①当m=-1时,若抛物线L与它的“孔像抛物线”L'的函数值都随着x的增大而减小,则x的取值范围为 ;
②在同一平面直角坐标系中,当m取不同值时,通过画图发现存在一条抛物线与二次函数y=x2-2mx的所有“孔像抛物线”L'都有唯一交点,这条抛物线的解析式可能是 (填“y=ax2+bx+c”或“y=ax2+bx”或“y=ax2+c”或“y=ax2”,其中abc≠0);
③若二次函数y=x2-2mx及它的“孔像抛物线”与直线y=m有且只有三个交点,求m的值.
【参考答案】1.(1)①3 ②S=t2+2
(2)S=t2-8t+18(2≤t≤8) AB=6
(3)①4 ②S=
2.(1)①(2,0) ②略
(2)①-3≤x≤-1 ②y=ax2 ③m=±1
【核心突破】
考点1 二次函数解析式的确定
例题1 如图,抛物线y=ax2+bx+4经过A(-1,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式.
(2)连接BC,求直线BC的解析式.
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值.
(4)M为x轴上一动点,在抛物线上是否存在一点N,使得以A,C,M,N四点为顶点的四边形是平行四边形 若存在,求出点N的坐标;若不存在,请说明理由.
解题指南
(1)利用待定系数法解决问题即可.
(2)设BC的解析式为y=kx+n,把B,C两点的坐标代入,转化为方程组解决问题即可.
(3)可以连接BC交直线x=于点P,连接PA,此时PA+PC的值最小,最小值为线段BC的长.
(4)观察图象可知,满足条件的点N的纵坐标为4或-4,把问题转化为解方程求解即可.
变式特训 1.(2023·宁波中考)如图,已知二次函数y=x2+bx+c的图象经过点A(1,-2)和B(0,-5).
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当y≤-2时,请根据图象直接写出x的取值范围.
考点2 二次函数图象的变换
例题2 抛物线的函数表达式为y=3(x-2)2+1,若将x轴向上平移2个单位长度,将y轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为 ( )
A.y=3(x+1)2+3
B.y=3(x-5)2+3
C.y=3(x-5)2-1
D.y=3(x+1)2-1
例题3 如图,抛物线C1与x轴交于A(4,0),B(-1,0)两点,与y轴交于点C(0,2).将抛物线C1向右平移m(m>0)个单位长度得到抛物线C2,C2与x轴交于D,E两点(点D在点E的左侧),与抛物线C1在第一象限交于点M.
(1)求抛物线C1的解析式,并求出其对称轴.
(2)①当m=1时,求出抛物线C2的解析式;
②直接写出用含m的代数式表示点M的坐标.
(3)连接DM,AM.在抛物线C1平移的过程中,是否存在△ADM是等边三角形的情况 若存在,请求出此时m的值;若不存在,请说明理由.
变式特训 2.如图,二次函数C1:y=x2+bx+c的图象与x轴分别交于点A,B(点A在点B的左边),|AB|=5,且其顶点的横坐标为.
(1)求二次函数C1的解析式.
(2)如图,将该二次函数在x轴下方的图象沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新的函数C2.
①求函数C2的解析式;
②当直线y=-x+m与新图象有4个交点时,求m的取值范围.
【参考答案】例题1 (1)y=-x2+3x+4
(2)直线BC的解析式为y=-x+4
(3)PA+PC的最小值为4,P,
(4)存在,点N的坐标为(3,4)或,-4或,-4
变式特训
1.(1)二次函数的表达式为y=x2+2x-5,顶点坐标为(-1,-6) (2)-3≤x≤1
例题2 C
例题3 (1)抛物线C1的解析式为y1=-x2+x+2,对称轴是直线x=
(2)①抛物线C2的解析式为y2=-x2+x
②M,
(3)存在.m=4-5
变式特训
2.(1)y=x2-x-6
(2)①C2的解析式为y=
②32
(6年4考,均在二次函数综合题中考查)
命题分析
二次函数图象的变换与解析式的确定是二次函数的重要内容,在江西学考中一般不会单独考查,会融合在二次函数综合题中.
【知识清单】
知识点1 二次函数表达式的确定
二次函数表达式的三种形式
知识点2 二次函数图象的变换
【自我诊断】
1.将二次函数y=x2-2x-1化成y=a(x-h)2+k的形式,正确的是 ( )
A.y=(x-2)2+2 B.y=(x-1)2-2
C.y=(x+1)2+2 D.y=(x-1)2+4
2.将抛物线y=(x-2)2+3向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线为 ( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=(x+1)2+5 D.y=(x+3)2-2
3.小聪在画一个二次函数的图象时,列出了下面几组y与x的对应值:
x … 0 1 2 3 4 5 …
y … 5 0 -3 -4 -3 0 …
该二次函数的解析式是 .
4.将抛物线y=2x2+4绕顶点旋转180°,则旋转后的抛物线的解析式为 .
【参考答案】1.B 2.B 3.y=x2-6x+5 4.y=-2x2+4
【真题精粹】
考向1 二次函数解析式的确定
1.(2023·江西)综合与实践
问题提出
某兴趣小组开展综合实践活动:在Rt△ABC中,∠C=90°,D为AC上一点,CD=,动点P以每秒1个单位长度的速度从C点出发,在三角形边上沿C→B→A匀速运动,到达点A时停止,以DP为边作正方形DPEF.设点P的运动时间为t s,正方形DPEF的面积为S,探究S与t的关系.
初步感知
(1)如图1,当点P由点C运动到点B时.
①当t=1时,S= ;
②S关于t的函数解析式为 .
(2)当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象.请根据图象信息,求S关于t的函数解析式及线段AB的长.
延伸探究
(3)若存在3个时刻t1,t2,t3(t1
②当t3=4t1时,求正方形DPEF的面积.
考向2 二次函数图象的变换(6年2考)
2.(2021·江西)二次函数y=x2-2mx的图象交x轴于原点O及点A.
感知特例
(1)当m=1时,如图1,抛物线L:y=x2-2x上的点B,O,C,A,D分别关于点A对称的点为B',O',C',A',D',如表:
… B(-1,3) O(0,0) C(1,-1) A( , ) D(3,3) …
… B'(5,-3) O'(4,0) C'(3,1) A'(2,0) D'(1,-3) …
①补全表格;
②在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为L'.
形成概念
我们发现形如(1)中的图象L'上的点和抛物线L上的点关于点A中心对称,则称L'是L的“孔像抛物线”.例如,当m=-2时,图2中的抛物线L'是抛物线L的“孔像抛物线”.
探究问题
(2)①当m=-1时,若抛物线L与它的“孔像抛物线”L'的函数值都随着x的增大而减小,则x的取值范围为 ;
②在同一平面直角坐标系中,当m取不同值时,通过画图发现存在一条抛物线与二次函数y=x2-2mx的所有“孔像抛物线”L'都有唯一交点,这条抛物线的解析式可能是 (填“y=ax2+bx+c”或“y=ax2+bx”或“y=ax2+c”或“y=ax2”,其中abc≠0);
③若二次函数y=x2-2mx及它的“孔像抛物线”与直线y=m有且只有三个交点,求m的值.
【参考答案】1.(1)①3 ②S=t2+2
(2)S=t2-8t+18(2≤t≤8) AB=6
(3)①4 ②S=
2.(1)①(2,0) ②略
(2)①-3≤x≤-1 ②y=ax2 ③m=±1
【核心突破】
考点1 二次函数解析式的确定
例题1 如图,抛物线y=ax2+bx+4经过A(-1,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式.
(2)连接BC,求直线BC的解析式.
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值.
(4)M为x轴上一动点,在抛物线上是否存在一点N,使得以A,C,M,N四点为顶点的四边形是平行四边形 若存在,求出点N的坐标;若不存在,请说明理由.
解题指南
(1)利用待定系数法解决问题即可.
(2)设BC的解析式为y=kx+n,把B,C两点的坐标代入,转化为方程组解决问题即可.
(3)可以连接BC交直线x=于点P,连接PA,此时PA+PC的值最小,最小值为线段BC的长.
(4)观察图象可知,满足条件的点N的纵坐标为4或-4,把问题转化为解方程求解即可.
变式特训 1.(2023·宁波中考)如图,已知二次函数y=x2+bx+c的图象经过点A(1,-2)和B(0,-5).
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当y≤-2时,请根据图象直接写出x的取值范围.
考点2 二次函数图象的变换
例题2 抛物线的函数表达式为y=3(x-2)2+1,若将x轴向上平移2个单位长度,将y轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为 ( )
A.y=3(x+1)2+3
B.y=3(x-5)2+3
C.y=3(x-5)2-1
D.y=3(x+1)2-1
例题3 如图,抛物线C1与x轴交于A(4,0),B(-1,0)两点,与y轴交于点C(0,2).将抛物线C1向右平移m(m>0)个单位长度得到抛物线C2,C2与x轴交于D,E两点(点D在点E的左侧),与抛物线C1在第一象限交于点M.
(1)求抛物线C1的解析式,并求出其对称轴.
(2)①当m=1时,求出抛物线C2的解析式;
②直接写出用含m的代数式表示点M的坐标.
(3)连接DM,AM.在抛物线C1平移的过程中,是否存在△ADM是等边三角形的情况 若存在,请求出此时m的值;若不存在,请说明理由.
变式特训 2.如图,二次函数C1:y=x2+bx+c的图象与x轴分别交于点A,B(点A在点B的左边),|AB|=5,且其顶点的横坐标为.
(1)求二次函数C1的解析式.
(2)如图,将该二次函数在x轴下方的图象沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新的函数C2.
①求函数C2的解析式;
②当直线y=-x+m与新图象有4个交点时,求m的取值范围.
【参考答案】例题1 (1)y=-x2+3x+4
(2)直线BC的解析式为y=-x+4
(3)PA+PC的最小值为4,P,
(4)存在,点N的坐标为(3,4)或,-4或,-4
变式特训
1.(1)二次函数的表达式为y=x2+2x-5,顶点坐标为(-1,-6) (2)-3≤x≤1
例题2 C
例题3 (1)抛物线C1的解析式为y1=-x2+x+2,对称轴是直线x=
(2)①抛物线C2的解析式为y2=-x2+x
②M,
(3)存在.m=4-5
变式特训
2.(1)y=x2-x-6
(2)①C2的解析式为y=
②3
同课章节目录
