中考复习课件—方程思想和分类思想

课件36张PPT。九年级数学辅导 训 练 题
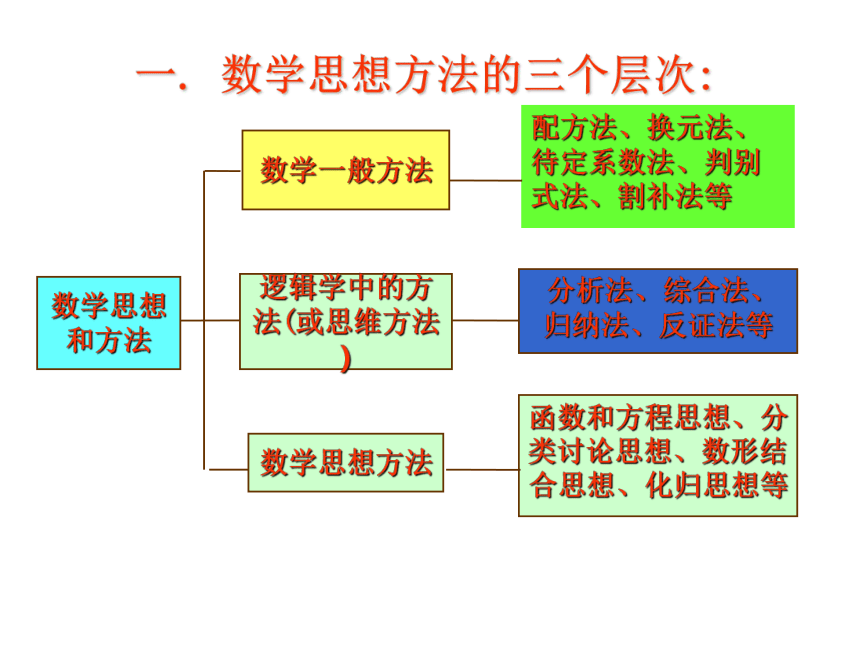
（一）一. 数学思想方法的三个层次: 一.数学的方程思想
方程和方程组是解决应用题、实际问题和许多方面的数学问题的重要基础知识，应用范围非常广泛。很多数学问题，特别是有未知数的几何问题，就需要用方程或方程组的知识来解决，在解决问题时，把某个未知量设为未知数，根据有关的性质、定理或公式，建立起未知数和已知数间的等量关系，列出方程或方程组来解决，这就是方程思想。具有方程思想就能够很好地求得问题中的未知元素或未知量，这对解决和计算有关的数学问题，特别是综合题，是非常需要的。1.若单项式2am+2nbn-2m+2与a5b7 是同类项，则nm的值是( )
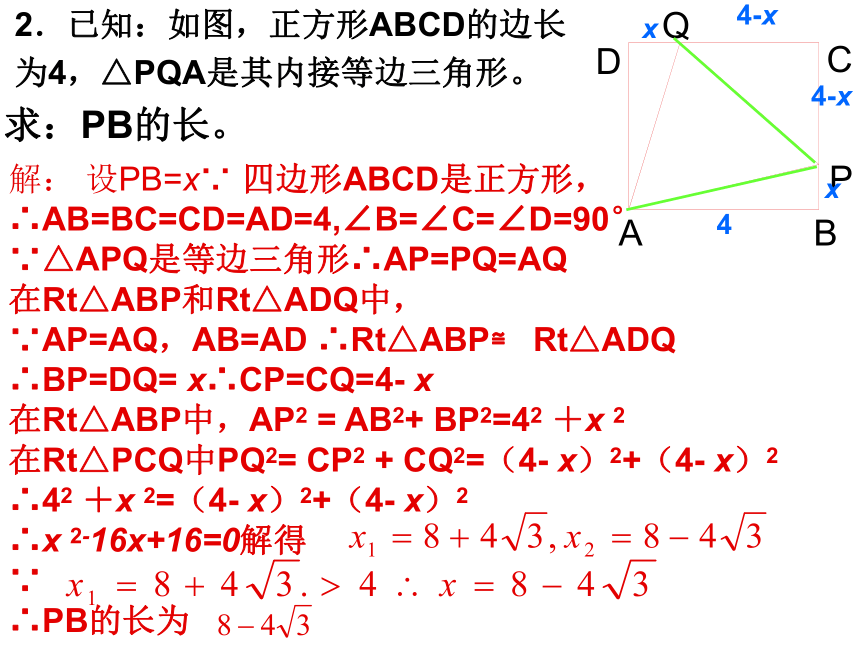
A.-3 B.-1 C.1/3 D.3C【分析】据同类项的定义，运用方程的思想即可求得.解： ，故选择C.2．已知：如图，正方形ABCD的边长
为4，△PQA是其内接等边三角形。
求：PB的长。解： 设PB=x∵ 四边形ABCD是正方形，
∴AB=BC=CD=AD=4,∠B=∠C=∠D=90°
∵△APQ是等边三角形∴AP=PQ=AQ
在Rt△ABP和Rt△ADQ中，
∵AP=AQ，AB=AD ∴Rt△ABP≌ Rt△ADQ
∴BP=DQ= x∴CP=CQ=4- x
在Rt△ABP中，AP2 = AB2+ BP2=42 ＋x 2
在Rt△PCQ中PQ2= CP2 + CQ2=（4- x）2+（4- x）2
∴42 ＋x 2=（4- x）2+（4- x）2
∴x 2-16x+16=0解得
∵
∴PB的长为x44-x
4-x
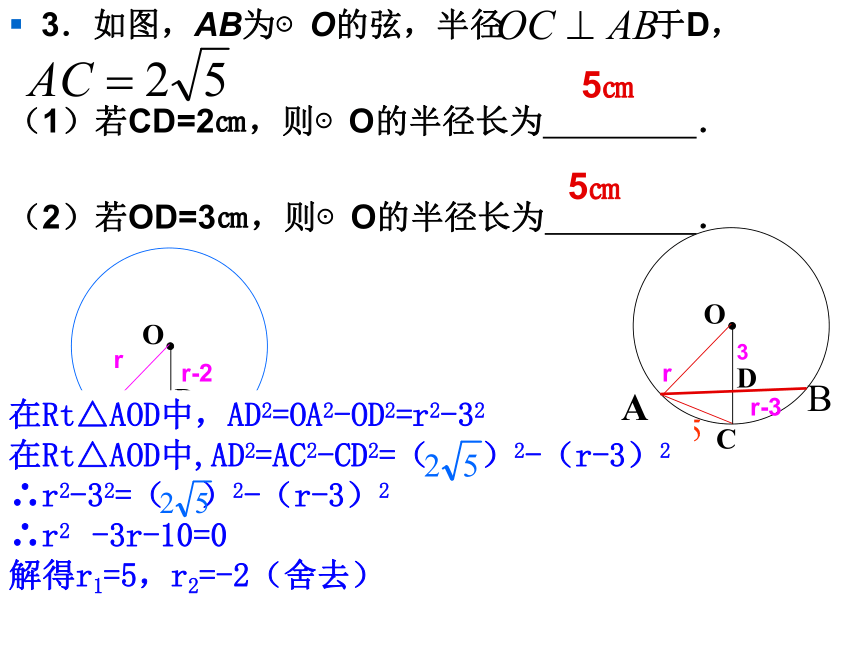
x3．如图，AB为⊙O的弦，半径 于D，
（1）若CD=2㎝，则⊙O的半径长为 ．

（2）若OD=3㎝，则⊙O的半径长为 ．rr-22在Rt△AOD中，AD2=OA2-OD2=r2-（r-2）2
在Rt△AOD中，AD2=AC2-CD2=（ ）2-22
∴r2-（r-2）2=（ ）2-22
∴r=55㎝在Rt△AOD中，AD2=OA2-OD2=r2-32
在Rt△AOD中,AD2=AC2-CD2=（ ）2-（r-3）2
∴r2-32=（ ）2-（r-3）2
∴r2 -3r-10=0
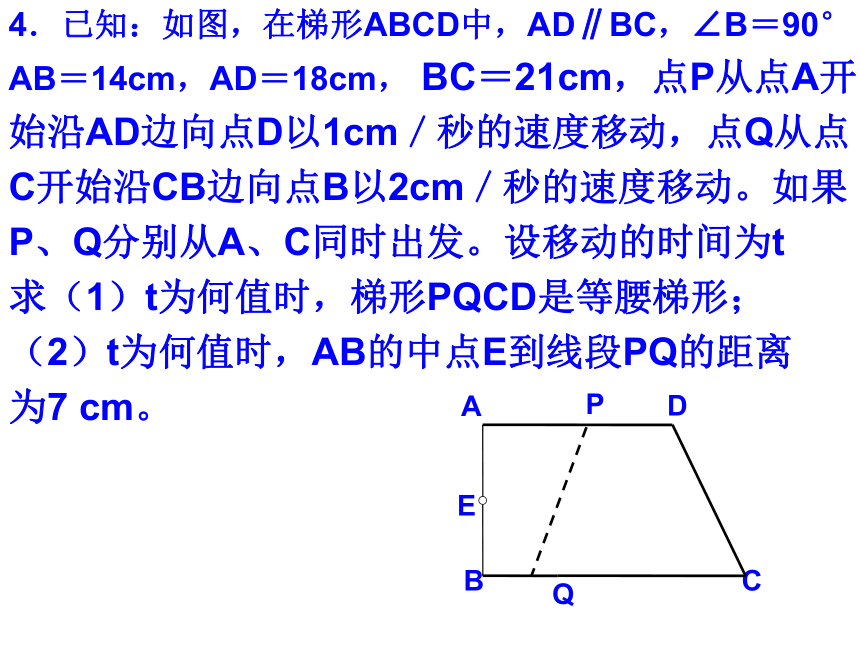
解得r1=5，r2=-2（舍去）3rr-35㎝4．已知：如图，在梯形ABCD中，AD∥BC，∠B＝90°
AB＝14cm，AD＝18cm， BC＝21cm，点P从点A开
始沿AD边向点D以1cm／秒的速度移动，点Q从点
C开始沿CB边向点B以2cm／秒的速度移动。如果
P、Q分别从A、C同时出发。设移动的时间为t
求（1）t为何值时，梯形PQCD是等腰梯形；
（2）t为何值时，AB的中点E到线段PQ的距离
为7 cm。2118142tt21-2tMN33（1）t为何值时，梯形PQCD是等腰梯形；解：分别过P、D作PM⊥BC于，
DN⊥BC于N，得到矩形
ABND和矩形ABMP
∴AP=BM=t，BN=AD=18，∴CN=BC-BN=21-18=3
当梯形PQCD是等腰梯形时，PQ=DC，∠PQM=∠C
∵∠PMQ=∠DNC=90°
∴△PQD≌△DCN
∴QM=CN=3㎝
∵BQ=BC-CQ=21-2t,
∴QM=BM-BQ=t-（21-2t）=3t-21
∴3t-21=3∴t=8（秒）
∴当t为8秒时，梯形PQCD是等腰梯形；PA142tt21-2tMN3t-2114（2）t为何值时，AB的中点E到线段PQ的距离为7 cm。F（2）过E作EF ⊥ PQ于F,
连结PE,EQ，当EF=7㎝时。
∵AE=BE= AB= ×14=7（㎝）
∴AE=EF=BE，
∵AD∥BC，∠B＝90°
∴∠A＝90°
∵PE=PE,EQ=EQ∴Rt△AEP≌Rt△FEP，
Rt△BEQ ≌ Rt△FEQ
∴PA=PF=t，BQ=FQ=21-2t∴PQ=PF+FQ=21-t
在Rt△PQM中，PM=14,QM=3t- 1
∵PM2+QM2=PQ2∴142+（3t-21）2=（21-t）2
解得t1= ，t2=7
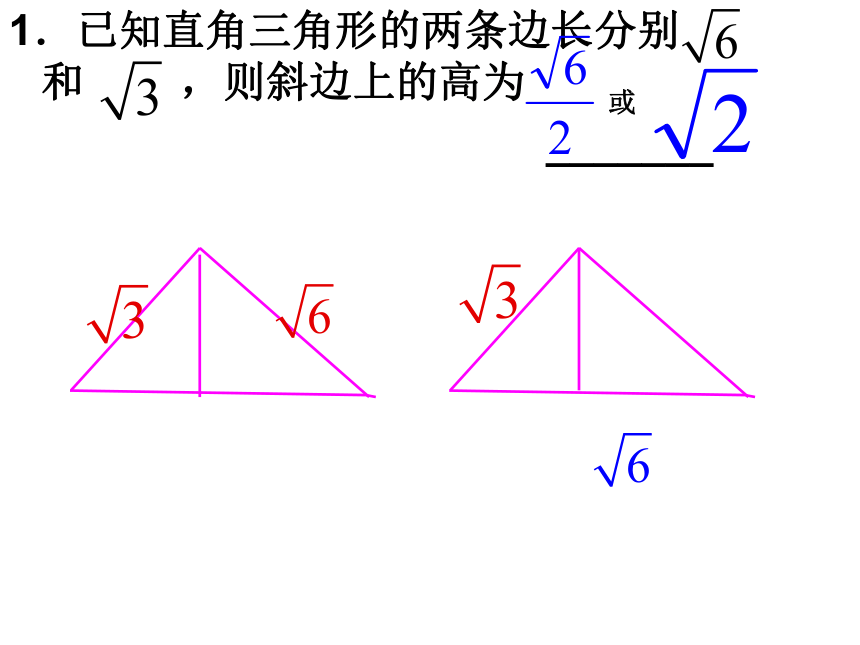
∴当t为 或7时，AB的中点E到线段PQ的距离为7 cm。二、分类讨论思想：在解答某些数学问题时,因为存在一些不确定的因素,解答无法用统一的方法或结论不能给出统一的表述,对这类问题依情况加以分类,并逐类求解,然后综合求解,这种解题的方法叫分类讨论法,它是一种极其重要的数学思想方法.分类讨论设计全部初中数学的知识点，其关键是要弄清楚引起分类的原因，明确分类讨论的对象和标准，应该按可能出现的情况做出既不重复，又不遗漏，分门别类加以讨论求解，再将不同结论综合归纳，得出正确答案。1．已知直角三角形的两条边长分别 和 ，则斜边上的高为
_______
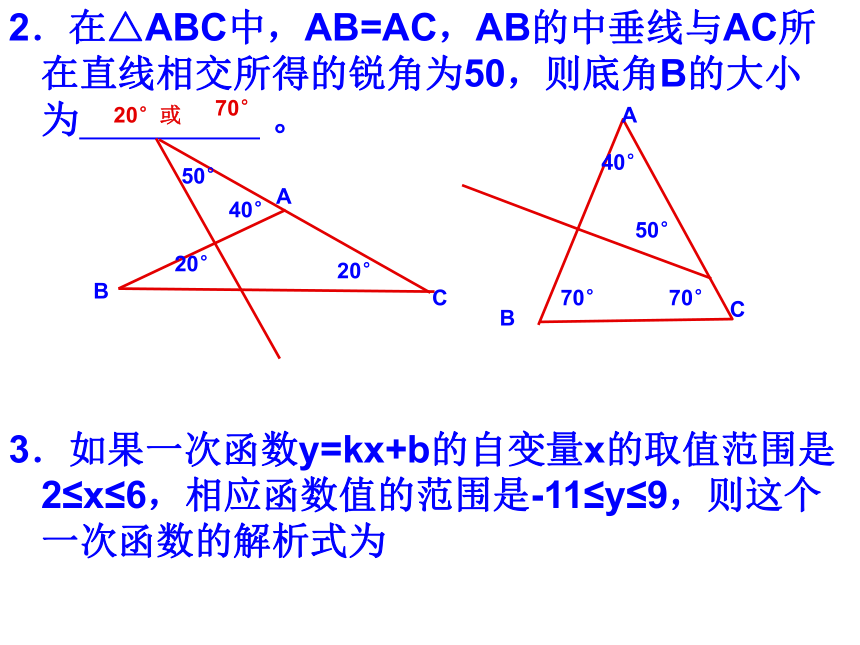
或2．在△ABC中，AB=AC，AB的中垂线与AC所在直线相交所得的锐角为50，则底角B的大小为 。
3．如果一次函数y=kx+b的自变量x的取值范围是 2≤x≤6，相应函数值的范围是-11≤y≤9，则这个一次函数的解析式为 ABCABC50°50°40°40°20°20°70°70°20°或70°3．如果一次函数y=kx+b的自变量x的取值范围是 2≤x≤6，相应函数值的范围是-11≤y≤9，则这个一次函数的解析式为__________. 解：（1）当k>0时，y=kx+b中，y随x的增大而增大， 　　∴ x=-2时，y=-11, ∴x=6时，y=9, ∴ , ∴ , 　　
∴ 函数解析式为y= x-6。 （2）当k<0时，y=kx+b中，y随x的增大而减小， 　　∴ x=-2时，y=9，x=6时，y=-11。 　　∴ , ∴ 　　

∴ y=- x+4。
∴综上（1）（2），所求函数解析式为y= x-6或y=- x+4。 y= x-6或y=- x+44.关于x 的方程kx2－4x－3=0有实数根，则k的值为__________. 本题首先要考虑到的x2系数是字母k，因此要对字母k 讨论：
①当k =0时，原方程为一元一次方程，它有实数根x= ，所以k=0；
②当k≠0时，原方程为一元二次方程，要使它有实数根，则△≥0，得到k≥，所以k≥且k≠0；综合①、②得到k的取值为k≥k≥5.已知△ABC内接于⊙O且AB＝AC，⊙O的半径等于6cm，O点到BC的距离OD等于2cm，则AB的长为 。ABCODD4266266．国家规定个人发表文章，出版图书获得稿费的纳税计算办法是： （1）稿费不高于800元的不纳税 （2）稿费高于800元又不高于4000元的应缴纳超过800元那部分稿费的14%。 （3）稿费高于4000元应缴纳全部稿费的12%的税，今知丁老师获得一笔稿费，并缴纳个人所得税a(a>0)元，求丁老师这笔稿费有多少元。 解：设丁老师这笔稿费为x元，∵a>0, ∴x>800, （1）当8000, ∴x>800, （1）当8004000时，丁老师所纳税x·12%元， 　　
∴ 12%x=a, ∴x= a, 　∴ a>4000, a>480。 　　 即a>480时，x= a= a。 答：当丁老师所纳税a(元)不超过448元时，丁老师的稿费是( a+800)元，当丁老师所纳税a(元)超过480元时， 丁老师获得的稿费是 a。 7.在下图三角形的边上找出一点，使得该点与
三角形的两顶点构成等腰三角形！1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论CABACB20°20°20°20°（分类讨论）　8.如图，线段OD的一个端点O在直线a上，以OD为一边画等腰三角形，并且使另一个顶点在直线a上，这样的等腰三角形能画多少个?ＯＤ150°⌒ＣaＥＦＨ9. 如图，直线AB经过圆O的圆心，与圆O交于A、B两点，点C在O上，且∠AOC=30度，点P是直线AB上的一个动点（与点O不重合），直线PC与圆O相交于点Q，问点P在直线AB的什么位置时，QP=QO？这样的点P有几个？并相应地求出∠OCP的度数。解：∵OQ=OC，OQ=OP
∴∠OQC=∠OCQ，
∠QOP=∠QPO 设∠OCP=x度 , 则有：（2）如果点P在线段OB上，显然有PQ＞OQ，所以点P不可能在线段OB上。（1）如上图,当点P在线段OA上时，∵∠OQC=∠OCP=x,
∴∠QPO= （180－∠OQP）= （180－x)
又∠QPO=∠OCP+∠COP， (180－x)=x+30,
解得x=40, 即∠OCP=40度30°xX+30°x+x+x+30°+30°=180°x=40°xX+30°30°x180-x180-x180-x-30180-x-30+180-x-30+180-x=180
X=100
30°x30-x+30-x=x
X=2030-xx30-xQPOCBA（3）如图，当点Ｐ在的ＯＡ延长线上时，
∵∠OQC=∠OCQ=180－ｘ，
∴∠OPQ= 〔180-（180－x)〕= x.
又∵∠QCO=∠CPO+∠COP，
∴ (180－x)= x+30,
解得x=100 即∠OCP=100度（4）如图当Ｐ在ＯＢ的延长线上时，
∵∠OQC= ∠OCQ=x,∴∠OQC=∠QPO+∠QOP,
∴∠QPO= ∠OQC= x,
又∠COA=∠OCP+∠CPO, 解方程30=x+ x,
得到x=20 即∠OCP=20度OQCPBA1. 如图，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图2所示，则△ABC的面积是（ ）
A、10 B、16 C、18 D、20A2. 如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：
①AD=BE；②PQ∥AE；③AP=BQ；
④DE=DP；⑤∠AOB=60°.
恒成立的结论有_________________（把你认为正确的序号都填上）。 ① ② ③⑤3．一组线段AB和CD把正方形分成形状相同，面积相等的四部分，现给出四种方法，如图所示，请你从中找出线段AB，CD的位置关系： ；线段AB，CD存在的规律：
；
符合这种规律的线段共有无数 组。AB⊥CD 无数 AB和CD经过正方形ABCD的中心且AB⊥CD，AB=CD4．如图1，图2，四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F。
⑴如图1，当点E在AB边的中点位置时：
①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是 ；
②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是 ；
③请证明你的上述两猜想。 图1图2 图2
NE=BF DE=EF⑴③证明：
∵四边形ABCD是正方形，
∴AB=AD,∠A=∠ABC=90°
∴∠MBC=90°∵BF平分∠CBM，∴∠CBF==∠MBF=45°
∴∠DNE==90°+45°=135°
∵N，E分别为AD，AB的中点，
∴DN=EB=AE=AN
∴∠ANE=∠AEN=45°
∴∠EBF=90°+45°=135°∴∠DNE=∠EBF
∵∠NDE+∠DEA=90°，
∠BEF+∠DEA
=180°-∠DEF =180°-90°=90°，
∴∠NDE=∠BEF
∴△DNE≌△EBF
∴ DE=EF，NE=BF
图1⑵如图2，当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。图2 图2⑵在DA边上截取DN=EB
（或截取AN=AE），连结NE，
点N就使得NE=BF成立.
此时，DE=EF。N5．如图，点A在Y轴上，点B在X轴上，且OA=OB=1，经过原点O的直线L交线段AB于点C，过C作OC的垂线，与直线X=1相交于点P，现将直线L绕O点旋转，使交点C从A向B运动，但C点必须在第一象限内，并记AC的长为t，分析此图后，对下列问题作出探究：
（1）通过动手测量线段OC和CP的长来判断它们之间的大小关系？并证明你得到的结论。
（2）当△AOC和△BCP全等时，求出t的值。
（3）①设点P的坐标为（1,b）,试写出b关于t的函数关系式和变量t的取值范围。②求出当△PBC为等腰三角形时点P的坐标。解：（1）OC=CP
证明：过点C作DE⊥OA于D，
交直线BP于点E，
∵直线BE的解析式为X=1，
∴BE⊥OB，∵∠AOB=9O°
∴四边形DOBE为矩形，∴OD=BE，
∵OA=OB，
∴∠ABO=∠OAB=45°∴∠CBE=∠BCE=45°
∴CE=BE∴OD=CE∵OC⊥CP∴∠1+∠2=9O°
∵∠2+∠3=9O°∴∠1=∠3∵∠ODC=∠CEP=9O°
∴△ODC≌△CEP
∴OC=CP（2）当△AOC和△BCP全等时，求出t的值。
（2）∵△AOC≌△BCP
∴OA=BC=1，
∴AB=AC+BC=t+1在Rt△AOB中，
∵∠OAB=45°
∵AB2 =OA2+OB2
∴（t+1）2=12 +12
∴t1= t2=- （舍去）
∴t的值为3）①设点P的坐标为（1,b）,试写出b关于t的函数关系式和变量t的取值范围。
（3）①在Rt△ADC中，∵∠OAB=45°
∴AD=CD，∵AC2 = AD2+CD2
∴2CD2 =t 2∴AD=CD=∴OD=OA-AD=1-
∴BE=OD=1-
在∵△ODC≌△CEP∴CD=PE= ，；
当P在第一象限时BP=BE-PE=1- - =1- t
∵点P的坐标为（1,b）,
∴BP=b∴ （0当P在第四象限时
BP= PE -BE = -1+ =-1+ t
BP=-b
∴ （ ∴b关于t的函数关系式为 （0则PC=PB =1-t
在Rt△PEC中，PC2 =PE2+CE2
∴（1- t）2= （ ）2 +（1- ）2
解得t1= （舍去）t2=0（舍去）
当P在第四象限时只有当BP=BC时,△PBC为等腰三角形
则PB=BC=-b=-1+t
在Rt△PEC中，BC2 =BE2+CE2
∴（-1+ t）2 =（1- ）2+（1- ）2
解得t1=1，t2=0（舍去）
∴ =1- ∴点P的坐标为P（1，1－ ）。