第七章 二项分布与超几何分布的综合应用(含解析)-2024春高中数学选择性必修3(人教版)
文档属性
| 名称 | 第七章 二项分布与超几何分布的综合应用(含解析)-2024春高中数学选择性必修3(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 310.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 13:06:23 | ||
图片预览




文档简介
习题课 二项分布与超几何分布的综合应用
1.某一档深受观众喜爱的电视节目采用组团比赛的方式进行,参赛选手需要全部参加完五场公开比赛,其中五场中有四场获胜,就能取得参加决赛的资格.若某参赛选手每场比赛获胜的概率是,则这名选手能参加决赛的概率是( )
A. B. C. D.
2.PM2.5是指环境空气中空气动力学当量直径小于等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2022年全年每天的PM2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如表所示.
PM2.5日均值(微克/立方米) (25,35] (35,45] (45,55] (55,65] (65,75] (75,85]
频数 3 1 1 1 1 3
从这10天的数据中任取3天数据,记X表示抽到PM2.5监测值超标的天数,则X的均值是( )
A. B. C. D.
3.某同学上学路上要经过3个红绿灯,在每个红绿灯处遇到红灯的概率都是,且在各红绿灯处是否遇到红灯是相互独立的,记X为遇到红灯的次数,若Y=3X+5,则Y的标准差为( )
A. B.3
C. D.2
4.(多选)在一个袋中装有大小一样的6个豆沙粽,4个咸肉粽,现从中任取4个粽子,设取出的4个粽子中咸肉粽的个数为X,则下列结论正确的是( )
A.P(X=2)=
B.E(X)=
C.随机变量X服从超几何分布
D.P(15.从一批含有13件正品,2件次品的产品中不放回地抽3次,每次抽取1件,设抽取的次品数为ξ,则E(5ξ+1)等于( )
A.2 B.1 C.3 D.4
6.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数的概率为( )
A. B. C. D.
7.某校为了解高三学生身体素质情况,从某项体育测试成绩中随机抽取n个学生成绩进行分析,得到成绩频率分布直方图(如图所示).已知成绩在[90,100]的学生人数为8,且有4个女生的成绩在[50,60)中,则n=________,现从成绩在[50,60)的样本中随机抽取2名学生,记所抽取学生中女生的人数为ξ,则ξ的均值是________.
8.某公司有日生产件数为95的“生产能手”3人,有日生产件数为55的“新手”2人,从这5人中任意抽取2人,则2人的日生产件数之和X的标准差为________.
9.某校计划举行知识竞赛,对前来报名者进行初试,初试合格者进入正赛.初试有备选题6道,从备选题中随机挑选出4道题进行测试,至少答对3道题者视为合格.已知甲、乙两人报名参加,在这6道题中甲能答对4道,乙能答对每道题的概率均为,且甲、乙两人各题是否答对相互独立.
(1)分别求甲、乙两人进入正赛的概率;
(2)记甲、乙两人中进入正赛的人数为ξ,求ξ的分布列及E(2ξ-1).
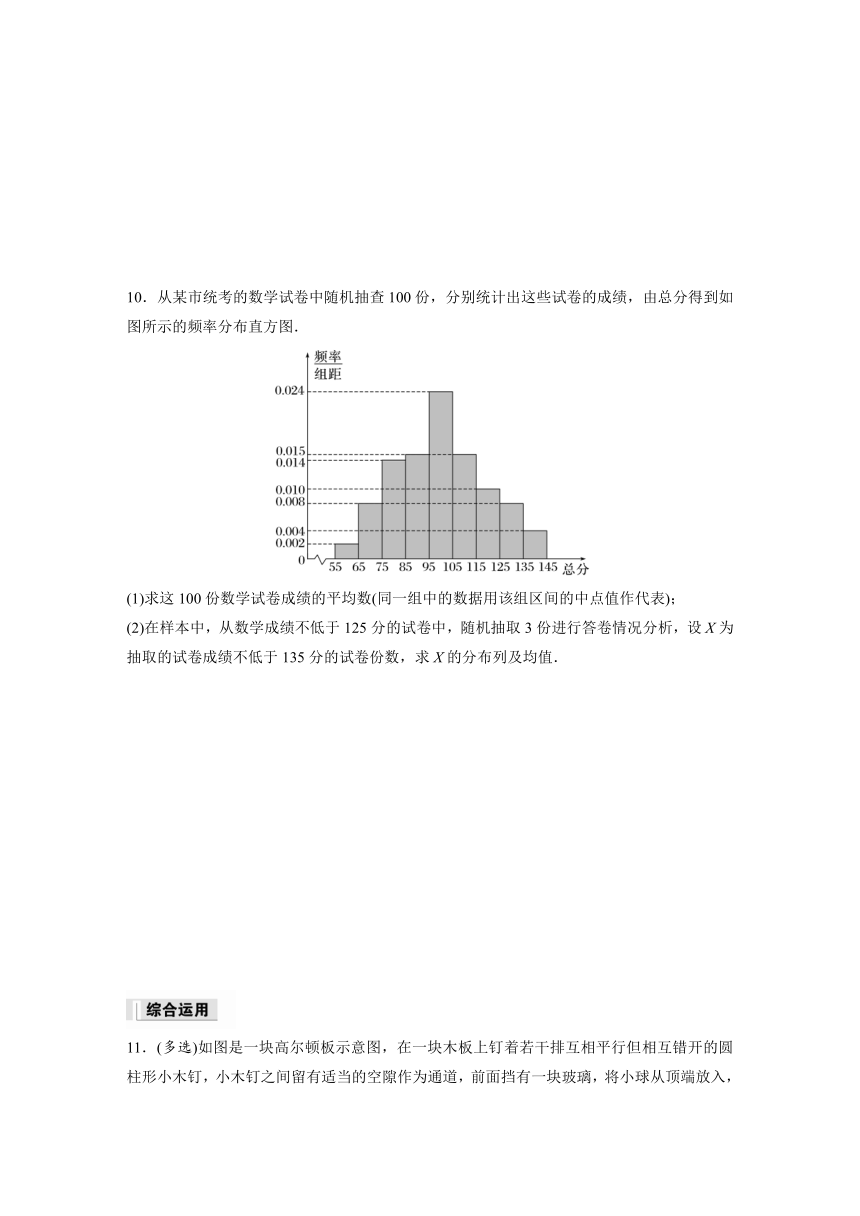
10.从某市统考的数学试卷中随机抽查100份,分别统计出这些试卷的成绩,由总分得到如图所示的频率分布直方图.
(1)求这100份数学试卷成绩的平均数(同一组中的数据用该组区间的中点值作代表);
(2)在样本中,从数学成绩不低于125分的试卷中,随机抽取3份进行答卷情况分析,设X为抽取的试卷成绩不低于135分的试卷份数,求X的分布列及均值.
11.(多选)如图是一块高尔顿板示意图,在一块木板上钉着若干排互相平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃,将小球从顶端放入,小球在下落过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中,格子从左到右分别编号为0,1,2,3,…,10,用X表示小球落入格子的号码,则( )
A.P(X=1)=P(X=9)=
B.P(X=1)=P(X=9)=
C.E(X)=10
D.D(X)=
12.为了防止受到核污染的产品影响我国民众的身体健康,有关部门要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响,若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)等于( )
A. B. C. D.
13.口袋中有相同的黑色小球n个,红、白、蓝色的小球各一个,从中任取4个小球.ξ表示当n=3时取出黑球的数目,η表示当n=4时取出黑球的数目.则下列结论成立的是( )
A.E(ξ)<E(η),D(ξ)<D(η)
B.E(ξ)>E(η),D(ξ)<D(η)
C.E(ξ)<E(η),D(ξ)>D(η)
D.E(ξ)>E(η),D(ξ)>D(η)
14.为了降低对大气污染和能源消耗,某品牌汽车制造商研发了两款电动汽车(车型A和车型B),并在“十一黄金周”期间同时投放市场.为了了解这两款车型在“十一黄金周”的销售情况,制造商随机调查了5家汽车4S店的销量(单位:台),得到如下数据:
4S店 车型 甲 乙 丙 丁 戊
车型A 6 6 13 8 11
车型B 12 9 13 6 4
现从这5家汽车4S店中任选3家举行促销活动,用X表示其中车型A销量超过车型B销量的4S店的个数,则D(X)=________.
15.如果一个数含有正偶数个数字8,就称它为“优选数”(如188,38 888等),否则就称它为“非优选数”,从由数字0,1,2,…,9共10个数字组成的四位数中任意抽取10个数,用随机变量X表示抽到的“优选数”的个数,则E(X)=________.
16.幸福农场生产的某批次的20件产品中含有n件次品,从中一次任取10件,其中次品恰有X件.
(1)若n=3,求取出的产品中次品不超过1件的概率;
(2)记f(n)=P(X=3),则当n为何值时,f(n)取得最大值.
习题课 二项分布与超几何分布的综合应用
1.D [由题意可知五场中获胜的场次X~B, 所以所求选手能参加决赛的概率P=C×4×+C×5×0=.]
2.A [由题意知,X服从超几何分布,其中N=10,M=3,n=3,所以E(X)===.]
3.A [因为该同学经过每个红绿灯时是否遇到红灯互不影响,所以可看成3重伯努利试验,
即X~B,
则X的方差D(X)
=3××=,
所以Y的方差D(Y)=32·D(X)=9×=6,
所以Y的标准差为=.]
4.ACD [由题意知,随机变量X服从参数为10,4,4的超几何分布,
则E(X)==,所以B错误,C正确;
又P(X=2)==,
P(X=3)==,
所以P(1=P(X=2)+P(X=3)=+=,
所以A,D正确.]
5.C [ξ的可能取值为0,1,2.
P(ξ=0)==,
P(ξ=1)==,
P(ξ=2)==.
所以ξ的分布列为
ξ 0 1 2
P
于是E(ξ)=0×+1×+2×=,
故E(5ξ+1)=5E(ξ)+1=5×+1=3.]
6.C [由题意可知,10个数中,1,3,5,7,9是阳数,2,4,6,8,10是阴数,
若任取3个数中有2个阳数,
则P===,
若任取3个数中有3个阳数,
则P===,
故这3个数中至少有2个阳数的概率P=+=.]
7.50
解析 依题意得0.016×10n=8,
则n=50.
成绩在[50,60)的人数为0.012×10×50=6,
其中4个为女生,2个为男生.
ξ的可能取值为0,1,2.
P(ξ=0)==,
P(ξ=1)==,
P(ξ=2)==,
故E(ξ)=0×+1×+2×
=.
8.24
解析 由题意,可得X的所有可能取值为190,150,110,且P(X=190)==,P(X=150)==,P(X=110)==,则E(X)=190×+150×+110×=158,标准差为==24.
9.解 (1)设甲、乙两人答对的题目数分别为X,Y,则Y~B,
可得甲进入正赛的概率
P1==,
乙进入正赛的概率P2=P(Y=3)+P(Y=4)=C×3×+C×4=,
故甲、乙两人进入正赛的概率分别为,.
(2)由题意可得,ξ的可能取值为0,1,2,则有
P(ξ=0)=(1-P1)(1-P2)
=×=,
P(ξ=1)=P1(1-P2)+(1-P1)P2=×+×=,
P(ξ=2)=P1P2=×=,
则ξ的分布列为
ξ 0 1 2
P
则E(ξ)=0×+1×+2×
=,
故E(2ξ-1)=2E(ξ)-1=.
10.解 (1)这100份数学试卷成绩的平均数为
60×0.02+70×0.08+80×0.14+90×0.15+100×0.24+110×0.15+120×0.1+130×0.08+140×0.04=100.
(2)抽查的100份试卷中,成绩位于区间[125,135)的有8份,
位于区间的有4份,共计12份试卷.
从中抽取3份试卷,这3份试卷中成绩在的试卷份数X的可能取值是0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
则X的分布列为
X 0 1 2 3
P
X的均值为E(X)=0×+1×+2×+3×==1.
11.AD [设A=“向右下落”,=“向左下落”,则P(A)=P()=,
因为小球最后落入格子的号码X等于事件A发生的次数,而小球下落的过程中共碰撞小木钉10次,
所以X~B,于是P(X=1)=C××9=,
同理可得,P(X=9)=C×9×=,A正确,B错误;由二项分布求均值及方差公式得,E(X)=10×=5,D(X)=10××=,C错误,D正确.]
12.B [由题意得该产品能销售的概率为×=,
易知X的所有可能取值为-320,-200,-80,40,160,
设ξ表示一箱产品中可以销售的件数,则ξ~B,所以P(ξ=k)=C×k×4-k,k=0,1,2,3,4.
所以P(X=-80)=P(ξ=2)=C×2×2=,P(X=40)=P(ξ=3)=C×3×1=,P(X=160)=P(ξ=4)=C×4×0=,
故P(X≥-80)=P(X=-80)+P(X=40)+P(X=160)
=++=.]
13.A [当n=3时,ξ的可能取值为1,2,3,
P(ξ=1)==,
P(ξ=2)==,
P(ξ=3)==,
∴E(ξ)=1×+2×+3×=2,
D(ξ)=(1-2)2×+(2-2)2×+(3-2)2×=.
当n=4时,η的可能取值为1,2,3,4,
P(η=1)==,
P(η=2)==,
P(η=3)==,
P(η=4)==,
∴E(η)=1×+2×+3×+4×=,
D(η)=2×+2×+2×+2×=.
∴E(ξ)14.
解析 由表可知,车型A销量超过车型B销量的4S店有2家,则X的所有可能取值为0,1,2,
且P(X=0)==,
P(X=1)==,
P(X=2)==,
所以E(X)=0×+1×+2×=,
D(X)=2×+2×+2×=.
15.
解析 当四位数中含有两个8时,若8不在首位,共有C×8×9=216(个),若8在首位,共有C×9×9=243(个);当四位数中含有四个8时,只有一种结果,所以从由数字0,1,2,…,9组成的四位数中,“优选数”共有460个,X的可能取值为0,1,2,…,9,10,已知随机变量X服从超几何分布,其中n=10,M=460,N=9 000,故E(X)=== .
16.解 (1)记“取出的产品中次品不超过1件”为事件A,
则P(A)=P(X=0)+P(X=1).
因为P(X=0)==,
P(X=1)==,
所以P(A)=+=.
则取出的产品中次品不超过1件的概率是.
(2)因为f(n)=P(X=3)=,
则f(n+1)=.
由=
=>1,解得n<.
因为n∈N*,则n≤5,
故当3≤n≤5时,>1;
当6≤n≤13时,<1;
所以当n=6时,f(n)取得最大值.
1.某一档深受观众喜爱的电视节目采用组团比赛的方式进行,参赛选手需要全部参加完五场公开比赛,其中五场中有四场获胜,就能取得参加决赛的资格.若某参赛选手每场比赛获胜的概率是,则这名选手能参加决赛的概率是( )
A. B. C. D.
2.PM2.5是指环境空气中空气动力学当量直径小于等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2022年全年每天的PM2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如表所示.
PM2.5日均值(微克/立方米) (25,35] (35,45] (45,55] (55,65] (65,75] (75,85]
频数 3 1 1 1 1 3
从这10天的数据中任取3天数据,记X表示抽到PM2.5监测值超标的天数,则X的均值是( )
A. B. C. D.
3.某同学上学路上要经过3个红绿灯,在每个红绿灯处遇到红灯的概率都是,且在各红绿灯处是否遇到红灯是相互独立的,记X为遇到红灯的次数,若Y=3X+5,则Y的标准差为( )
A. B.3
C. D.2
4.(多选)在一个袋中装有大小一样的6个豆沙粽,4个咸肉粽,现从中任取4个粽子,设取出的4个粽子中咸肉粽的个数为X,则下列结论正确的是( )
A.P(X=2)=
B.E(X)=
C.随机变量X服从超几何分布
D.P(1
A.2 B.1 C.3 D.4
6.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数的概率为( )
A. B. C. D.
7.某校为了解高三学生身体素质情况,从某项体育测试成绩中随机抽取n个学生成绩进行分析,得到成绩频率分布直方图(如图所示).已知成绩在[90,100]的学生人数为8,且有4个女生的成绩在[50,60)中,则n=________,现从成绩在[50,60)的样本中随机抽取2名学生,记所抽取学生中女生的人数为ξ,则ξ的均值是________.
8.某公司有日生产件数为95的“生产能手”3人,有日生产件数为55的“新手”2人,从这5人中任意抽取2人,则2人的日生产件数之和X的标准差为________.
9.某校计划举行知识竞赛,对前来报名者进行初试,初试合格者进入正赛.初试有备选题6道,从备选题中随机挑选出4道题进行测试,至少答对3道题者视为合格.已知甲、乙两人报名参加,在这6道题中甲能答对4道,乙能答对每道题的概率均为,且甲、乙两人各题是否答对相互独立.
(1)分别求甲、乙两人进入正赛的概率;
(2)记甲、乙两人中进入正赛的人数为ξ,求ξ的分布列及E(2ξ-1).
10.从某市统考的数学试卷中随机抽查100份,分别统计出这些试卷的成绩,由总分得到如图所示的频率分布直方图.
(1)求这100份数学试卷成绩的平均数(同一组中的数据用该组区间的中点值作代表);
(2)在样本中,从数学成绩不低于125分的试卷中,随机抽取3份进行答卷情况分析,设X为抽取的试卷成绩不低于135分的试卷份数,求X的分布列及均值.
11.(多选)如图是一块高尔顿板示意图,在一块木板上钉着若干排互相平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃,将小球从顶端放入,小球在下落过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中,格子从左到右分别编号为0,1,2,3,…,10,用X表示小球落入格子的号码,则( )
A.P(X=1)=P(X=9)=
B.P(X=1)=P(X=9)=
C.E(X)=10
D.D(X)=
12.为了防止受到核污染的产品影响我国民众的身体健康,有关部门要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响,若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)等于( )
A. B. C. D.
13.口袋中有相同的黑色小球n个,红、白、蓝色的小球各一个,从中任取4个小球.ξ表示当n=3时取出黑球的数目,η表示当n=4时取出黑球的数目.则下列结论成立的是( )
A.E(ξ)<E(η),D(ξ)<D(η)
B.E(ξ)>E(η),D(ξ)<D(η)
C.E(ξ)<E(η),D(ξ)>D(η)
D.E(ξ)>E(η),D(ξ)>D(η)
14.为了降低对大气污染和能源消耗,某品牌汽车制造商研发了两款电动汽车(车型A和车型B),并在“十一黄金周”期间同时投放市场.为了了解这两款车型在“十一黄金周”的销售情况,制造商随机调查了5家汽车4S店的销量(单位:台),得到如下数据:
4S店 车型 甲 乙 丙 丁 戊
车型A 6 6 13 8 11
车型B 12 9 13 6 4
现从这5家汽车4S店中任选3家举行促销活动,用X表示其中车型A销量超过车型B销量的4S店的个数,则D(X)=________.
15.如果一个数含有正偶数个数字8,就称它为“优选数”(如188,38 888等),否则就称它为“非优选数”,从由数字0,1,2,…,9共10个数字组成的四位数中任意抽取10个数,用随机变量X表示抽到的“优选数”的个数,则E(X)=________.
16.幸福农场生产的某批次的20件产品中含有n件次品,从中一次任取10件,其中次品恰有X件.
(1)若n=3,求取出的产品中次品不超过1件的概率;
(2)记f(n)=P(X=3),则当n为何值时,f(n)取得最大值.
习题课 二项分布与超几何分布的综合应用
1.D [由题意可知五场中获胜的场次X~B, 所以所求选手能参加决赛的概率P=C×4×+C×5×0=.]
2.A [由题意知,X服从超几何分布,其中N=10,M=3,n=3,所以E(X)===.]
3.A [因为该同学经过每个红绿灯时是否遇到红灯互不影响,所以可看成3重伯努利试验,
即X~B,
则X的方差D(X)
=3××=,
所以Y的方差D(Y)=32·D(X)=9×=6,
所以Y的标准差为=.]
4.ACD [由题意知,随机变量X服从参数为10,4,4的超几何分布,
则E(X)==,所以B错误,C正确;
又P(X=2)==,
P(X=3)==,
所以P(1
所以A,D正确.]
5.C [ξ的可能取值为0,1,2.
P(ξ=0)==,
P(ξ=1)==,
P(ξ=2)==.
所以ξ的分布列为
ξ 0 1 2
P
于是E(ξ)=0×+1×+2×=,
故E(5ξ+1)=5E(ξ)+1=5×+1=3.]
6.C [由题意可知,10个数中,1,3,5,7,9是阳数,2,4,6,8,10是阴数,
若任取3个数中有2个阳数,
则P===,
若任取3个数中有3个阳数,
则P===,
故这3个数中至少有2个阳数的概率P=+=.]
7.50
解析 依题意得0.016×10n=8,
则n=50.
成绩在[50,60)的人数为0.012×10×50=6,
其中4个为女生,2个为男生.
ξ的可能取值为0,1,2.
P(ξ=0)==,
P(ξ=1)==,
P(ξ=2)==,
故E(ξ)=0×+1×+2×
=.
8.24
解析 由题意,可得X的所有可能取值为190,150,110,且P(X=190)==,P(X=150)==,P(X=110)==,则E(X)=190×+150×+110×=158,标准差为==24.
9.解 (1)设甲、乙两人答对的题目数分别为X,Y,则Y~B,
可得甲进入正赛的概率
P1==,
乙进入正赛的概率P2=P(Y=3)+P(Y=4)=C×3×+C×4=,
故甲、乙两人进入正赛的概率分别为,.
(2)由题意可得,ξ的可能取值为0,1,2,则有
P(ξ=0)=(1-P1)(1-P2)
=×=,
P(ξ=1)=P1(1-P2)+(1-P1)P2=×+×=,
P(ξ=2)=P1P2=×=,
则ξ的分布列为
ξ 0 1 2
P
则E(ξ)=0×+1×+2×
=,
故E(2ξ-1)=2E(ξ)-1=.
10.解 (1)这100份数学试卷成绩的平均数为
60×0.02+70×0.08+80×0.14+90×0.15+100×0.24+110×0.15+120×0.1+130×0.08+140×0.04=100.
(2)抽查的100份试卷中,成绩位于区间[125,135)的有8份,
位于区间的有4份,共计12份试卷.
从中抽取3份试卷,这3份试卷中成绩在的试卷份数X的可能取值是0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
则X的分布列为
X 0 1 2 3
P
X的均值为E(X)=0×+1×+2×+3×==1.
11.AD [设A=“向右下落”,=“向左下落”,则P(A)=P()=,
因为小球最后落入格子的号码X等于事件A发生的次数,而小球下落的过程中共碰撞小木钉10次,
所以X~B,于是P(X=1)=C××9=,
同理可得,P(X=9)=C×9×=,A正确,B错误;由二项分布求均值及方差公式得,E(X)=10×=5,D(X)=10××=,C错误,D正确.]
12.B [由题意得该产品能销售的概率为×=,
易知X的所有可能取值为-320,-200,-80,40,160,
设ξ表示一箱产品中可以销售的件数,则ξ~B,所以P(ξ=k)=C×k×4-k,k=0,1,2,3,4.
所以P(X=-80)=P(ξ=2)=C×2×2=,P(X=40)=P(ξ=3)=C×3×1=,P(X=160)=P(ξ=4)=C×4×0=,
故P(X≥-80)=P(X=-80)+P(X=40)+P(X=160)
=++=.]
13.A [当n=3时,ξ的可能取值为1,2,3,
P(ξ=1)==,
P(ξ=2)==,
P(ξ=3)==,
∴E(ξ)=1×+2×+3×=2,
D(ξ)=(1-2)2×+(2-2)2×+(3-2)2×=.
当n=4时,η的可能取值为1,2,3,4,
P(η=1)==,
P(η=2)==,
P(η=3)==,
P(η=4)==,
∴E(η)=1×+2×+3×+4×=,
D(η)=2×+2×+2×+2×=.
∴E(ξ)
解析 由表可知,车型A销量超过车型B销量的4S店有2家,则X的所有可能取值为0,1,2,
且P(X=0)==,
P(X=1)==,
P(X=2)==,
所以E(X)=0×+1×+2×=,
D(X)=2×+2×+2×=.
15.
解析 当四位数中含有两个8时,若8不在首位,共有C×8×9=216(个),若8在首位,共有C×9×9=243(个);当四位数中含有四个8时,只有一种结果,所以从由数字0,1,2,…,9组成的四位数中,“优选数”共有460个,X的可能取值为0,1,2,…,9,10,已知随机变量X服从超几何分布,其中n=10,M=460,N=9 000,故E(X)=== .
16.解 (1)记“取出的产品中次品不超过1件”为事件A,
则P(A)=P(X=0)+P(X=1).
因为P(X=0)==,
P(X=1)==,
所以P(A)=+=.
则取出的产品中次品不超过1件的概率是.
(2)因为f(n)=P(X=3)=,
则f(n+1)=.
由=
=>1,解得n<.
因为n∈N*,则n≤5,
故当3≤n≤5时,>1;
当6≤n≤13时,<1;
所以当n=6时,f(n)取得最大值.
