辽宁省盘锦市育才中学2023-2024学年九年级下学期期初考试数学试卷(无答案)
文档属性
| 名称 | 辽宁省盘锦市育才中学2023-2024学年九年级下学期期初考试数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 708.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 12:31:06 | ||
图片预览


文档简介
盘锦育才学校2023—2024学年度下学期初三第一次模
数学模报试题
时间:120分钟 满分:120分
一、选择题(每小题3分。共计30分)
1.七年级(1)班期未考试数学的平均成缓是83分,小亮得了90分,+7分,小英的成绩记作-3分,表示得了( )分.
A.85 B.83 C.87 D.80
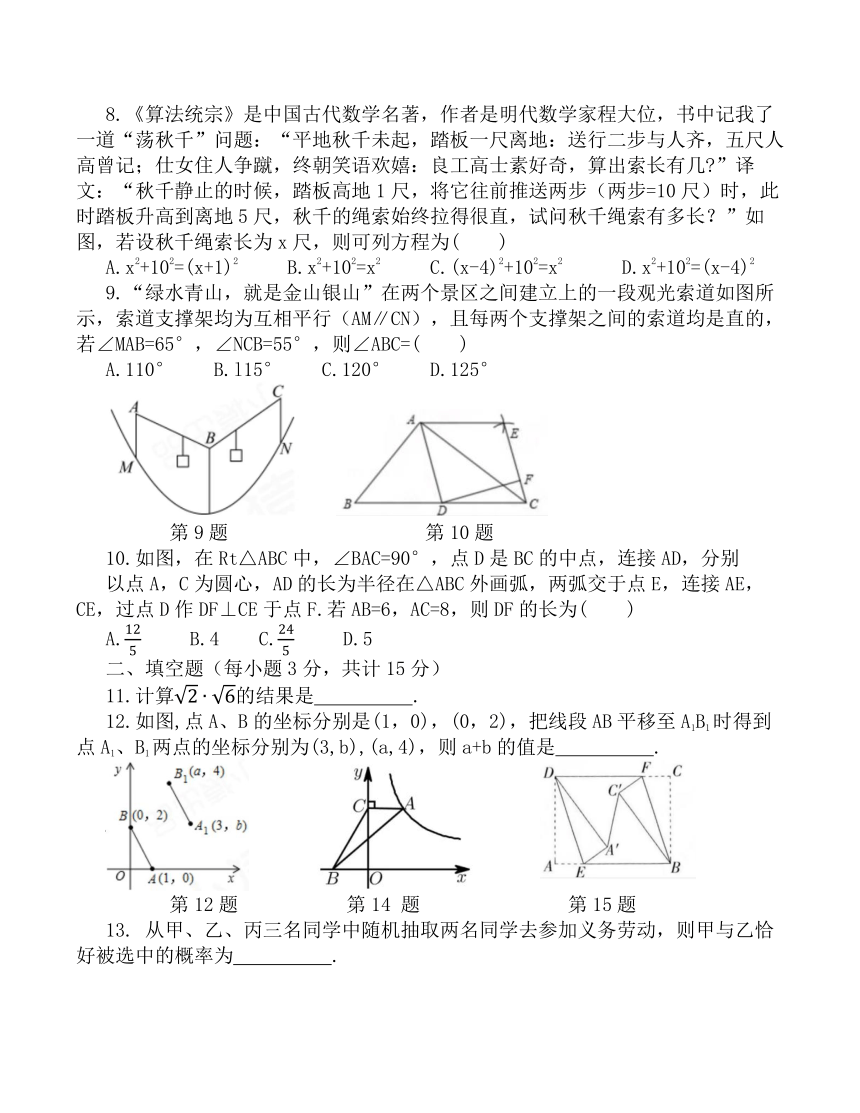
2.如下图所示的立体图形的视图是( )
3.下列图案中,既是轴对称图形又是中心对称图形的是( )
4.下列运算正确的是( )
A.a2.a3=a6 B. C.a4÷a=a3 D.2a+3a=5a2
5.若关于x的一元二次方程kx2-6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k1 C.k<1且k≠0 D.k1且k≠0
6.把分式方程转化为一元一次方程时,方程两边需同乘以( )
A.x-1 B.x+1 C.x2-1 D.x2-x
7.如图是一次函数y1=kx+b与y2=x+a的图象,则下列结论:①k<0:②a>0:③b>0:④方程kx+b=x+a的解是x=3.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
第7题图 第8题图
8.《算法统宗》是中国古代数学名著,作者是明代数学家程大位,书中记我了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地:送行二步与人齐,五尺人高曾记;仕女住人争蹴,终朝笑语欢嬉:良工高士素好奇,算出索长有几 ”译文:“秋千静止的时候,踏板高地1尺,将它往前推送两步(两步=10尺)时,此时踏板升高到离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长?”如图,若设秋千绳索长为x尺,则可列方程为( )
A.x2+102=(x+1)2 B.x2+102=x2 C.(x-4)2+102=x2 D.x2+102=(x-4)2
9.“绿水青山,就是金山银山”在两个景区之间建立上的一段观光索道如图所示,索道支撑架均为互相平行(AM∥CN),且每两个支撑架之间的索道均是直的,若∠MAB=65°,∠NCB=55°,则∠ABC=( )
A.110° B.l15° C.120° D.125°
第9题 第10题
10.如图,在Rt△ABC中,∠BAC=90°,点D是BC的中点,连接AD,分别
以点A,C为圆心,AD的长为半径在△ABC外画弧,两弧交于点E,连接AE,CE,过点D作DF⊥CE于点F.若AB=6,AC=8,则DF的长为( )
A. B.4 C. D.5
二、填空题(每小题3分,共计15分)
11.计算的结果是 .
12.如图,点A、B的坐标分别是(1,0),(0,2),把线段AB平移至A1B1时得到点A1、B1两点的坐标分别为(3,b),(a,4),则a+b的值是 .
第12题 第14 题 第15题
13. 从甲、乙、丙三名同学中随机抽取两名同学去参加义务劳动,则甲与乙恰好被选中的概率为 .
14.如图,在平面直角坐标系中,点A在函数y=(r>0)的图像上,过点A作AC⊥y轴于点C,点B在x轴上,连接CB、AB,若△ABC的面积为3,则k的值为 .
15.如图,四边形ABCD为矩形,AB=8,AD=6,点E,F分别为边AB,CD上动点,且AE=CF,连接DE,BF,分别将△DAE和△BCF沿DE,BF翻折,点A的对应点为点A′,点C的对应点为点C′,连接A′C′,当点A′,C′均落在矩形ABCD的同一条对角线上时,AE长为 .
三、解答题(共75分)
16.计算(每小题5分,共10分)
(1)计算:
(2)化简:
17.一方有难,八方支援。“新冠肺炎”疫情来袭,除了医务人员主动请缨
逆行走向战场外,众多企业也伸出援助之手,某公司用甲,乙两种货车向疫
区运送爱心物资,两次满载的运输情况如表:
甲种货车辆数 乙种货车辆数 合计运物资吨数
第一次 2 3 22
第二次 4 5 40
(1)求甲,乙两种货车每次满载分别能运输多少吨物资;
(2)由于疫情的持续,该公司安排甲、乙货车共10辆进行第三次物资的运送,运送的物资不少于47.4吨,请向该公司应至少安排甲种货车多少辆?
18.(9分),为庆祝中国共产党成立102周年,某中学举行党史知识竞赛。团委随机抽取了部分学生的成绩作为样本,把成绩得分x(满分100分)按四个等级分别进行统计,并将所得数据绘制成如下不完整的统计图。
请根据图中提供的信息,解答下列问题:
(1)本次抽查的学生人数是 人;
(2)补全条形统计图,并指出成绩的中位数落在哪个等级:
(3)学校计划给参加党史竞赛获得良好、优秀两个等级的同学每人分别奖励价值3元、5元的学习用品,该校共有1000名学生参加党史竞赛,试估计此次竞赛该校用于奖励学生的费用
19.(8分)某企业接到一批服装生产任务, 要求15天完成,为按时完成任务,若干天后,该企业增加了一定数目的生产工人,该企业能x天累计生产服装的数量为y件。y与x之间的关系如图所示.
(1)这批服装一共有 件,写出点A的实际意义 ;
(2)求增加工人后y与x的函数表达式;
(3)已知这批服装的出厂价为每件80元,由于特殊原因,原材料紧缺,服装的成本前5天为每件50元,从第6天起每件的成本比原先增加了10元,问前几天的总利润恰好为9600元(利润=出厂价一成本)
20.(8分)如图,无人机爱好者小明在家附近放无人机,当无人机飞行到小明头项一定高度D点处时,无人机测得楼房BC顶端点C处的俯角为30°,已知小明A和小区楼房BC之间的距离为36米,楼房BC的高度为12米.
(1)求此时无人机离地面的高度;
(2)在(1)条件下,若无人机保持现有高度沿平行于AB的方向,并以4米/秒的速度继续向前匀速飞行,问:经过多少秒时,无人机刚好离开了小明的视线?(假定点A,B. C,D都在同一平面内)
21.如图△ABC中,AB=BC,以AC为直径的⊙0分别交边AB,BC于点D,E,过点A作⊙O的切线交CB的延长线于点F.
(1)求证:AB=BF;
(2)若AF=8,cos∠BAF= ,求BC和DE的长.
22.(12分)[生活情境]为美化校园环境,某学校根据地形情况,要对景观带中一个长AD=4m,宽AB=1m的长方形水池ABCD进行加长改造(如图①.改造后的水池ABNM仍为长方形,以下简称水池1),同时,再建造一个周长为12m的矩形水池EFGH(如图2,以下简称水池2).
[建立摸型]
如果设水池ABCD的边AD加长长度DM为x(m)(x>O),加长后水池1的总面积为y1(m2),则y1关于x的函数解析式为:y1=x+4(x>0):设水池2的边EF的长为x(m)(O[问题解决]
(1)若水池2的面积随EF长度的增加而减小,则EF长度的取值范围
是 (可省略单位),水池2面积的最大值是 m2;
(2)在图3字母标注的点中,表示两个水池面积相等的点是 ,此时的
x(m)值是 .
(3)当水池1的面积大于水池2的面积时,x(m)的取值范围是 .
(4)在1(5)假设水池ABCD的边AD的长度为b(m),其他条件不变(这个加长改造后的新水池简称水池3),则水池3的总面积y3(m2)关于x(m)(x>0)的函数解析式为:y3=x+b(x>0).若水池3与水池2的面积相等时,x(m)有唯一值,求b的值.
23.(12分)在Rt△ABC中,∠ACB=90°,CA=CB,点0为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.
(1)如图1,当点D与点0重合时,请直接写出线段AD与线段EF的数量关系;
(2)如图2,当点D在线段AB上时,求证:CG+BD=BC;
(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3
时,请直接写出的值.
数学模报试题
时间:120分钟 满分:120分
一、选择题(每小题3分。共计30分)
1.七年级(1)班期未考试数学的平均成缓是83分,小亮得了90分,+7分,小英的成绩记作-3分,表示得了( )分.
A.85 B.83 C.87 D.80
2.如下图所示的立体图形的视图是( )
3.下列图案中,既是轴对称图形又是中心对称图形的是( )
4.下列运算正确的是( )
A.a2.a3=a6 B. C.a4÷a=a3 D.2a+3a=5a2
5.若关于x的一元二次方程kx2-6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k1 C.k<1且k≠0 D.k1且k≠0
6.把分式方程转化为一元一次方程时,方程两边需同乘以( )
A.x-1 B.x+1 C.x2-1 D.x2-x
7.如图是一次函数y1=kx+b与y2=x+a的图象,则下列结论:①k<0:②a>0:③b>0:④方程kx+b=x+a的解是x=3.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
第7题图 第8题图
8.《算法统宗》是中国古代数学名著,作者是明代数学家程大位,书中记我了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地:送行二步与人齐,五尺人高曾记;仕女住人争蹴,终朝笑语欢嬉:良工高士素好奇,算出索长有几 ”译文:“秋千静止的时候,踏板高地1尺,将它往前推送两步(两步=10尺)时,此时踏板升高到离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长?”如图,若设秋千绳索长为x尺,则可列方程为( )
A.x2+102=(x+1)2 B.x2+102=x2 C.(x-4)2+102=x2 D.x2+102=(x-4)2
9.“绿水青山,就是金山银山”在两个景区之间建立上的一段观光索道如图所示,索道支撑架均为互相平行(AM∥CN),且每两个支撑架之间的索道均是直的,若∠MAB=65°,∠NCB=55°,则∠ABC=( )
A.110° B.l15° C.120° D.125°
第9题 第10题
10.如图,在Rt△ABC中,∠BAC=90°,点D是BC的中点,连接AD,分别
以点A,C为圆心,AD的长为半径在△ABC外画弧,两弧交于点E,连接AE,CE,过点D作DF⊥CE于点F.若AB=6,AC=8,则DF的长为( )
A. B.4 C. D.5
二、填空题(每小题3分,共计15分)
11.计算的结果是 .
12.如图,点A、B的坐标分别是(1,0),(0,2),把线段AB平移至A1B1时得到点A1、B1两点的坐标分别为(3,b),(a,4),则a+b的值是 .
第12题 第14 题 第15题
13. 从甲、乙、丙三名同学中随机抽取两名同学去参加义务劳动,则甲与乙恰好被选中的概率为 .
14.如图,在平面直角坐标系中,点A在函数y=(r>0)的图像上,过点A作AC⊥y轴于点C,点B在x轴上,连接CB、AB,若△ABC的面积为3,则k的值为 .
15.如图,四边形ABCD为矩形,AB=8,AD=6,点E,F分别为边AB,CD上动点,且AE=CF,连接DE,BF,分别将△DAE和△BCF沿DE,BF翻折,点A的对应点为点A′,点C的对应点为点C′,连接A′C′,当点A′,C′均落在矩形ABCD的同一条对角线上时,AE长为 .
三、解答题(共75分)
16.计算(每小题5分,共10分)
(1)计算:
(2)化简:
17.一方有难,八方支援。“新冠肺炎”疫情来袭,除了医务人员主动请缨
逆行走向战场外,众多企业也伸出援助之手,某公司用甲,乙两种货车向疫
区运送爱心物资,两次满载的运输情况如表:
甲种货车辆数 乙种货车辆数 合计运物资吨数
第一次 2 3 22
第二次 4 5 40
(1)求甲,乙两种货车每次满载分别能运输多少吨物资;
(2)由于疫情的持续,该公司安排甲、乙货车共10辆进行第三次物资的运送,运送的物资不少于47.4吨,请向该公司应至少安排甲种货车多少辆?
18.(9分),为庆祝中国共产党成立102周年,某中学举行党史知识竞赛。团委随机抽取了部分学生的成绩作为样本,把成绩得分x(满分100分)按四个等级分别进行统计,并将所得数据绘制成如下不完整的统计图。
请根据图中提供的信息,解答下列问题:
(1)本次抽查的学生人数是 人;
(2)补全条形统计图,并指出成绩的中位数落在哪个等级:
(3)学校计划给参加党史竞赛获得良好、优秀两个等级的同学每人分别奖励价值3元、5元的学习用品,该校共有1000名学生参加党史竞赛,试估计此次竞赛该校用于奖励学生的费用
19.(8分)某企业接到一批服装生产任务, 要求15天完成,为按时完成任务,若干天后,该企业增加了一定数目的生产工人,该企业能x天累计生产服装的数量为y件。y与x之间的关系如图所示.
(1)这批服装一共有 件,写出点A的实际意义 ;
(2)求增加工人后y与x的函数表达式;
(3)已知这批服装的出厂价为每件80元,由于特殊原因,原材料紧缺,服装的成本前5天为每件50元,从第6天起每件的成本比原先增加了10元,问前几天的总利润恰好为9600元(利润=出厂价一成本)
20.(8分)如图,无人机爱好者小明在家附近放无人机,当无人机飞行到小明头项一定高度D点处时,无人机测得楼房BC顶端点C处的俯角为30°,已知小明A和小区楼房BC之间的距离为36米,楼房BC的高度为12米.
(1)求此时无人机离地面的高度;
(2)在(1)条件下,若无人机保持现有高度沿平行于AB的方向,并以4米/秒的速度继续向前匀速飞行,问:经过多少秒时,无人机刚好离开了小明的视线?(假定点A,B. C,D都在同一平面内)
21.如图△ABC中,AB=BC,以AC为直径的⊙0分别交边AB,BC于点D,E,过点A作⊙O的切线交CB的延长线于点F.
(1)求证:AB=BF;
(2)若AF=8,cos∠BAF= ,求BC和DE的长.
22.(12分)[生活情境]为美化校园环境,某学校根据地形情况,要对景观带中一个长AD=4m,宽AB=1m的长方形水池ABCD进行加长改造(如图①.改造后的水池ABNM仍为长方形,以下简称水池1),同时,再建造一个周长为12m的矩形水池EFGH(如图2,以下简称水池2).
[建立摸型]
如果设水池ABCD的边AD加长长度DM为x(m)(x>O),加长后水池1的总面积为y1(m2),则y1关于x的函数解析式为:y1=x+4(x>0):设水池2的边EF的长为x(m)(O
(1)若水池2的面积随EF长度的增加而减小,则EF长度的取值范围
是 (可省略单位),水池2面积的最大值是 m2;
(2)在图3字母标注的点中,表示两个水池面积相等的点是 ,此时的
x(m)值是 .
(3)当水池1的面积大于水池2的面积时,x(m)的取值范围是 .
(4)在1
23.(12分)在Rt△ABC中,∠ACB=90°,CA=CB,点0为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.
(1)如图1,当点D与点0重合时,请直接写出线段AD与线段EF的数量关系;
(2)如图2,当点D在线段AB上时,求证:CG+BD=BC;
(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3
时,请直接写出的值.
同课章节目录
