数学人教A版(2019)选择性必修三册7.1.1条件概率 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修三册7.1.1条件概率 课件(共20张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 14:08:51 | ||
图片预览





文档简介
(共20张PPT)
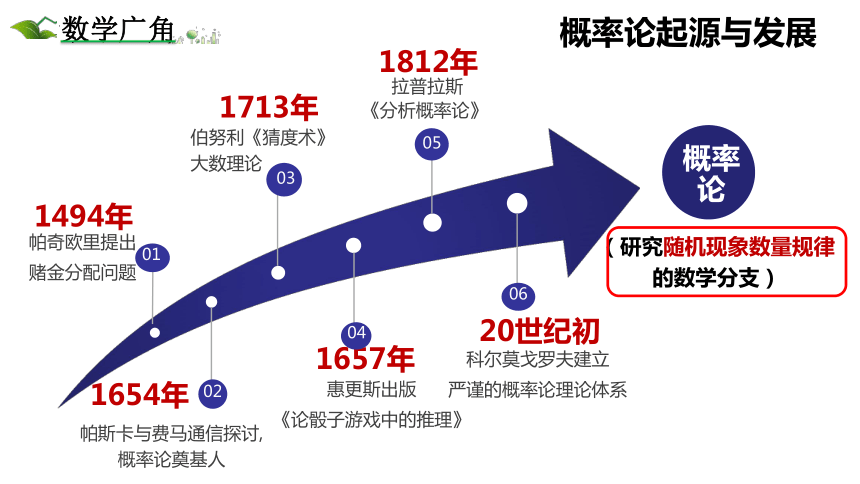
1494年
帕奇欧里提出
赌金分配问题
1654年
帕斯卡与费马通信探讨,概率论奠基人
1657年
惠更斯出版
《论骰子游戏中的推理》
20世纪初
科尔莫戈罗夫建立
严谨的概率论理论体系
01
概率论
1713年
伯努利《猜度术》 大数理论
1812年
拉普拉斯
《分析概率论》
概率论起源与发展
03
05
02
04
06
(研究随机现象数量规律的数学分支)
数学广角
互斥
互为对立
新的概率模型
和事件
积事件
情境一:
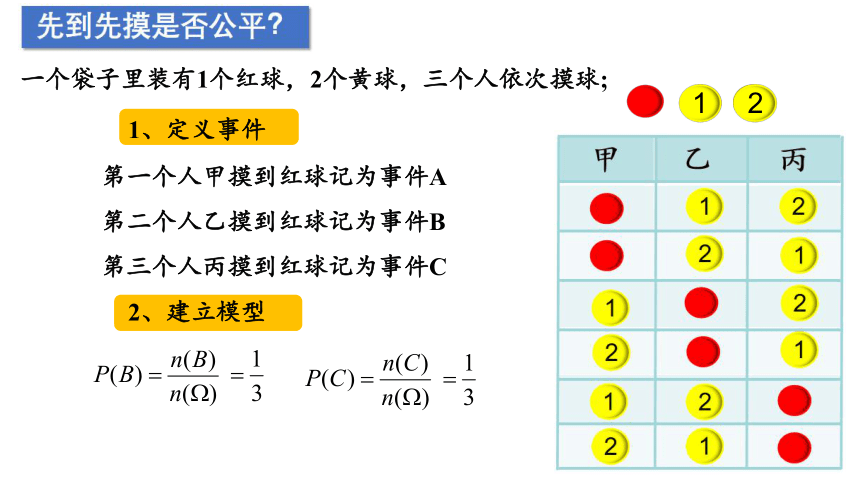
在上班去的路上,小李收到一条来自办公室组长的短信,“各位同仁好!公司分给我们办公室一张2023跨年演唱会入场券,为公平起见,我们组3人采取摸球确定入场券获得者的办法:一个不透明袋子里放入3个大小和质地没有区别的小球,其中1个红球,2个黄球,大家依次从中摸出一个球,摸到红球者获得入场券,先到办公室者可以先摸哦!”
小李看到路上这么堵,心中不悦:“他们肯定比我先到了,这对我不公平!”
请问:小李的担心有道理吗
一个袋子里装有1个红球,2个黄球,三个人依次摸球;
1、定义事件
1
2
2、建立模型
第一个人甲摸到红球记为事件A
第二个人乙摸到红球记为事件B
第三个人丙摸到红球记为事件C
情境二:
等小李赶到办公室时,发现前面只有小王已经摸过球了,但小王摸到的是黄球,小李暗自窃喜:“哈,这下我摸到红球的可能性就大些了!”
请问:小李的想法有道理吗
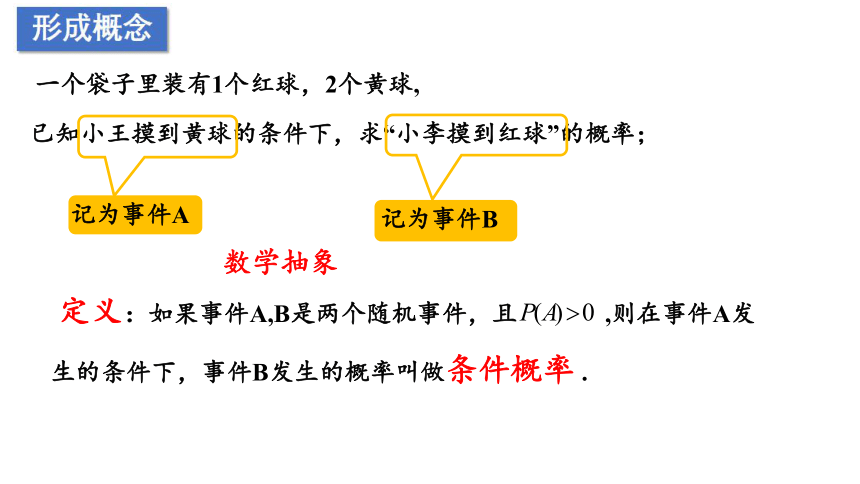
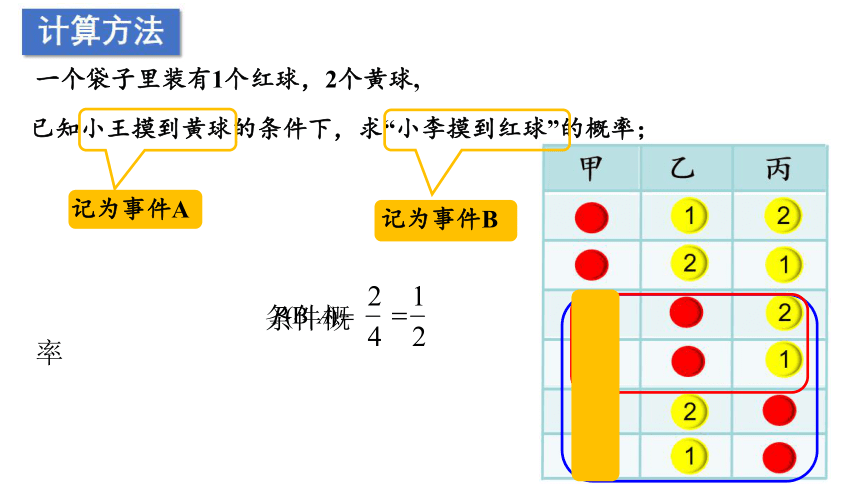
一个袋子里装有1个红球,2个黄球,
已知小王摸到黄球的条件下,求“小李摸到红球”的概率;
记为事件A
记为事件B
定义:如果事件A,B是两个随机事件,且 ,则在事件A发生的条件下,事件B发生的概率叫做条件概率 .
数学抽象
7.1.1条件概率
台州一中 王莎莎
定义:如果事件A,B是两个随机事件,且 ,则在事件A发生的条件下,事件B发生的概率叫做条件概率 .
符号表示:
一个袋子里装有1个红球,2个黄球,
已知小王摸到黄球的条件下,求“小李摸到红球”的概率;
记为事件A
记为事件B
条件概率
缩小了样本空间!
类比迁移
条件概率的本质:在缩小的样本空间上计算事件的概率.
B
A
B
A
例1 某班有45名学生,其中男生、女生的人数及团员的人数如表7.1-1所示.
在班级里随机选择一人做代表.
(1) 选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
记为事件B
记为事件A
例2 已知春季里,每天甲、乙两地下雨的概率分别为
与 ,且两地同时下雨的概率为 ,求春季的
一天里,已知甲地下雨的条件下,乙地也下雨的概率.
记为事件A
记为事件B
在问题1和问题2中,都有 .一般地, 与 不一定相等.如果 与 相等,那么事件A与B应满足什么条件.
相互独立
=
公式变形
由条件概率的定义,对任意两个事件A,B,若 ,则
概率的乘法公式
一个袋子里装有1个红球,2个黄球,三个人依次摸球;
第一个人甲摸到红球记为事件A
第二个人乙摸到红球记为事件B
第三个人丙摸到红球记为事件C
条件概率只是缩小样本空间,因此条件概率同样具有概率的性质 .
(3)如果 和 B 互为对立事件,
则
(1)
概率的性质
条件概率的性质
(1)
(2)如果B和C是两个互斥事件,
则
(2)如果B和C是两个互斥事件,
则
(3)如果 和 B 互为对立事件,
则
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:设 表示第一次按对密码, 表示第二次按对密码
记为事件A
记为事件B
条件概率
计算方法
条件概率
的性质
条件概率的本质:在缩小的样本空间上计算事件的概率.
著名的“三门问题”,也称作“蒙提霍尔悖论”:在美国的一档综艺节目中,嘉宾面前有三扇关闭着的门,其中一扇的后面是一辆汽车,选中后面有车的那扇门就可以赢得该汽车,而另外两扇门后面则各藏有一只山羊。当嘉宾选定了一扇门,但未去开启它的时候,主持人会开启剩下两扇门中的一扇,露出其中一只山羊。主持人其后会问嘉宾要不要更换选择,选另一扇仍然关着的门。请问,此时是否要听从主持人的建议更换选择?
谢
谢
1494年
帕奇欧里提出
赌金分配问题
1654年
帕斯卡与费马通信探讨,概率论奠基人
1657年
惠更斯出版
《论骰子游戏中的推理》
20世纪初
科尔莫戈罗夫建立
严谨的概率论理论体系
01
概率论
1713年
伯努利《猜度术》 大数理论
1812年
拉普拉斯
《分析概率论》
概率论起源与发展
03
05
02
04
06
(研究随机现象数量规律的数学分支)
数学广角
互斥
互为对立
新的概率模型
和事件
积事件
情境一:
在上班去的路上,小李收到一条来自办公室组长的短信,“各位同仁好!公司分给我们办公室一张2023跨年演唱会入场券,为公平起见,我们组3人采取摸球确定入场券获得者的办法:一个不透明袋子里放入3个大小和质地没有区别的小球,其中1个红球,2个黄球,大家依次从中摸出一个球,摸到红球者获得入场券,先到办公室者可以先摸哦!”
小李看到路上这么堵,心中不悦:“他们肯定比我先到了,这对我不公平!”
请问:小李的担心有道理吗
一个袋子里装有1个红球,2个黄球,三个人依次摸球;
1、定义事件
1
2
2、建立模型
第一个人甲摸到红球记为事件A
第二个人乙摸到红球记为事件B
第三个人丙摸到红球记为事件C
情境二:
等小李赶到办公室时,发现前面只有小王已经摸过球了,但小王摸到的是黄球,小李暗自窃喜:“哈,这下我摸到红球的可能性就大些了!”
请问:小李的想法有道理吗
一个袋子里装有1个红球,2个黄球,
已知小王摸到黄球的条件下,求“小李摸到红球”的概率;
记为事件A
记为事件B
定义:如果事件A,B是两个随机事件,且 ,则在事件A发生的条件下,事件B发生的概率叫做条件概率 .
数学抽象
7.1.1条件概率
台州一中 王莎莎
定义:如果事件A,B是两个随机事件,且 ,则在事件A发生的条件下,事件B发生的概率叫做条件概率 .
符号表示:
一个袋子里装有1个红球,2个黄球,
已知小王摸到黄球的条件下,求“小李摸到红球”的概率;
记为事件A
记为事件B
条件概率
缩小了样本空间!
类比迁移
条件概率的本质:在缩小的样本空间上计算事件的概率.
B
A
B
A
例1 某班有45名学生,其中男生、女生的人数及团员的人数如表7.1-1所示.
在班级里随机选择一人做代表.
(1) 选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
记为事件B
记为事件A
例2 已知春季里,每天甲、乙两地下雨的概率分别为
与 ,且两地同时下雨的概率为 ,求春季的
一天里,已知甲地下雨的条件下,乙地也下雨的概率.
记为事件A
记为事件B
在问题1和问题2中,都有 .一般地, 与 不一定相等.如果 与 相等,那么事件A与B应满足什么条件.
相互独立
=
公式变形
由条件概率的定义,对任意两个事件A,B,若 ,则
概率的乘法公式
一个袋子里装有1个红球,2个黄球,三个人依次摸球;
第一个人甲摸到红球记为事件A
第二个人乙摸到红球记为事件B
第三个人丙摸到红球记为事件C
条件概率只是缩小样本空间,因此条件概率同样具有概率的性质 .
(3)如果 和 B 互为对立事件,
则
(1)
概率的性质
条件概率的性质
(1)
(2)如果B和C是两个互斥事件,
则
(2)如果B和C是两个互斥事件,
则
(3)如果 和 B 互为对立事件,
则
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:设 表示第一次按对密码, 表示第二次按对密码
记为事件A
记为事件B
条件概率
计算方法
条件概率
的性质
条件概率的本质:在缩小的样本空间上计算事件的概率.
著名的“三门问题”,也称作“蒙提霍尔悖论”:在美国的一档综艺节目中,嘉宾面前有三扇关闭着的门,其中一扇的后面是一辆汽车,选中后面有车的那扇门就可以赢得该汽车,而另外两扇门后面则各藏有一只山羊。当嘉宾选定了一扇门,但未去开启它的时候,主持人会开启剩下两扇门中的一扇,露出其中一只山羊。主持人其后会问嘉宾要不要更换选择,选另一扇仍然关着的门。请问,此时是否要听从主持人的建议更换选择?
谢
谢
