2023~2024苏科版数学七年级下册第7章 平面图形的认识(二) 单元训练题(含答案)
文档属性
| 名称 | 2023~2024苏科版数学七年级下册第7章 平面图形的认识(二) 单元训练题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 344.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 12:53:02 | ||
图片预览

文档简介
第7章 平面图形的认识(二)章末训练题
一、选择题
1.(2022·四川德阳)八一中学校九年级2班学生杨冲家和李锐家到学校的直线距离分别是和.那么杨冲,李锐两家的直线距离不可能是( )
A. B. C. D.
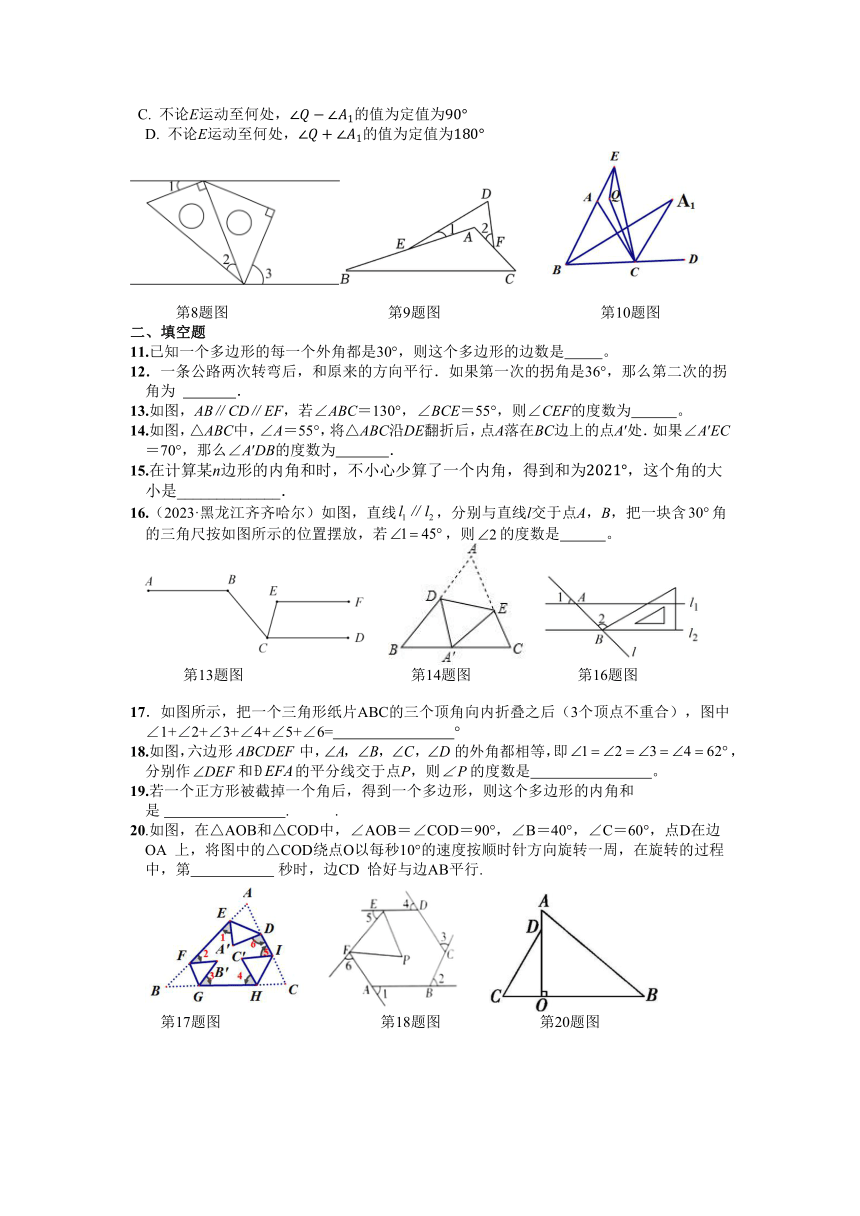
2.(2023·湖北鄂州)如图,直线,于点E.若,则的度数是( )
A. B. C. D.
3.如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面的平移步骤正确的是( )
A.先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度
B.先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度
C.先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度
D.先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度
4.(2023·四川宜宾)如图, ,且,,则等于( )
A. B. C. D.
第2题图 第3题图 第4题图
5.(2022·浙江杭州)如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
A.线段CD是△ABC的AC边上的高线 B.线段CD是△ABC的AB边上的高线
C.线段AD是△ABC的BC边上的高线 D.线段AD是△ABC的AC边上的高线
6.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A.16cm B.18cm C.20cm D.22cm
7.(2023·山西)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点,点为焦点.若,则的度数为( )
A. B. C. D.
第5题图 第6题图 第7题图
8.(2023·黑龙江绥化)将一副三角板按下图所示摆放在一组平行线内,,,则的度数为( )
A. B. C. D.
9.如图,E,F是△ABC的边AB,AC上的点,D是点A上方的一点,若∠B+∠C=64°,∠D=70°,则∠1+∠2的度数为( )
A.44° B.46° C.48° D.50°
10.如图,中,的角平分线与的外角的平分线交于,若E沿着BA延长线运动,连EC,与的角平分线交于Q,当E运动时( )
A. 随着E的运动,的值先减小后增大、
B. 随着E的运动,的值先减小后增大
C. 不论E运动至何处,的值为定值为
D. 不论E运动至何处,的值为定值为
第8题图 第9题图 第10题图
二、填空题
11.已知一个多边形的每一个外角都是30°,则这个多边形的边数是 。
12.一条公路两次转弯后,和原来的方向平行.如果第一次的拐角是36°,那么第二次的拐角为 .
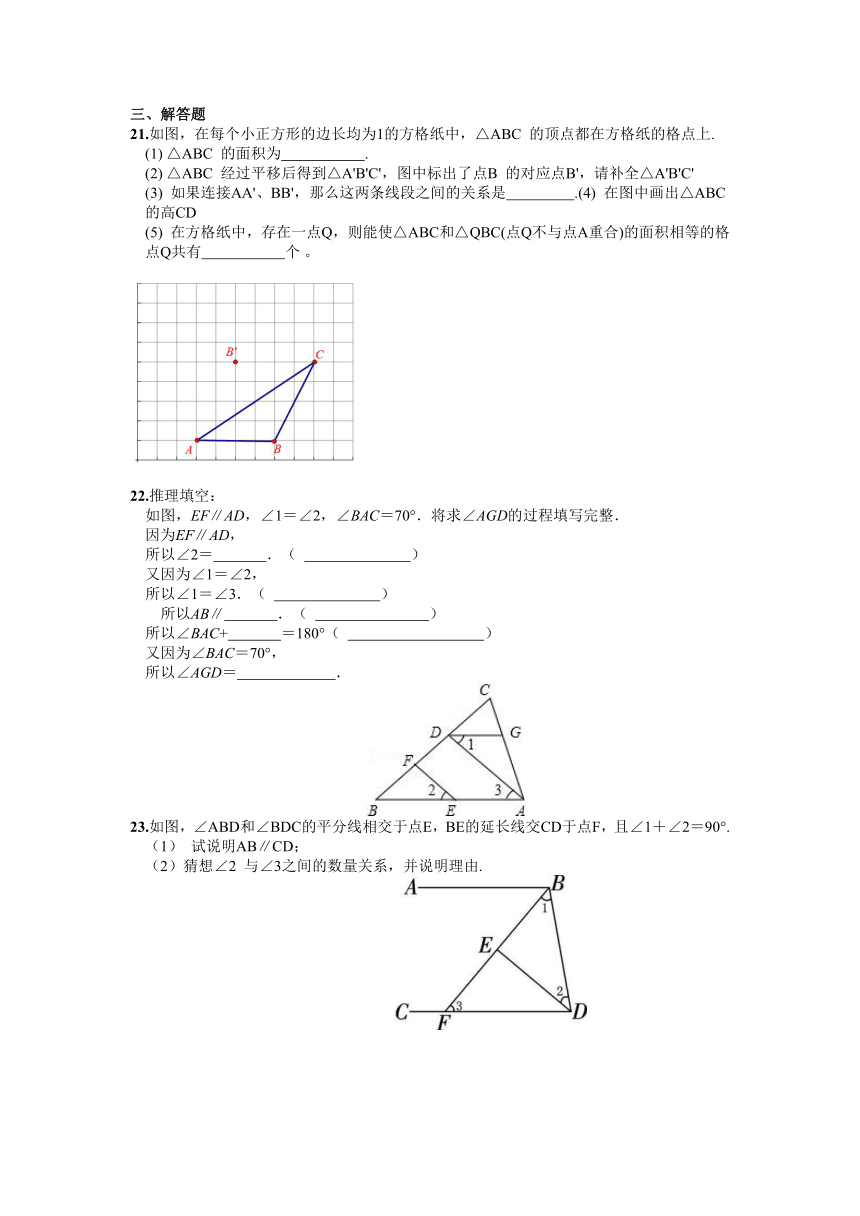
13.如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为 。
14.如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为 .
15.在计算某n边形的内角和时,不小心少算了一个内角,得到和为,这个角的大小是_____________.
16.(2023·黑龙江齐齐哈尔)如图,直线,分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若,则的度数是 。
第13题图 第14题图 第16题图
17.如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),图中∠1+∠2+∠3+∠4+∠5+∠6= °
18.如图,六边形中,的外角都相等,即,分别作和的平分线交于点P,则的度数是 。
19.若一个正方形被截掉一个角后,得到一个多边形,则这个多边形的内角和是 . .
20.如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA 上,将图中的△COD绕点O以每秒10°的速度按顺时针方向旋转一周,在旋转的过程中,第 秒时,边CD 恰好与边AB平行.
第17题图 第18题图 第20题图
三、解答题
21.如图,在每个小正方形的边长均为1的方格纸中,△ABC 的顶点都在方格纸的格点上.
(1) △ABC 的面积为 .
(2) △ABC 经过平移后得到△A'B'C',图中标出了点B 的对应点B',请补全△A'B'C'
(3) 如果连接AA'、BB',那么这两条线段之间的关系是 .(4) 在图中画出△ABC 的高CD
(5) 在方格纸中,存在一点Q,则能使△ABC和△QBC(点Q不与点A重合)的面积相等的格点Q共有 个 。
22.推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .
23.如图,∠ABD和∠BDC的平分线相交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.
(1) 试说明AB∥CD;
(2)猜想∠2 与∠3之间的数量关系,并说明理由.
24.将一副三角板中的两块直角三角尺的直角顶点按如图方式叠放在一起其中,,;:
若,则的度数为______;
若,求的度数;
由猜想与的数量关系,并说明理由.
当且点在直线的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出角度所有可能的值不必说明理由;若不存在,请说明理由
25.在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.
(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由。
参考答案
一、选择题
1.A;2.B;3.A;4.D;5.B;6.C;7.C;8.C;9.B;10.D;
二、填空题
11.12;12.36°或144°;13.105°;14.75°;15.139°;16.105°;17.360°;18.56°;19.180°或360°或540°;20.10或28;
三、解答题
21.8;如图,;平行且相等;4.
22.∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠AGD,两直线平行,同旁内角互补,110°.
23.解:(1) 因为BE、DE分别平分∠ABD、∠BDC,所以∠ABD=2∠1,∠BDC=2∠2.因为∠1 +∠2 = 90°,所以∠ABD+∠BDC=180°.所以AB∥CD
(2) ∠2 +∠3=90° 理由:因为AB∥CD,所以∠ABF=∠3.因为BE平分∠ABD,所以∠ABF=∠1.所以∠1=∠3.因为∠1+∠2=90°,所以∠2+∠3=90°
24.,故答案为:;
,
;
猜想:
理由如下:
又
即;
、、、、.
理由:当时,;
当时,;
当时,;
当时,;
当时,.
25.(1)由翻折的性质可得:∠E=∠B,
∵∠BAC=90°,AE⊥BC,
∴∠DFE=90°,
∴180°-∠BAC=180°-∠DFE=90°,
即:∠B+∠C=∠E+∠FDE=90°,
∴∠C=∠FDE,
∴AC∥DE,
∴∠CAF=∠E,
∴∠CAF=∠E=∠B
故与∠B相等的角有∠CAF和∠E;
∵∠BAC=90°,AE⊥BC,
∴∠BAF+∠CAF=90°, ∠CFA=180°-(∠CAF+∠C)=90°
∴∠BAF+∠CAF=∠CAF+∠C=90°
∴∠BAF=∠C
又AC∥DE,
∴∠C=∠CDE,
∴故与∠C相等的角有∠CDE、∠BAF;
(2)①∵
∴
又∵,
∴∠C=70°,∠B=20°;
②∵∠BAD=x°, ∠B=20°则,,
由翻折可知:∵, ,
∴, ,
当∠FDE=∠DFE时,, 解得:;
当∠FDE=∠E时,,解得:(因为0<x≤45,故舍去);
当∠DFE=∠E时,,解得:(因为0<x≤45,故舍去);
综上所述,存在这样的x的值,使得△DEF中有两个角相等.且.
一、选择题
1.(2022·四川德阳)八一中学校九年级2班学生杨冲家和李锐家到学校的直线距离分别是和.那么杨冲,李锐两家的直线距离不可能是( )
A. B. C. D.
2.(2023·湖北鄂州)如图,直线,于点E.若,则的度数是( )
A. B. C. D.
3.如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面的平移步骤正确的是( )
A.先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度
B.先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度
C.先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度
D.先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度
4.(2023·四川宜宾)如图, ,且,,则等于( )
A. B. C. D.
第2题图 第3题图 第4题图
5.(2022·浙江杭州)如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
A.线段CD是△ABC的AC边上的高线 B.线段CD是△ABC的AB边上的高线
C.线段AD是△ABC的BC边上的高线 D.线段AD是△ABC的AC边上的高线
6.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A.16cm B.18cm C.20cm D.22cm
7.(2023·山西)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点,点为焦点.若,则的度数为( )
A. B. C. D.
第5题图 第6题图 第7题图
8.(2023·黑龙江绥化)将一副三角板按下图所示摆放在一组平行线内,,,则的度数为( )
A. B. C. D.
9.如图,E,F是△ABC的边AB,AC上的点,D是点A上方的一点,若∠B+∠C=64°,∠D=70°,则∠1+∠2的度数为( )
A.44° B.46° C.48° D.50°
10.如图,中,的角平分线与的外角的平分线交于,若E沿着BA延长线运动,连EC,与的角平分线交于Q,当E运动时( )
A. 随着E的运动,的值先减小后增大、
B. 随着E的运动,的值先减小后增大
C. 不论E运动至何处,的值为定值为
D. 不论E运动至何处,的值为定值为
第8题图 第9题图 第10题图
二、填空题
11.已知一个多边形的每一个外角都是30°,则这个多边形的边数是 。
12.一条公路两次转弯后,和原来的方向平行.如果第一次的拐角是36°,那么第二次的拐角为 .
13.如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为 。
14.如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为 .
15.在计算某n边形的内角和时,不小心少算了一个内角,得到和为,这个角的大小是_____________.
16.(2023·黑龙江齐齐哈尔)如图,直线,分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若,则的度数是 。
第13题图 第14题图 第16题图
17.如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),图中∠1+∠2+∠3+∠4+∠5+∠6= °
18.如图,六边形中,的外角都相等,即,分别作和的平分线交于点P,则的度数是 。
19.若一个正方形被截掉一个角后,得到一个多边形,则这个多边形的内角和是 . .
20.如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA 上,将图中的△COD绕点O以每秒10°的速度按顺时针方向旋转一周,在旋转的过程中,第 秒时,边CD 恰好与边AB平行.
第17题图 第18题图 第20题图
三、解答题
21.如图,在每个小正方形的边长均为1的方格纸中,△ABC 的顶点都在方格纸的格点上.
(1) △ABC 的面积为 .
(2) △ABC 经过平移后得到△A'B'C',图中标出了点B 的对应点B',请补全△A'B'C'
(3) 如果连接AA'、BB',那么这两条线段之间的关系是 .(4) 在图中画出△ABC 的高CD
(5) 在方格纸中,存在一点Q,则能使△ABC和△QBC(点Q不与点A重合)的面积相等的格点Q共有 个 。
22.推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .
23.如图,∠ABD和∠BDC的平分线相交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.
(1) 试说明AB∥CD;
(2)猜想∠2 与∠3之间的数量关系,并说明理由.
24.将一副三角板中的两块直角三角尺的直角顶点按如图方式叠放在一起其中,,;:
若,则的度数为______;
若,求的度数;
由猜想与的数量关系,并说明理由.
当且点在直线的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出角度所有可能的值不必说明理由;若不存在,请说明理由
25.在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.
(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由。
参考答案
一、选择题
1.A;2.B;3.A;4.D;5.B;6.C;7.C;8.C;9.B;10.D;
二、填空题
11.12;12.36°或144°;13.105°;14.75°;15.139°;16.105°;17.360°;18.56°;19.180°或360°或540°;20.10或28;
三、解答题
21.8;如图,;平行且相等;4.
22.∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠AGD,两直线平行,同旁内角互补,110°.
23.解:(1) 因为BE、DE分别平分∠ABD、∠BDC,所以∠ABD=2∠1,∠BDC=2∠2.因为∠1 +∠2 = 90°,所以∠ABD+∠BDC=180°.所以AB∥CD
(2) ∠2 +∠3=90° 理由:因为AB∥CD,所以∠ABF=∠3.因为BE平分∠ABD,所以∠ABF=∠1.所以∠1=∠3.因为∠1+∠2=90°,所以∠2+∠3=90°
24.,故答案为:;
,
;
猜想:
理由如下:
又
即;
、、、、.
理由:当时,;
当时,;
当时,;
当时,;
当时,.
25.(1)由翻折的性质可得:∠E=∠B,
∵∠BAC=90°,AE⊥BC,
∴∠DFE=90°,
∴180°-∠BAC=180°-∠DFE=90°,
即:∠B+∠C=∠E+∠FDE=90°,
∴∠C=∠FDE,
∴AC∥DE,
∴∠CAF=∠E,
∴∠CAF=∠E=∠B
故与∠B相等的角有∠CAF和∠E;
∵∠BAC=90°,AE⊥BC,
∴∠BAF+∠CAF=90°, ∠CFA=180°-(∠CAF+∠C)=90°
∴∠BAF+∠CAF=∠CAF+∠C=90°
∴∠BAF=∠C
又AC∥DE,
∴∠C=∠CDE,
∴故与∠C相等的角有∠CDE、∠BAF;
(2)①∵
∴
又∵,
∴∠C=70°,∠B=20°;
②∵∠BAD=x°, ∠B=20°则,,
由翻折可知:∵, ,
∴, ,
当∠FDE=∠DFE时,, 解得:;
当∠FDE=∠E时,,解得:(因为0<x≤45,故舍去);
当∠DFE=∠E时,,解得:(因为0<x≤45,故舍去);
综上所述,存在这样的x的值,使得△DEF中有两个角相等.且.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
