第八章 成对数据的统计分析 章末检测试卷三(含解析) -2024春高中数学选择性必修3(人教版)
文档属性
| 名称 | 第八章 成对数据的统计分析 章末检测试卷三(含解析) -2024春高中数学选择性必修3(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 13:12:43 | ||
图片预览




文档简介
第八章 成对数据的统计分析 章末检测试卷三
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在一项中学生近视情况的调查中,某校150名男生中有80名近视,140名女生中有70名近视,在检验这些中学生眼睛近视是否与性别有关时最有说服力的方法是( )
A.平均数与方差 B.回归分析
C.独立性检验 D.概率
2.甲、乙、丙、丁四位同学各自对A,B两变量做回归分析,分别得到散点图与残差平方和(yi-i)2如表:
甲 乙 丙 丁
散点图
残差平方和 115 106 124 103
实验结果体现出拟合A,B两变量之间关系的模型精度最高的是( )
A.甲 B.乙 C.丙 D.丁
3.船员人数y关于船的吨位x的经验回归方程是=95+0.06x.若两艘轮船吨位相差1 000吨,则船员平均人数相差( )
A.40 B.57
C.60 D.95
4.在2×2列联表中,若每个数据变为原来的2倍,则χ2的值变为原来的( )
A.8倍 B.4倍
C.2倍 D.不变
5.为了评价某个电视栏目的改革效果,某机构在改革前后分别从居民点抽取了100位居民进行调查,经过计算χ2≈0.99,根据这一数据分析,下列说法正确的是( )
A.有99%的人认为该电视栏目优秀
B.有99%的人认为该电视栏目是否优秀与改革有关系
C.在犯错误的概率不超过1%的前提下,认为该电视栏目是否优秀与改革有关系
D.没有理由认为该电视栏目是否优秀与改革有关系
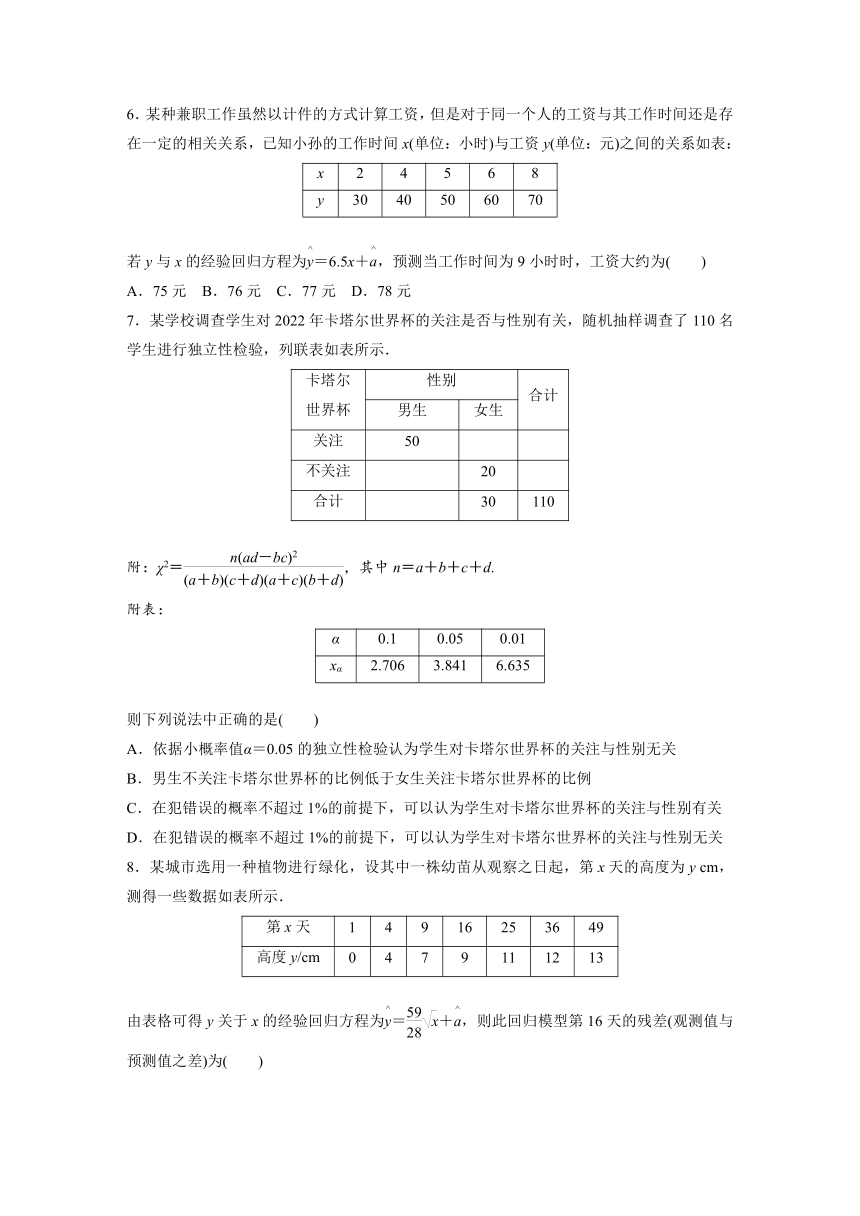
6.某种兼职工作虽然以计件的方式计算工资,但是对于同一个人的工资与其工作时间还是存在一定的相关关系,已知小孙的工作时间x(单位:小时)与工资y(单位:元)之间的关系如表:
x 2 4 5 6 8
y 30 40 50 60 70
若y与x的经验回归方程为=6.5x+,预测当工作时间为9小时时,工资大约为( )
A.75元 B.76元 C.77元 D.78元
7.某学校调查学生对2022年卡塔尔世界杯的关注是否与性别有关,随机抽样调查了110名学生进行独立性检验,列联表如表所示.
卡塔尔世界杯 性别 合计
男生 女生
关注 50
不关注 20
合计 30 110
附:χ2=,其中n=a+b+c+d.
附表:
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
则下列说法中正确的是( )
A.依据小概率值α=0.05的独立性检验认为学生对卡塔尔世界杯的关注与性别无关
B.男生不关注卡塔尔世界杯的比例低于女生关注卡塔尔世界杯的比例
C.在犯错误的概率不超过1%的前提下,可以认为学生对卡塔尔世界杯的关注与性别有关
D.在犯错误的概率不超过1%的前提下,可以认为学生对卡塔尔世界杯的关注与性别无关
8.某城市选用一种植物进行绿化,设其中一株幼苗从观察之日起,第x天的高度为y cm,测得一些数据如表所示.
第x天 1 4 9 16 25 36 49
高度y/cm 0 4 7 9 11 12 13
由表格可得y关于x的经验回归方程为=+,则此回归模型第16天的残差(观测值与预测值之差)为( )
A.- B. C.0 D.1
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩,得到如下2×2列联表:
班级 成绩 合计
优秀 非优秀
甲班 10 b
乙班 c 30
合计 105
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为20,b的值为45
C.根据列联表中的数据,在犯错误的概率不超过0.05的前提下认为“成绩与班级有关系”
D.根据列联表中的数据,在犯错误的概率不超过0.01的前提下认为“成绩与班级有关系”
10.已知变量x,y之间的经验回归方程为=-0.7x+10.3,且变量x,y之间的一组相关数据如表所示,则下列说法正确的是( )
x 6 8 10 12
y 6 m 3 2
A.变量x,y之间呈负相关
B.m=4
C.可以预测,当x=11时,y约为2.6
D.由表格数据知,该经验回归直线必过点(9,4)
11.某大学为了解学生对学校食堂服务的满意度,随机调查了50名男生和50名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如表所示的列联表.经计算χ2≈4.762,则可以推断出( )
性别 评价 合计
满意 不满意
男 30 20 50
女 40 10 50
合计 70 30 100
A.该学校男生对食堂服务满意的概率的估计值为
B.调研结果显示,该学校男生比女生对食堂服务更满意
C.依据小概率值α=0.05的独立性检验,可以认为男、女生对该食堂服务的评价有差异
D.依据小概率值α=0.01的独立性检验,可以认为男、女生对该食堂服务的评价有差异
12.已知由样本数据点集合 {(xi,yi)|i=1,2,…,n},求得的经验回归方程为=1.5x+0.5,且=3,现发现两个数据点(1.2,2.2)和(4.8,7.8)误差较大,去除后重新求得的经验回归直线l的斜率为1.2,则( )
A.变量x与y具有正相关关系
B.去除后y的估计值增长速度变快
C.去除后l的方程为=1.2x+1.4
D.去除后的样本点(2,3.75)的残差为-0.05
三、填空题(本题共4小题,每小题5分,共20分)
13.根据如表所示数据所求得的经验回归方程为=4x+242,则实数a=________.
x 2 3 4 5 6
y 251 254 257 a 266
14.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足yi=xi++ei(i=1,2,…,n),且ei=0,则R2为________.
15.某高校《统计初步》课程的教师随机调查了选该课的学生的一些情况,具体数据如表:
性别 主修专业 合计
非统计专业 统计专业
男 13 10 23
女 7 20 27
合计 20 20 50
则χ2≈________,认为主修统计专业与性别有关的犯错误的概率不超过________.
16.下面是一个2×2列联表:
X Y 合计
Y1 Y2
X1 a 21 70
X2 5 c 30
合计 b d 100
则b-d=________,χ2≈________.(保留小数点后3位)
四、解答题(本题共6小题,共70分)
17.(10分)有关部门对某校小学生进行心理障碍测试,得到如下2×2列联表:
性别 心理障碍 合计
有 没有
女生 10 30
男生 70 80
合计 20 110
将表格填写完整,试说明心理障碍与性别是否有关.
附:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
18.(12分)某地区2016年至2022年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 2016 2017 2018 2019 2020 2021 2022
年份代号t 1 2 3 4 5 6 7
人均纯收入y 2.9 3.3 3.6 4.4 4.8 5.2 5.9
(1)求y关于t的经验回归方程;
(2)利用(1)中的经验回归方程,分析2016年至2022年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2024年农村居民家庭人均纯收入.
附:经验回归直线的斜率和截距的最小二乘估计公式分别为
=,=-.
19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
(xi-)2 (wi-)2 (xi-) (yi-) (wi-)· (yi-)
46.6 563 6.8 289.8 1.6 1 469 108.8
表中wi=,=i.
(1)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的经验回归模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的经验回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果计算当年宣传费x为何值时,年利润的预测值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归直线=+u的斜率和截距的最小二乘估计分别为=,=-.
20.(12分)当前,“日行万步”正式成为健康生活的代名词.某地一研究团队统计了该地区1 000位居民的日行步数,得到如下表格.
日行步数 (单位:千步) [0,2] (2,4] (4,6] (6,8] (8,10] (10,12] (12,14]
人数 20 60 170 200 300 200 50
为研究日行步数与居民年龄的关系,以日行步数是否超过8千步进行比例分配的分层随机抽样,从上述1 000位居民中抽取200人.
(1)请将下面的列联表补充完整;
年龄 日行步数 合计
不超过8千步 超过8千步
40岁以上 100
40岁以下(含40岁) 50
合计 200
(2)依据小概率值α=0.05的独立性检验,能否认为日行步数与居民年龄有关?
附:χ2=,其中n=a+b+c+d.
α 0.05 0.025 0.010
xα 3.841 5.024 6.635
21.(12分)溺水、校园欺凌、食品卫生、消防安全、道路交通等与学生安全有关的问题越来越受到社会的关注和重视.学校安全工作事关学生的健康成长,关系到千万个家庭的幸福和安宁,关系到整个社会的和谐稳定.为了普及安全教育,某市准备组织一次安全知识竞赛.某学校为了选拔学生参赛,按性别采用比例分配的分层随机抽样的方法抽取200名学生进行安全知识测试,根据200名同学的测试成绩得到如下列联表:
性别 安全知识测试 合计
得分不超过85分的人数 得分超过85分的人数
男生 20 100 120
女生 30 50 80
合计 50 150 200
(1)现从得分超过85分的学生中根据性别采用比例分配的分层随机抽样方法抽取6名学生进行安全知识培训,再从这6名学生中随机抽取3名学生去市里参加竞赛,求这3名学生中至少有一名女生的概率;
(2)根据小概率值α=0.001的独立性检验,能否推断该校学生了解安全知识的程度与性别有关?
附:参考公式χ2=,其中n=a+b+c+d.
附表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
22.(12分)某地质探测队为探测一矿中金属锂的分布情况,先设了1个原点,再确定了5个采样点,这5个采样点到原点距离分别为xi,其中xi=i(i=1,2,3,4,5),并得到了各采样点金属锂的含量yi,得到一组数据(xi,yi),i=1,2,3,4,5,经计算得到如下统计量的值:
i=62,(xi-)(yi-)=47,i≈4.79,
(ui-)2≈1.615,(ui-)(yi-)≈19.38,其中ui=ln xi,i=1,2,3,4,5.
(1)利用样本相关系数判断y=a+bx与y=a+bln x哪一个更适宜作为y关于x的经验回归模型;
(2)建立y关于x的经验回归方程.
参考公式:经验回归方程=+t中斜率、截距的最小二乘估计公式、样本相关系数公式分别为==,=- ,
r=;
参考数据:=232.56.
章末检测试卷三(第八章)
1.C
2.D [根据散点图中各样本点条状分布越均匀,同时保持残差平方和越小,其线性回归模型的拟合效果就越好,由此知丁同学的线性回归模型的拟合效果最好.]
3.C [由题意知,经验回归方程是=95+0.06x,两艘轮船吨位相差1 000吨,所以船员平均人数的差值是0.06×1 000=60.]
4.C [由公式
χ2=中所有值变为原来的2倍,
得(χ2)′==2χ2,故χ2也变为原来的2倍.]
5.D [只有χ2≥6.635=x0.01时才能在犯错误的概率不超过1%的前提下,认为该电视栏目是否优秀与改革有关系,而即使χ2≥6.635也只是对“该电视栏目是否优秀与改革有关系”这个论断成立的可能性大小的推论,与是否有99%的人等无关.]
6.B [由表格数据知
==5,
==50,
∴=-6.5=50-32.5=17.5,
∴经验回归方程为=6.5x+17.5,
∴6.5×9+17.5=76(元),即当工作时间为9小时时,工资大约为76元.]
7.C [列联表如下.
卡塔尔世界杯 性别 合计
男生 女生
关注 50 10 60
不关注 30 20 50
合计 80 30 110
则χ2=≈7.486.
对于A,χ2≈7.486>3.841=x0.05,依据小概率值α=0.05的独立性检验,认为学生对卡塔尔世界杯的关注与性别有关,故A错误;
对于B,男生不关注卡塔尔世界杯的比例为=,女生关注卡塔尔世界杯的比例为=,且>,则男生不关注卡塔尔世界杯的比例高于女生关注卡塔尔世界杯的比例,故B错误;
对于C,D,χ2≈7.486>6.635=x0.01,则在犯错误的概率不超过1%的前提下,可以认为学生对卡塔尔世界杯的关注与性别有关,故C正确,D错误.]
8.D [设=t,
则==4,
==8,
代入得=8-×4=-,
则=-,
当x=16时,=×4-=8,
则第16天的残差为9-8=1.]
9.BC [由题意知成绩优秀的学生数是30,成绩非优秀的学生数是75,
所以c=20,b=45,故A错误,B正确;
根据列联表中的数据,得到χ2=
≈6.109>3.841=x0.05,而χ2≈6.109<6.635=x0.01,
因此在犯错误的概率不超过0.05的前提下认为“成绩与班级有关系”,故C正确,D错误.]
10.ACD [由=-0.7x+10.3得=-0.7<0,所以x,y呈负相关,故A正确;
当x=11时,y的预测值为2.6,故C正确;
由==9,
得=-0.7×9+10.3=4.
故经验回归直线过(9,4),故D正确;
因为=4,所以=4,解得m=5,故B错误.]
11.AC [对于选项A,该学校男生对食堂服务满意的概率的估计值为=,故A正确;
对于选项B,该学校女生对食堂服务满意的概率的估计值为=>,故B错误;
因为χ2≈4.762>3.841=x0.05,且χ2≈4.762<6.635=x0.01,所以依据小概率值α=0.05的独立性检验,可以认为男、女生对该食堂服务的评价有差异,故C正确,D错误.]
12.ACD [将=3,代入=1.5x+0.5,得=5,因为重新求得的回归直线l的斜率为1.2,故变量x与y具有正相关关系,故A正确;
设新的数据所有的横坐标的平均值为1,则(n-2)1=n-(1.2+4.8)=3n-6=3(n-2),故 1=3,
设纵坐标的平均值为1,则(n-2)1=n-(2.2+7.8)=5n-10=5(n-2), 1=5,设新的经验回归方程为=1.2x+,把(3,5)代入得5=1.2×3+,=1.4,故新的经验回归方程为=1.2x+1.4,故C正确;
因为1.5>1.2,所以y的增长速度变慢,故B错误;
把x=2代入新的经验回归方程,得=3.8,3.75-3.8=-0.05,故D正确.]
13.262
解析 由题意,得=4,
=(1 028+a),
代入=4x+242,
可得(1 028+a)=4×4+242,解得a=262.
14.1
解析 由ei=0,知yi=i,
即yi-i=0,
故R2=1-=1-0=1.
15.4.844 0.05
解析 χ2=≈4.844>3.841=x0.05,根据小概率值α=0.05的独立性检验,可知认为主修统计专业与性别有关,此推断犯错误的概率不超过0.05.
16.8 24.047
解析 由2×2列联表得
a=49,b=54,c=25,d=46.
∴b-d=54-46=8.
χ2=
≈24.047.
17.解 补充列联表如表:
性别 心理障碍 合计
有 没有
女生 10 20 30
男生 10 70 80
合计 20 90 110
零假设为H0:心理障碍与性别无关.
根据列联表中的数据,经计算得
χ2=
≈6.366>3.841=x0.05.
根据小概率值α=0.05的独立性检验,可以认为H0不成立.即认为心理障碍与性别有关,此判断犯错误的概率不超过0.05.
18.解 (1)由所给数据计算得
=×(1+2+3+4+5+6+7)=4,
=×(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
(ti-)2=9+4+1+0+1+4+9=28,
(ti-)(yi-)
=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
===0.5,
=-=4.3-0.5×4=2.3,
故所求经验回归方程为=0.5t+2.3.
(2)由(1)知,=0.5>0,故2016年至2022年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2024年的年份代号t=9代入(1)中的经验回归方程,
得=0.5×9+2.3=6.8(千元),
故预测该地区2024年农村居民家庭人均纯收入为6.8千元.
19.解 (1)由散点图知各点呈非线性递增趋势,
所以y=c+d作为经验回归模型比较合适.
(2)由wi=,
则===68,
由=6.8,=563,
得=- =563-68×6.8=100.6,
所以=100.6+68.
(3)根据(2)的结果知,年利润z的预测值=0.2(100.6+68)-x=20.12+13.6-()2=-(-6.8)2+66.36,
所以当=6.8,即x=46.24时,年利润的预测值最大.
20.解 (1)1 000人中,步数不超过8千步的有20+60+170+200=450(人),步数超过8千步的有550人,用比例分配的分层随机抽样方法,抽取的人数中不超过8千步的有90人,超过8千步的有110人,
故40岁以上且日行步数不超过8千步的有40人,40岁以上且日行步数超过8千步的有60人,
40岁以下(含40岁)日行步数超过8千步的有50人,合计40岁以下(含40岁)的人数为100人,
补全的列联表如下.
年龄 日行步数 合计
不超过8千步 超过8千步
40岁以上 40 60 100
40岁以下(含40岁) 50 50 100
合计 90 110 200
(2)零假设为H0:日行步数与居民年龄无关,
计算得χ2
=≈2.02<3.841=x0.05,
根据小概率值α=0.05的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,
即认为日行步数与居民年龄无关.
21.解 (1)200名学生中得分超过85分的人数为150,其中男生人数为100,女生人数为50,
因此样本中男生人数为×6=4,
样本中女生人数为×6=2,
设“这3名学生中至少有一名女生”为事件A,则
P(A)=1-=1-=.
(2)零假设为H0:了解安全知识的程度与性别无关,计算可得χ2==
≈11.11>10.828=x0.001,
根据小概率值α=0.001的独立性检验,
我们认为了解安全知识的程度与性别有关,
此推断犯错误的概率不大于0.001.
22.解 (1)若用y=a+bx作为经验回归模型,
则==3,(xi-)2=(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2=10,
所以样本相关系数r1==,
若用y=a+bln x作为经验回归模型,
样本相关系数r2=
=,
比较r与r,
r==,
r==,
因为r(2)由(1)得===12,
=i=×4.79=0.958,
=i=×62=12.4,
=-=12.4-12×0.958=0.904,
则y关于x的经验回归方程为=0.904+12ln x.
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在一项中学生近视情况的调查中,某校150名男生中有80名近视,140名女生中有70名近视,在检验这些中学生眼睛近视是否与性别有关时最有说服力的方法是( )
A.平均数与方差 B.回归分析
C.独立性检验 D.概率
2.甲、乙、丙、丁四位同学各自对A,B两变量做回归分析,分别得到散点图与残差平方和(yi-i)2如表:
甲 乙 丙 丁
散点图
残差平方和 115 106 124 103
实验结果体现出拟合A,B两变量之间关系的模型精度最高的是( )
A.甲 B.乙 C.丙 D.丁
3.船员人数y关于船的吨位x的经验回归方程是=95+0.06x.若两艘轮船吨位相差1 000吨,则船员平均人数相差( )
A.40 B.57
C.60 D.95
4.在2×2列联表中,若每个数据变为原来的2倍,则χ2的值变为原来的( )
A.8倍 B.4倍
C.2倍 D.不变
5.为了评价某个电视栏目的改革效果,某机构在改革前后分别从居民点抽取了100位居民进行调查,经过计算χ2≈0.99,根据这一数据分析,下列说法正确的是( )
A.有99%的人认为该电视栏目优秀
B.有99%的人认为该电视栏目是否优秀与改革有关系
C.在犯错误的概率不超过1%的前提下,认为该电视栏目是否优秀与改革有关系
D.没有理由认为该电视栏目是否优秀与改革有关系
6.某种兼职工作虽然以计件的方式计算工资,但是对于同一个人的工资与其工作时间还是存在一定的相关关系,已知小孙的工作时间x(单位:小时)与工资y(单位:元)之间的关系如表:
x 2 4 5 6 8
y 30 40 50 60 70
若y与x的经验回归方程为=6.5x+,预测当工作时间为9小时时,工资大约为( )
A.75元 B.76元 C.77元 D.78元
7.某学校调查学生对2022年卡塔尔世界杯的关注是否与性别有关,随机抽样调查了110名学生进行独立性检验,列联表如表所示.
卡塔尔世界杯 性别 合计
男生 女生
关注 50
不关注 20
合计 30 110
附:χ2=,其中n=a+b+c+d.
附表:
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
则下列说法中正确的是( )
A.依据小概率值α=0.05的独立性检验认为学生对卡塔尔世界杯的关注与性别无关
B.男生不关注卡塔尔世界杯的比例低于女生关注卡塔尔世界杯的比例
C.在犯错误的概率不超过1%的前提下,可以认为学生对卡塔尔世界杯的关注与性别有关
D.在犯错误的概率不超过1%的前提下,可以认为学生对卡塔尔世界杯的关注与性别无关
8.某城市选用一种植物进行绿化,设其中一株幼苗从观察之日起,第x天的高度为y cm,测得一些数据如表所示.
第x天 1 4 9 16 25 36 49
高度y/cm 0 4 7 9 11 12 13
由表格可得y关于x的经验回归方程为=+,则此回归模型第16天的残差(观测值与预测值之差)为( )
A.- B. C.0 D.1
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩,得到如下2×2列联表:
班级 成绩 合计
优秀 非优秀
甲班 10 b
乙班 c 30
合计 105
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为20,b的值为45
C.根据列联表中的数据,在犯错误的概率不超过0.05的前提下认为“成绩与班级有关系”
D.根据列联表中的数据,在犯错误的概率不超过0.01的前提下认为“成绩与班级有关系”
10.已知变量x,y之间的经验回归方程为=-0.7x+10.3,且变量x,y之间的一组相关数据如表所示,则下列说法正确的是( )
x 6 8 10 12
y 6 m 3 2
A.变量x,y之间呈负相关
B.m=4
C.可以预测,当x=11时,y约为2.6
D.由表格数据知,该经验回归直线必过点(9,4)
11.某大学为了解学生对学校食堂服务的满意度,随机调查了50名男生和50名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如表所示的列联表.经计算χ2≈4.762,则可以推断出( )
性别 评价 合计
满意 不满意
男 30 20 50
女 40 10 50
合计 70 30 100
A.该学校男生对食堂服务满意的概率的估计值为
B.调研结果显示,该学校男生比女生对食堂服务更满意
C.依据小概率值α=0.05的独立性检验,可以认为男、女生对该食堂服务的评价有差异
D.依据小概率值α=0.01的独立性检验,可以认为男、女生对该食堂服务的评价有差异
12.已知由样本数据点集合 {(xi,yi)|i=1,2,…,n},求得的经验回归方程为=1.5x+0.5,且=3,现发现两个数据点(1.2,2.2)和(4.8,7.8)误差较大,去除后重新求得的经验回归直线l的斜率为1.2,则( )
A.变量x与y具有正相关关系
B.去除后y的估计值增长速度变快
C.去除后l的方程为=1.2x+1.4
D.去除后的样本点(2,3.75)的残差为-0.05
三、填空题(本题共4小题,每小题5分,共20分)
13.根据如表所示数据所求得的经验回归方程为=4x+242,则实数a=________.
x 2 3 4 5 6
y 251 254 257 a 266
14.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足yi=xi++ei(i=1,2,…,n),且ei=0,则R2为________.
15.某高校《统计初步》课程的教师随机调查了选该课的学生的一些情况,具体数据如表:
性别 主修专业 合计
非统计专业 统计专业
男 13 10 23
女 7 20 27
合计 20 20 50
则χ2≈________,认为主修统计专业与性别有关的犯错误的概率不超过________.
16.下面是一个2×2列联表:
X Y 合计
Y1 Y2
X1 a 21 70
X2 5 c 30
合计 b d 100
则b-d=________,χ2≈________.(保留小数点后3位)
四、解答题(本题共6小题,共70分)
17.(10分)有关部门对某校小学生进行心理障碍测试,得到如下2×2列联表:
性别 心理障碍 合计
有 没有
女生 10 30
男生 70 80
合计 20 110
将表格填写完整,试说明心理障碍与性别是否有关.
附:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
18.(12分)某地区2016年至2022年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 2016 2017 2018 2019 2020 2021 2022
年份代号t 1 2 3 4 5 6 7
人均纯收入y 2.9 3.3 3.6 4.4 4.8 5.2 5.9
(1)求y关于t的经验回归方程;
(2)利用(1)中的经验回归方程,分析2016年至2022年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2024年农村居民家庭人均纯收入.
附:经验回归直线的斜率和截距的最小二乘估计公式分别为
=,=-.
19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
(xi-)2 (wi-)2 (xi-) (yi-) (wi-)· (yi-)
46.6 563 6.8 289.8 1.6 1 469 108.8
表中wi=,=i.
(1)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的经验回归模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的经验回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果计算当年宣传费x为何值时,年利润的预测值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归直线=+u的斜率和截距的最小二乘估计分别为=,=-.
20.(12分)当前,“日行万步”正式成为健康生活的代名词.某地一研究团队统计了该地区1 000位居民的日行步数,得到如下表格.
日行步数 (单位:千步) [0,2] (2,4] (4,6] (6,8] (8,10] (10,12] (12,14]
人数 20 60 170 200 300 200 50
为研究日行步数与居民年龄的关系,以日行步数是否超过8千步进行比例分配的分层随机抽样,从上述1 000位居民中抽取200人.
(1)请将下面的列联表补充完整;
年龄 日行步数 合计
不超过8千步 超过8千步
40岁以上 100
40岁以下(含40岁) 50
合计 200
(2)依据小概率值α=0.05的独立性检验,能否认为日行步数与居民年龄有关?
附:χ2=,其中n=a+b+c+d.
α 0.05 0.025 0.010
xα 3.841 5.024 6.635
21.(12分)溺水、校园欺凌、食品卫生、消防安全、道路交通等与学生安全有关的问题越来越受到社会的关注和重视.学校安全工作事关学生的健康成长,关系到千万个家庭的幸福和安宁,关系到整个社会的和谐稳定.为了普及安全教育,某市准备组织一次安全知识竞赛.某学校为了选拔学生参赛,按性别采用比例分配的分层随机抽样的方法抽取200名学生进行安全知识测试,根据200名同学的测试成绩得到如下列联表:
性别 安全知识测试 合计
得分不超过85分的人数 得分超过85分的人数
男生 20 100 120
女生 30 50 80
合计 50 150 200
(1)现从得分超过85分的学生中根据性别采用比例分配的分层随机抽样方法抽取6名学生进行安全知识培训,再从这6名学生中随机抽取3名学生去市里参加竞赛,求这3名学生中至少有一名女生的概率;
(2)根据小概率值α=0.001的独立性检验,能否推断该校学生了解安全知识的程度与性别有关?
附:参考公式χ2=,其中n=a+b+c+d.
附表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
22.(12分)某地质探测队为探测一矿中金属锂的分布情况,先设了1个原点,再确定了5个采样点,这5个采样点到原点距离分别为xi,其中xi=i(i=1,2,3,4,5),并得到了各采样点金属锂的含量yi,得到一组数据(xi,yi),i=1,2,3,4,5,经计算得到如下统计量的值:
i=62,(xi-)(yi-)=47,i≈4.79,
(ui-)2≈1.615,(ui-)(yi-)≈19.38,其中ui=ln xi,i=1,2,3,4,5.
(1)利用样本相关系数判断y=a+bx与y=a+bln x哪一个更适宜作为y关于x的经验回归模型;
(2)建立y关于x的经验回归方程.
参考公式:经验回归方程=+t中斜率、截距的最小二乘估计公式、样本相关系数公式分别为==,=- ,
r=;
参考数据:=232.56.
章末检测试卷三(第八章)
1.C
2.D [根据散点图中各样本点条状分布越均匀,同时保持残差平方和越小,其线性回归模型的拟合效果就越好,由此知丁同学的线性回归模型的拟合效果最好.]
3.C [由题意知,经验回归方程是=95+0.06x,两艘轮船吨位相差1 000吨,所以船员平均人数的差值是0.06×1 000=60.]
4.C [由公式
χ2=中所有值变为原来的2倍,
得(χ2)′==2χ2,故χ2也变为原来的2倍.]
5.D [只有χ2≥6.635=x0.01时才能在犯错误的概率不超过1%的前提下,认为该电视栏目是否优秀与改革有关系,而即使χ2≥6.635也只是对“该电视栏目是否优秀与改革有关系”这个论断成立的可能性大小的推论,与是否有99%的人等无关.]
6.B [由表格数据知
==5,
==50,
∴=-6.5=50-32.5=17.5,
∴经验回归方程为=6.5x+17.5,
∴6.5×9+17.5=76(元),即当工作时间为9小时时,工资大约为76元.]
7.C [列联表如下.
卡塔尔世界杯 性别 合计
男生 女生
关注 50 10 60
不关注 30 20 50
合计 80 30 110
则χ2=≈7.486.
对于A,χ2≈7.486>3.841=x0.05,依据小概率值α=0.05的独立性检验,认为学生对卡塔尔世界杯的关注与性别有关,故A错误;
对于B,男生不关注卡塔尔世界杯的比例为=,女生关注卡塔尔世界杯的比例为=,且>,则男生不关注卡塔尔世界杯的比例高于女生关注卡塔尔世界杯的比例,故B错误;
对于C,D,χ2≈7.486>6.635=x0.01,则在犯错误的概率不超过1%的前提下,可以认为学生对卡塔尔世界杯的关注与性别有关,故C正确,D错误.]
8.D [设=t,
则==4,
==8,
代入得=8-×4=-,
则=-,
当x=16时,=×4-=8,
则第16天的残差为9-8=1.]
9.BC [由题意知成绩优秀的学生数是30,成绩非优秀的学生数是75,
所以c=20,b=45,故A错误,B正确;
根据列联表中的数据,得到χ2=
≈6.109>3.841=x0.05,而χ2≈6.109<6.635=x0.01,
因此在犯错误的概率不超过0.05的前提下认为“成绩与班级有关系”,故C正确,D错误.]
10.ACD [由=-0.7x+10.3得=-0.7<0,所以x,y呈负相关,故A正确;
当x=11时,y的预测值为2.6,故C正确;
由==9,
得=-0.7×9+10.3=4.
故经验回归直线过(9,4),故D正确;
因为=4,所以=4,解得m=5,故B错误.]
11.AC [对于选项A,该学校男生对食堂服务满意的概率的估计值为=,故A正确;
对于选项B,该学校女生对食堂服务满意的概率的估计值为=>,故B错误;
因为χ2≈4.762>3.841=x0.05,且χ2≈4.762<6.635=x0.01,所以依据小概率值α=0.05的独立性检验,可以认为男、女生对该食堂服务的评价有差异,故C正确,D错误.]
12.ACD [将=3,代入=1.5x+0.5,得=5,因为重新求得的回归直线l的斜率为1.2,故变量x与y具有正相关关系,故A正确;
设新的数据所有的横坐标的平均值为1,则(n-2)1=n-(1.2+4.8)=3n-6=3(n-2),故 1=3,
设纵坐标的平均值为1,则(n-2)1=n-(2.2+7.8)=5n-10=5(n-2), 1=5,设新的经验回归方程为=1.2x+,把(3,5)代入得5=1.2×3+,=1.4,故新的经验回归方程为=1.2x+1.4,故C正确;
因为1.5>1.2,所以y的增长速度变慢,故B错误;
把x=2代入新的经验回归方程,得=3.8,3.75-3.8=-0.05,故D正确.]
13.262
解析 由题意,得=4,
=(1 028+a),
代入=4x+242,
可得(1 028+a)=4×4+242,解得a=262.
14.1
解析 由ei=0,知yi=i,
即yi-i=0,
故R2=1-=1-0=1.
15.4.844 0.05
解析 χ2=≈4.844>3.841=x0.05,根据小概率值α=0.05的独立性检验,可知认为主修统计专业与性别有关,此推断犯错误的概率不超过0.05.
16.8 24.047
解析 由2×2列联表得
a=49,b=54,c=25,d=46.
∴b-d=54-46=8.
χ2=
≈24.047.
17.解 补充列联表如表:
性别 心理障碍 合计
有 没有
女生 10 20 30
男生 10 70 80
合计 20 90 110
零假设为H0:心理障碍与性别无关.
根据列联表中的数据,经计算得
χ2=
≈6.366>3.841=x0.05.
根据小概率值α=0.05的独立性检验,可以认为H0不成立.即认为心理障碍与性别有关,此判断犯错误的概率不超过0.05.
18.解 (1)由所给数据计算得
=×(1+2+3+4+5+6+7)=4,
=×(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
(ti-)2=9+4+1+0+1+4+9=28,
(ti-)(yi-)
=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
===0.5,
=-=4.3-0.5×4=2.3,
故所求经验回归方程为=0.5t+2.3.
(2)由(1)知,=0.5>0,故2016年至2022年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2024年的年份代号t=9代入(1)中的经验回归方程,
得=0.5×9+2.3=6.8(千元),
故预测该地区2024年农村居民家庭人均纯收入为6.8千元.
19.解 (1)由散点图知各点呈非线性递增趋势,
所以y=c+d作为经验回归模型比较合适.
(2)由wi=,
则===68,
由=6.8,=563,
得=- =563-68×6.8=100.6,
所以=100.6+68.
(3)根据(2)的结果知,年利润z的预测值=0.2(100.6+68)-x=20.12+13.6-()2=-(-6.8)2+66.36,
所以当=6.8,即x=46.24时,年利润的预测值最大.
20.解 (1)1 000人中,步数不超过8千步的有20+60+170+200=450(人),步数超过8千步的有550人,用比例分配的分层随机抽样方法,抽取的人数中不超过8千步的有90人,超过8千步的有110人,
故40岁以上且日行步数不超过8千步的有40人,40岁以上且日行步数超过8千步的有60人,
40岁以下(含40岁)日行步数超过8千步的有50人,合计40岁以下(含40岁)的人数为100人,
补全的列联表如下.
年龄 日行步数 合计
不超过8千步 超过8千步
40岁以上 40 60 100
40岁以下(含40岁) 50 50 100
合计 90 110 200
(2)零假设为H0:日行步数与居民年龄无关,
计算得χ2
=≈2.02<3.841=x0.05,
根据小概率值α=0.05的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,
即认为日行步数与居民年龄无关.
21.解 (1)200名学生中得分超过85分的人数为150,其中男生人数为100,女生人数为50,
因此样本中男生人数为×6=4,
样本中女生人数为×6=2,
设“这3名学生中至少有一名女生”为事件A,则
P(A)=1-=1-=.
(2)零假设为H0:了解安全知识的程度与性别无关,计算可得χ2==
≈11.11>10.828=x0.001,
根据小概率值α=0.001的独立性检验,
我们认为了解安全知识的程度与性别有关,
此推断犯错误的概率不大于0.001.
22.解 (1)若用y=a+bx作为经验回归模型,
则==3,(xi-)2=(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2=10,
所以样本相关系数r1==,
若用y=a+bln x作为经验回归模型,
样本相关系数r2=
=,
比较r与r,
r==,
r==,
因为r
=i=×4.79=0.958,
=i=×62=12.4,
=-=12.4-12×0.958=0.904,
则y关于x的经验回归方程为=0.904+12ln x.
