人教版九年级数学下册的26章26.2实际问题与反比例函数训练题(含答案)
文档属性
| 名称 | 人教版九年级数学下册的26章26.2实际问题与反比例函数训练题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 136.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-05 17:29:03 | ||
图片预览


文档简介
人教版九年级数学下册的26章26.2实际问题与反比例函数训练题(含答案)
一.选择题(共5小题)
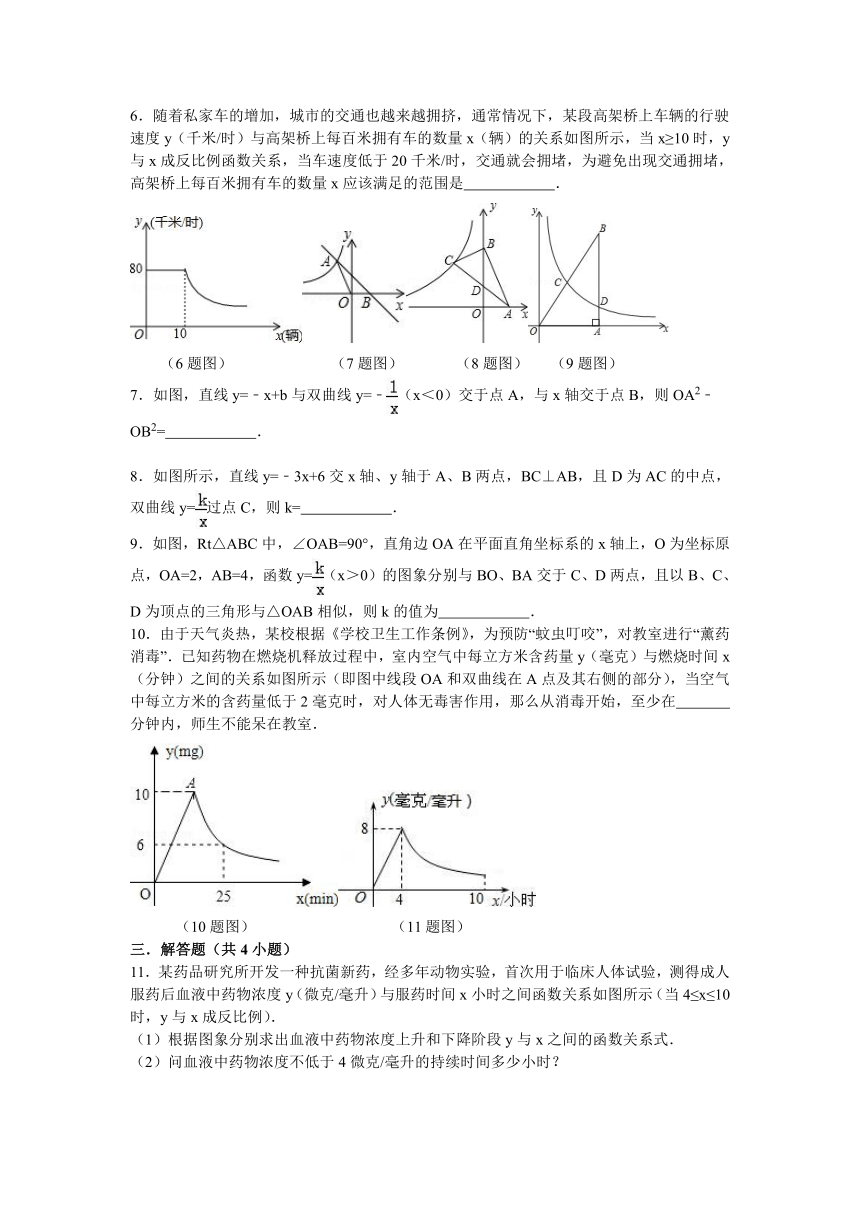
1.如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
A. B. C. D.
2.已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A.B.C.D.
3.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A.B.C.D.
4.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的( )
A.7:00 B. 7:10 C. 7:25 D. 7:35
(4题图) (5题图)
5.如图,在直角坐标系中,有菱形OABC,A点的坐标是(10,0),双曲线经过点C,且OB AC=160,则k的值为( )
A.40 B. 48 C. 64 D. 80
二.填空题(共5小题)
6.随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .
(6题图) (7题图) (8题图) (9题图)
7.如图,直线y=﹣x+b与双曲线y=﹣(x<0)交于点A,与x轴交于点B,则OA2﹣OB2= .
8.如图所示,直线y=﹣3x+6交x轴、y轴于A、B两点,BC⊥AB,且D为AC的中点,双曲线y=过点C,则k= .
9.如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为 .
10.由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在 分钟内,师生不能呆在教室.
(10题图) (11题图)
三.解答题(共4小题)
11.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
12.如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
13.如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于12℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
14.直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线(x<0)交于点A(﹣1,n).
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由.
人教版九年级数学下册的26章26.2实际问题与反比例函数训练题参考答案
一.选择题(共5小题)
1.A.2.C.3.C.4.B.5.B.
二.填空题(共5小题)
6. 0<x<40 .7. 2 8. ﹣ .9. 10. 75
三.解答题(共4小题)
11. 解:(1)当0≤x≤4时,设直线解析式为:y=kx,
将(4,8)代入得:8=4k,解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设直反比例函数解析式为:y=,
将(4,8)代入得:8=,解得:a=32,
故反比例函数解析式为:y=;
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
12.
解:(1)把A(﹣2,0)代入y=ax+1中,求得a=,
∴y=x+1,
由PC=2,把y=2代入y=x+1中,得x=2,即P(2,2),
把P代入y=得:k=4,
则双曲线解析式为y=;
(2)设Q(a,b),
∵Q(a,b)在y=上,∴b=,
当△QCH∽△BAO时,可得=,即=,∴a﹣2=2b,即a﹣2=,
解得:a=4或a=﹣2(舍去),
∴Q(4,1);
当△QCH∽△ABO时,可得=,即=,
整理得:2a﹣4=,
解得:a=1+或a=1﹣(舍),
∴Q(1+,2﹣2).
综上,Q(4,1)或Q(1+,2﹣2).
13.解:(1)设加热停止后反比例函数表达式为y=,
∵y=过(12,14),得k1=12×14=168,则y=;
当y=28时,28=,得x=6.
设加热过程中一次函数表达式y=k2x+b,
由图象知y=k2x+b过点(0,4)与(6,28),
∴,解得,
∴y=4x+4,此时x的范围是0≤x≤6.
y=此时x的范围是x>6;
(2)当y=12时,由y=4x+4,得x=2.
由y=,得x=14,
所以对该材料进行特殊处理所用的时间为14﹣2=12(分钟).
14.解:(1)∵直线y=x+b与x轴交于点C(4,0),
∴把点C(4,0)代入y=x+b得:b=﹣4,
∴直线的解析式是:y=x﹣4;
∵直线也过A点,
∴把A点代入y=x﹣4得到:n=﹣5
∴A(﹣1,﹣5),
把将A点代入(x<0)得:m=5,
∴双曲线的解析式是:y=;
(2)过点O作OM⊥AC于点M,
∵B点经过y轴,∴x=0,∴0﹣4=y,∴y=﹣4,∴B(0,﹣4),
AO==,
∵OC=OB=4,∴△OCB是等腰三角形,∴∠OBC=∠OCB=45°,
∴在△OMB中 sin45°==,
∴OM=2,
∴在△AOM中,sin∠OAB===;
(3)存在;
过点A作AN⊥y轴,垂足为点N,
则AN=1,BN=1,
则AB==,
∵OB=OC=4,
∴BC==4,
∠OBC=∠OCB=45°,
∴∠OBA=∠BCD=135°,
∴△OBA∽△BCD或△OBA∽△DCB,
∴=或=,
∴=或=,
∴CD=2或CD=16,
∵点C(4,0),
∴点D的坐标是(20,0)或(6,0).
一.选择题(共5小题)
1.如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
A. B. C. D.
2.已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A.B.C.D.
3.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A.B.C.D.
4.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的( )
A.7:00 B. 7:10 C. 7:25 D. 7:35
(4题图) (5题图)
5.如图,在直角坐标系中,有菱形OABC,A点的坐标是(10,0),双曲线经过点C,且OB AC=160,则k的值为( )
A.40 B. 48 C. 64 D. 80
二.填空题(共5小题)
6.随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .
(6题图) (7题图) (8题图) (9题图)
7.如图,直线y=﹣x+b与双曲线y=﹣(x<0)交于点A,与x轴交于点B,则OA2﹣OB2= .
8.如图所示,直线y=﹣3x+6交x轴、y轴于A、B两点,BC⊥AB,且D为AC的中点,双曲线y=过点C,则k= .
9.如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为 .
10.由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在 分钟内,师生不能呆在教室.
(10题图) (11题图)
三.解答题(共4小题)
11.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
12.如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
13.如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于12℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
14.直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线(x<0)交于点A(﹣1,n).
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由.
人教版九年级数学下册的26章26.2实际问题与反比例函数训练题参考答案
一.选择题(共5小题)
1.A.2.C.3.C.4.B.5.B.
二.填空题(共5小题)
6. 0<x<40 .7. 2 8. ﹣ .9. 10. 75
三.解答题(共4小题)
11. 解:(1)当0≤x≤4时,设直线解析式为:y=kx,
将(4,8)代入得:8=4k,解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设直反比例函数解析式为:y=,
将(4,8)代入得:8=,解得:a=32,
故反比例函数解析式为:y=;
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
12.
解:(1)把A(﹣2,0)代入y=ax+1中,求得a=,
∴y=x+1,
由PC=2,把y=2代入y=x+1中,得x=2,即P(2,2),
把P代入y=得:k=4,
则双曲线解析式为y=;
(2)设Q(a,b),
∵Q(a,b)在y=上,∴b=,
当△QCH∽△BAO时,可得=,即=,∴a﹣2=2b,即a﹣2=,
解得:a=4或a=﹣2(舍去),
∴Q(4,1);
当△QCH∽△ABO时,可得=,即=,
整理得:2a﹣4=,
解得:a=1+或a=1﹣(舍),
∴Q(1+,2﹣2).
综上,Q(4,1)或Q(1+,2﹣2).
13.解:(1)设加热停止后反比例函数表达式为y=,
∵y=过(12,14),得k1=12×14=168,则y=;
当y=28时,28=,得x=6.
设加热过程中一次函数表达式y=k2x+b,
由图象知y=k2x+b过点(0,4)与(6,28),
∴,解得,
∴y=4x+4,此时x的范围是0≤x≤6.
y=此时x的范围是x>6;
(2)当y=12时,由y=4x+4,得x=2.
由y=,得x=14,
所以对该材料进行特殊处理所用的时间为14﹣2=12(分钟).
14.解:(1)∵直线y=x+b与x轴交于点C(4,0),
∴把点C(4,0)代入y=x+b得:b=﹣4,
∴直线的解析式是:y=x﹣4;
∵直线也过A点,
∴把A点代入y=x﹣4得到:n=﹣5
∴A(﹣1,﹣5),
把将A点代入(x<0)得:m=5,
∴双曲线的解析式是:y=;
(2)过点O作OM⊥AC于点M,
∵B点经过y轴,∴x=0,∴0﹣4=y,∴y=﹣4,∴B(0,﹣4),
AO==,
∵OC=OB=4,∴△OCB是等腰三角形,∴∠OBC=∠OCB=45°,
∴在△OMB中 sin45°==,
∴OM=2,
∴在△AOM中,sin∠OAB===;
(3)存在;
过点A作AN⊥y轴,垂足为点N,
则AN=1,BN=1,
则AB==,
∵OB=OC=4,
∴BC==4,
∠OBC=∠OCB=45°,
∴∠OBA=∠BCD=135°,
∴△OBA∽△BCD或△OBA∽△DCB,
∴=或=,
∴=或=,
∴CD=2或CD=16,
∵点C(4,0),
∴点D的坐标是(20,0)或(6,0).
