7.5 正态分布 学案(含答案)-2024春高中数学选择性必修3(人教版)
文档属性
| 名称 | 7.5 正态分布 学案(含答案)-2024春高中数学选择性必修3(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 159.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 15:47:41 | ||
图片预览



文档简介
7.5 正态分布
[学习目标]
1.利用实际问题的频率分布直方图,了解正态曲线的特点及正态曲线所表示的意义.
2.了解变量落在区间[ μ-σ,μ+σ ],[ μ-2σ,μ+2σ ],[ μ-3σ,μ+3σ ]内的概率大小.
3.会用正态分布去解决实际问题.
一、正态曲线及其特征
问题1 下列随机变量哪个是离散型随机变量:
(1)掷一枚骰子一次,用X表示所得点数;
(2)白炽灯的使用时间.
问题2 教材P74例2的高尔顿板试验中,随着重复次数的增加,频率分布直方图的形状会越来越像一条钟形曲线,那么这条曲线是否存在函数解析式呢?
知识梳理
1.我们称f(x)=______________________,x∈R,其中μ∈R,σ>0为参数,为______________________,称它的图象为正态密度曲线,简称______________.
2.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为____________.特别地,当μ=0,σ=1时,称随机变量X服从________________.
3.若X~N(μ,σ2),则E(X)=μ,D(X)=σ2.
4.正态曲线的特点:
(1)非负性:对 x∈R,f(x)>0,它的图象在x轴的________.
(2)定值性:曲线与x轴之间的区域的面积为________.
(3)对称性:曲线是单峰的,它关于直线________对称.
(4)最大值:曲线在______处达到峰值.
(5)当|x|无限增大时,曲线无限接近____轴.
(6)当________一定时,正态曲线的位置由μ确定,正态曲线随着________的变化而沿x轴平移,如图①.
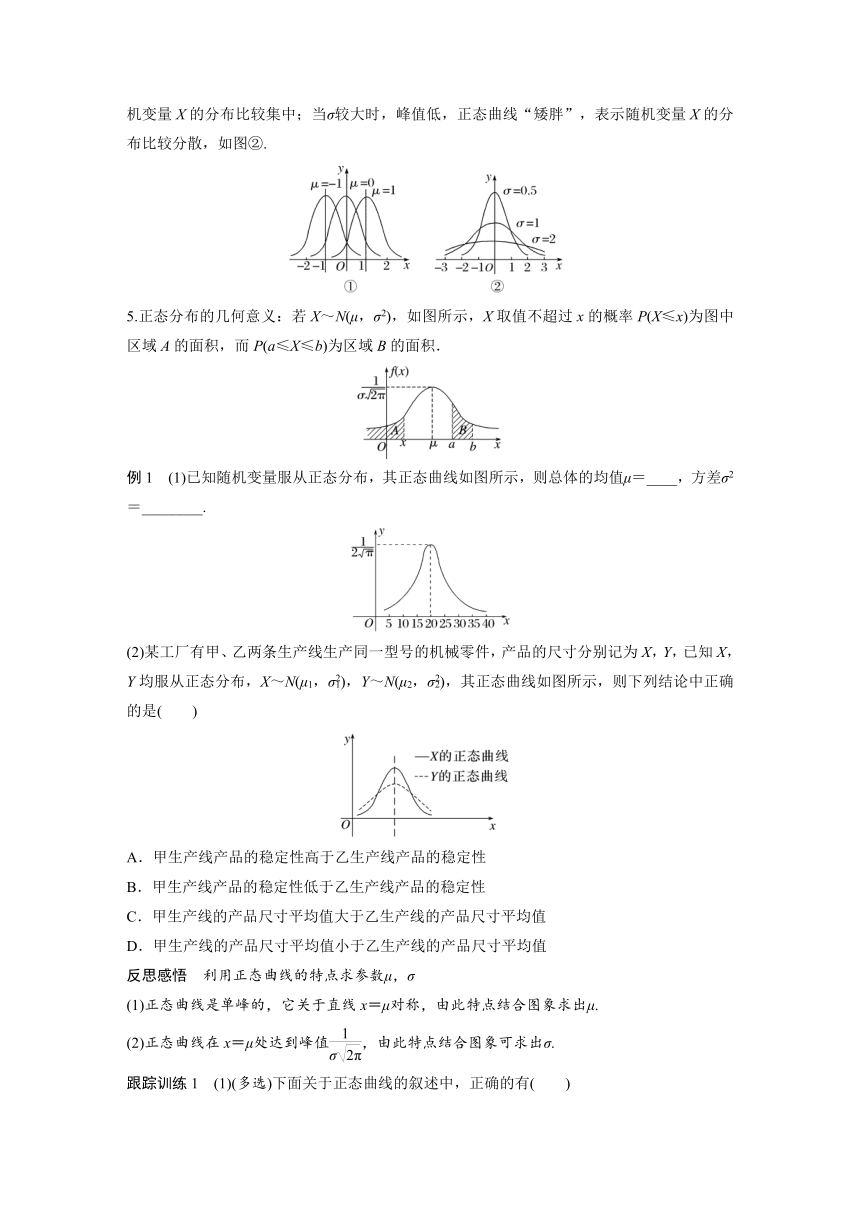
(7)当μ一定时,正态曲线的形状由σ确定,当σ较小时,峰值高,正态曲线“瘦高”,表示随机变量X的分布比较集中;当σ较大时,峰值低,正态曲线“矮胖”,表示随机变量X的分布比较分散,如图②.
5.正态分布的几何意义:若X~N(μ,σ2),如图所示,X取值不超过x的概率P(X≤x)为图中区域A的面积,而P(a≤X≤b)为区域B的面积.
例1 (1)已知随机变量服从正态分布,其正态曲线如图所示,则总体的均值μ=____,方差σ2=________.
(2)某工厂有甲、乙两条生产线生产同一型号的机械零件,产品的尺寸分别记为X,Y,已知X,Y均服从正态分布,X~N(μ1,σ),Y~N(μ2,σ),其正态曲线如图所示,则下列结论中正确的是( )
A.甲生产线产品的稳定性高于乙生产线产品的稳定性
B.甲生产线产品的稳定性低于乙生产线产品的稳定性
C.甲生产线的产品尺寸平均值大于乙生产线的产品尺寸平均值
D.甲生产线的产品尺寸平均值小于乙生产线的产品尺寸平均值
反思感悟 利用正态曲线的特点求参数μ,σ
(1)正态曲线是单峰的,它关于直线x=μ对称,由此特点结合图象求出μ.
(2)正态曲线在x=μ处达到峰值,由此特点结合图象可求出σ.
跟踪训练1 (1)(多选)下面关于正态曲线的叙述中,正确的有( )
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
(2)(多选)甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ),N(μ2,σ),其正态密度函数f(x)=,x∈R的正态曲线如图所示,则下列说法正确的是( )
A.甲类水果的平均质量μ1=0.4 kg
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数σ2=1.99
二、利用正态分布的性质求概率
知识梳理
正态总体在三个特殊区间内取值的概率值
P(μ-σ≤X≤μ+σ)≈________;
P(μ-2σ≤X≤μ+2σ)≈________;
P(μ-3σ≤X≤μ+3σ)≈________.
例2 设ξ~N(1,22),试求:
(1)P(-1≤ξ≤3);(2)P(3≤ξ≤5).
延伸探究 若本例条件不变,求P(ξ>5).
反思感悟 利用正态分布求概率的两个方法
(1)对称法:由于正态曲线是关于直线x=μ对称的,且概率的和为1,故关于直线x=μ对称的区间概率相等.如:
①P(X<a)=1-P(X≥a);
②P(X<μ-a)=P(X>μ+a).
(2)“3σ”法:利用X落在区间[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]内的概率分别是0.682 7,0.954 5,0.997 3求解.
跟踪训练2 (1)已知随机变量ξ服从正态分布N(1,σ2),且P(ξ<2)=0.6,则P(0<ξ<2)等于( )
A.0.4 B.0.3 C.0.2 D.0.1
(2)随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=0.2,P(2<ξ<6)=0.6,则μ等于( )
A.3 B.4 C.5 D.6
三、正态分布的应用
例3 (1)现实世界中的很多随机变量遵循正态分布.例如反复测量某一个物理量,其测量误差X通常被认为服从正态分布.若某物理量做n次测量,最后结果的误差Xn ~N,则为使|Xn|>的概率控制在0.045 5及以下,至少要测量的次数为(附:若随机变量X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)( )
A.32 B.64 C.128 D.256
(2)某厂生产的圆柱形零件的外直径X(单位:cm)服从正态分布N(4,0.52).质检人员从该厂生产的1 000件零件中随机抽查1件,测得它的外直径为5.7 cm,试问:该厂生产的这批零件是否合格?
反思感悟 解题时,应当注意零件尺寸应落在[μ-3σ,μ+3σ]之内,否则可以认为该批产品不合格.判断的根据是小概率事件在一次试验中几乎是不可能发生的,而一旦发生了,就可以认为这批产品不合格.
跟踪训练3 已知某平台某次促销活动期间,某小区居民网上购物的消费金额(单位:元)近似服从正态分布N(600,10 000),则该小区800名居民中,网购金额超过800元的人数大约为(附:若随机变量X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)( )
A.16 B.18 C.20 D.25
1.知识清单:
(1)正态曲线及其特征.
(2)利用正态分布的性质求概率.
(3)正态分布的应用.
2.方法归纳:转化化归、数形结合.
3.常见误区:概率区间转化不等价.
1.设有一正态总体,它的正态曲线是函数f(x)的图象,且f(x)=,则这个正态总体的均值与标准差分别是( )
A.10与8 B.10与2
C.8与10 D.2与10
2.某学校共1 000人参加数学测验,考试成绩ξ近似服从正态分布N(100,σ2),若P(80≤ξ≤100)=0.45,则估计成绩在120分以上的学生人数为( )
A.25 B.50 C.75 D.100
3.已知随机变量X服从正态分布N(10,22),则D(3X-1)等于( )
A.6 B.11 C.12 D.36
4.如果ξ~N(μ,σ2),且P(ξ>3)=P(ξ<1)成立,则μ=________.
7.5 正态分布
问题1 (1)是,(2)不是.
问题2 存在.
知识梳理
1. 正态密度函数
正态曲线
2.X~N(μ,σ2) 标准正态分布
4.(1)上方 (2)1 (3)x=μ (4)x=μ
(5)x (6)σ μ
例1 (1)20 2
解析 从给出的正态曲线可知,该正态曲线关于直线x=20对称,最大值是,所以=,解得σ=,因此总体的均值μ=20,方差σ2=()2=2.
(2)A [由图知甲、乙两条生产线的平均值相等,甲的正态曲线较瘦高,所以甲生产线产品的稳定性高于乙生产线产品的稳定性.]
跟踪训练1 (1)ABD [只有C错误,因为当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,总体分布越集中;σ越大,曲线越“矮胖”,总体分布越分散.]
(2)ABC [由图象可知甲图象关于直线x=0.4对称,乙图象关于直线x=0.8对称,
所以μ1=0.4,μ2=0.8,μ1<μ2,故A,C正确;
因为甲图象比乙图象更“瘦高”,所以甲类水果的质量比乙类水果的质量更集中于平均值左右,故B正确;
因为乙图象的最大值为1.99,
即=1.99,σ2≠1.99,故D错误.]
知识梳理
0.682 7 0.954 5 0.997 3
例2 解 ∵ξ~N(1,22),
∴μ=1,σ=2,
(1)P(-1≤ξ≤3)=P(1-2≤ξ≤1+2)
=P(μ-σ≤ξ≤μ+σ)≈0.682 7.
(2)∵P(3≤ξ≤5)=P(-3≤ξ≤-1),
∴P(3≤ξ≤5)=[P(-3≤ξ≤5)-P(-1≤ξ≤3)]
=[P(1-4≤ξ≤1+4)-
P(1-2≤ξ≤1+2)]
=[P(μ-2σ≤ξ≤μ+2σ)-
P(μ-σ≤ξ≤μ+σ)]
≈×(0.954 5-0.682 7)
=0.135 9.
延伸探究 解 P(ξ>5)=
P(ξ<-3)=[1-P(-3≤ξ≤5)]
=[1-P(1-4≤ξ≤1+4)]
=[1-P(μ-2σ≤ξ≤μ+2σ)]
≈×(1-0.954 5)=0.022 75.
跟踪训练2 (1)C [由已知可得曲线关于直线x=1对称,
P(ξ<2)=0.6,
所以P(ξ≥2)=P(ξ≤0)=0.4,
故P(0<ξ<2)=1-0.4-0.4=0.2.]
(2)B [∵P(ξ<2)=0.2,
P(2<ξ<6)=0.6,
∴P(ξ>6)=1-0.2-0.6=0.2,
即P(ξ<2)=P(ξ>6),
∴μ==4.]
例3 (1)C [根据题意,
P≤0.045 5 P=P≥1-0.045 5=0.954 5,
而μ=0,
则P(-2σ≤Xn≤2σ)≈0.954 5,
所以2σ≤ σ=≤ n≥128.]
(2)解 由于外直径X~N(4,0.52),
则X在[4-3×0.5,4+3×0.5]之内取值的概率为0.997 3,在[2.5,5.5]之外取值的概率为0.002 7,
而5.7 [2.5,5.5],这说明在一次试验中,出现了几乎不可能发生的小概率事件,据此可以认为这批零件是不合格的.
跟踪训练3 B [∵小区居民网上购物的消费金额(单位:元)近似服从正态分布N(600,
10 000),
∴P=
≈=0.022 75,
∴该小区800名居民中,网购金额超过800元的人数大约为0.022 75×800=18.2≈18.]
随堂演练
1.B [由正态密度函数的定义可知,总体的均值μ=10,方差σ2=4,
即σ=2.]
2.B [由已知可得,μ=100,
所以P(ξ≥100)=0.5.
又P(80≤ξ≤100)=0.45,根据正态分布的对称性可得P(100≤ξ≤120)=0.45,
所以P(ξ>120)
=P(ξ≥100)-P(100≤ξ≤120)
=0.5-0.45=0.05.
所以,可估计成绩在120分以上的学生人数为1 000×0.05=50.]
3.D [因为随机变量X服从正态分布N(10,22),
所以D(X)=22=4,
所以D(3X-1)
=32D(X)=9×4=36.]
4.2
解析 因为ξ~N(μ,σ2),故正态曲线关于直线x=μ对称,又P(ξ<1)=P(ξ>3),从而μ==2,即μ的值为2.
[学习目标]
1.利用实际问题的频率分布直方图,了解正态曲线的特点及正态曲线所表示的意义.
2.了解变量落在区间[ μ-σ,μ+σ ],[ μ-2σ,μ+2σ ],[ μ-3σ,μ+3σ ]内的概率大小.
3.会用正态分布去解决实际问题.
一、正态曲线及其特征
问题1 下列随机变量哪个是离散型随机变量:
(1)掷一枚骰子一次,用X表示所得点数;
(2)白炽灯的使用时间.
问题2 教材P74例2的高尔顿板试验中,随着重复次数的增加,频率分布直方图的形状会越来越像一条钟形曲线,那么这条曲线是否存在函数解析式呢?
知识梳理
1.我们称f(x)=______________________,x∈R,其中μ∈R,σ>0为参数,为______________________,称它的图象为正态密度曲线,简称______________.
2.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为____________.特别地,当μ=0,σ=1时,称随机变量X服从________________.
3.若X~N(μ,σ2),则E(X)=μ,D(X)=σ2.
4.正态曲线的特点:
(1)非负性:对 x∈R,f(x)>0,它的图象在x轴的________.
(2)定值性:曲线与x轴之间的区域的面积为________.
(3)对称性:曲线是单峰的,它关于直线________对称.
(4)最大值:曲线在______处达到峰值.
(5)当|x|无限增大时,曲线无限接近____轴.
(6)当________一定时,正态曲线的位置由μ确定,正态曲线随着________的变化而沿x轴平移,如图①.
(7)当μ一定时,正态曲线的形状由σ确定,当σ较小时,峰值高,正态曲线“瘦高”,表示随机变量X的分布比较集中;当σ较大时,峰值低,正态曲线“矮胖”,表示随机变量X的分布比较分散,如图②.
5.正态分布的几何意义:若X~N(μ,σ2),如图所示,X取值不超过x的概率P(X≤x)为图中区域A的面积,而P(a≤X≤b)为区域B的面积.
例1 (1)已知随机变量服从正态分布,其正态曲线如图所示,则总体的均值μ=____,方差σ2=________.
(2)某工厂有甲、乙两条生产线生产同一型号的机械零件,产品的尺寸分别记为X,Y,已知X,Y均服从正态分布,X~N(μ1,σ),Y~N(μ2,σ),其正态曲线如图所示,则下列结论中正确的是( )
A.甲生产线产品的稳定性高于乙生产线产品的稳定性
B.甲生产线产品的稳定性低于乙生产线产品的稳定性
C.甲生产线的产品尺寸平均值大于乙生产线的产品尺寸平均值
D.甲生产线的产品尺寸平均值小于乙生产线的产品尺寸平均值
反思感悟 利用正态曲线的特点求参数μ,σ
(1)正态曲线是单峰的,它关于直线x=μ对称,由此特点结合图象求出μ.
(2)正态曲线在x=μ处达到峰值,由此特点结合图象可求出σ.
跟踪训练1 (1)(多选)下面关于正态曲线的叙述中,正确的有( )
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
(2)(多选)甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ),N(μ2,σ),其正态密度函数f(x)=,x∈R的正态曲线如图所示,则下列说法正确的是( )
A.甲类水果的平均质量μ1=0.4 kg
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数σ2=1.99
二、利用正态分布的性质求概率
知识梳理
正态总体在三个特殊区间内取值的概率值
P(μ-σ≤X≤μ+σ)≈________;
P(μ-2σ≤X≤μ+2σ)≈________;
P(μ-3σ≤X≤μ+3σ)≈________.
例2 设ξ~N(1,22),试求:
(1)P(-1≤ξ≤3);(2)P(3≤ξ≤5).
延伸探究 若本例条件不变,求P(ξ>5).
反思感悟 利用正态分布求概率的两个方法
(1)对称法:由于正态曲线是关于直线x=μ对称的,且概率的和为1,故关于直线x=μ对称的区间概率相等.如:
①P(X<a)=1-P(X≥a);
②P(X<μ-a)=P(X>μ+a).
(2)“3σ”法:利用X落在区间[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]内的概率分别是0.682 7,0.954 5,0.997 3求解.
跟踪训练2 (1)已知随机变量ξ服从正态分布N(1,σ2),且P(ξ<2)=0.6,则P(0<ξ<2)等于( )
A.0.4 B.0.3 C.0.2 D.0.1
(2)随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=0.2,P(2<ξ<6)=0.6,则μ等于( )
A.3 B.4 C.5 D.6
三、正态分布的应用
例3 (1)现实世界中的很多随机变量遵循正态分布.例如反复测量某一个物理量,其测量误差X通常被认为服从正态分布.若某物理量做n次测量,最后结果的误差Xn ~N,则为使|Xn|>的概率控制在0.045 5及以下,至少要测量的次数为(附:若随机变量X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)( )
A.32 B.64 C.128 D.256
(2)某厂生产的圆柱形零件的外直径X(单位:cm)服从正态分布N(4,0.52).质检人员从该厂生产的1 000件零件中随机抽查1件,测得它的外直径为5.7 cm,试问:该厂生产的这批零件是否合格?
反思感悟 解题时,应当注意零件尺寸应落在[μ-3σ,μ+3σ]之内,否则可以认为该批产品不合格.判断的根据是小概率事件在一次试验中几乎是不可能发生的,而一旦发生了,就可以认为这批产品不合格.
跟踪训练3 已知某平台某次促销活动期间,某小区居民网上购物的消费金额(单位:元)近似服从正态分布N(600,10 000),则该小区800名居民中,网购金额超过800元的人数大约为(附:若随机变量X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)( )
A.16 B.18 C.20 D.25
1.知识清单:
(1)正态曲线及其特征.
(2)利用正态分布的性质求概率.
(3)正态分布的应用.
2.方法归纳:转化化归、数形结合.
3.常见误区:概率区间转化不等价.
1.设有一正态总体,它的正态曲线是函数f(x)的图象,且f(x)=,则这个正态总体的均值与标准差分别是( )
A.10与8 B.10与2
C.8与10 D.2与10
2.某学校共1 000人参加数学测验,考试成绩ξ近似服从正态分布N(100,σ2),若P(80≤ξ≤100)=0.45,则估计成绩在120分以上的学生人数为( )
A.25 B.50 C.75 D.100
3.已知随机变量X服从正态分布N(10,22),则D(3X-1)等于( )
A.6 B.11 C.12 D.36
4.如果ξ~N(μ,σ2),且P(ξ>3)=P(ξ<1)成立,则μ=________.
7.5 正态分布
问题1 (1)是,(2)不是.
问题2 存在.
知识梳理
1. 正态密度函数
正态曲线
2.X~N(μ,σ2) 标准正态分布
4.(1)上方 (2)1 (3)x=μ (4)x=μ
(5)x (6)σ μ
例1 (1)20 2
解析 从给出的正态曲线可知,该正态曲线关于直线x=20对称,最大值是,所以=,解得σ=,因此总体的均值μ=20,方差σ2=()2=2.
(2)A [由图知甲、乙两条生产线的平均值相等,甲的正态曲线较瘦高,所以甲生产线产品的稳定性高于乙生产线产品的稳定性.]
跟踪训练1 (1)ABD [只有C错误,因为当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,总体分布越集中;σ越大,曲线越“矮胖”,总体分布越分散.]
(2)ABC [由图象可知甲图象关于直线x=0.4对称,乙图象关于直线x=0.8对称,
所以μ1=0.4,μ2=0.8,μ1<μ2,故A,C正确;
因为甲图象比乙图象更“瘦高”,所以甲类水果的质量比乙类水果的质量更集中于平均值左右,故B正确;
因为乙图象的最大值为1.99,
即=1.99,σ2≠1.99,故D错误.]
知识梳理
0.682 7 0.954 5 0.997 3
例2 解 ∵ξ~N(1,22),
∴μ=1,σ=2,
(1)P(-1≤ξ≤3)=P(1-2≤ξ≤1+2)
=P(μ-σ≤ξ≤μ+σ)≈0.682 7.
(2)∵P(3≤ξ≤5)=P(-3≤ξ≤-1),
∴P(3≤ξ≤5)=[P(-3≤ξ≤5)-P(-1≤ξ≤3)]
=[P(1-4≤ξ≤1+4)-
P(1-2≤ξ≤1+2)]
=[P(μ-2σ≤ξ≤μ+2σ)-
P(μ-σ≤ξ≤μ+σ)]
≈×(0.954 5-0.682 7)
=0.135 9.
延伸探究 解 P(ξ>5)=
P(ξ<-3)=[1-P(-3≤ξ≤5)]
=[1-P(1-4≤ξ≤1+4)]
=[1-P(μ-2σ≤ξ≤μ+2σ)]
≈×(1-0.954 5)=0.022 75.
跟踪训练2 (1)C [由已知可得曲线关于直线x=1对称,
P(ξ<2)=0.6,
所以P(ξ≥2)=P(ξ≤0)=0.4,
故P(0<ξ<2)=1-0.4-0.4=0.2.]
(2)B [∵P(ξ<2)=0.2,
P(2<ξ<6)=0.6,
∴P(ξ>6)=1-0.2-0.6=0.2,
即P(ξ<2)=P(ξ>6),
∴μ==4.]
例3 (1)C [根据题意,
P≤0.045 5 P=P≥1-0.045 5=0.954 5,
而μ=0,
则P(-2σ≤Xn≤2σ)≈0.954 5,
所以2σ≤ σ=≤ n≥128.]
(2)解 由于外直径X~N(4,0.52),
则X在[4-3×0.5,4+3×0.5]之内取值的概率为0.997 3,在[2.5,5.5]之外取值的概率为0.002 7,
而5.7 [2.5,5.5],这说明在一次试验中,出现了几乎不可能发生的小概率事件,据此可以认为这批零件是不合格的.
跟踪训练3 B [∵小区居民网上购物的消费金额(单位:元)近似服从正态分布N(600,
10 000),
∴P=
≈=0.022 75,
∴该小区800名居民中,网购金额超过800元的人数大约为0.022 75×800=18.2≈18.]
随堂演练
1.B [由正态密度函数的定义可知,总体的均值μ=10,方差σ2=4,
即σ=2.]
2.B [由已知可得,μ=100,
所以P(ξ≥100)=0.5.
又P(80≤ξ≤100)=0.45,根据正态分布的对称性可得P(100≤ξ≤120)=0.45,
所以P(ξ>120)
=P(ξ≥100)-P(100≤ξ≤120)
=0.5-0.45=0.05.
所以,可估计成绩在120分以上的学生人数为1 000×0.05=50.]
3.D [因为随机变量X服从正态分布N(10,22),
所以D(X)=22=4,
所以D(3X-1)
=32D(X)=9×4=36.]
4.2
解析 因为ξ~N(μ,σ2),故正态曲线关于直线x=μ对称,又P(ξ<1)=P(ξ>3),从而μ==2,即μ的值为2.
