2.9.1有理数的乘法法则 课件

课件22张PPT。有理数的乘法 在小学里我们已经学习了正有理数和零的
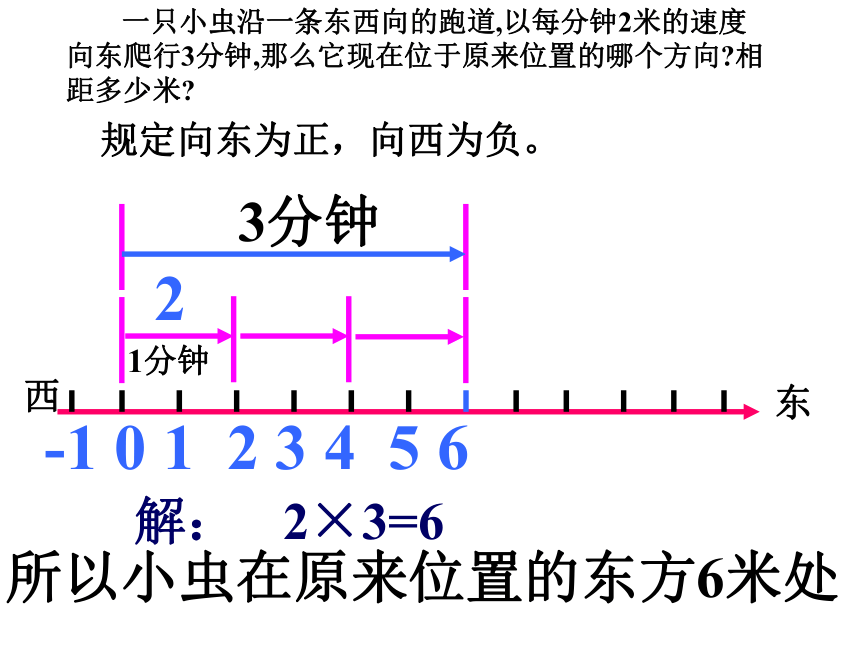
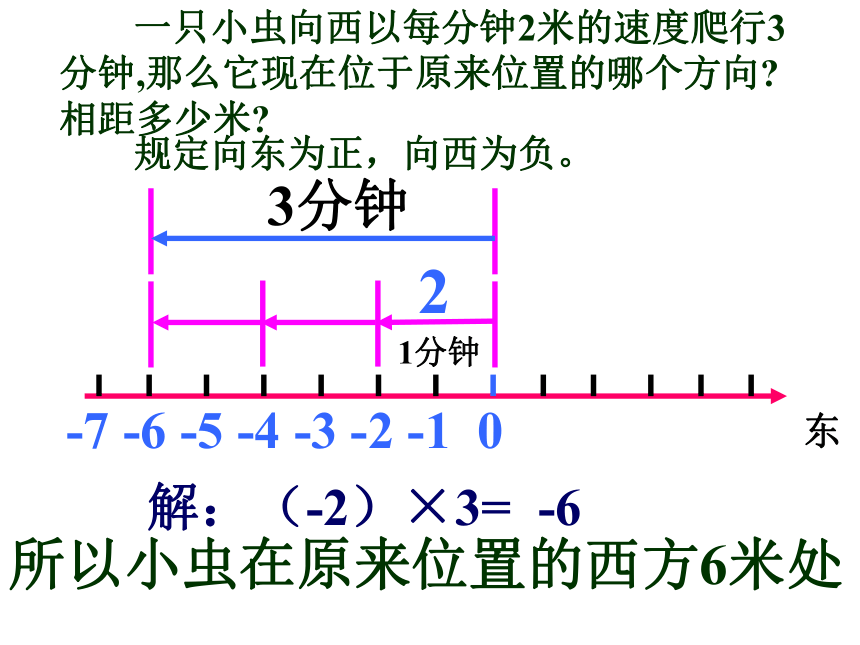
乘法运算,请同学们计算下列各题： 3× 3 0 × 6 2 × 0 一只小虫沿一条东西向的 跑道,以每分钟2米的速度向东爬行3分钟,那么它现在位于原来位置的哪个方向?相距多少米?问题1-1 0 1 2 3 4 5 6 23分钟解： 2×3=6所以小虫在原来位置的东方6米处1分钟东西 一只小虫沿一条东西向的跑道,以每分钟2米的速度向东爬行3分钟,那么它现在位于原来位置的哪个方向?相距多少米?规定向东为正，向西为负。问题2 一只小虫向西以每分钟2米的速度爬行3分钟,那么它现在位于原来位置的哪个方向?相距多少米?解：（-2）×3= -6所以小虫在原来位置的西方6米处 一只小虫向西以每分钟2米的速度爬行3分钟,那么它现在位于原来位置的哪个方向?相距多少米?
23分钟1分钟东规定向东为正，向西为负。-7 -6 -5 -4 -3 -2 -1 0 2 × 3= 6（-2）× 3= -6积的相反数积是原来的 两数相乘，把一个因数换成它的相反数，所得的积是原来的积的相反数。 相反数
一个因数换成2×3= 62×( -3)=做一做-6-2×（-3）=6几个式子综合如下：
（1） 2×3=6
（2）（-2） × 3 = -6
（3） 2×（-3） = -6
（4）（-2）×（-3）=6 积的符号与两因数符号的关系：正数乘正数积为———数，正负数乘正数积为———数，负正数乘负数积为———数，负负数乘负数积为———数。正积的绝对值与两因数绝对值的关系：积的绝对值等于各因数绝对值的______。积任意数与0相乘，得数是多少？思考：并把绝对值相乘。两数相乘，同号得正，异号得负，有理数乘法法则：
两数相乘，同号得正，异号得负，
并把绝对值相乘。
任何数与零相乘，都得零。例如 （-7） ×（- 4）（同号两数相乘）（-7）×（- 4）= +（ ）（得正）7×4 = 28（把绝对值相乘）∴（-7）×（-4）=28又如：（-7）×4（异号两数相乘）（-7）×4= -（　）（得负）7×4=28（把绝对值相乘）∴（-7）×4=-28口答：确定下列两数积的符号。
（1） （－4） × （2） （－ ） ×（－9）
（3） 5×（－3） （ 3） 0.5×0.7
（4） （4）=－（ ）=+（ ）=－（ ）=+（ ）=－（ ）=－（ ）例1:计算:(1) (-5) ×(-6)解: (1)(-5) ×(-6)=+( )=30得正，同号两数相乘把绝对值相乘5×6=－（ ）=－异号两数相乘得负，把绝对值相乘下面计算有误吗？计算：解：原式==例2练习：
(1)（-8）×（-7） (2)（- ）×9 (3) （ -1 ）× 例3： 口算：
(1) 3×（-1）； (2) （-5）×（-1）；
(3) ×（-1）； (4) 0×（-1）；
(5) （-6）×1； (6) 2×1；
(7) 0×1； (8) 1×（-1）
做完这题，你能发现什么规律？
一个数与1相乘，积是什么？
一个数与（-1）相乘呢？(1)一个数同+1相乘，得原数。(2)一个数同-1相乘，得原数的相反数。(1) 6?(? 9) (2) (? 6)?(? 9)
(3) (? 6)?9 (4) (? 6)?1
(5) (?6)?(?1) (6) 6?(?1)
(7) (? 6)?0 (8) 0?(?6)
(9) (?6)? 0.25 (10) (?0.5)?(?8)＝? 54＝ ? 54 ＝54＝6 ＝ ? 6＝ ? 6＝0 ＝0＝?1.5＝41.口答题学以致用：2.如果a×b=0，则这两个数 （ ）A 都等于0， B 有一个等于0，另一个不等于0；
C 至少有一个等于0 D 互为相反数3.已知-3a是一个负数，则 （ ）A a>0 B a<0 C a≥0 D a≤0CA4.两个有理数和为0，积为负，则这两个数的关系是 （ ）A 两个数均为0， B 两个数中一个为0
C 两数互为相反数， D 两数互为相反数，但不为0。D (用“＞”或“＜”号连接)：
(1)如果a＜0，b＜0，那么ab_______0；
(2)如果a＜0，b>0，那么ab_______0；
(3)如果a＞0时，那么a_______2a；
(4)如果a＜0时，那么a_______2a。＞＜＜＞5.填空题：6.若ab﹥0，则必有 （ ）
A、a﹥0 ,b﹥0 B 、a﹤0 ,b﹤0
C 、a﹥0 ,b﹤0 D 、a,b 同号
D小结：1.有理数乘法法则：两数相乘,同号得正,异号得负,并把绝对值相乘；
任何数与零相乘,都得零。2.如何进行两个有理数的乘法运算：先确定积的符号，再把绝对值相乘，当有一个因数为零时，积为零。