第18章 平行四边形单元测试卷(含解析)
文档属性
| 名称 | 第18章 平行四边形单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 21:14:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第18章平行四边形单元测试卷
时间100分钟 满分120分
姓名 班级 考号
一、选择题(每小题3分,共36分)
1.在平行四边形中,的角平分线把边分成长度为4和5的两条线段,则平行四边形的周长为( )
A.13或14 B.26或28 C.13 D.无法确定
2.如图 ABCD中,点O是对角线、的交点,过点O的直线分别交、于点M、N,若的面积为3,的面积为5,则 ABCD的面积是( )
A.16 B.24 C.32 D.40
3.如图,四边形中,,,E、F是对角线上的两点,如果再添加一个条件,使,则添加的条件不能是( )
A. B. C. D.
4.以点O、A、B、C为顶点的平行四边形放置在平面直角坐标系中,其中点O为坐标原点.若点C的坐标是,点A的坐标是,则点B的坐标是( )
A.或 B.或
C.或或 D.或或
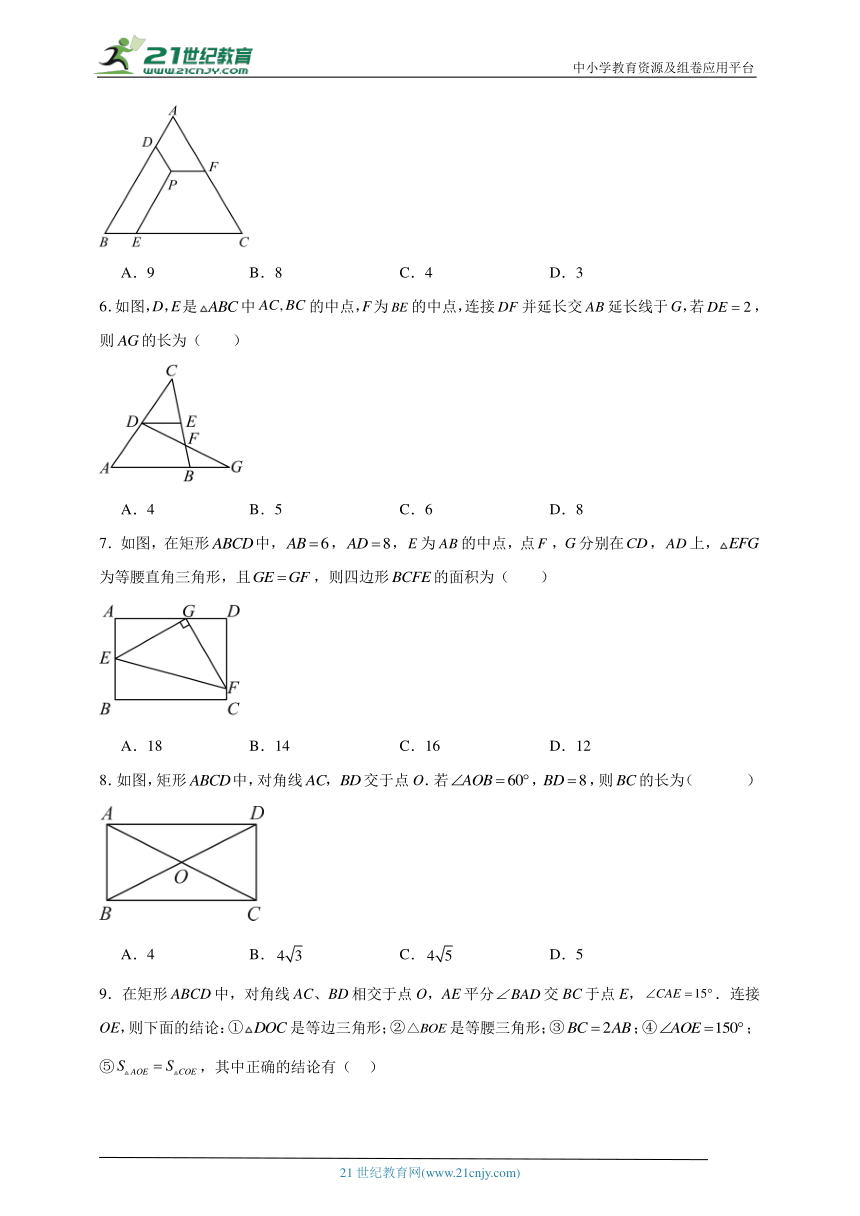
5.如图,在周长为9的等边三角形的内部有一点P,过点P作,,分别交三边于点D,E,F,则等于( )
A.9 B.8 C.4 D.3
6.如图,D,E是中的中点,F为的中点,连接并延长交延长线于G,若,则的长为( )
A.4 B.5 C.6 D.8
7.如图,在矩形中,,,为的中点,点,G分别在,上,为等腰直角三角形,且,则四边形的面积为( )
A.18 B.14 C.16 D.12
8.如图,矩形中,对角线交于点O.若,,则的长为( )
A.4 B. C. D.5
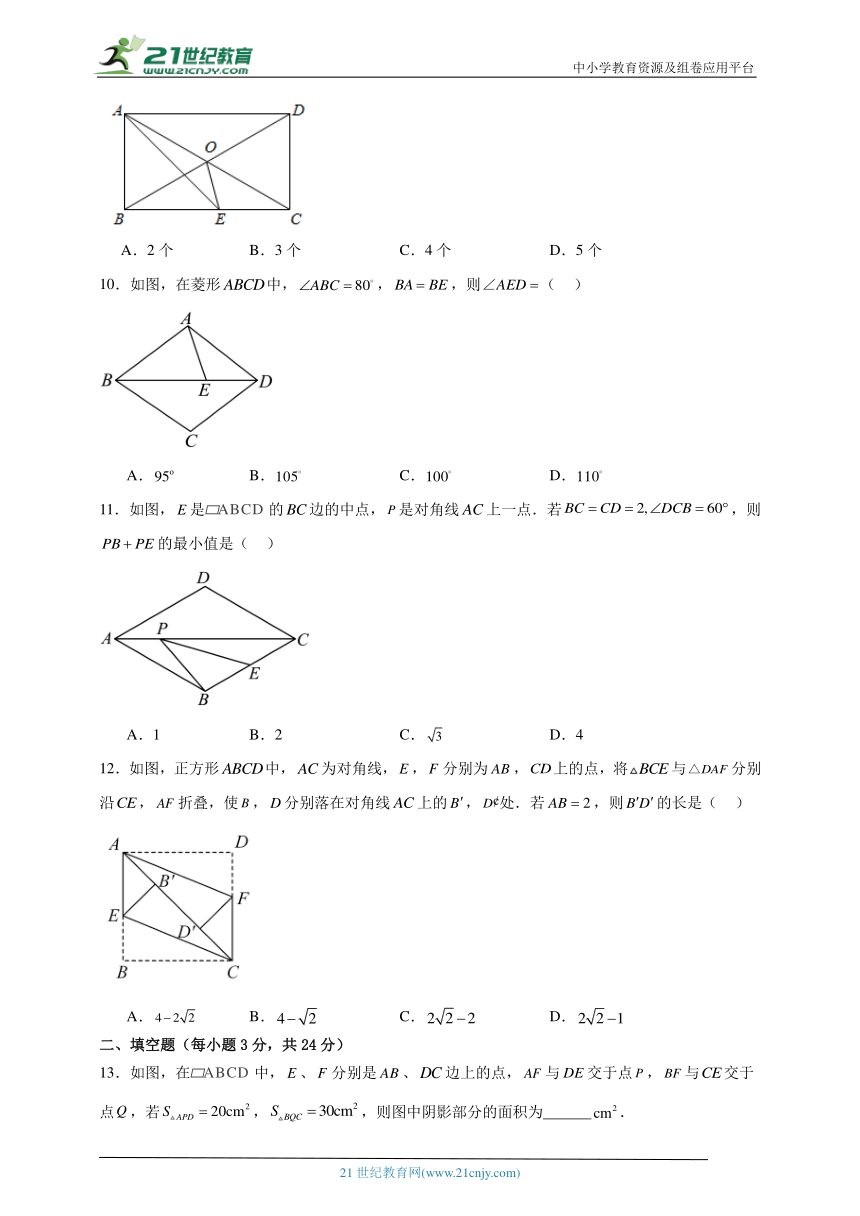
9.在矩形ABCD中,对角线AC、BD相交于点O,AE平分交BC于点E,.连接OE,则下面的结论:①是等边三角形;②是等腰三角形;③;④;⑤,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
10.如图,在菱形中,,,则( )
A. B. C. D.
11.如图,是 ABCD的边的中点,是对角线上一点.若,则的最小值是( )
A.1 B.2 C. D.4
12.如图,正方形中,为对角线,,分别为,上的点,将与分别沿,折叠,使,分别落在对角线上的,处.若,则的长是( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13.如图,在 ABCD中,、分别是、边上的点,与交于点,与交于点,若,,则图中阴影部分的面积为 .
14.如图,在等腰直角三角形中,,,的面积等于35,点P在上,点Q在上,,上有一动点M,若要使最小,则该最小值是 .
15.如图,在矩形中,的平分线交于点于点,连接并延长交于点,连接交于点,下列结论:
;
;
;
.
其中正确的有 填序号
16.如图,矩形的边厘米,厘米,在直角梯形中,厘米,厘米,厘米,点,,,在同一直线上,且厘米,矩形从点开始以厘米/秒的速度沿直线向右运动,同时点从点出发沿的路线,以厘米/秒的速度运动,到点停止.当点共运动 秒时,点与点相距厘米.
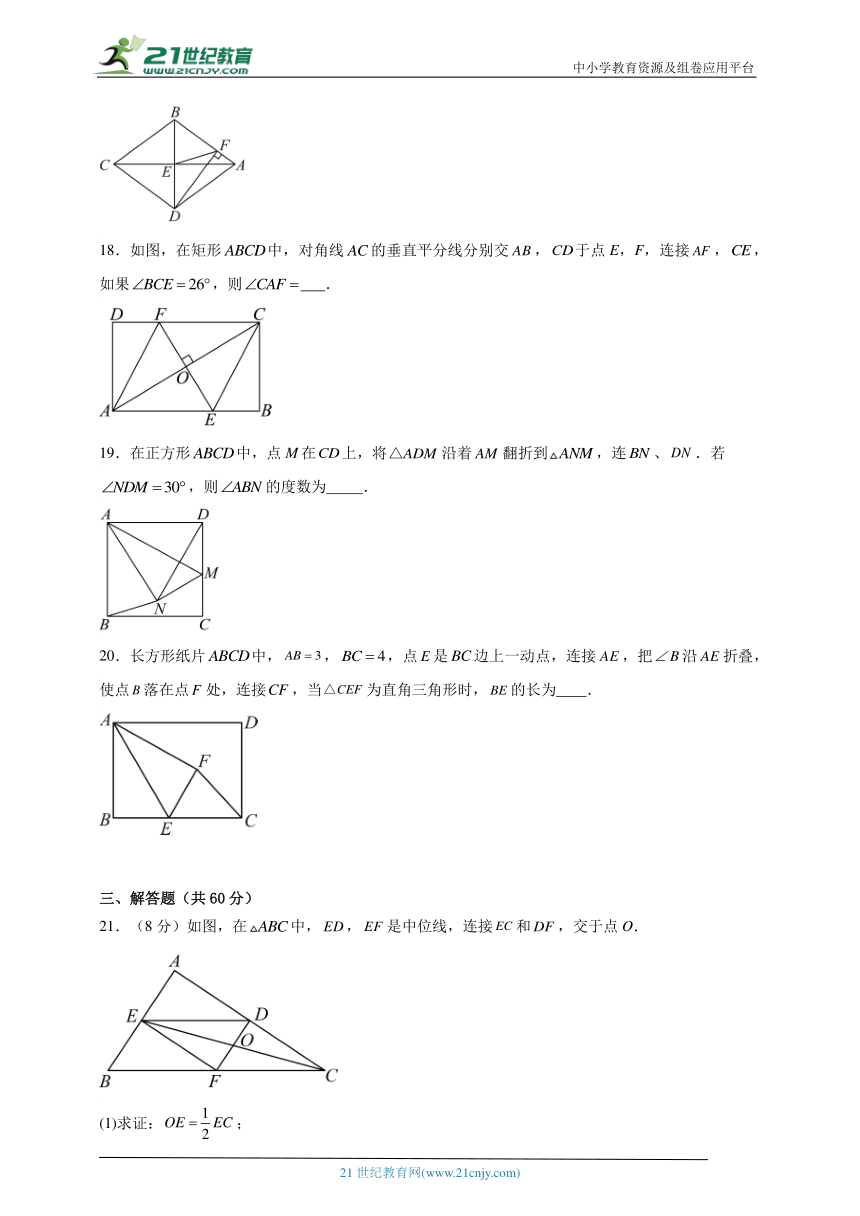
17.如图,四边形是菱形,交于点交于点,连接,若,则 .
18.如图,在矩形中,对角线的垂直平分线分别交,于点E,F,连接,,如果,则 .
19.在正方形中,点M在上,将沿着翻折到,连、.若,则的度数为 .
20.长方形纸片中,,,点是边上一动点,连接,把沿折叠,使点落在点处,连接,当为直角三角形时,的长为 .
三、解答题(共60分)
21.(8分)如图,在中,,是中位线,连接和,交于点O.
(1)求证:;
(2)若,求的长.
22.(8分)如图,已知在 ABCD中,点分别是边的中点,过点的直线交的延长线于点,连接.
(1)求证:四边形是平行四边形;
(2)求证:.
23.(8分)如图,四边形中,对角线,相交于点,,,且.
(1)求证:四边形是矩形;
(2)若,求的度数.
24.(10分)如图,在四边形中,,,,,,点从点出发,沿射线以每秒2个单位长度的速度向右运动,同时点从点出发,沿方向以每秒1个单位长度的速度向点运动.当点到达点时,点停止运动,设点运动时间为秒.
(1)当运动停止时,求线段的长;
(2)当t为何值时,四边形为矩形,求出t的值和矩形的面积;
(3)在运动的过程中,是否存在某一时刻,使以,,,为顶点的四边形为平行四边形?若存在,请求出的值,若不存在,请说明理由.
25.(8分)在中,,D是的中点,过点A作,且,连接.
(1)证明:四边形是菱形;
(2)若,求菱形的面积.
26.(8分)如图,在 ABCD中,E是的中点,连接并延长交的延长线于点F.
(1)求证:.
(2)连接,.
①当时,的形状是________.
②若,当________时,四边形是菱形.
27.(10分)“玩转数学”实践活动,是一种非常有效的学习方式,我们一起来动手、动脑玩转数学吧.如图①,折一折:将正方形纸片折叠,使边,都落在对角线上,展开得折痕,,连接.
(1)_______°;
转一转:如图②,将图①中的绕点A旋转,使它的两边分别交边,于点P,Q,连接.
(2)猜想线段、、之间的数量关系,并说明理由;
(3)若正方形的边长为6,,求的长.
第18章平行四边形单元测试卷参考答案
1.B[提示:设的平分线交于点E,
∵四边形是平行四边形,
∴,
∴,
∵,
∴,
∴,
当,时,如图1,
则,,
∴;
当,时,如图2,
则,,
∴,
∴平行四边形的周长为26或28,
故选:B.]
2.C[提示:过点O做EF垂直于BC,交BC于点F,交AD于点E
∵在 ABCD中,AO=OC,
∴
∵
∴
∴
∵
∴
∴
∵,
∴
故选:C.]
3.A[提示:∵四边形是平行四边形,
;
又,
,
,
;
;
∴四边形是平行四边形,故B正确;
∵四边形是平行四边形,
;
又,
,
,
,
;
;
;
∴四边形是平行四边形,故C正确;
∵四边形是平行四边形,
;
又∵,
,
;
;
;
∴四边形是平行四边形,故D正确;
添加后,不能得出,进而得不出四边形平行四边形,
故选:A.]
4.D[提示:如图:当为对角线时,点的坐标为,即;
当为边时,点的坐标为,即;点的坐标为,即.
故选D.]
5.D[提示:延长交于点,延长交于点,
∵,,,
四边形、四边形均为平行四边形,
∴.
为等边三角形,
∴,
∴,
∴是等边三角形,
同理可得是等边三角形,
∴,
∴,
∵的周长为9,
∴
,
故选D.]
6.C[解:∵D,E是中的中点,
∴,即,
∴,
又∵F为的中点,
∴,
在与中,,
∴,
∴,
∴,
故选:C.]
7.C[提示:为等腰直角三角形,,,
,
四边形是矩形,
,
,
,
在和中,
,
,
,,
,,为的中点,
,,
,
,
故选:C.]
8.B[提示:矩形中,对角线交于点O,,
,,
,
是等边三角形,
,
,
故选B.]
9.B[提示:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB ∠CAE=45° 15°=30°,
∴∠BAO=90° 30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,
又∵ AB=BE,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
在Rt△ABC中
∵∠ACB=30°
∴BC=AB,故③错误;
∵∠OBE=∠ABC ∠ABO=90° 60°=30°=∠ACB,
∴∠BOE=(180° 30°)=75°,
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴,故⑤正确;
故选:B.]
10.D[提示:∵四边形是菱形,
∴平分,
∴,
∵,
∴,
∴,
故选:.]
11.C[提示:∵四边形是平行四边形,,
∴ ABCD是菱形,
连接,交于O,连接交于P,
由菱形的对角线互相垂直平分,可得B、D关于对称,则,
∴,
即就是的最小值.
∵四边形是菱形,
∴,,
∴是等边三角形,
∵,
∴.
在中,.
即的最小值为.
故选:C.]
12.A[提示:∵正方形中,为对角线,,
∴,,
设,
∵将与分别沿,折叠,使,分别落在对角线上的,处.
∴,,,
∴, 是等腰直角三角形,
∴,
在中,,
即,
∴,
∴,
解得,
即的长是,
故选:A]
13.50[提示:如图,连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFC-S△QFC =S△BCF-S△QFC,
即S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△APD,
∵S△APD=20cm2,S△BQC=30cm2,
∴S四边形EPFQ= S△APD + S△BQC =50cm2,
故答案为:50.]
14.[提示:,,,
,,
,
作点P关于的对称点N,则,
,
当M,N,Q三点共线时,取最小值,最小值为,
如下图所示,与交点即为M,
由题意知垂直平分,
,,
,
,,
四边形是平行四边形,
,
即的最小值为.
故答案为:.]
15.[提示:四边形是矩形,
,
平分,
,
是等腰直角三角形,
,
,
,故正确,
在和中,
,
,
,
,
,
,
,故正确;
,
,
,
,
,
,
,
,故正确;
连接.
,
,
,
,
,
,
,
,故正确.
故答案为:.]
16.、或[提示:如图,∵厘米,矩形从点开始以厘米/秒的速度沿直线向右运动,同时点从点出发沿的路线,以厘米/秒的速度运动,
∴开始运动秒后,点运动到点,
过点作于,则四边形和四边形以及四边形都是矩形,
∴(厘米),
设再过秒,则,
当点与点相距厘米时,即厘米,
∵厘米,,
∴,
解得或,
∴点共运动了秒或秒时,点与点相距厘米;
开始运动秒后,点运动到点,此时,厘米,如图,
设再过秒后,点与点相距厘米,
∵,
∴即,
解得(舍去)或,
∴点共运动了秒时,点与点相距厘米,
故答案为:、或.]
17.9.6/[提示:如图,取中点,连接,
四边形是菱形,
,,
是的中位线,
,,
又,
,
在的垂直平分线上,
,
,,
,
,
,
,
故答案为:9.6.]
18.[提示:∵四边形是矩形,
∴,,,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∵垂直平分线段,
∴,
∴四边形是菱形,
∵,
∴,
∴,
∴,
故答案为:.]
19./75度[提示:如图,设与相交于点E,
由翻折得,,
∵四边形是正方形,,
∴,
∴,
∴,
∴,
∴,
∴.]
20.或[提示:如图,当共线时,,
∵四边形是矩形,
∴,
∴,
由折叠性质可知:,,
∴,
设,则,
在中,由勾股定理得:,
即:,解得:,
如图,当落在上时,,
此时四边形为正方形,
∴,
综上可知:的长为或,
故答案为:或.]
21.(1)证明:∵,是的中位线,
∴,,
∴四边形是平行四边形
∵对角线、相交于点O,
∴;
(2)解:∵、是平行四边形的对角线,,
∴,
∵,是的中位线,
∴D,F分别是的中点
∴,
即.
22.(1)证明:∵四边形是平行四边形,
∴,即,
∵点分别是边的中点,
∴,即,
∴四边形是平行四边形;
(2)∵四边形是平行四边形,
∴,
∵,
∴四边形是平行四边形,
∴,
∵四边形是平行四边形,
∴,
又∵点是边的中点,
∴,
∴.
23.(1)证明:,,
四边形是平行四边形,
,
,
,
,
平行四边形是矩形;
(2)解:四边形是矩形,
,,
,
,
,
,
,
,
.
24.解;(1)由题意知,运动停止时,P点运动时间为秒,
∴,
∴,
∴运动停止时,的长为;
(2)如图,过D作于E,
∴四边形为矩形,
∴,,
∴,
∴,
由题可得,,若四边形为矩形,
则,即,
解得:,则,
∴;
(3)由题意知,分两种情况求解:
①当为平行四边形的边,则在点左侧,,,
∵,
∴,
解得;
②当为平行四边形的对角线,在点右侧,,,
∵,
∴,
解得 ,
综上所述,存在,当或时,以,,,为顶点的四边形为平行四边形.
25.(1)证明:∵,D是的中点,,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∴平行四边形是菱形.
(2)解:∵平行四边形是菱形,
∴,
∵D是的中点,
∴,
∴.
26.(1)证明:∵四边形是平行四边形,
,
∴,
∵E是的中点,
∴,
在△ADE和中,
,
∴,
∴.
(2)①等腰三角形,
连接AC,如图:
∵,
∴ ABCD是矩形,
∴,
∵,,
∴四边形是平行四边形.
∴.
∴.
∴△BDF是等腰三角形.
②55,
∵ ABCD是菱形,
∴,.
∴.
∵,
∴.
∴,
故答案为:等腰三角形;55.
27.(1)解:由翻折的性质可知,,
正方形纸片,
,
,
,
,
;
(2)解:延长到,使,
正方形纸片,
,
△ABT≌△ADQ(SAS),
,
,
,
,
,
△PAT≌△PAQ(SAS)
,
;
(3)解:,
,
,
,
,
在中,,
即,
解得或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第18章平行四边形单元测试卷
时间100分钟 满分120分
姓名 班级 考号
一、选择题(每小题3分,共36分)
1.在平行四边形中,的角平分线把边分成长度为4和5的两条线段,则平行四边形的周长为( )
A.13或14 B.26或28 C.13 D.无法确定
2.如图 ABCD中,点O是对角线、的交点,过点O的直线分别交、于点M、N,若的面积为3,的面积为5,则 ABCD的面积是( )
A.16 B.24 C.32 D.40
3.如图,四边形中,,,E、F是对角线上的两点,如果再添加一个条件,使,则添加的条件不能是( )
A. B. C. D.
4.以点O、A、B、C为顶点的平行四边形放置在平面直角坐标系中,其中点O为坐标原点.若点C的坐标是,点A的坐标是,则点B的坐标是( )
A.或 B.或
C.或或 D.或或
5.如图,在周长为9的等边三角形的内部有一点P,过点P作,,分别交三边于点D,E,F,则等于( )
A.9 B.8 C.4 D.3
6.如图,D,E是中的中点,F为的中点,连接并延长交延长线于G,若,则的长为( )
A.4 B.5 C.6 D.8
7.如图,在矩形中,,,为的中点,点,G分别在,上,为等腰直角三角形,且,则四边形的面积为( )
A.18 B.14 C.16 D.12
8.如图,矩形中,对角线交于点O.若,,则的长为( )
A.4 B. C. D.5
9.在矩形ABCD中,对角线AC、BD相交于点O,AE平分交BC于点E,.连接OE,则下面的结论:①是等边三角形;②是等腰三角形;③;④;⑤,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
10.如图,在菱形中,,,则( )
A. B. C. D.
11.如图,是 ABCD的边的中点,是对角线上一点.若,则的最小值是( )
A.1 B.2 C. D.4
12.如图,正方形中,为对角线,,分别为,上的点,将与分别沿,折叠,使,分别落在对角线上的,处.若,则的长是( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13.如图,在 ABCD中,、分别是、边上的点,与交于点,与交于点,若,,则图中阴影部分的面积为 .
14.如图,在等腰直角三角形中,,,的面积等于35,点P在上,点Q在上,,上有一动点M,若要使最小,则该最小值是 .
15.如图,在矩形中,的平分线交于点于点,连接并延长交于点,连接交于点,下列结论:
;
;
;
.
其中正确的有 填序号
16.如图,矩形的边厘米,厘米,在直角梯形中,厘米,厘米,厘米,点,,,在同一直线上,且厘米,矩形从点开始以厘米/秒的速度沿直线向右运动,同时点从点出发沿的路线,以厘米/秒的速度运动,到点停止.当点共运动 秒时,点与点相距厘米.
17.如图,四边形是菱形,交于点交于点,连接,若,则 .
18.如图,在矩形中,对角线的垂直平分线分别交,于点E,F,连接,,如果,则 .
19.在正方形中,点M在上,将沿着翻折到,连、.若,则的度数为 .
20.长方形纸片中,,,点是边上一动点,连接,把沿折叠,使点落在点处,连接,当为直角三角形时,的长为 .
三、解答题(共60分)
21.(8分)如图,在中,,是中位线,连接和,交于点O.
(1)求证:;
(2)若,求的长.
22.(8分)如图,已知在 ABCD中,点分别是边的中点,过点的直线交的延长线于点,连接.
(1)求证:四边形是平行四边形;
(2)求证:.
23.(8分)如图,四边形中,对角线,相交于点,,,且.
(1)求证:四边形是矩形;
(2)若,求的度数.
24.(10分)如图,在四边形中,,,,,,点从点出发,沿射线以每秒2个单位长度的速度向右运动,同时点从点出发,沿方向以每秒1个单位长度的速度向点运动.当点到达点时,点停止运动,设点运动时间为秒.
(1)当运动停止时,求线段的长;
(2)当t为何值时,四边形为矩形,求出t的值和矩形的面积;
(3)在运动的过程中,是否存在某一时刻,使以,,,为顶点的四边形为平行四边形?若存在,请求出的值,若不存在,请说明理由.
25.(8分)在中,,D是的中点,过点A作,且,连接.
(1)证明:四边形是菱形;
(2)若,求菱形的面积.
26.(8分)如图,在 ABCD中,E是的中点,连接并延长交的延长线于点F.
(1)求证:.
(2)连接,.
①当时,的形状是________.
②若,当________时,四边形是菱形.
27.(10分)“玩转数学”实践活动,是一种非常有效的学习方式,我们一起来动手、动脑玩转数学吧.如图①,折一折:将正方形纸片折叠,使边,都落在对角线上,展开得折痕,,连接.
(1)_______°;
转一转:如图②,将图①中的绕点A旋转,使它的两边分别交边,于点P,Q,连接.
(2)猜想线段、、之间的数量关系,并说明理由;
(3)若正方形的边长为6,,求的长.
第18章平行四边形单元测试卷参考答案
1.B[提示:设的平分线交于点E,
∵四边形是平行四边形,
∴,
∴,
∵,
∴,
∴,
当,时,如图1,
则,,
∴;
当,时,如图2,
则,,
∴,
∴平行四边形的周长为26或28,
故选:B.]
2.C[提示:过点O做EF垂直于BC,交BC于点F,交AD于点E
∵在 ABCD中,AO=OC,
∴
∵
∴
∴
∵
∴
∴
∵,
∴
故选:C.]
3.A[提示:∵四边形是平行四边形,
;
又,
,
,
;
;
∴四边形是平行四边形,故B正确;
∵四边形是平行四边形,
;
又,
,
,
,
;
;
;
∴四边形是平行四边形,故C正确;
∵四边形是平行四边形,
;
又∵,
,
;
;
;
∴四边形是平行四边形,故D正确;
添加后,不能得出,进而得不出四边形平行四边形,
故选:A.]
4.D[提示:如图:当为对角线时,点的坐标为,即;
当为边时,点的坐标为,即;点的坐标为,即.
故选D.]
5.D[提示:延长交于点,延长交于点,
∵,,,
四边形、四边形均为平行四边形,
∴.
为等边三角形,
∴,
∴,
∴是等边三角形,
同理可得是等边三角形,
∴,
∴,
∵的周长为9,
∴
,
故选D.]
6.C[解:∵D,E是中的中点,
∴,即,
∴,
又∵F为的中点,
∴,
在与中,,
∴,
∴,
∴,
故选:C.]
7.C[提示:为等腰直角三角形,,,
,
四边形是矩形,
,
,
,
在和中,
,
,
,,
,,为的中点,
,,
,
,
故选:C.]
8.B[提示:矩形中,对角线交于点O,,
,,
,
是等边三角形,
,
,
故选B.]
9.B[提示:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB ∠CAE=45° 15°=30°,
∴∠BAO=90° 30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,
又∵ AB=BE,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
在Rt△ABC中
∵∠ACB=30°
∴BC=AB,故③错误;
∵∠OBE=∠ABC ∠ABO=90° 60°=30°=∠ACB,
∴∠BOE=(180° 30°)=75°,
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴,故⑤正确;
故选:B.]
10.D[提示:∵四边形是菱形,
∴平分,
∴,
∵,
∴,
∴,
故选:.]
11.C[提示:∵四边形是平行四边形,,
∴ ABCD是菱形,
连接,交于O,连接交于P,
由菱形的对角线互相垂直平分,可得B、D关于对称,则,
∴,
即就是的最小值.
∵四边形是菱形,
∴,,
∴是等边三角形,
∵,
∴.
在中,.
即的最小值为.
故选:C.]
12.A[提示:∵正方形中,为对角线,,
∴,,
设,
∵将与分别沿,折叠,使,分别落在对角线上的,处.
∴,,,
∴, 是等腰直角三角形,
∴,
在中,,
即,
∴,
∴,
解得,
即的长是,
故选:A]
13.50[提示:如图,连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFC-S△QFC =S△BCF-S△QFC,
即S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△APD,
∵S△APD=20cm2,S△BQC=30cm2,
∴S四边形EPFQ= S△APD + S△BQC =50cm2,
故答案为:50.]
14.[提示:,,,
,,
,
作点P关于的对称点N,则,
,
当M,N,Q三点共线时,取最小值,最小值为,
如下图所示,与交点即为M,
由题意知垂直平分,
,,
,
,,
四边形是平行四边形,
,
即的最小值为.
故答案为:.]
15.[提示:四边形是矩形,
,
平分,
,
是等腰直角三角形,
,
,
,故正确,
在和中,
,
,
,
,
,
,
,故正确;
,
,
,
,
,
,
,
,故正确;
连接.
,
,
,
,
,
,
,
,故正确.
故答案为:.]
16.、或[提示:如图,∵厘米,矩形从点开始以厘米/秒的速度沿直线向右运动,同时点从点出发沿的路线,以厘米/秒的速度运动,
∴开始运动秒后,点运动到点,
过点作于,则四边形和四边形以及四边形都是矩形,
∴(厘米),
设再过秒,则,
当点与点相距厘米时,即厘米,
∵厘米,,
∴,
解得或,
∴点共运动了秒或秒时,点与点相距厘米;
开始运动秒后,点运动到点,此时,厘米,如图,
设再过秒后,点与点相距厘米,
∵,
∴即,
解得(舍去)或,
∴点共运动了秒时,点与点相距厘米,
故答案为:、或.]
17.9.6/[提示:如图,取中点,连接,
四边形是菱形,
,,
是的中位线,
,,
又,
,
在的垂直平分线上,
,
,,
,
,
,
,
故答案为:9.6.]
18.[提示:∵四边形是矩形,
∴,,,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∵垂直平分线段,
∴,
∴四边形是菱形,
∵,
∴,
∴,
∴,
故答案为:.]
19./75度[提示:如图,设与相交于点E,
由翻折得,,
∵四边形是正方形,,
∴,
∴,
∴,
∴,
∴,
∴.]
20.或[提示:如图,当共线时,,
∵四边形是矩形,
∴,
∴,
由折叠性质可知:,,
∴,
设,则,
在中,由勾股定理得:,
即:,解得:,
如图,当落在上时,,
此时四边形为正方形,
∴,
综上可知:的长为或,
故答案为:或.]
21.(1)证明:∵,是的中位线,
∴,,
∴四边形是平行四边形
∵对角线、相交于点O,
∴;
(2)解:∵、是平行四边形的对角线,,
∴,
∵,是的中位线,
∴D,F分别是的中点
∴,
即.
22.(1)证明:∵四边形是平行四边形,
∴,即,
∵点分别是边的中点,
∴,即,
∴四边形是平行四边形;
(2)∵四边形是平行四边形,
∴,
∵,
∴四边形是平行四边形,
∴,
∵四边形是平行四边形,
∴,
又∵点是边的中点,
∴,
∴.
23.(1)证明:,,
四边形是平行四边形,
,
,
,
,
平行四边形是矩形;
(2)解:四边形是矩形,
,,
,
,
,
,
,
,
.
24.解;(1)由题意知,运动停止时,P点运动时间为秒,
∴,
∴,
∴运动停止时,的长为;
(2)如图,过D作于E,
∴四边形为矩形,
∴,,
∴,
∴,
由题可得,,若四边形为矩形,
则,即,
解得:,则,
∴;
(3)由题意知,分两种情况求解:
①当为平行四边形的边,则在点左侧,,,
∵,
∴,
解得;
②当为平行四边形的对角线,在点右侧,,,
∵,
∴,
解得 ,
综上所述,存在,当或时,以,,,为顶点的四边形为平行四边形.
25.(1)证明:∵,D是的中点,,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∴平行四边形是菱形.
(2)解:∵平行四边形是菱形,
∴,
∵D是的中点,
∴,
∴.
26.(1)证明:∵四边形是平行四边形,
,
∴,
∵E是的中点,
∴,
在△ADE和中,
,
∴,
∴.
(2)①等腰三角形,
连接AC,如图:
∵,
∴ ABCD是矩形,
∴,
∵,,
∴四边形是平行四边形.
∴.
∴.
∴△BDF是等腰三角形.
②55,
∵ ABCD是菱形,
∴,.
∴.
∵,
∴.
∴,
故答案为:等腰三角形;55.
27.(1)解:由翻折的性质可知,,
正方形纸片,
,
,
,
,
;
(2)解:延长到,使,
正方形纸片,
,
△ABT≌△ADQ(SAS),
,
,
,
,
,
△PAT≌△PAQ(SAS)
,
;
(3)解:,
,
,
,
,
在中,,
即,
解得或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
