第二章 二次函数 有关二次函数的最值问题 练习 北师大版数学九年级下册(含答案解析)
文档属性
| 名称 | 第二章 二次函数 有关二次函数的最值问题 练习 北师大版数学九年级下册(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 165.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 17:42:21 | ||
图片预览




文档简介
有关二次函数的最值问题
一.选择题(共10小题)
1.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
2.在二次函数y=x2﹣2x﹣3中,当0≤x≤3时,y的最大值和最小值分别是( )
A.0,﹣4 B.0,﹣3 C.﹣3,﹣4 D.0,0
3.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
4.当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A.﹣1 B.2 C.0或2 D.﹣1或2
5.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2 C.15cm2 D.12cm2
6.已知0≤x≤,那么函数y=﹣2x2+8x﹣6的最大值是( )
A.﹣10.5 B.2 C.﹣2.5 D.﹣6
7.如图,抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连接DC,DB,则△BCD的面积的最大值是( )
A.7 B.7.5 C.8 D.9
8.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或﹣ C.2或﹣ D.2或﹣或﹣
9.已知二次函数y=mx2+2mx+1(m≠0)在﹣2≤x≤2时有最小值﹣2,则m=( )
A.3 B.﹣3或 C.3或﹣ D.﹣3或﹣
10.已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4,则y1,y2,y3,y4的最值情况是( )
A.y3最小,y1最大 B.y3最小,y4最大 C.y1最小,y4最大 D.无法确定
二.填空题(共10小题)
11.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是 .
12.若函数y=x2﹣6x+5,当2≤x≤6时的最大值是M,最小值是m,则M﹣m= .
13.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 .
14.已知二次函数y=2(x+1)2+1,﹣2≤x≤1,则函数y的最小值是 ,最大值是 .
15.已知二次函数y=x2﹣2mx+1(m为常数),当自变量x的值满足﹣1≤x≤2时,与其对应的函数值y的最小值为﹣2,则m的值为 .
16.当﹣7≤x≤a时,二次函数y=﹣(x+3)2+5恰好有最大值3,则a= .
17.二次函数y=x2﹣2x+1在2≤x≤5范围内的最小值为 .
18.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是 .
19.二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,则a= .
20.设x≥0,y≥0,且2x+y=6,则μ=x2+2xy+y2﹣3x﹣2y的最小值是 .
三.解答题(共5小题)
21.设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{﹣1,﹣1}=﹣1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
(1)max{5,2}= ,max{0,3}= ;
(2)若max{3x+1,﹣x+1}=﹣x+1,求x的取值范围;
(3)求函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标,函数y=x2﹣2x﹣4的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,x2﹣2x﹣4}的最小值.
22.在平面直角坐标系xOy中,抛物线y=ax2+bx+a﹣4(a≠0)的对称轴是直线x=1.
(1)求抛物线y=ax2+bx+a﹣4(a≠0)的顶点坐标;
(2)当﹣2≤x≤3时,y的最大值是5,求a的值;
(3)在(2)的条件下,当t≤x≤t+1时,y的最大值是m,最小值是n,且m﹣n=3,求t的值.
23.如图,在Rt△ABC中,∠A=90°.AB=8cm,AC=6cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B,A重合的情况),运动速度为2cm/s,过点D作DE∥BC交AC于点E,连接BE,设动点D运动的时间为x(s),AE的长为y(cm).
(1)求y关于x的函数表达式,并写出自变量x的取值范围;
(2)当x为何值时,△BDE的面积S有最大值?最大值为多少?
24.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x … 0 1 2 3 4 …
y … 5 2 1 2 n …
(1)表中n的值为 ;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,且m>2,试比较y1与y2的大小.
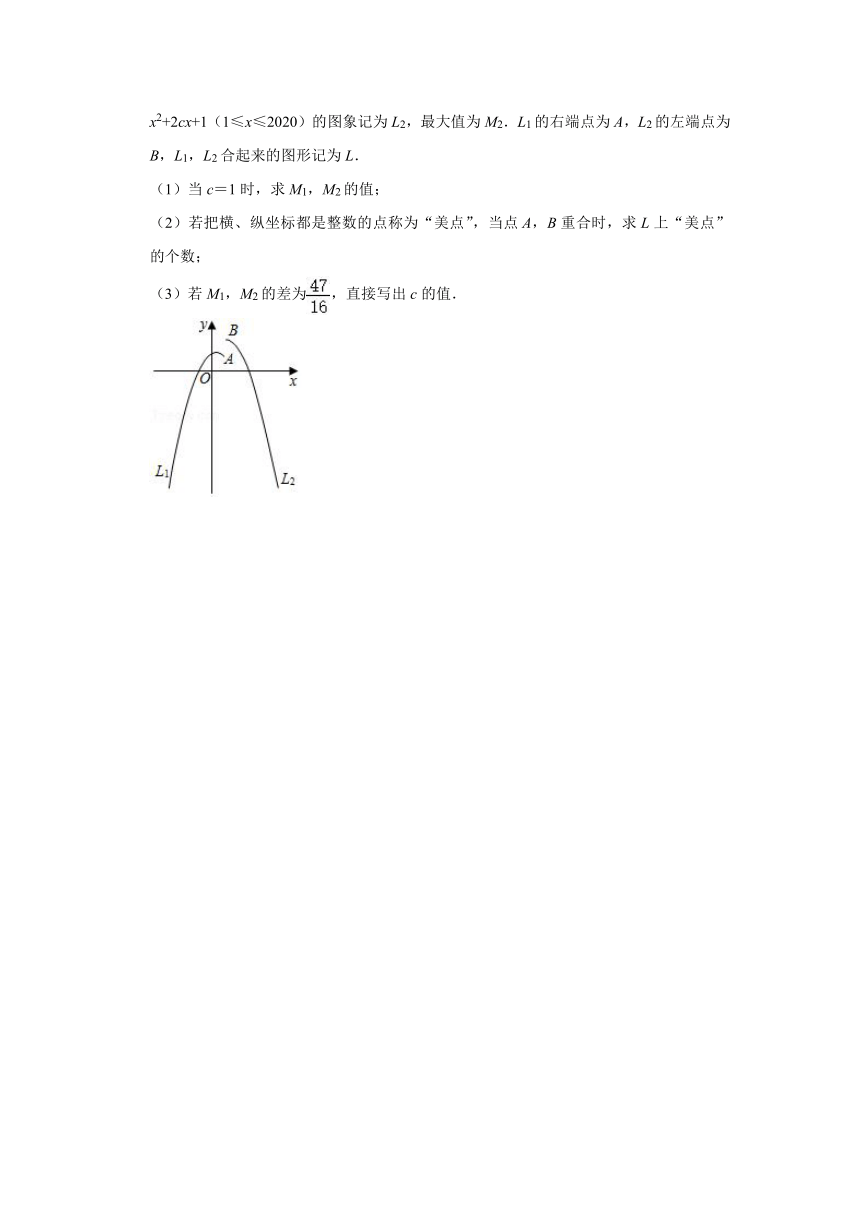
25.如图,函数y=﹣x2+x+c(﹣2020≤x≤1)的图象记为L1,最大值为M1;函数y=﹣x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
(1)当c=1时,求M1,M2的值;
(2)若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;
(3)若M1,M2的差为,直接写出c的值.
二次函数的最值精选题41道
参考答案与试题解析
一.选择题(共10小题)
1.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
解:二次函数的对称轴为直线x=m,
①m<﹣2时,x=﹣2时二次函数有最大值,此时﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,与m<﹣2矛盾,故m值不存在;
②当﹣2≤m≤1时,x=m时,二次函数有最大值,此时,m2+1=4,
解得m=﹣,m=(舍去);
③当m>1时,x=1时二次函数有最大值,此时,﹣(1﹣m)2+m2+1=4,解得m=2,
综上所述,m的值为2或﹣.故选:C.
2.在二次函数y=x2﹣2x﹣3中,当0≤x≤3时,y的最大值和最小值分别是( )
A.0,﹣4 B.0,﹣3 C.﹣3,﹣4 D.0,0
解:抛物线的对称轴是直线x=1,则当x=1时,y=1﹣2﹣3=﹣4,是最小值;
当x=3时,y=9﹣6﹣3=0是最大值.故选:A.
3.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
解:∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,
∴①若h<1≤x≤3,x=1时,y取得最小值5,可得:(1﹣h)2+1=5,
解得:h=﹣1或h=3(舍);
②若1≤x≤3<h,当x=3时,y取得最小值5,可得:(3﹣h)2+1=5,
解得:h=5或h=1(舍);
③若1≤h≤3时,当x=h时,y取得最小值为1,不是5,∴此种情况不符合题意,舍去.
综上,h的值为﹣1或5,故选:B.
4.当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A.﹣1 B.2 C.0或2 D.﹣1或2
解:当y=1时,有x2﹣2x+1=1,解得:x1=0,x2=2.
∵当a≤x≤a+1时,函数有最小值1,∴a=2或a+1=0,∴a=2或a=﹣1,
故选:D.
5.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2 C.15cm2 D.12cm2
解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,∴AC==6cm.
设运动时间为ts(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC﹣S△CPQ=AC BC﹣PC CQ=×6×8﹣(6﹣t)×2t=t2﹣6t+24=(t﹣3)2+15.
∵1>0,∴当t=3时,四边形PABQ的面积取最小值,最小值为15cm2.
6.已知0≤x≤,那么函数y=﹣2x2+8x﹣6的最大值是( )
A.﹣10.5 B.2 C.﹣2.5 D.﹣6
解:∵y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2.
∴该抛物线的对称轴是直线x=2,且在x<2上y随x的增大而增大.
又∵0≤x≤,∴当x=时,y取最大值,y最大=﹣2(﹣2)2+2=﹣2.5.
故选:C.
7.如图,抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连接DC,DB,则△BCD的面积的最大值是( )
A.7 B.7.5 C.8 D.9
解:设抛物线的解析式是y=ax2+bx+c,
∵抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,
∴解得,∴y=﹣x2+5x﹣4,
设过点B(4,0),C(0,﹣4)的直线的解析式为y=kx+m
解得,即直线BC的直线解析式为:y=x﹣4,
设点D的坐标是(x,﹣x2+5x﹣4)
∴=﹣2(x﹣2)2+8,
∴当x=2时,△BCD的面积取得最大值,最大值是8.故选:C.
8.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或﹣ C.2或﹣ D.2或﹣或﹣
解:二次函数对称轴为直线x=m,
①m<﹣2时,x=﹣2取得最大值,﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,不合题意,舍去;
②﹣2≤m≤1时,x=m取得最大值,m2+1=4,解得m=±,
∵m=不满足﹣2≤m≤1的范围,∴m=﹣;
③m>1时,x=1取得最大值,﹣(1﹣m)2+m2+1=4,解得m=2.
综上所述,m=2或﹣时,二次函数有最大值4.故选:C.
9.已知二次函数y=mx2+2mx+1(m≠0)在﹣2≤x≤2时有最小值﹣2,则m=( )
A.3 B.﹣3或 C.3或﹣ D.﹣3或﹣
解:∵二次函数y=mx2+2mx+1=m(x+1)2﹣m+1,∴对称轴为直线x=﹣1,
①m>0,抛物线开口向上,x=﹣1时,有最小值y=﹣m+1=﹣2,解得:m=3;
②m<0,抛物线开口向下,
∵对称轴为直线x=﹣1,在﹣2≤x≤2时有最小值﹣2,
∴x=2时,有最小值y=4m+4m+1=﹣2,解得:m=﹣;故选:C.
10.已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4,则y1,y2,y3,y4的最值情况是( )
A.y3最小,y1最大 B.y3最小,y4最大
C.y1最小,y4最大 D.无法确定
解:∵二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,且y3<y2<y4,∴抛物线开口向上,对称轴在0和1之间,
∴P1(﹣3,y1)离对称轴的距离最大,P3(1,y3)离对称轴距离最小,
∴y3最小,y1最大,故选:A.
二.填空题(共10小题)
11.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是 s≥9 .
解:由x+y2=3,得:y2=﹣x+3≥0,∴x≤3,
代入s=x2+8y2得:s=x2+8y2=x2+8(﹣x+3)=x2﹣8x+24=(x﹣4)2+8,
当x=3时,s=(3﹣4)2+8=9,∴s≥9;故答案为:s≥9.
12.若函数y=x2﹣6x+5,当2≤x≤6时的最大值是M,最小值是m,则M﹣m= 9 .
解:原式可化为y=(x﹣3)2﹣4,可知函数顶点坐标为(3,﹣4),
当y=0时,x2﹣6x+5=0,即(x﹣1)(x﹣5)=0,解得x1=1,x2=5.
如图:m=﹣4,当x=6时,y=36﹣36+5=5,即M=5.
则M﹣m=5﹣(﹣4)=9.故答案为9.
13.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 ﹣1.5或 .
解:由二次函数y=x2﹣2mx(m为常数),得到对称轴为直线x=m,抛物线开口向上,
当m>2时,由题意得:当x=2时,y最小值为﹣2,代入得:4﹣4m=﹣2,即m=1.5<2,不合题意,舍去;
当﹣1≤m≤2时,由题意得:当x=m时,y最小值为﹣2,代入得:﹣m2=﹣2,即m=或m=﹣(舍去);
当m<﹣1时,由题意得:当x=﹣1时,y最小值为﹣2,代入得:1+2m=﹣2,即m=﹣1.5,综上,m的值是﹣1.5或,故答案为:﹣1.5或.
14.已知二次函数y=2(x+1)2+1,﹣2≤x≤1,则函数y的最小值是 1 ,最大值是 9 .
解:由题意可得:y=2(x+1)2+1,﹣2≤x≤1
∵开口向上,∴当x=1时,有最大值:ymax=9,当x=﹣1时,ymin=1.故答案为1,9.
15.已知二次函数y=x2﹣2mx+1(m为常数),当自变量x的值满足﹣1≤x≤2时,与其对应的函数值y的最小值为﹣2,则m的值为 ﹣2或 .
解:由题意可知抛物线的对称轴为x=m,开口方向向上,
当m≤﹣1时,此时x=﹣1时,y可取得最小值﹣2,∴﹣2=1+2m+1,∴m=﹣2;
当﹣1<m<2时,∴此时x=m,y的最小值为﹣2,∴﹣2=m2﹣2m2+1,
∴m=±,∴m=;
当m≥2时,此时x=2时,y的最小值为﹣2,∴﹣2=4﹣4m+1,∴m=不符合题意,
故答案为:﹣2或.
16.当﹣7≤x≤a时,二次函数y=﹣(x+3)2+5恰好有最大值3,则a= ﹣5 .
解:∵y=﹣(x+3)2+5,∴该抛物线的开口方向向下,且顶点坐标是(﹣3,5).
∴当x<﹣3时,y随x的增大而增大,
∴当x=a时,二次函数y=﹣(x+3)2+5恰好有最大值3,
把y=3代入函数解析式得到 3=﹣(x+3)2+5,解得 x1=﹣5,x2=﹣1.
∴a=﹣5.故答案是:﹣5.
17.二次函数y=x2﹣2x+1在2≤x≤5范围内的最小值为 1 .
解:∵二次函数y=x2﹣2x+1=(x﹣1)2,∴当x>1时,y随x的增大而增大,
∴在2≤x≤5范围内,当x=2时,y取得最小值,此时y=(2﹣1)2=1,故答案为:1.
18.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是 ﹣4或2 .
解:∵y=﹣x2+mx,∴抛物线开口向下,抛物线的对称轴为x=﹣=,
∵=,
①当≤﹣1,即m≤﹣2时,当x=﹣1时,函数最大值为3,∴﹣1﹣m=3,
解得:m=﹣4;
②当≥2,即m≥4时,当x=2时,函数最大值为3,∴﹣4+2m=3,
解得:m=(舍去).
③当﹣1<<2,即﹣2<m<4时,当x=时,函数最大值为3,∴﹣+=3,
解得m=2或m=﹣2(舍去),综上所述,m=﹣4或m=2,
故答案为﹣4或2.
19.二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,则a= 1 .
解:y=x2﹣4x+a=(x﹣2)2+a﹣4,当x=2时,函数有最小值a﹣4,
∵二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,
∴a﹣4=﹣3,∴a=1,故答案为1.
20.设x≥0,y≥0,且2x+y=6,则μ=x2+2xy+y2﹣3x﹣2y的最小值是 0 .
解:由题意得:x≥0,y=6﹣2x≥0,解得:0≤x≤3.
∵μ=x2+2xy+y2﹣3x﹣2y=x2+2x(6﹣2x)+(6﹣2x)2﹣3x﹣2(6﹣2x)
=x2﹣11x+24=﹣,
∴当x≤ 时,y随x的增大而减小,故当x=3时,μ的最小值为﹣=0.
故答案为:0.
三.解答题(共5小题)
21.设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{﹣1,﹣1}=﹣1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
(1)max{5,2}= 5 ,max{0,3}= 3 ;
(2)若max{3x+1,﹣x+1}=﹣x+1,求x的取值范围;
(3)求函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标,函数y=x2﹣2x﹣4的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,x2﹣2x﹣4}的最小值.
解:(1)max{5,2}=5,max{0,3}=3.故答案为:5;3.
(2)∵max{3x+1,﹣x+1}=﹣x+1,∴3x+1≤﹣x+1,解得:x≤0.
(3)联立两函数解析式成方程组,
,解得:,,∴交点坐标为(﹣2,4)和(3,﹣1).
画出直线y=﹣x+2,如图所示,
观察函数图象可知:当x=3时,max{﹣x+2,x2﹣2x﹣4}取最小值﹣1.
22.在平面直角坐标系xOy中,抛物线y=ax2+bx+a﹣4(a≠0)的对称轴是直线x=1.
(1)求抛物线y=ax2+bx+a﹣4(a≠0)的顶点坐标;
(2)当﹣2≤x≤3时,y的最大值是5,求a的值;
(3)在(2)的条件下,当t≤x≤t+1时,y的最大值是m,最小值是n,且m﹣n=3,求t的值.
解:(1)将x=1代入抛物线y=ax2+bx+a﹣4得,y=a+b+a﹣4=2a+b﹣4,
∵对称轴是直线x=1.∴﹣=1,∴b=﹣2a,∴y=2a+b﹣4=2a﹣2a﹣4=﹣4,
∴抛物线y=ax2+bx+a﹣4(a≠0)的顶点坐标为(1,﹣4);
(2)①a<0时,抛物线开口向下,y的最大值是﹣4,
∵当﹣2≤x≤3时,y的最大值是5,∴a<0不合题意;
②a>0时,抛物线开口向上,
∵对称轴是直线x=1.1到﹣2的距离大于1到3的距离,∴x=﹣2时,y的值最大,
∴y=4a﹣2b+a﹣4=5a﹣2b﹣4=5,将b=﹣2a代入得,a=1;
(3)①t<0时,∵a=1,∴b=﹣2a=﹣2,
∴y的最大值是m=t2﹣2t+1﹣4=t2﹣2t﹣3,最小值是n=(t+1)2﹣2(t+1)﹣3,
∵m﹣n=3,∴t2﹣2t﹣3﹣[(t+1)2﹣2(t+1)﹣3]=3,解得:t=﹣1;
②≤t<1时,∴y的最大值是m=(t+1)2﹣2(t+1)﹣3,最小值是n=﹣4,
∵m﹣n=3,∴(t+1)2﹣2(t+1)﹣3﹣(﹣4)=3,解得:t=±(不成立);
③0<t≤时,y的最大值是m=t2﹣2t+1﹣4=t2﹣2t﹣3,最小值是n=﹣4,
m﹣n=t2﹣2t﹣3﹣(﹣4)=3,解得:t=±+1(不成立);
④t≥1时,∴y的最大值是m=(t+1)2﹣2(t+1)﹣3,最小值是n=t2﹣2t﹣3,
m﹣n=(t+1)2﹣2(t+1)﹣3﹣(t2﹣2t﹣3)=3,解得:t=2;
综上,t的值为﹣1或2.
23.如图,在Rt△ABC中,∠A=90°.AB=8cm,AC=6cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B,A重合的情况),运动速度为2cm/s,过点D作DE∥BC交AC于点E,连接BE,设动点D运动的时间为x(s),AE的长为y(cm).
(1)求y关于x的函数表达式,并写出自变量x的取值范围;
(2)当x为何值时,△BDE的面积S有最大值?最大值为多少?
解:(1)动点D运动x秒后,BD=2x.
又∵AB=8,∴AD=8﹣2x.∵DE∥BC,∴,∴,
∴y关于x的函数关系式为y=(0<x<4).
(2)解:S△BDE===(0<x<4).
当时,S△BDE最大,最大值为6cm2.
24.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x … 0 1 2 3 4 …
y … 5 2 1 2 n …
(1)表中n的值为 5 ;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,且m>2,试比较y1与y2的大小.
解:(1)∵根据表可知:对称轴是直线x=2,
∴点(0,5)和(4,n)关于直线x=2对称,∴n=5,故答案为:5;
(2)根据表可知:顶点坐标为(2,1),即当x=2时,y有最小值,最小值是1;
(3)∵函数的图象开口向上,顶点坐标为(2,1),对称轴是直线x=2,
∴当m>2时,点A(m1,y1),B(m+1,y2)都在对称轴的右侧,y随x的增大而增大,
∵m<m+1,∴y1<y2.
25.如图,函数y=﹣x2+x+c(﹣2020≤x≤1)的图象记为L1,最大值为M1;函数y=﹣x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
(1)当c=1时,求M1,M2的值;
(2)若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;
(3)若M1,M2的差为,直接写出c的值.
解:(1)当c=1时,函数y=﹣x2+x+c=﹣x2+x+1=﹣(x﹣)2+.
又∵﹣2020≤x≤1,∴M1=,y=﹣x2+2cx+1=﹣x2+2x+1=﹣(x﹣1)2+2.
又∵1≤x≤2020,∴M2=2;
(2)当x=1时,y=﹣x2+x+c=c﹣;y=﹣x2+2cx+1=2c.
若点A,B重合,则c﹣=2c,c=﹣,∴L1:y=﹣x2+x﹣(﹣2020≤x≤1);
L2:y=﹣x2﹣x+1(1≤x≤2020).
在L1上,x为奇数的点是“美点”,则L1上有1011个“美点”;
在L2上,x为整数的点是“美点”,则L2上有2020个“美点”.
又点A,B重合,则L上“美点”的个数是1011+2020﹣1=3030.
(3)y=﹣x2+x+c(﹣2020≤x≤1)上时,当x=时,M1=+c,
y=﹣x2+2cx+1(1≤x≤2020),对称轴为x=c,
当2020≥c≥1时,M2=c2+1,∴|+c﹣c2﹣1|=,∴c=﹣1(舍去)或c=2;
当c<1时,M2=2c,∴|2c﹣﹣c|=,∴c=3(舍去)或c=﹣;
∴c=﹣或2.
当c>2020时,M2=﹣20202+4040c+1,∴|﹣20202+4040c+1﹣﹣c|=,
∴c≈1010(舍弃),综上所述,c=﹣或2.
一.选择题(共10小题)
1.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
2.在二次函数y=x2﹣2x﹣3中,当0≤x≤3时,y的最大值和最小值分别是( )
A.0,﹣4 B.0,﹣3 C.﹣3,﹣4 D.0,0
3.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
4.当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A.﹣1 B.2 C.0或2 D.﹣1或2
5.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2 C.15cm2 D.12cm2
6.已知0≤x≤,那么函数y=﹣2x2+8x﹣6的最大值是( )
A.﹣10.5 B.2 C.﹣2.5 D.﹣6
7.如图,抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连接DC,DB,则△BCD的面积的最大值是( )
A.7 B.7.5 C.8 D.9
8.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或﹣ C.2或﹣ D.2或﹣或﹣
9.已知二次函数y=mx2+2mx+1(m≠0)在﹣2≤x≤2时有最小值﹣2,则m=( )
A.3 B.﹣3或 C.3或﹣ D.﹣3或﹣
10.已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4,则y1,y2,y3,y4的最值情况是( )
A.y3最小,y1最大 B.y3最小,y4最大 C.y1最小,y4最大 D.无法确定
二.填空题(共10小题)
11.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是 .
12.若函数y=x2﹣6x+5,当2≤x≤6时的最大值是M,最小值是m,则M﹣m= .
13.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 .
14.已知二次函数y=2(x+1)2+1,﹣2≤x≤1,则函数y的最小值是 ,最大值是 .
15.已知二次函数y=x2﹣2mx+1(m为常数),当自变量x的值满足﹣1≤x≤2时,与其对应的函数值y的最小值为﹣2,则m的值为 .
16.当﹣7≤x≤a时,二次函数y=﹣(x+3)2+5恰好有最大值3,则a= .
17.二次函数y=x2﹣2x+1在2≤x≤5范围内的最小值为 .
18.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是 .
19.二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,则a= .
20.设x≥0,y≥0,且2x+y=6,则μ=x2+2xy+y2﹣3x﹣2y的最小值是 .
三.解答题(共5小题)
21.设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{﹣1,﹣1}=﹣1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
(1)max{5,2}= ,max{0,3}= ;
(2)若max{3x+1,﹣x+1}=﹣x+1,求x的取值范围;
(3)求函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标,函数y=x2﹣2x﹣4的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,x2﹣2x﹣4}的最小值.
22.在平面直角坐标系xOy中,抛物线y=ax2+bx+a﹣4(a≠0)的对称轴是直线x=1.
(1)求抛物线y=ax2+bx+a﹣4(a≠0)的顶点坐标;
(2)当﹣2≤x≤3时,y的最大值是5,求a的值;
(3)在(2)的条件下,当t≤x≤t+1时,y的最大值是m,最小值是n,且m﹣n=3,求t的值.
23.如图,在Rt△ABC中,∠A=90°.AB=8cm,AC=6cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B,A重合的情况),运动速度为2cm/s,过点D作DE∥BC交AC于点E,连接BE,设动点D运动的时间为x(s),AE的长为y(cm).
(1)求y关于x的函数表达式,并写出自变量x的取值范围;
(2)当x为何值时,△BDE的面积S有最大值?最大值为多少?
24.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x … 0 1 2 3 4 …
y … 5 2 1 2 n …
(1)表中n的值为 ;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,且m>2,试比较y1与y2的大小.
25.如图,函数y=﹣x2+x+c(﹣2020≤x≤1)的图象记为L1,最大值为M1;函数y=﹣x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
(1)当c=1时,求M1,M2的值;
(2)若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;
(3)若M1,M2的差为,直接写出c的值.
二次函数的最值精选题41道
参考答案与试题解析
一.选择题(共10小题)
1.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
解:二次函数的对称轴为直线x=m,
①m<﹣2时,x=﹣2时二次函数有最大值,此时﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,与m<﹣2矛盾,故m值不存在;
②当﹣2≤m≤1时,x=m时,二次函数有最大值,此时,m2+1=4,
解得m=﹣,m=(舍去);
③当m>1时,x=1时二次函数有最大值,此时,﹣(1﹣m)2+m2+1=4,解得m=2,
综上所述,m的值为2或﹣.故选:C.
2.在二次函数y=x2﹣2x﹣3中,当0≤x≤3时,y的最大值和最小值分别是( )
A.0,﹣4 B.0,﹣3 C.﹣3,﹣4 D.0,0
解:抛物线的对称轴是直线x=1,则当x=1时,y=1﹣2﹣3=﹣4,是最小值;
当x=3时,y=9﹣6﹣3=0是最大值.故选:A.
3.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
解:∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,
∴①若h<1≤x≤3,x=1时,y取得最小值5,可得:(1﹣h)2+1=5,
解得:h=﹣1或h=3(舍);
②若1≤x≤3<h,当x=3时,y取得最小值5,可得:(3﹣h)2+1=5,
解得:h=5或h=1(舍);
③若1≤h≤3时,当x=h时,y取得最小值为1,不是5,∴此种情况不符合题意,舍去.
综上,h的值为﹣1或5,故选:B.
4.当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A.﹣1 B.2 C.0或2 D.﹣1或2
解:当y=1时,有x2﹣2x+1=1,解得:x1=0,x2=2.
∵当a≤x≤a+1时,函数有最小值1,∴a=2或a+1=0,∴a=2或a=﹣1,
故选:D.
5.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2 C.15cm2 D.12cm2
解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,∴AC==6cm.
设运动时间为ts(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC﹣S△CPQ=AC BC﹣PC CQ=×6×8﹣(6﹣t)×2t=t2﹣6t+24=(t﹣3)2+15.
∵1>0,∴当t=3时,四边形PABQ的面积取最小值,最小值为15cm2.
6.已知0≤x≤,那么函数y=﹣2x2+8x﹣6的最大值是( )
A.﹣10.5 B.2 C.﹣2.5 D.﹣6
解:∵y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2.
∴该抛物线的对称轴是直线x=2,且在x<2上y随x的增大而增大.
又∵0≤x≤,∴当x=时,y取最大值,y最大=﹣2(﹣2)2+2=﹣2.5.
故选:C.
7.如图,抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连接DC,DB,则△BCD的面积的最大值是( )
A.7 B.7.5 C.8 D.9
解:设抛物线的解析式是y=ax2+bx+c,
∵抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,
∴解得,∴y=﹣x2+5x﹣4,
设过点B(4,0),C(0,﹣4)的直线的解析式为y=kx+m
解得,即直线BC的直线解析式为:y=x﹣4,
设点D的坐标是(x,﹣x2+5x﹣4)
∴=﹣2(x﹣2)2+8,
∴当x=2时,△BCD的面积取得最大值,最大值是8.故选:C.
8.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或﹣ C.2或﹣ D.2或﹣或﹣
解:二次函数对称轴为直线x=m,
①m<﹣2时,x=﹣2取得最大值,﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,不合题意,舍去;
②﹣2≤m≤1时,x=m取得最大值,m2+1=4,解得m=±,
∵m=不满足﹣2≤m≤1的范围,∴m=﹣;
③m>1时,x=1取得最大值,﹣(1﹣m)2+m2+1=4,解得m=2.
综上所述,m=2或﹣时,二次函数有最大值4.故选:C.
9.已知二次函数y=mx2+2mx+1(m≠0)在﹣2≤x≤2时有最小值﹣2,则m=( )
A.3 B.﹣3或 C.3或﹣ D.﹣3或﹣
解:∵二次函数y=mx2+2mx+1=m(x+1)2﹣m+1,∴对称轴为直线x=﹣1,
①m>0,抛物线开口向上,x=﹣1时,有最小值y=﹣m+1=﹣2,解得:m=3;
②m<0,抛物线开口向下,
∵对称轴为直线x=﹣1,在﹣2≤x≤2时有最小值﹣2,
∴x=2时,有最小值y=4m+4m+1=﹣2,解得:m=﹣;故选:C.
10.已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4,则y1,y2,y3,y4的最值情况是( )
A.y3最小,y1最大 B.y3最小,y4最大
C.y1最小,y4最大 D.无法确定
解:∵二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,且y3<y2<y4,∴抛物线开口向上,对称轴在0和1之间,
∴P1(﹣3,y1)离对称轴的距离最大,P3(1,y3)离对称轴距离最小,
∴y3最小,y1最大,故选:A.
二.填空题(共10小题)
11.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是 s≥9 .
解:由x+y2=3,得:y2=﹣x+3≥0,∴x≤3,
代入s=x2+8y2得:s=x2+8y2=x2+8(﹣x+3)=x2﹣8x+24=(x﹣4)2+8,
当x=3时,s=(3﹣4)2+8=9,∴s≥9;故答案为:s≥9.
12.若函数y=x2﹣6x+5,当2≤x≤6时的最大值是M,最小值是m,则M﹣m= 9 .
解:原式可化为y=(x﹣3)2﹣4,可知函数顶点坐标为(3,﹣4),
当y=0时,x2﹣6x+5=0,即(x﹣1)(x﹣5)=0,解得x1=1,x2=5.
如图:m=﹣4,当x=6时,y=36﹣36+5=5,即M=5.
则M﹣m=5﹣(﹣4)=9.故答案为9.
13.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 ﹣1.5或 .
解:由二次函数y=x2﹣2mx(m为常数),得到对称轴为直线x=m,抛物线开口向上,
当m>2时,由题意得:当x=2时,y最小值为﹣2,代入得:4﹣4m=﹣2,即m=1.5<2,不合题意,舍去;
当﹣1≤m≤2时,由题意得:当x=m时,y最小值为﹣2,代入得:﹣m2=﹣2,即m=或m=﹣(舍去);
当m<﹣1时,由题意得:当x=﹣1时,y最小值为﹣2,代入得:1+2m=﹣2,即m=﹣1.5,综上,m的值是﹣1.5或,故答案为:﹣1.5或.
14.已知二次函数y=2(x+1)2+1,﹣2≤x≤1,则函数y的最小值是 1 ,最大值是 9 .
解:由题意可得:y=2(x+1)2+1,﹣2≤x≤1
∵开口向上,∴当x=1时,有最大值:ymax=9,当x=﹣1时,ymin=1.故答案为1,9.
15.已知二次函数y=x2﹣2mx+1(m为常数),当自变量x的值满足﹣1≤x≤2时,与其对应的函数值y的最小值为﹣2,则m的值为 ﹣2或 .
解:由题意可知抛物线的对称轴为x=m,开口方向向上,
当m≤﹣1时,此时x=﹣1时,y可取得最小值﹣2,∴﹣2=1+2m+1,∴m=﹣2;
当﹣1<m<2时,∴此时x=m,y的最小值为﹣2,∴﹣2=m2﹣2m2+1,
∴m=±,∴m=;
当m≥2时,此时x=2时,y的最小值为﹣2,∴﹣2=4﹣4m+1,∴m=不符合题意,
故答案为:﹣2或.
16.当﹣7≤x≤a时,二次函数y=﹣(x+3)2+5恰好有最大值3,则a= ﹣5 .
解:∵y=﹣(x+3)2+5,∴该抛物线的开口方向向下,且顶点坐标是(﹣3,5).
∴当x<﹣3时,y随x的增大而增大,
∴当x=a时,二次函数y=﹣(x+3)2+5恰好有最大值3,
把y=3代入函数解析式得到 3=﹣(x+3)2+5,解得 x1=﹣5,x2=﹣1.
∴a=﹣5.故答案是:﹣5.
17.二次函数y=x2﹣2x+1在2≤x≤5范围内的最小值为 1 .
解:∵二次函数y=x2﹣2x+1=(x﹣1)2,∴当x>1时,y随x的增大而增大,
∴在2≤x≤5范围内,当x=2时,y取得最小值,此时y=(2﹣1)2=1,故答案为:1.
18.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是 ﹣4或2 .
解:∵y=﹣x2+mx,∴抛物线开口向下,抛物线的对称轴为x=﹣=,
∵=,
①当≤﹣1,即m≤﹣2时,当x=﹣1时,函数最大值为3,∴﹣1﹣m=3,
解得:m=﹣4;
②当≥2,即m≥4时,当x=2时,函数最大值为3,∴﹣4+2m=3,
解得:m=(舍去).
③当﹣1<<2,即﹣2<m<4时,当x=时,函数最大值为3,∴﹣+=3,
解得m=2或m=﹣2(舍去),综上所述,m=﹣4或m=2,
故答案为﹣4或2.
19.二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,则a= 1 .
解:y=x2﹣4x+a=(x﹣2)2+a﹣4,当x=2时,函数有最小值a﹣4,
∵二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,
∴a﹣4=﹣3,∴a=1,故答案为1.
20.设x≥0,y≥0,且2x+y=6,则μ=x2+2xy+y2﹣3x﹣2y的最小值是 0 .
解:由题意得:x≥0,y=6﹣2x≥0,解得:0≤x≤3.
∵μ=x2+2xy+y2﹣3x﹣2y=x2+2x(6﹣2x)+(6﹣2x)2﹣3x﹣2(6﹣2x)
=x2﹣11x+24=﹣,
∴当x≤ 时,y随x的增大而减小,故当x=3时,μ的最小值为﹣=0.
故答案为:0.
三.解答题(共5小题)
21.设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{﹣1,﹣1}=﹣1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
(1)max{5,2}= 5 ,max{0,3}= 3 ;
(2)若max{3x+1,﹣x+1}=﹣x+1,求x的取值范围;
(3)求函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标,函数y=x2﹣2x﹣4的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,x2﹣2x﹣4}的最小值.
解:(1)max{5,2}=5,max{0,3}=3.故答案为:5;3.
(2)∵max{3x+1,﹣x+1}=﹣x+1,∴3x+1≤﹣x+1,解得:x≤0.
(3)联立两函数解析式成方程组,
,解得:,,∴交点坐标为(﹣2,4)和(3,﹣1).
画出直线y=﹣x+2,如图所示,
观察函数图象可知:当x=3时,max{﹣x+2,x2﹣2x﹣4}取最小值﹣1.
22.在平面直角坐标系xOy中,抛物线y=ax2+bx+a﹣4(a≠0)的对称轴是直线x=1.
(1)求抛物线y=ax2+bx+a﹣4(a≠0)的顶点坐标;
(2)当﹣2≤x≤3时,y的最大值是5,求a的值;
(3)在(2)的条件下,当t≤x≤t+1时,y的最大值是m,最小值是n,且m﹣n=3,求t的值.
解:(1)将x=1代入抛物线y=ax2+bx+a﹣4得,y=a+b+a﹣4=2a+b﹣4,
∵对称轴是直线x=1.∴﹣=1,∴b=﹣2a,∴y=2a+b﹣4=2a﹣2a﹣4=﹣4,
∴抛物线y=ax2+bx+a﹣4(a≠0)的顶点坐标为(1,﹣4);
(2)①a<0时,抛物线开口向下,y的最大值是﹣4,
∵当﹣2≤x≤3时,y的最大值是5,∴a<0不合题意;
②a>0时,抛物线开口向上,
∵对称轴是直线x=1.1到﹣2的距离大于1到3的距离,∴x=﹣2时,y的值最大,
∴y=4a﹣2b+a﹣4=5a﹣2b﹣4=5,将b=﹣2a代入得,a=1;
(3)①t<0时,∵a=1,∴b=﹣2a=﹣2,
∴y的最大值是m=t2﹣2t+1﹣4=t2﹣2t﹣3,最小值是n=(t+1)2﹣2(t+1)﹣3,
∵m﹣n=3,∴t2﹣2t﹣3﹣[(t+1)2﹣2(t+1)﹣3]=3,解得:t=﹣1;
②≤t<1时,∴y的最大值是m=(t+1)2﹣2(t+1)﹣3,最小值是n=﹣4,
∵m﹣n=3,∴(t+1)2﹣2(t+1)﹣3﹣(﹣4)=3,解得:t=±(不成立);
③0<t≤时,y的最大值是m=t2﹣2t+1﹣4=t2﹣2t﹣3,最小值是n=﹣4,
m﹣n=t2﹣2t﹣3﹣(﹣4)=3,解得:t=±+1(不成立);
④t≥1时,∴y的最大值是m=(t+1)2﹣2(t+1)﹣3,最小值是n=t2﹣2t﹣3,
m﹣n=(t+1)2﹣2(t+1)﹣3﹣(t2﹣2t﹣3)=3,解得:t=2;
综上,t的值为﹣1或2.
23.如图,在Rt△ABC中,∠A=90°.AB=8cm,AC=6cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B,A重合的情况),运动速度为2cm/s,过点D作DE∥BC交AC于点E,连接BE,设动点D运动的时间为x(s),AE的长为y(cm).
(1)求y关于x的函数表达式,并写出自变量x的取值范围;
(2)当x为何值时,△BDE的面积S有最大值?最大值为多少?
解:(1)动点D运动x秒后,BD=2x.
又∵AB=8,∴AD=8﹣2x.∵DE∥BC,∴,∴,
∴y关于x的函数关系式为y=(0<x<4).
(2)解:S△BDE===(0<x<4).
当时,S△BDE最大,最大值为6cm2.
24.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x … 0 1 2 3 4 …
y … 5 2 1 2 n …
(1)表中n的值为 5 ;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,且m>2,试比较y1与y2的大小.
解:(1)∵根据表可知:对称轴是直线x=2,
∴点(0,5)和(4,n)关于直线x=2对称,∴n=5,故答案为:5;
(2)根据表可知:顶点坐标为(2,1),即当x=2时,y有最小值,最小值是1;
(3)∵函数的图象开口向上,顶点坐标为(2,1),对称轴是直线x=2,
∴当m>2时,点A(m1,y1),B(m+1,y2)都在对称轴的右侧,y随x的增大而增大,
∵m<m+1,∴y1<y2.
25.如图,函数y=﹣x2+x+c(﹣2020≤x≤1)的图象记为L1,最大值为M1;函数y=﹣x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
(1)当c=1时,求M1,M2的值;
(2)若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;
(3)若M1,M2的差为,直接写出c的值.
解:(1)当c=1时,函数y=﹣x2+x+c=﹣x2+x+1=﹣(x﹣)2+.
又∵﹣2020≤x≤1,∴M1=,y=﹣x2+2cx+1=﹣x2+2x+1=﹣(x﹣1)2+2.
又∵1≤x≤2020,∴M2=2;
(2)当x=1时,y=﹣x2+x+c=c﹣;y=﹣x2+2cx+1=2c.
若点A,B重合,则c﹣=2c,c=﹣,∴L1:y=﹣x2+x﹣(﹣2020≤x≤1);
L2:y=﹣x2﹣x+1(1≤x≤2020).
在L1上,x为奇数的点是“美点”,则L1上有1011个“美点”;
在L2上,x为整数的点是“美点”,则L2上有2020个“美点”.
又点A,B重合,则L上“美点”的个数是1011+2020﹣1=3030.
(3)y=﹣x2+x+c(﹣2020≤x≤1)上时,当x=时,M1=+c,
y=﹣x2+2cx+1(1≤x≤2020),对称轴为x=c,
当2020≥c≥1时,M2=c2+1,∴|+c﹣c2﹣1|=,∴c=﹣1(舍去)或c=2;
当c<1时,M2=2c,∴|2c﹣﹣c|=,∴c=3(舍去)或c=﹣;
∴c=﹣或2.
当c>2020时,M2=﹣20202+4040c+1,∴|﹣20202+4040c+1﹣﹣c|=,
∴c≈1010(舍弃),综上所述,c=﹣或2.
