数学人教A版(2019)选择性必修第二册5.3.1函数的单调性 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册5.3.1函数的单调性 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 19:03:19 | ||
图片预览





文档简介
(共15张PPT)
复习巩固
①导数的加、减法运算法则:
②导数的乘法运算法则:
③导数的除法运算法则:
导数的四则运算法则
I
一般地,对于由函数和复合而成的函数,它的导数与函数,的导数间的关系为
复合函数的求导法则
II
第五章 一元函数的导数及其应用
5.3.1 函数的单调性
延时符
学习目标
结合实例,借助几何直观了解函数的单调性与导数的关系
能利用导数研究函数的单调性
数学抽象、数学运算、直观想象
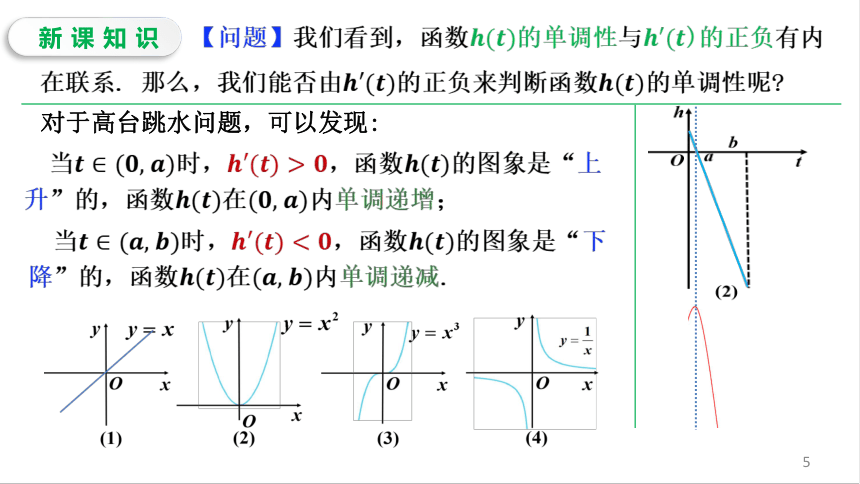
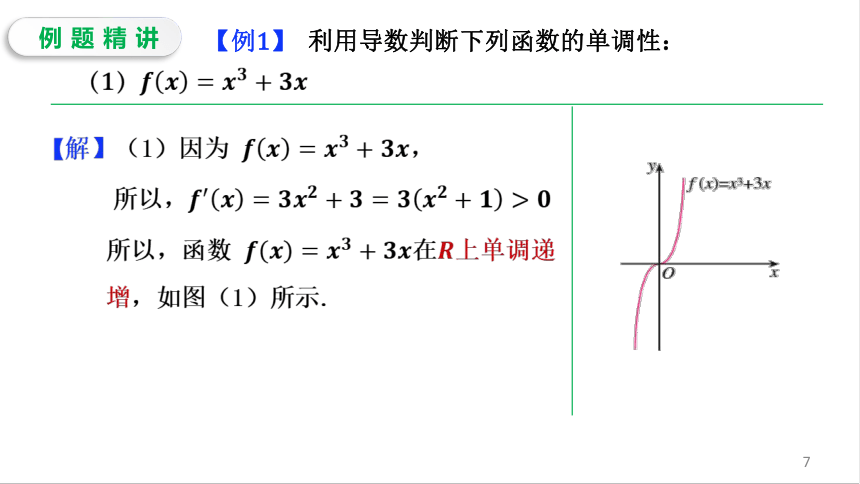
新知导入(阅读教材84页思考)的的图象.,是函数的零点. (2)从最高点到入水,运动员的重心处于下降状态,离水面的高度随时间t的增加而减小,即单调递减.相应地,.观察图象可以发现:(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度随时间的增加而增加,即单调递增.相应地,新课知识【问题】我们看到,函数的单调性与)的正负有内在联系.那么,我们能否由的正负来判断函数的单调性呢 当时,,函数的图象是“下降”的,函数在内单调递减.对于高台跳水问题,可以发现:当时,,函数的图象是“上升”的,函数在内单调递增;新课知识在某个区间上,如果,那么函数在区间上单调递减.函数的单调性与导数的关系一般地,函数的单调性与导函数的正负之间具有如下的关系: 在某个区间上,如果,那么函数在区间上单调递增; 例题精讲【例1】利用导数判断下列函数的单调性:(1)【解】(1)因为,所以,所以,函数在上单调递增,如图(1)所示.例题精讲所以,函数上单调递减,如图(2)所示.(2)【例1】利用导数判断下列函数的单调性:【解】因为,所以,例题精讲【解】因为(3)【例1】利用导数判断下列函数的单调性:所以,函数上单调递增,如图(3)所示.例题精讲【例2】已知导函数的下列信息:当时,;当,或时,;当,或时,.试画出函数图象的大致形状.当或时,,这两点比较特殊,我们称它们为“稳定点”.综上,函数图象的大致形状如图所示.0 0单调递减单调递增单调递减课堂练习课堂练习课堂小结判定函数单调性的步骤在某个区间上,如果,那么函数在区间上单调递减.一般地,函数的单调性与导函数的正负之间具有如下的关系:在某个区间上,如果,那么函数在区间上单调递增;求出函数的定义域;1求出函数的导数; 2判定导数的符号; 3确定函数的单调性. 4
本课作业
必做 二
必做 一
必做 三
教材 97 页
习题 1~2
三维 248页
课后 11,12
三维 248页
课后 11,12
01
02
03
微信: 手机:
感谢您的观看
复习巩固
①导数的加、减法运算法则:
②导数的乘法运算法则:
③导数的除法运算法则:
导数的四则运算法则
I
一般地,对于由函数和复合而成的函数,它的导数与函数,的导数间的关系为
复合函数的求导法则
II
第五章 一元函数的导数及其应用
5.3.1 函数的单调性
延时符
学习目标
结合实例,借助几何直观了解函数的单调性与导数的关系
能利用导数研究函数的单调性
数学抽象、数学运算、直观想象
新知导入(阅读教材84页思考)的的图象.,是函数的零点. (2)从最高点到入水,运动员的重心处于下降状态,离水面的高度随时间t的增加而减小,即单调递减.相应地,.观察图象可以发现:(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度随时间的增加而增加,即单调递增.相应地,新课知识【问题】我们看到,函数的单调性与)的正负有内在联系.那么,我们能否由的正负来判断函数的单调性呢 当时,,函数的图象是“下降”的,函数在内单调递减.对于高台跳水问题,可以发现:当时,,函数的图象是“上升”的,函数在内单调递增;新课知识在某个区间上,如果,那么函数在区间上单调递减.函数的单调性与导数的关系一般地,函数的单调性与导函数的正负之间具有如下的关系: 在某个区间上,如果,那么函数在区间上单调递增; 例题精讲【例1】利用导数判断下列函数的单调性:(1)【解】(1)因为,所以,所以,函数在上单调递增,如图(1)所示.例题精讲所以,函数上单调递减,如图(2)所示.(2)【例1】利用导数判断下列函数的单调性:【解】因为,所以,例题精讲【解】因为(3)【例1】利用导数判断下列函数的单调性:所以,函数上单调递增,如图(3)所示.例题精讲【例2】已知导函数的下列信息:当时,;当,或时,;当,或时,.试画出函数图象的大致形状.当或时,,这两点比较特殊,我们称它们为“稳定点”.综上,函数图象的大致形状如图所示.0 0单调递减单调递增单调递减课堂练习课堂练习课堂小结判定函数单调性的步骤在某个区间上,如果,那么函数在区间上单调递减.一般地,函数的单调性与导函数的正负之间具有如下的关系:在某个区间上,如果,那么函数在区间上单调递增;求出函数的定义域;1求出函数的导数; 2判定导数的符号; 3确定函数的单调性. 4
本课作业
必做 二
必做 一
必做 三
教材 97 页
习题 1~2
三维 248页
课后 11,12
三维 248页
课后 11,12
01
02
03
微信: 手机:
感谢您的观看
