1.6.1 完全平方公式(第1课时) 课件(共24张PPT)
文档属性
| 名称 | 1.6.1 完全平方公式(第1课时) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 720.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
新课标 北师大版
七年级下册
1.6.1完全平方公式(第1课时)
第一章
整式的乘除
学习目标
1.理解并掌握完全平方公式.
2.会运用公式进行简单的计算.
3.体会数学整体思想,发展几何直观.
新课引入
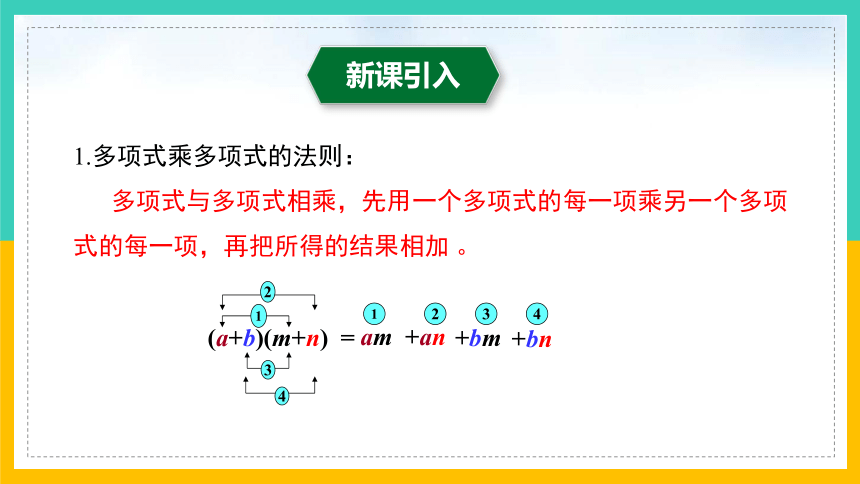
1.多项式乘多项式的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的结果相加 。
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
新课引入
七年级2班的49名同学准备定制统一的T恤去春游,据了解,一件T恤的价格为49元,班长小亮正在计算总的费用时,小明立马给出答案,2401元。你知道小明为什么算这么快吗?
49×49=?
核心知识点一
探究学习
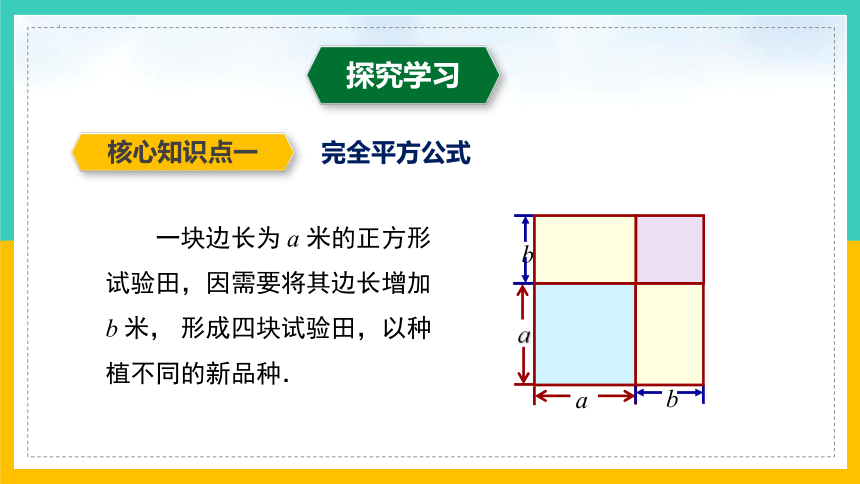
完全平方公式
a
a
b
b
一块边长为 a 米的正方形试验田,因需要将其边长增加 b 米, 形成四块试验田,以种植不同的新品种.
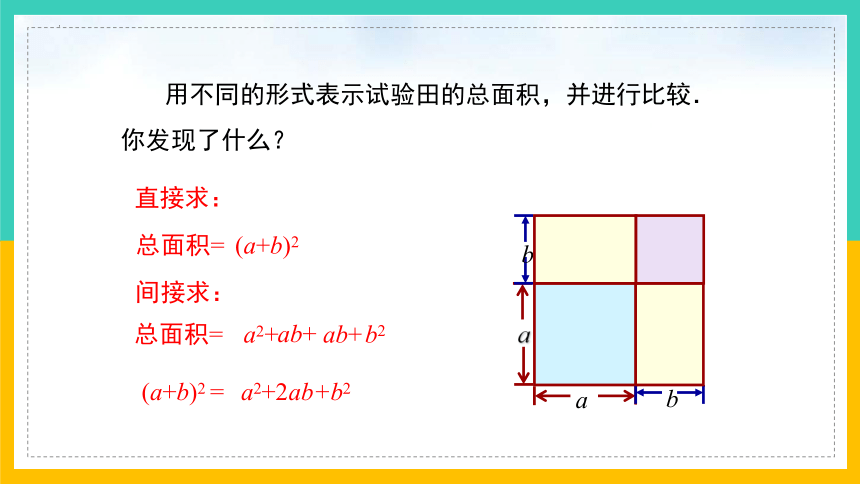
直接求:
总面积=
(a+b)2
间接求:
总面积=
a2+
ab+
ab+
b2
(a+b)2 =
a2+2ab+b2
用不同的形式表示试验田的总面积,并进行比较.
你发现了什么?
a
a
b
b
2
从运算的角度验证:
(a+b)2 = a2+2ab+b2
(a+b)2 = (a+b)(a+b) ---------- 幂的意义
= a(a+b)+b(a+b)
= a2+ab+ab+b2
= a2+2ab+b2 ----------多项式乘法法则
所以 :(a+b)2 = a2+2·a·b+b2
平方
平方
想一想: (a-b)2 等于什么呢?
(a-b)2 = (a-b)(a-b) ---------- 幂的意义
= a(a-b)-b(a-b)
= a2-ab-ab+b2
= a2-2ab+b2 ----------多项式乘法法则
所以 :(a-b)2 = a2+2·a·b+b2
平方
平方
同理:
两数和的平方,等于它们平方的和,加上它们乘积的两倍;
(a+b) =a +2ab+b
两数差的平方,等于它们平方的和,减去它们乘积的两倍.
(a-b) =a -2ab+ b
这两个公式统称为完全平方公式
即:两数和(或差)的平方,等于它们的平方和,加上(或者减去)它们的积的2倍.
完全平方公式
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
简记为:
“首平方,尾平方,
积的2倍放中间”
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
1.形式不同.
注意完全平方公式和平方差公式的不同:
2.结果不同
完全平方公式的结果是三项,
即:(a±b)2=a2±2ab+b2
平方差公式的结果是两项,
即:(a+b) (a-b) =a2-b2
注意完全平方公式和平方差公式的“共同”:
1.要找准对应公式中的a和b
2.掌握常见的变形和必要时添加括号
完全平方公式的图形理解
a
a
b
b
(a+b)2 = a2+2ab+b2
a
b
ab
ab
a
a
b
b
(a-b)
b
b(a-b)
b(a-b)
(a-b)2 = a2-2b(a-b)-b2
=a2-2ab+b2
例1:运用完全平方公式计算:
(1)(2x-3)2;(2)(4x+5y)2;(3)(mn-a)2 .
解:(1) (2x-3)2=
=4x2
(2x)2
-2 (2x) 3
+32
-12x
+9;
( a- b )2 = a2 - 2ab + b2
(2)(4x+5y)2 = (4x)2 +2·4x·5y+ (5y)2
= 16x2 +40xy+ 25y2 ;
( a + b )2 = a2 + 2ab + b2
(3) (mn-a)2 = (mn)2-2·mn·a+a2
= m2n2-2amn+a2.
( a - b )2 = a2 - 2ab + b2
例2:利用完全平方公式计算:
(1) (-1-2x)2 (2) (-2x+1)2
解:(1) (-1-2x)2
=(-1)2-2·(-1)·2x+(2x)2=1+4x+4x2
=[(-1)+(-2x)]2=(-1)2+2·(-1)·(-2x)+(-2x)2=1+4x+4x2
=[-(1+2x)]2=(1+2x)2=1+4x+4x2
还有其他方法吗?
方法2:
(-1-2x)2
方法3:
(-1-2x)2
(2) (-2x+1)2
=(-2x)2 +2·(-2x)·1+12=4x2-4x+1
方法2:
(-2x+1)2
=(2x-1)2
=4x2-4x+1
随堂练习
1.下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3)(x+2y)2 =x2 +2xy +4y2
×
×
×
x2+2xy +y2
x2-2xy +y2
x2+4xy +4y2
(4) (3x-y)2 =3x2 -6xy +y2
×
9x2-6xy +y2
2. 已知x+y=-5,xy=3,则x2+y2=( )
A. 25 B. -25
C. 19 D. -19
3. 在下列运算中,计算正确的是( )
A. (x5)2=x7 B. (x-y)2=x2-y2
C. x13÷x3=x10 D. x3+x3=x6
C
C
4. 计算 ,正确的结果是( )
A. 4x2+ y2 B. 4x2-2xy+ y2
C. 4x2-xy+ y2 D. 4x2- y2
5.已知m+n=3,则m2+2mn+n2-6的值为( )
A. 12 B. 6
C. 3 D.0
B
C
6. 若代数式x2+kx+25是一个完全平方式,则k=_________.
7. 若a+b=5,ab=6,则(a-b)2=____________.
±10
1
8. 若(x-3y)2=x2-6xy+(ky)2,则k=____________.
±3
9. 计算:
(1)(n+4)2-n2;
(2)(-2a+1)2.
解:原式=n2+8n+16-n2
=8n+16
解:原式=(-2a)2+2·(-2a)+12
=4a2-4a+1
10.计算
(1)(3a+b-2)(3a-b+2);
(2)(x-y-m+n)(x-y+m-n).
(2)原式=[(x-y)-(m-n)][(x-y)+(m-n)]
解:(1)原式=[3a+(b-2)][3a-(b-2)]
=(3a)2-(b-2)2
=9a2-b2+4b-4.
=(x-y)2-(m-n)2
=x2-2xy+y2-m2+2mn-n2.
解:∵36x2+(m+1)xy+25y2
=(±6x)2+(m+1)xy+(±5y)2,
∴(m+1)xy=±2·6x·5y,
∴m+1=±60,
∴m=59或-61.
11.如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.
课堂小结
谢谢聆听
新课标 北师大版
七年级下册
1.6.1完全平方公式(第1课时)
第一章
整式的乘除
学习目标
1.理解并掌握完全平方公式.
2.会运用公式进行简单的计算.
3.体会数学整体思想,发展几何直观.
新课引入
1.多项式乘多项式的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的结果相加 。
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
新课引入
七年级2班的49名同学准备定制统一的T恤去春游,据了解,一件T恤的价格为49元,班长小亮正在计算总的费用时,小明立马给出答案,2401元。你知道小明为什么算这么快吗?
49×49=?
核心知识点一
探究学习
完全平方公式
a
a
b
b
一块边长为 a 米的正方形试验田,因需要将其边长增加 b 米, 形成四块试验田,以种植不同的新品种.
直接求:
总面积=
(a+b)2
间接求:
总面积=
a2+
ab+
ab+
b2
(a+b)2 =
a2+2ab+b2
用不同的形式表示试验田的总面积,并进行比较.
你发现了什么?
a
a
b
b
2
从运算的角度验证:
(a+b)2 = a2+2ab+b2
(a+b)2 = (a+b)(a+b) ---------- 幂的意义
= a(a+b)+b(a+b)
= a2+ab+ab+b2
= a2+2ab+b2 ----------多项式乘法法则
所以 :(a+b)2 = a2+2·a·b+b2
平方
平方
想一想: (a-b)2 等于什么呢?
(a-b)2 = (a-b)(a-b) ---------- 幂的意义
= a(a-b)-b(a-b)
= a2-ab-ab+b2
= a2-2ab+b2 ----------多项式乘法法则
所以 :(a-b)2 = a2+2·a·b+b2
平方
平方
同理:
两数和的平方,等于它们平方的和,加上它们乘积的两倍;
(a+b) =a +2ab+b
两数差的平方,等于它们平方的和,减去它们乘积的两倍.
(a-b) =a -2ab+ b
这两个公式统称为完全平方公式
即:两数和(或差)的平方,等于它们的平方和,加上(或者减去)它们的积的2倍.
完全平方公式
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
简记为:
“首平方,尾平方,
积的2倍放中间”
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
1.形式不同.
注意完全平方公式和平方差公式的不同:
2.结果不同
完全平方公式的结果是三项,
即:(a±b)2=a2±2ab+b2
平方差公式的结果是两项,
即:(a+b) (a-b) =a2-b2
注意完全平方公式和平方差公式的“共同”:
1.要找准对应公式中的a和b
2.掌握常见的变形和必要时添加括号
完全平方公式的图形理解
a
a
b
b
(a+b)2 = a2+2ab+b2
a
b
ab
ab
a
a
b
b
(a-b)
b
b(a-b)
b(a-b)
(a-b)2 = a2-2b(a-b)-b2
=a2-2ab+b2
例1:运用完全平方公式计算:
(1)(2x-3)2;(2)(4x+5y)2;(3)(mn-a)2 .
解:(1) (2x-3)2=
=4x2
(2x)2
-2 (2x) 3
+32
-12x
+9;
( a- b )2 = a2 - 2ab + b2
(2)(4x+5y)2 = (4x)2 +2·4x·5y+ (5y)2
= 16x2 +40xy+ 25y2 ;
( a + b )2 = a2 + 2ab + b2
(3) (mn-a)2 = (mn)2-2·mn·a+a2
= m2n2-2amn+a2.
( a - b )2 = a2 - 2ab + b2
例2:利用完全平方公式计算:
(1) (-1-2x)2 (2) (-2x+1)2
解:(1) (-1-2x)2
=(-1)2-2·(-1)·2x+(2x)2=1+4x+4x2
=[(-1)+(-2x)]2=(-1)2+2·(-1)·(-2x)+(-2x)2=1+4x+4x2
=[-(1+2x)]2=(1+2x)2=1+4x+4x2
还有其他方法吗?
方法2:
(-1-2x)2
方法3:
(-1-2x)2
(2) (-2x+1)2
=(-2x)2 +2·(-2x)·1+12=4x2-4x+1
方法2:
(-2x+1)2
=(2x-1)2
=4x2-4x+1
随堂练习
1.下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3)(x+2y)2 =x2 +2xy +4y2
×
×
×
x2+2xy +y2
x2-2xy +y2
x2+4xy +4y2
(4) (3x-y)2 =3x2 -6xy +y2
×
9x2-6xy +y2
2. 已知x+y=-5,xy=3,则x2+y2=( )
A. 25 B. -25
C. 19 D. -19
3. 在下列运算中,计算正确的是( )
A. (x5)2=x7 B. (x-y)2=x2-y2
C. x13÷x3=x10 D. x3+x3=x6
C
C
4. 计算 ,正确的结果是( )
A. 4x2+ y2 B. 4x2-2xy+ y2
C. 4x2-xy+ y2 D. 4x2- y2
5.已知m+n=3,则m2+2mn+n2-6的值为( )
A. 12 B. 6
C. 3 D.0
B
C
6. 若代数式x2+kx+25是一个完全平方式,则k=_________.
7. 若a+b=5,ab=6,则(a-b)2=____________.
±10
1
8. 若(x-3y)2=x2-6xy+(ky)2,则k=____________.
±3
9. 计算:
(1)(n+4)2-n2;
(2)(-2a+1)2.
解:原式=n2+8n+16-n2
=8n+16
解:原式=(-2a)2+2·(-2a)+12
=4a2-4a+1
10.计算
(1)(3a+b-2)(3a-b+2);
(2)(x-y-m+n)(x-y+m-n).
(2)原式=[(x-y)-(m-n)][(x-y)+(m-n)]
解:(1)原式=[3a+(b-2)][3a-(b-2)]
=(3a)2-(b-2)2
=9a2-b2+4b-4.
=(x-y)2-(m-n)2
=x2-2xy+y2-m2+2mn-n2.
解:∵36x2+(m+1)xy+25y2
=(±6x)2+(m+1)xy+(±5y)2,
∴(m+1)xy=±2·6x·5y,
∴m+1=±60,
∴m=59或-61.
11.如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
