10.2.1 直方图(第一课时) 课件(共37张PPT)
文档属性
| 名称 | 10.2.1 直方图(第一课时) 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览



文档简介
(共37张PPT)
第10章 数据的收集、整理与描述
10.2.1 直方图(第一课时)
第六单元
1.理解频数、频率的定义; (重点)
2.频数和频率的相关计算; (难点)
3.会画简单的频数分布直方图等距分组.(难点)
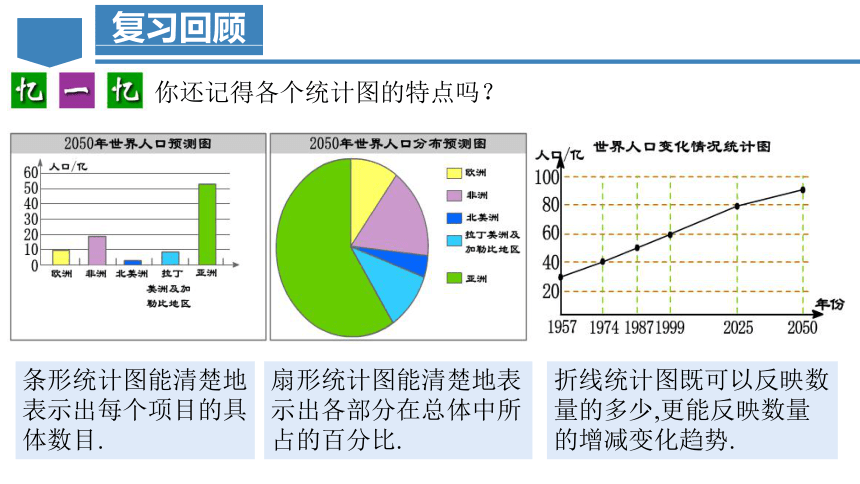
你还记得各个统计图的特点吗?
折线统计图既可以反映数量的多少,更能反映数量的增减变化趋势.
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
条形统计图能清楚地表示出每个项目的具体数目.
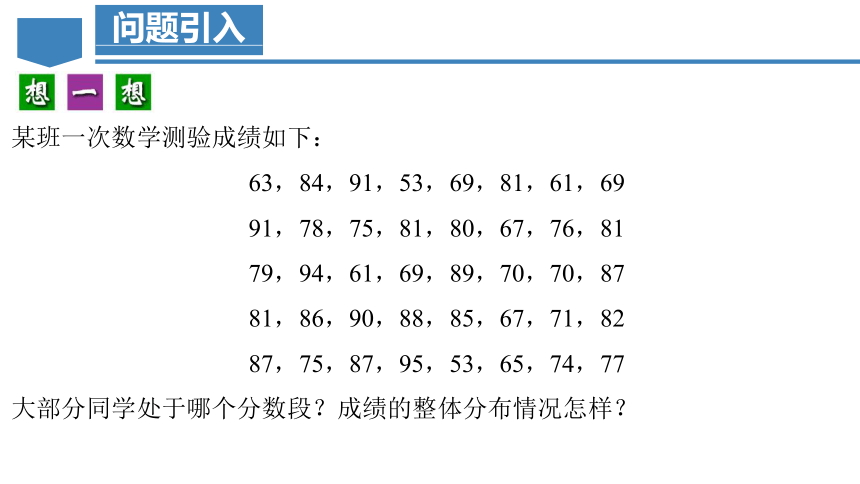
某班一次数学测验成绩如下:
63,84,91,53,69,81,61,69
91,78,75,81,80,67,76,81
79,94,61,69,89,70,70,87
81,86,90,88,85,67,71,82
87,75,87,95,53,65,74,77
大部分同学处于哪个分数段?成绩的整体分布情况怎样?
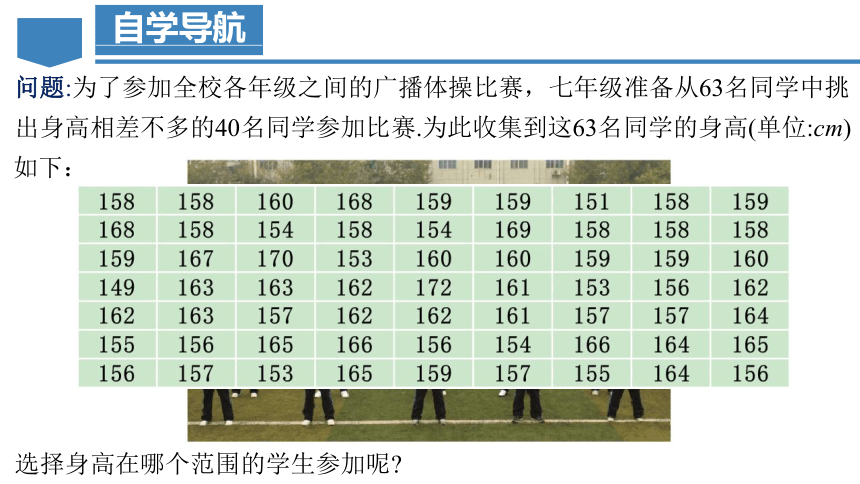
问题:为了参加全校各年级之间的广播体操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.
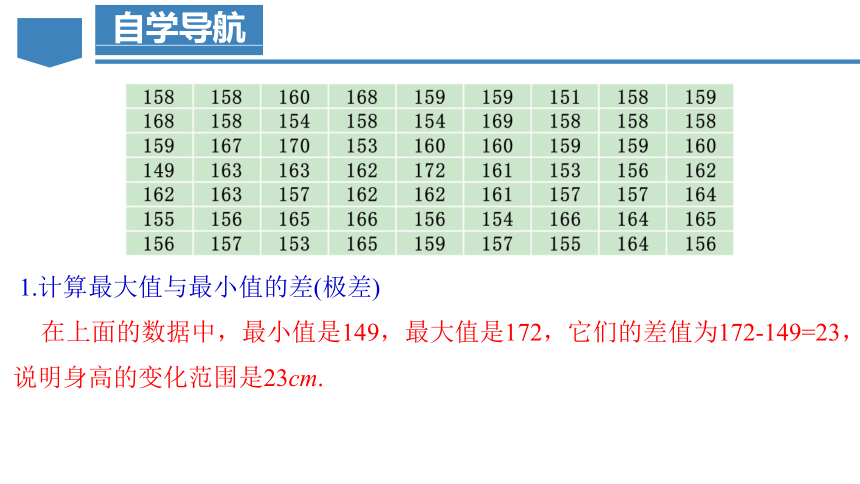
为此收集到这63名同学的身高(单位:cm)如下:
选择身高在哪个范围的学生参加呢
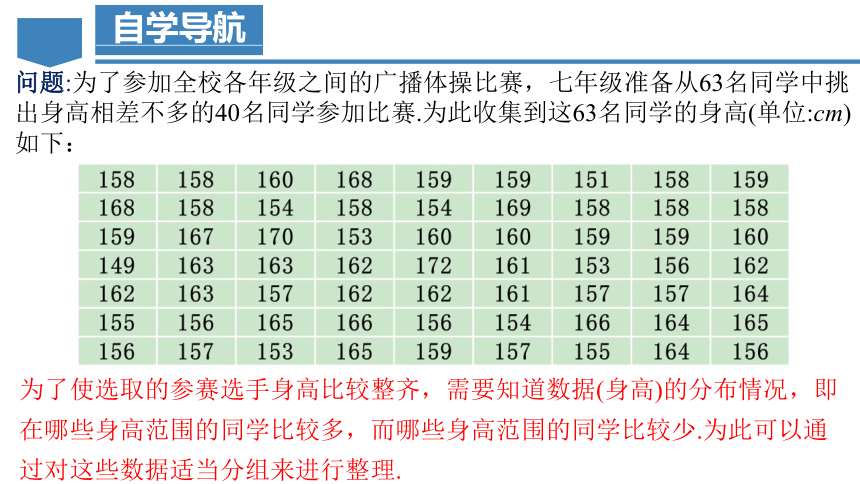
问题:为了参加全校各年级之间的广播体操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况,即在哪些身高范围的同学比较多,而哪些身高范围的同学比较少.为此可以通过对这些数据适当分组来进行整理.
1.计算最大值与最小值的差(极差)
在上面的数据中,最小值是149,最大值是172,它们的差值为172-149=23,说明身高的变化范围是23cm.
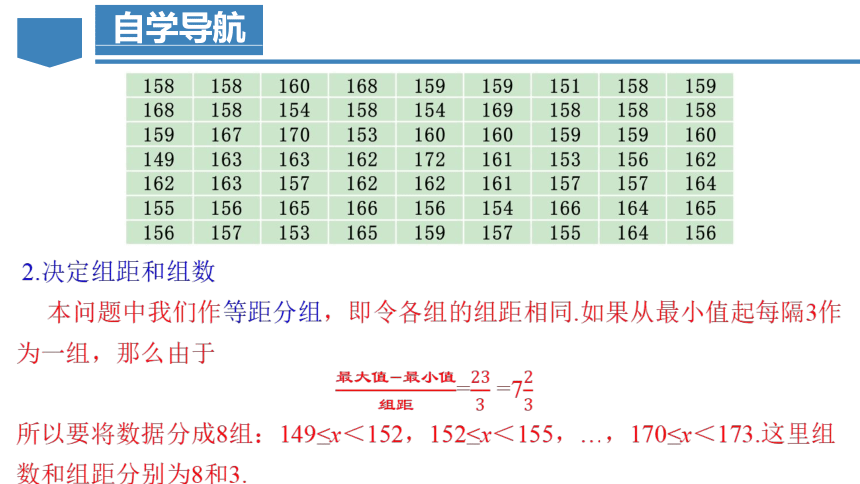
2.决定组距和组数
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3作为一组,那么由于
= =7
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别为8和3.
2.决定组距和组数
组距和组数的确定没有固定标准,要凭借经验和所研究的具体问题来决定.将一批数据分组,一般数据越多分的组数也越多.当数据在100个以内时,按照数据的多少,常分成5~12组.
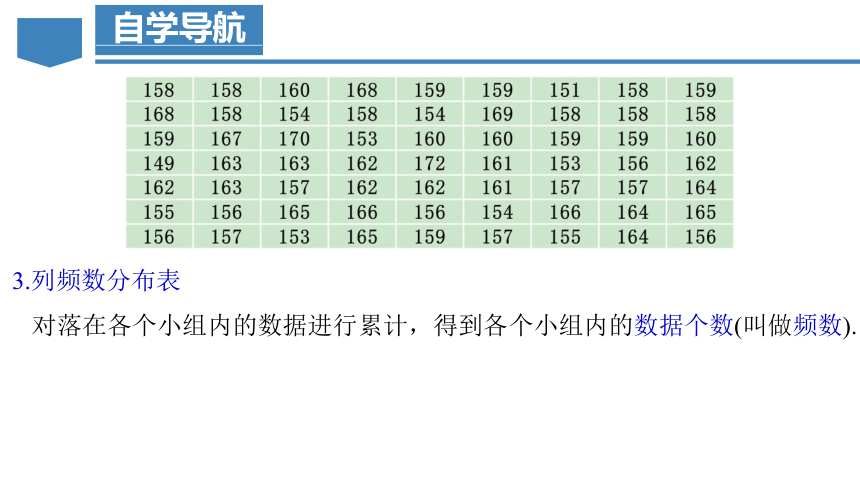
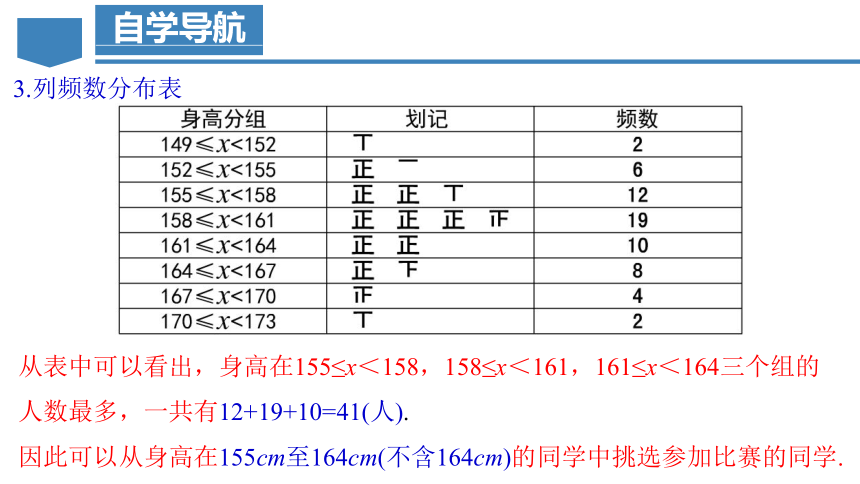
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据个数(叫做频数).
3.列频数分布表
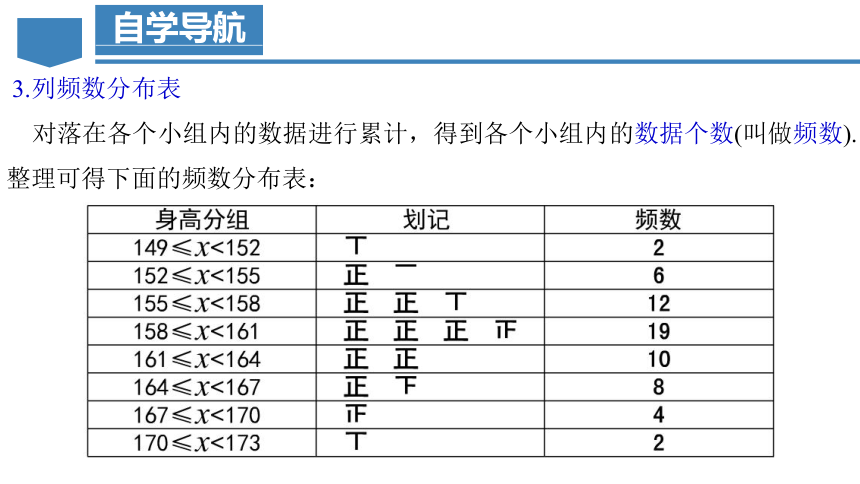
对落在各个小组内的数据进行累计,得到各个小组内的数据个数(叫做频数).整理可得下面的频数分布表:
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有12+19+10=41(人).
因此可以从身高在155cm至164cm(不含164cm)的同学中挑选参加比赛的同学.
3.列频数分布表
为了更直观形象地看出频数分布的情况,可以根据上表画出频数分布的直方图.
4.画频数分布直方图
可见,频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小,小长方形的高是频数与组距的比值.
4.画频数分布直方图
小长方形面积=组距×频数
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
4.画频数分布直方图
画频数分布直方图的一般步骤:
(1)计算最大值与最小值的差(极差)
(2)决定组距与组数:组数
(3)列频数分布表:为了数据及不重复也不遗漏,可规定各小组包括最小值不包括最大值.
(4)画频数分布直方图:在纵轴表示频数的直方图中,每个小矩形的高表示相应小组的频数.
条形统计图与频数直方图有什么区别和联系?
(1)联系--用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(2)区别--条形统计图是直观地显示出具体数据;频数直方图是表现频数的
分布情况.
(3)绘制的形式不同--条形统计图各条形分开;频数直方图的条形连在一起.
上面对数据进行分组时,组距取3,把数据分成8组.如果组距取2或4或5,可将数据分成几组?分别画出不同组距的频数分布直方图.并想一想,这样做能否选出需要的40名队员呢?
直方图的有关概念
重点
例1.(1)已知在一个样本中,40个数据分别落在4个组内,第一、二、四组数据个数分别为5,12,8,则第三组的频数为( )
A.15 B.25 C. 0.375 D. 0.6
(2)一个容量为80的数据样本,最大值为141,最小值为50,取组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
A
A
1.一组数据中的最大值是176,最小值是156,将这组数据进行分组时,取组距为3,则组数是( )
A.5 B.6 C.7 D.8
2.一个样本共有50个数据,分别落在5个小组内,第一、二、三、五小组的频数分别是2,8,15,5,则第四小组的频数是_____.
3.王老师对本班40个学生所穿校服尺码的数据统计如下:
则该班学生所穿校服尺码为“L”的有_____个.
C
20
8
例2.某工厂计划购买商家推荐试用的某品牌的分装机.试用时,设定分装的标准质量为每袋500 g,与之相差大于10 g为不合格.为检验分装效果,从分装的成品中随机抽取20袋,测得实际质量(单位:g)如下:
整理以上数据,列出每袋质量x(单位:g)的频数分布表.
频数分布表
重点
频数分布表
重点
解:计算最大值与最小值的差为513-486=27,如果组距取5,那么分成6组.列频数分布表如下:
1.小方调查了她所在班级50名同学的身高,最大值是173 cm,最小值是140 cm,绘制频数分布表时,取组距为5 cm,,则可以分成( )
A.7组 B.8组 C.9组 D.10组
2.一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为10,10,12,13,则第5组所占的百分比是______.
3.将数据83,85,87,89,84,85,86,88,87,90分组,则86.5~88.5这一组的频数是_____.
A
10%
3
4.体育委员统计了七年级(1)班全体学生一分钟跳绳的次数,并列出下面的频数分布表:
给出以下结论:
①全班共有52名学生;
②组距是20;
③组数是7;
④跳绳次数在100≤x<140范围的学生约占全
班学生的67%.
其中正确的是__________(填序号)
①②③④
例3.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%、12%、40%、28%,第五组的频数是8,则:
①该班有50名同学参赛;
②第五组的百分比为16%;
③成绩在70~80分的人数最多;
④80分以上的学生有14名.
其中正确的个数为______.
3
频数分布直方图
重点
20
1.在某次数学测验中,班长将全班50名同学的成绩(得分为整数)绘制成频数分布直方图(如图),从左到右的小长方形高的比为0.6∶2∶4 ∶2.2∶1.2,则得分在70.5到80.5之间的人数为_______.
150
2.某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了如图所示的频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为_____(注:横轴上每组数据包含最小值,不包含最大值).
140
3.某养猪场对200头生猪的质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5 kg及以上的生猪有______头.
92%
4.九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是______.
例4.为了解某地区七年级男生的身高情况,随机抽取了60名男生,测得他们的身高(单位:cm)分别是:
(1)将数据适当分组,并绘制相应的频数分布直方图;
(2)试求身高在155 ~170cm(含155cm,不含170cm)范围的男生所占的百分比.
频数分布直方图
重点
频数分布直方图
重点
解:(1)列频数分布表如下:
频数分布直方图
重点
画频数分布直方图如图所示:
(2)由图可知,身高在155~170 cm(含155 cm,不含170 cm)范围的男生有12+20+10=42(人),其所占的百分比是×100%=70%.
1.在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.某社区随机抽取了部分家庭,调查他们每月用于“信息消费”的金额x(单位:元)。将数据分组如下:A.10≤x<100;B.100≤x<200;C.200≤x<300;D.300≤x<400;E.x ≥400;并将数据整理成如图所示的不完整统计图.已知A,B两组户数在频数分布直方图中的高度比为1∶5.
请根据以上信息,解答下列问题:
(1)A 组的频数是____,本次调查
的样本容量是______;
(2)补全频数分布直方图(需标明
各组频数);
2
50
1.在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.某社区随机抽取了部分家庭,调查他们每月用于“信息消费”的金额x(单位:元)。将数据分组如下:A.10≤x<100;B.100≤x<200;C.200≤x<300;D.300≤x<400;E.x ≥400;并将数据整理成如图所示的不完整统计图.已知A,B两组户数在频数分布直方图中的高度比为1∶5.
请根据以上信息,解答下列问题:
(3)所抽取的家庭中每月用于
“信息消费”的金额不少于
200元的有_____户.
38
2.某校七年级(1)班30名学生入学时的身高(单位:cm)如表格所示:
请你根据统计表所给信息,补全频数分布表及频数分布直方图.
第10章 数据的收集、整理与描述
10.2.1 直方图(第一课时)
第六单元
1.理解频数、频率的定义; (重点)
2.频数和频率的相关计算; (难点)
3.会画简单的频数分布直方图等距分组.(难点)
你还记得各个统计图的特点吗?
折线统计图既可以反映数量的多少,更能反映数量的增减变化趋势.
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
条形统计图能清楚地表示出每个项目的具体数目.
某班一次数学测验成绩如下:
63,84,91,53,69,81,61,69
91,78,75,81,80,67,76,81
79,94,61,69,89,70,70,87
81,86,90,88,85,67,71,82
87,75,87,95,53,65,74,77
大部分同学处于哪个分数段?成绩的整体分布情况怎样?
问题:为了参加全校各年级之间的广播体操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.
为此收集到这63名同学的身高(单位:cm)如下:
选择身高在哪个范围的学生参加呢
问题:为了参加全校各年级之间的广播体操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况,即在哪些身高范围的同学比较多,而哪些身高范围的同学比较少.为此可以通过对这些数据适当分组来进行整理.
1.计算最大值与最小值的差(极差)
在上面的数据中,最小值是149,最大值是172,它们的差值为172-149=23,说明身高的变化范围是23cm.
2.决定组距和组数
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3作为一组,那么由于
= =7
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别为8和3.
2.决定组距和组数
组距和组数的确定没有固定标准,要凭借经验和所研究的具体问题来决定.将一批数据分组,一般数据越多分的组数也越多.当数据在100个以内时,按照数据的多少,常分成5~12组.
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据个数(叫做频数).
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据个数(叫做频数).整理可得下面的频数分布表:
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有12+19+10=41(人).
因此可以从身高在155cm至164cm(不含164cm)的同学中挑选参加比赛的同学.
3.列频数分布表
为了更直观形象地看出频数分布的情况,可以根据上表画出频数分布的直方图.
4.画频数分布直方图
可见,频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小,小长方形的高是频数与组距的比值.
4.画频数分布直方图
小长方形面积=组距×频数
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
4.画频数分布直方图
画频数分布直方图的一般步骤:
(1)计算最大值与最小值的差(极差)
(2)决定组距与组数:组数
(3)列频数分布表:为了数据及不重复也不遗漏,可规定各小组包括最小值不包括最大值.
(4)画频数分布直方图:在纵轴表示频数的直方图中,每个小矩形的高表示相应小组的频数.
条形统计图与频数直方图有什么区别和联系?
(1)联系--用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(2)区别--条形统计图是直观地显示出具体数据;频数直方图是表现频数的
分布情况.
(3)绘制的形式不同--条形统计图各条形分开;频数直方图的条形连在一起.
上面对数据进行分组时,组距取3,把数据分成8组.如果组距取2或4或5,可将数据分成几组?分别画出不同组距的频数分布直方图.并想一想,这样做能否选出需要的40名队员呢?
直方图的有关概念
重点
例1.(1)已知在一个样本中,40个数据分别落在4个组内,第一、二、四组数据个数分别为5,12,8,则第三组的频数为( )
A.15 B.25 C. 0.375 D. 0.6
(2)一个容量为80的数据样本,最大值为141,最小值为50,取组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
A
A
1.一组数据中的最大值是176,最小值是156,将这组数据进行分组时,取组距为3,则组数是( )
A.5 B.6 C.7 D.8
2.一个样本共有50个数据,分别落在5个小组内,第一、二、三、五小组的频数分别是2,8,15,5,则第四小组的频数是_____.
3.王老师对本班40个学生所穿校服尺码的数据统计如下:
则该班学生所穿校服尺码为“L”的有_____个.
C
20
8
例2.某工厂计划购买商家推荐试用的某品牌的分装机.试用时,设定分装的标准质量为每袋500 g,与之相差大于10 g为不合格.为检验分装效果,从分装的成品中随机抽取20袋,测得实际质量(单位:g)如下:
整理以上数据,列出每袋质量x(单位:g)的频数分布表.
频数分布表
重点
频数分布表
重点
解:计算最大值与最小值的差为513-486=27,如果组距取5,那么分成6组.列频数分布表如下:
1.小方调查了她所在班级50名同学的身高,最大值是173 cm,最小值是140 cm,绘制频数分布表时,取组距为5 cm,,则可以分成( )
A.7组 B.8组 C.9组 D.10组
2.一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为10,10,12,13,则第5组所占的百分比是______.
3.将数据83,85,87,89,84,85,86,88,87,90分组,则86.5~88.5这一组的频数是_____.
A
10%
3
4.体育委员统计了七年级(1)班全体学生一分钟跳绳的次数,并列出下面的频数分布表:
给出以下结论:
①全班共有52名学生;
②组距是20;
③组数是7;
④跳绳次数在100≤x<140范围的学生约占全
班学生的67%.
其中正确的是__________(填序号)
①②③④
例3.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%、12%、40%、28%,第五组的频数是8,则:
①该班有50名同学参赛;
②第五组的百分比为16%;
③成绩在70~80分的人数最多;
④80分以上的学生有14名.
其中正确的个数为______.
3
频数分布直方图
重点
20
1.在某次数学测验中,班长将全班50名同学的成绩(得分为整数)绘制成频数分布直方图(如图),从左到右的小长方形高的比为0.6∶2∶4 ∶2.2∶1.2,则得分在70.5到80.5之间的人数为_______.
150
2.某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了如图所示的频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为_____(注:横轴上每组数据包含最小值,不包含最大值).
140
3.某养猪场对200头生猪的质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5 kg及以上的生猪有______头.
92%
4.九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是______.
例4.为了解某地区七年级男生的身高情况,随机抽取了60名男生,测得他们的身高(单位:cm)分别是:
(1)将数据适当分组,并绘制相应的频数分布直方图;
(2)试求身高在155 ~170cm(含155cm,不含170cm)范围的男生所占的百分比.
频数分布直方图
重点
频数分布直方图
重点
解:(1)列频数分布表如下:
频数分布直方图
重点
画频数分布直方图如图所示:
(2)由图可知,身高在155~170 cm(含155 cm,不含170 cm)范围的男生有12+20+10=42(人),其所占的百分比是×100%=70%.
1.在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.某社区随机抽取了部分家庭,调查他们每月用于“信息消费”的金额x(单位:元)。将数据分组如下:A.10≤x<100;B.100≤x<200;C.200≤x<300;D.300≤x<400;E.x ≥400;并将数据整理成如图所示的不完整统计图.已知A,B两组户数在频数分布直方图中的高度比为1∶5.
请根据以上信息,解答下列问题:
(1)A 组的频数是____,本次调查
的样本容量是______;
(2)补全频数分布直方图(需标明
各组频数);
2
50
1.在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.某社区随机抽取了部分家庭,调查他们每月用于“信息消费”的金额x(单位:元)。将数据分组如下:A.10≤x<100;B.100≤x<200;C.200≤x<300;D.300≤x<400;E.x ≥400;并将数据整理成如图所示的不完整统计图.已知A,B两组户数在频数分布直方图中的高度比为1∶5.
请根据以上信息,解答下列问题:
(3)所抽取的家庭中每月用于
“信息消费”的金额不少于
200元的有_____户.
38
2.某校七年级(1)班30名学生入学时的身高(单位:cm)如表格所示:
请你根据统计表所给信息,补全频数分布表及频数分布直方图.
