10.2.2 直方图(第二课时) 课件(共23张PPT)
文档属性
| 名称 | 10.2.2 直方图(第二课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
第10章 数据的收集、整理与描述
10.2.2 直方图(2)
第六单元
1.明确频数直方图制作的步骤,会绘制频数直方图;(难点)
2.能从频数分布表和频数直方图中获取有关信息,作出合理的判断和预测.
(重点)
画频数分布直方图的一般步骤:
(1)计算最大值与最小值的差(极差)
(2)决定组距与组数:组数
(3)列频数分布表:为了数据及不重复也不遗漏,可规定各小组包括最小值不包括最大值.
(4)画频数分布直方图:在纵轴表示频数的直方图中,每个小矩形的高表示相应小组的频数.
某校24名男教师的年龄(岁)如下:
29 42 28 37 33 52 26 31 33 24 37 42
46 40 32 42 28 38 30 51 32 44 30 31
(1)填写表格:
(2)这组数据的最大值与最小值的差
为___,所取组距是___,共分___组.
28
5
6
频数分布直方图的应用
重点
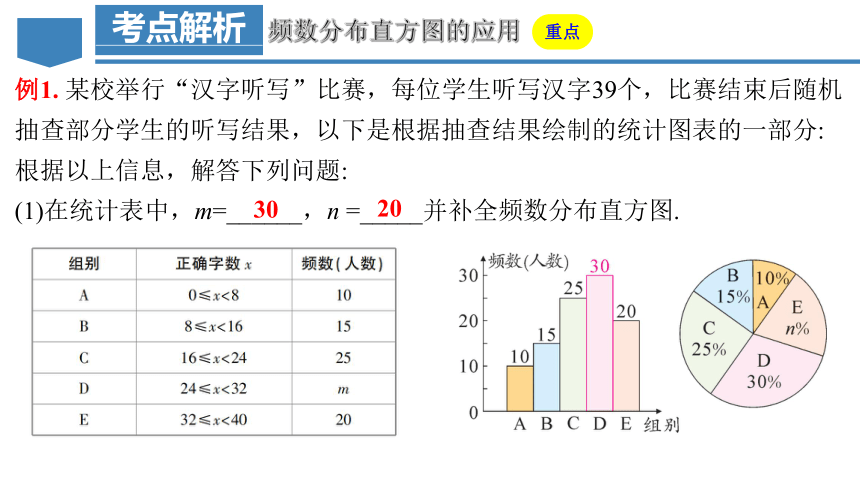
例1. 某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图表的一部分:
根据以上信息,解答下列问题:
(1)在统计表中,m=______,n =_____并补全频数分布直方图.
30
20
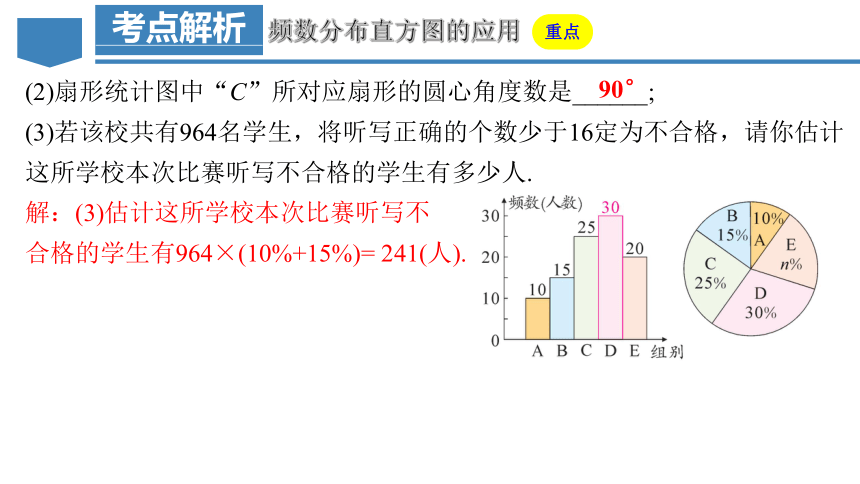
(2)扇形统计图中“C”所对应扇形的圆心角度数是______;
(3)若该校共有964名学生,将听写正确的个数少于16定为不合格,请你估计这所学校本次比赛听写不合格的学生有多少人.
解:(3)估计这所学校本次比赛听写不
合格的学生有964×(10%+15%)= 241(人).
90°
频数分布直方图的应用
重点
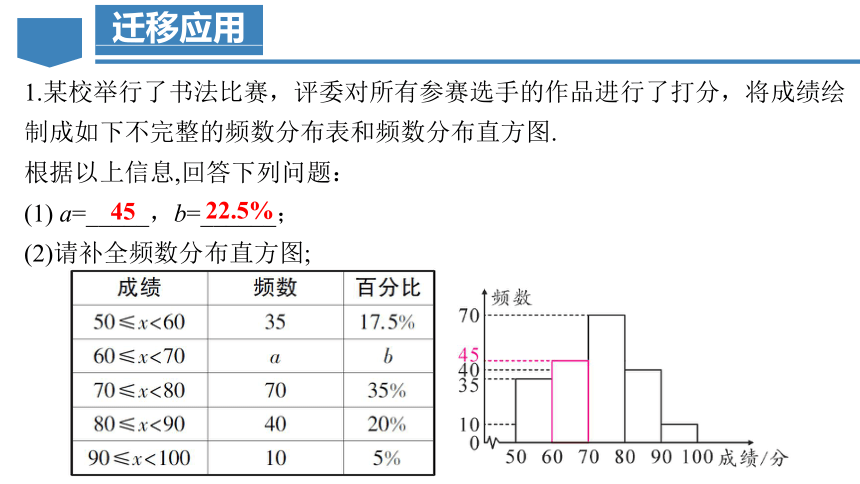
1.某校举行了书法比赛,评委对所有参赛选手的作品进行了打分,将成绩绘制成如下不完整的频数分布表和频数分布直方图.
根据以上信息,回答下列问题:
(1) a=_____,b=______;
(2)请补全频数分布直方图;
45
22.5%
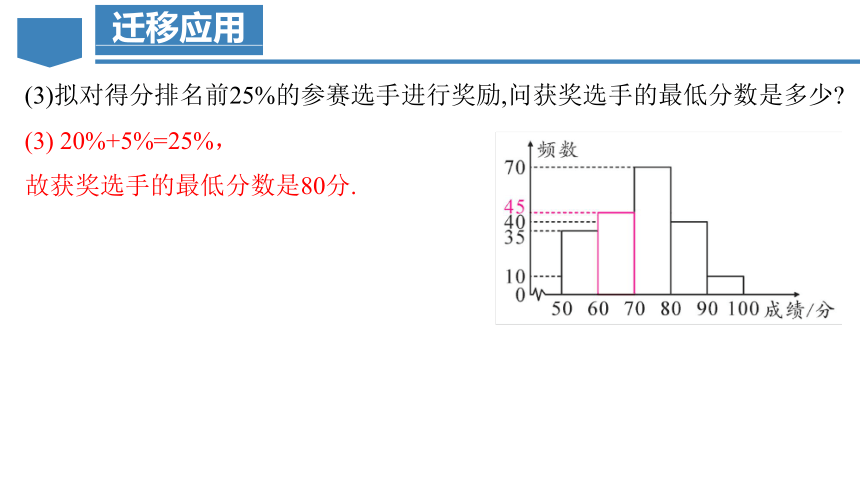
(3)拟对得分排名前25%的参赛选手进行奖励,问获奖选手的最低分数是多少
(3) 20%+5%=25%,
故获奖选手的最低分数是80分.
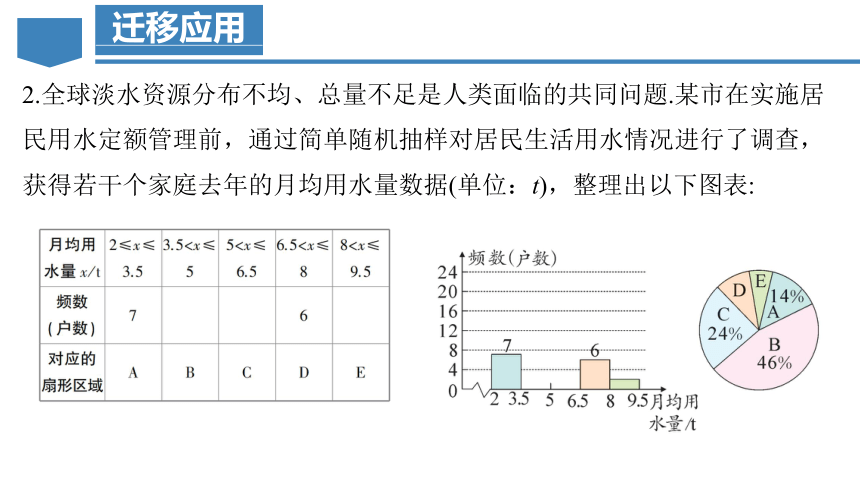
2.全球淡水资源分布不均、总量不足是人类面临的共同问题.某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得若干个家庭去年的月均用水量数据(单位:t),整理出以下图表:
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并求出扇形统计
图中扇形E对应的圆心角度数.
解:(1)抽取的家庭总数为7÷14%=50.
B对应的频数为50×46%=23,
C对应的频数为50×24%=12,
E对应的频数为50-7-23-12-6=2.
扇形统计图中扇形E对应的圆心角度数为×360°=14.4°.
(2)为鼓励节约用水,要确定一个月用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少 并说明理由.
(2)要使60%的家庭水费支出不受影响,家庭月均用水量应该定为5t.
理由如下:根据扇形统计图可知,月均用水量不超过5 t的家庭占比为14%+46%=60%.
频数分布直方图的应用
重点
例2.为了控制学生的书面作业量,规范中小学生的作息时间,某中学随机抽查部分学生,调查他们平均每天的作业时间,以下是根据抽查结果绘制的统计图表的一部分:
请结合图表回答下列问题:
(1)在统计表中,m=_____,n=_____;
(2)扇形统计图中“B组”对应扇形的圆心角的度数α=_____;
(3)请你补全频数分布直方图;
72°
2
20
频数分布直方图的应用
重点
频数分布直方图的应用
重点
(4)若该校共有750名学生,当平均每天作业时间在1.5 h以内时,说明作业量对该生比较适中,请你估算这所学校作业量适中的学生人数.
解: (4) 750×=480(名).
答:估算这所掌校作止量适中的学生
人数为480.
1.为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
10
25
0.25
⑴填空:a=_____,b=____,n=_____.
⑵将频数分布直方图补充完整;
(3)该校对考试成绩为91≤x≤100 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1∶3∶6,请你估算全校获得二等奖的学生人数.
解:2500××=90(人).
答:估计全校获得二等奖的学生人数为90.
2.为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分钟跳绳次数的测试,并把测得的数据分成四组,绘制成如图所示的频数分布表和未完成的频数分布直方图(每一组不含前一个边界值,含后一个边界值).
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求该年级一分钟跳绳次数在190以上的学生数占该年级全部学生数的百分比.
解:(1)a=360-(48+96+72)=144.
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求该年级一分钟跳绳次数在190以上的学生数占该年级全部学生数的百分比.
解:(1)a=360-(48+96+72)=144.
(3)该年级一分钟跳兔次数在190 以上的学生数占该年级全部学生数的百分比为×100%= 20%.
3.为了解某校某年级1000名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过150次),整理后绘制成如图的频数分布直方图,图中的a,b满足关系式2a=3b.后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.
(1)求问题中的总体和样本容量;
解:1000名学生一分钟的跳绳次数的全体是总体,样本容量是40.
(2)求a,b的值(请写出必要的计算过程);
解:由题意所给数据可知,50.5~75.5的有4人,75.5~100.5的有16人,
所以a+b=40-4-16=20
因为2a=3b,
所以联立
解得
(3)如果一分钟跳绳次数在125次以上(不含125次)为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的人数是多少(注:该年级共1000名学生)
解:1000×=200(人).
答:估计该校该年级学生跳绳成绩优秀的人数是200.
第10章 数据的收集、整理与描述
10.2.2 直方图(2)
第六单元
1.明确频数直方图制作的步骤,会绘制频数直方图;(难点)
2.能从频数分布表和频数直方图中获取有关信息,作出合理的判断和预测.
(重点)
画频数分布直方图的一般步骤:
(1)计算最大值与最小值的差(极差)
(2)决定组距与组数:组数
(3)列频数分布表:为了数据及不重复也不遗漏,可规定各小组包括最小值不包括最大值.
(4)画频数分布直方图:在纵轴表示频数的直方图中,每个小矩形的高表示相应小组的频数.
某校24名男教师的年龄(岁)如下:
29 42 28 37 33 52 26 31 33 24 37 42
46 40 32 42 28 38 30 51 32 44 30 31
(1)填写表格:
(2)这组数据的最大值与最小值的差
为___,所取组距是___,共分___组.
28
5
6
频数分布直方图的应用
重点
例1. 某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图表的一部分:
根据以上信息,解答下列问题:
(1)在统计表中,m=______,n =_____并补全频数分布直方图.
30
20
(2)扇形统计图中“C”所对应扇形的圆心角度数是______;
(3)若该校共有964名学生,将听写正确的个数少于16定为不合格,请你估计这所学校本次比赛听写不合格的学生有多少人.
解:(3)估计这所学校本次比赛听写不
合格的学生有964×(10%+15%)= 241(人).
90°
频数分布直方图的应用
重点
1.某校举行了书法比赛,评委对所有参赛选手的作品进行了打分,将成绩绘制成如下不完整的频数分布表和频数分布直方图.
根据以上信息,回答下列问题:
(1) a=_____,b=______;
(2)请补全频数分布直方图;
45
22.5%
(3)拟对得分排名前25%的参赛选手进行奖励,问获奖选手的最低分数是多少
(3) 20%+5%=25%,
故获奖选手的最低分数是80分.
2.全球淡水资源分布不均、总量不足是人类面临的共同问题.某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得若干个家庭去年的月均用水量数据(单位:t),整理出以下图表:
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并求出扇形统计
图中扇形E对应的圆心角度数.
解:(1)抽取的家庭总数为7÷14%=50.
B对应的频数为50×46%=23,
C对应的频数为50×24%=12,
E对应的频数为50-7-23-12-6=2.
扇形统计图中扇形E对应的圆心角度数为×360°=14.4°.
(2)为鼓励节约用水,要确定一个月用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少 并说明理由.
(2)要使60%的家庭水费支出不受影响,家庭月均用水量应该定为5t.
理由如下:根据扇形统计图可知,月均用水量不超过5 t的家庭占比为14%+46%=60%.
频数分布直方图的应用
重点
例2.为了控制学生的书面作业量,规范中小学生的作息时间,某中学随机抽查部分学生,调查他们平均每天的作业时间,以下是根据抽查结果绘制的统计图表的一部分:
请结合图表回答下列问题:
(1)在统计表中,m=_____,n=_____;
(2)扇形统计图中“B组”对应扇形的圆心角的度数α=_____;
(3)请你补全频数分布直方图;
72°
2
20
频数分布直方图的应用
重点
频数分布直方图的应用
重点
(4)若该校共有750名学生,当平均每天作业时间在1.5 h以内时,说明作业量对该生比较适中,请你估算这所学校作业量适中的学生人数.
解: (4) 750×=480(名).
答:估算这所掌校作止量适中的学生
人数为480.
1.为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
10
25
0.25
⑴填空:a=_____,b=____,n=_____.
⑵将频数分布直方图补充完整;
(3)该校对考试成绩为91≤x≤100 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1∶3∶6,请你估算全校获得二等奖的学生人数.
解:2500××=90(人).
答:估计全校获得二等奖的学生人数为90.
2.为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分钟跳绳次数的测试,并把测得的数据分成四组,绘制成如图所示的频数分布表和未完成的频数分布直方图(每一组不含前一个边界值,含后一个边界值).
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求该年级一分钟跳绳次数在190以上的学生数占该年级全部学生数的百分比.
解:(1)a=360-(48+96+72)=144.
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求该年级一分钟跳绳次数在190以上的学生数占该年级全部学生数的百分比.
解:(1)a=360-(48+96+72)=144.
(3)该年级一分钟跳兔次数在190 以上的学生数占该年级全部学生数的百分比为×100%= 20%.
3.为了解某校某年级1000名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过150次),整理后绘制成如图的频数分布直方图,图中的a,b满足关系式2a=3b.后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.
(1)求问题中的总体和样本容量;
解:1000名学生一分钟的跳绳次数的全体是总体,样本容量是40.
(2)求a,b的值(请写出必要的计算过程);
解:由题意所给数据可知,50.5~75.5的有4人,75.5~100.5的有16人,
所以a+b=40-4-16=20
因为2a=3b,
所以联立
解得
(3)如果一分钟跳绳次数在125次以上(不含125次)为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的人数是多少(注:该年级共1000名学生)
解:1000×=200(人).
答:估计该校该年级学生跳绳成绩优秀的人数是200.
