第8章 幂的运算(章末复习)-七年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 第8章 幂的运算(章末复习)-七年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览





文档简介
第8章 幂的运算
章末复习
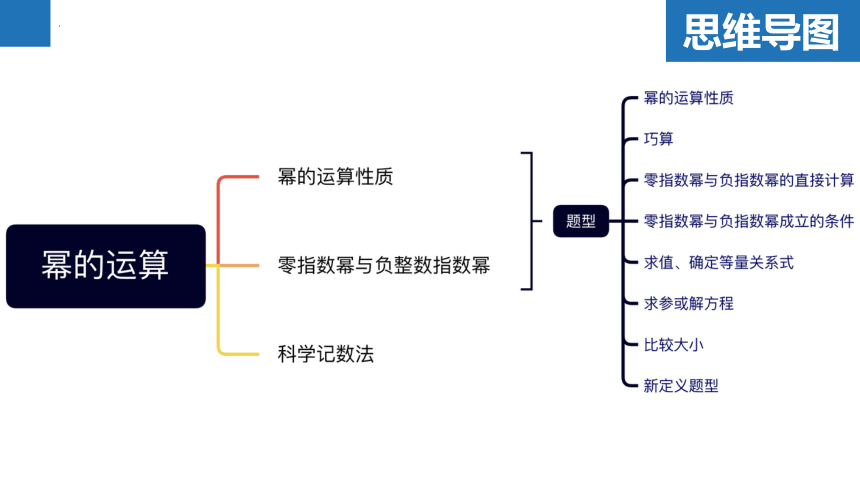
思维导图
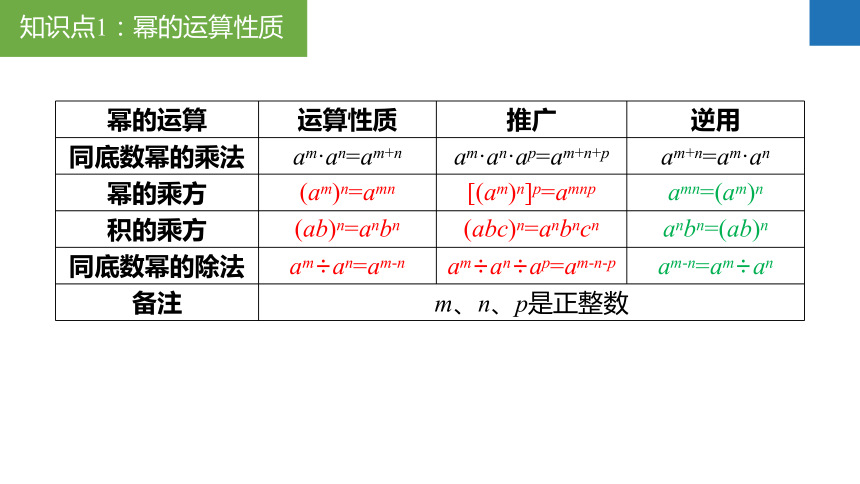
知识点1:幂的运算性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}幂的运算
运算性质
推广
逆用
同底数幂的乘法
am·an=am+n
am·an·ap=am+n+p
am+n=am·an
幂的乘方
积的乘方
同底数幂的除法
备注
m、n、p是正整数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(am)n=amn
[(am)n]p=amnp
amn=(am)n
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(ab)n=anbn
(abc)n=anbncn
anbn=(ab)n
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}am÷an=am-n
am÷an÷ap=am-n-p
am-n=am÷an
例1-1、下列计算正确的是( )
A.x4+x2=x2 B.(-3xy)2=6x2y2
C.y2·y3=y5 D.(a6)2÷(a4)3=a
【分析】
B.(-3xy)2=9x2y2;
D.(a6)2÷(a4)3=a0=1。
典例精析
C
例1-2、0.752024×42025×(-????????)2026。
?
典例精析——巧算
解:原式=(-0.75×4×????????)2024×4×(-????????)2
=(-0.75×4×????????)2024×4×????????
=(-1)2024×4×????????
=1×4×????????
=????????。
?
例1-3、(1)已知2a=x,2b=y,求42a+3b的值;
(2)已知4a-3b-3=0,求52×252a÷125b+1的值。
典例精析——求值
【分析】
(1)42a+3b=42a×43b=24a×26b=(2a)4×(2b)6=x4y6;
(2)52×252a÷125b+1=52×54a÷53b+3=52+4a-(3b+3)=54a-3b-1=52=25。
例1-4、(1)已知16x=a,4y=b,64z=ab,那么x、y、z满足的等量关系是____________;
(2)如果x=3m+1,y=2-9m,那么用x的代数式表示y为____________。
典例精析——确定等量关系式
【分析】
(1)∵16x=a,4y=b,64z=ab,
∴16x·4y=64z,即42x·4y=43z,
∴42x+y=43z,即2x+y=3z;
2x+y=3z
(2)∵x=3m+1,y=2-9m,
∴3m=x-1,
∴y=2-(3m)2=2-(x-1)2=-x2+2x+1。
y=-x2+2x+1
例1-5、(1)已知2x·43-x·81+x=32,求x的值;
(2)已知2x+2·5x+2=103x-4,求x的值。
典例精析——求参或解方程
(2)2x+2·5x+2=(2×5)x+2=10x+2=103x-4,
即x+2=3x-4,解得:x=3。
【分析】
(1)2x·43-x·81+x=2x·26-2x·23+3x=2x+6-2x+3+3x=22x+9=25,
即2x+9=5,解得:x=-2;
例1-6、(1)比较914与279的大小;
(2)已知a=255,b=344,c=622,则a、b、c的大小关系是________(请用字母表示,并用“<”连接)。
典例精析——比较大小
【分析】(1)∵914=(32)14=328,279=(33)9=327,
∴328>327,∴914>279;
(2)∵a=255=(25)11=3211,b=344=(34)11=8111,c=622=(62)11=3611,
∴3211<3611<8111,∴aa知识点2:零指数幂与负整数指数幂
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
运算性质
成立的条件
逆用
零指数幂
负整数指数幂
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a0=1
a≠0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a-n=
a≠0,n是正整数
=a-n
例2-1、计算:-12025+(????????)-3+(π-3)0-|-4|。
?
解:原式=-1+64+1-4
=60。
典例精析
例2-2、若(x-3)0 -2(2x-4)-1有意义,则x的取值范围是____________。
x≠3且x≠2
典例精析——成立的条件
【分析】
由题意可得:x-3≠0且2x-4≠0,
∴x≠3且x≠2。
例2-3、若(2-x)????????-4=1,则x的值为________。
?
【分析】
①x2-4=0且2-x=0,解得:x=-2;
②2-x=1,解得:x=1;
③2-x=-1且x2-4为偶数,无解。
-2或1
典例精析——求值
例2-4、已知9m÷32m+2=(????????)n,求n的值。
?
典例精析——求参或解方程
【分析】
9m÷32m+2=32m÷32m+2=32m-(2m+2)=3-2=(????????)n=3-n,
即-2=-n,解得:n=2。
?
例2-5、已知如果a=(-99)0,b=(-0.1)-1,c=(-????????)-2,那么a、b、c的大小关系为________(请用字母表示,并用“>”连接)。
?
典例精析——比较大小
【分析】
∵a=(-99)0 =1,b=(-0.1)-1=-10,c=(-????????)-2=????????????,
∴1>????????????>-10,∴a>c>b。
?
a>c>b
知识点3:科学记数法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
有关概念
科学记数法
纳米
一般地,用科学记数法可以把一个正数写成a×10n的形式,其中1≤a<10,n是整数
纳米是长度单位,1nm=10-9m
例3、细菌、病毒、支原体感染都会引起呼吸系统感染。其中,支原体是比细菌小,比病毒大的微生物,直径在150~300nm,150nm用科学记数法表示为(1nm=10-9m)( )
A.150×10-9m B.1.50×10-6m
C.1.50×10-7m D.1.50×10-8m
【分析】150nm=150×10-9m=1.50×10-7m。
典例精析
C
章末复习
思维导图
知识点1:幂的运算性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}幂的运算
运算性质
推广
逆用
同底数幂的乘法
am·an=am+n
am·an·ap=am+n+p
am+n=am·an
幂的乘方
积的乘方
同底数幂的除法
备注
m、n、p是正整数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(am)n=amn
[(am)n]p=amnp
amn=(am)n
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(ab)n=anbn
(abc)n=anbncn
anbn=(ab)n
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}am÷an=am-n
am÷an÷ap=am-n-p
am-n=am÷an
例1-1、下列计算正确的是( )
A.x4+x2=x2 B.(-3xy)2=6x2y2
C.y2·y3=y5 D.(a6)2÷(a4)3=a
【分析】
B.(-3xy)2=9x2y2;
D.(a6)2÷(a4)3=a0=1。
典例精析
C
例1-2、0.752024×42025×(-????????)2026。
?
典例精析——巧算
解:原式=(-0.75×4×????????)2024×4×(-????????)2
=(-0.75×4×????????)2024×4×????????
=(-1)2024×4×????????
=1×4×????????
=????????。
?
例1-3、(1)已知2a=x,2b=y,求42a+3b的值;
(2)已知4a-3b-3=0,求52×252a÷125b+1的值。
典例精析——求值
【分析】
(1)42a+3b=42a×43b=24a×26b=(2a)4×(2b)6=x4y6;
(2)52×252a÷125b+1=52×54a÷53b+3=52+4a-(3b+3)=54a-3b-1=52=25。
例1-4、(1)已知16x=a,4y=b,64z=ab,那么x、y、z满足的等量关系是____________;
(2)如果x=3m+1,y=2-9m,那么用x的代数式表示y为____________。
典例精析——确定等量关系式
【分析】
(1)∵16x=a,4y=b,64z=ab,
∴16x·4y=64z,即42x·4y=43z,
∴42x+y=43z,即2x+y=3z;
2x+y=3z
(2)∵x=3m+1,y=2-9m,
∴3m=x-1,
∴y=2-(3m)2=2-(x-1)2=-x2+2x+1。
y=-x2+2x+1
例1-5、(1)已知2x·43-x·81+x=32,求x的值;
(2)已知2x+2·5x+2=103x-4,求x的值。
典例精析——求参或解方程
(2)2x+2·5x+2=(2×5)x+2=10x+2=103x-4,
即x+2=3x-4,解得:x=3。
【分析】
(1)2x·43-x·81+x=2x·26-2x·23+3x=2x+6-2x+3+3x=22x+9=25,
即2x+9=5,解得:x=-2;
例1-6、(1)比较914与279的大小;
(2)已知a=255,b=344,c=622,则a、b、c的大小关系是________(请用字母表示,并用“<”连接)。
典例精析——比较大小
【分析】(1)∵914=(32)14=328,279=(33)9=327,
∴328>327,∴914>279;
(2)∵a=255=(25)11=3211,b=344=(34)11=8111,c=622=(62)11=3611,
∴3211<3611<8111,∴a
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
运算性质
成立的条件
逆用
零指数幂
负整数指数幂
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a0=1
a≠0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a-n=
a≠0,n是正整数
=a-n
例2-1、计算:-12025+(????????)-3+(π-3)0-|-4|。
?
解:原式=-1+64+1-4
=60。
典例精析
例2-2、若(x-3)0 -2(2x-4)-1有意义,则x的取值范围是____________。
x≠3且x≠2
典例精析——成立的条件
【分析】
由题意可得:x-3≠0且2x-4≠0,
∴x≠3且x≠2。
例2-3、若(2-x)????????-4=1,则x的值为________。
?
【分析】
①x2-4=0且2-x=0,解得:x=-2;
②2-x=1,解得:x=1;
③2-x=-1且x2-4为偶数,无解。
-2或1
典例精析——求值
例2-4、已知9m÷32m+2=(????????)n,求n的值。
?
典例精析——求参或解方程
【分析】
9m÷32m+2=32m÷32m+2=32m-(2m+2)=3-2=(????????)n=3-n,
即-2=-n,解得:n=2。
?
例2-5、已知如果a=(-99)0,b=(-0.1)-1,c=(-????????)-2,那么a、b、c的大小关系为________(请用字母表示,并用“>”连接)。
?
典例精析——比较大小
【分析】
∵a=(-99)0 =1,b=(-0.1)-1=-10,c=(-????????)-2=????????????,
∴1>????????????>-10,∴a>c>b。
?
a>c>b
知识点3:科学记数法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
有关概念
科学记数法
纳米
一般地,用科学记数法可以把一个正数写成a×10n的形式,其中1≤a<10,n是整数
纳米是长度单位,1nm=10-9m
例3、细菌、病毒、支原体感染都会引起呼吸系统感染。其中,支原体是比细菌小,比病毒大的微生物,直径在150~300nm,150nm用科学记数法表示为(1nm=10-9m)( )
A.150×10-9m B.1.50×10-6m
C.1.50×10-7m D.1.50×10-8m
【分析】150nm=150×10-9m=1.50×10-7m。
典例精析
C
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
