第10章 轴对称、平移与旋转 导学案
图片预览


文档简介
10.1轴对称(1)
课 题 10.1.1 生活中的轴对称 课 型 第一课时
策划者 审核者 导学者
学习时间 学习者 班 级
学习目标 (1)通过生活中的轴对称现象,了解轴对称图形及轴对称的区别与联系;(2)加深这两个概念的理解,能正确识别轴对称图形,培养观察能力;(3)体会轴对称在现实生活中的广泛运用和它的美学价值;
学习重点 轴对称图形的概念.
学习难点 判断图形是否是轴对称图形
教学准备 三角尺
激趣明标 1.观察一下书P98中的图形,它们都是 ( )图形,这些图形有什么特点呢?(让学生说一说) 2、轴对称图形的定义: 如果一个图形沿某条直线对折,对折两部分( ),那么这个图形 ( ),这条直线叫做这个图形的 ( )。3、画出书中图10.1.1中各图形的对称轴。是不是每一个轴对称图形都只有一条对称轴?答: 。
自主学习 自学教材99-100页轴对称的定义:把一个图形沿着某一条直线翻折过去,如果它能够与( )重合,那么就说这两个图形( ),这条直线就是( ) ,两个图形中的对应点(即两个图形重合时互相重合的点)叫做( )。5、轴对称图形和轴对称的区别与联系 区别:(1)轴对称图形是指一个具有特殊形状的图形,只对( )个 图形而言;轴对称是指( )个图形的位置的关系,必须涉及( )个图形。(2)轴对称图形的对称轴( );轴对称只有 ( )。 联系:(1)图中都有一条直线,都要沿着这条直线 。(2)如果把两个成轴对称图形拼在一起,看成一个整体,那么它就是一个 。如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成( )。 (3)轴对称图形(或关于某条直线对称的两个图形)沿对称轴对折后的两部分是 的,所以它的对应线段(对折后重合的线段)( ),对应角(对折后重合的角)( )。
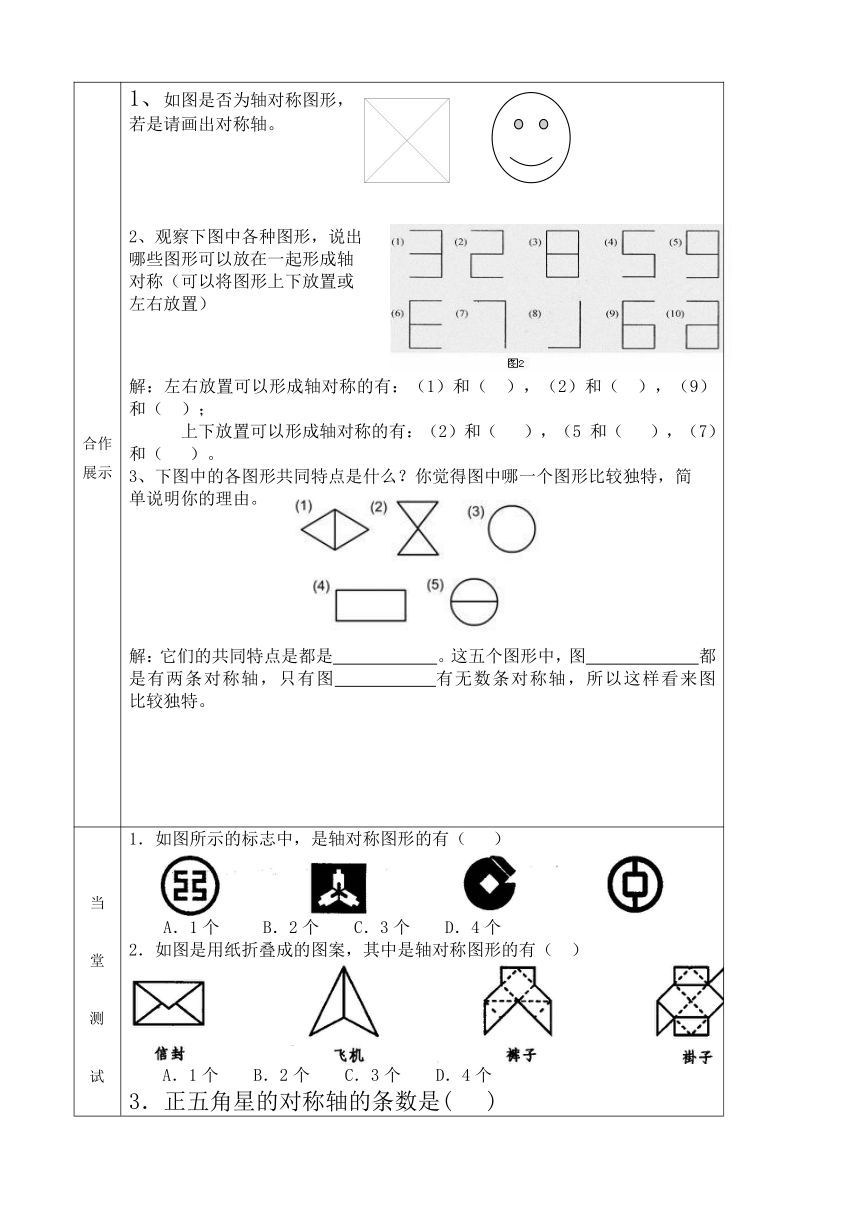
合作展示 1、如图是否为轴对称图形,若是请画出对称轴。 2、观察下图中各种图形,说出哪些图形可以放在一起形成轴对称(可以将图形上下放置或左右放置)解:左右放置可以形成轴对称的有:(1)和( ),(2)和( ),(9)和( ); 上下放置可以形成轴对称的有:(2)和( ),(5 和( ),(7)和( )。3、下图中的各图形共同特点是什么?你觉得图中哪一个图形比较独特,简单说明你的理由。解:它们的共同特点是都是 。这五个图形中,图 都是有两条对称轴,只有图 有无数条对称轴,所以这样看来图 比较独特。
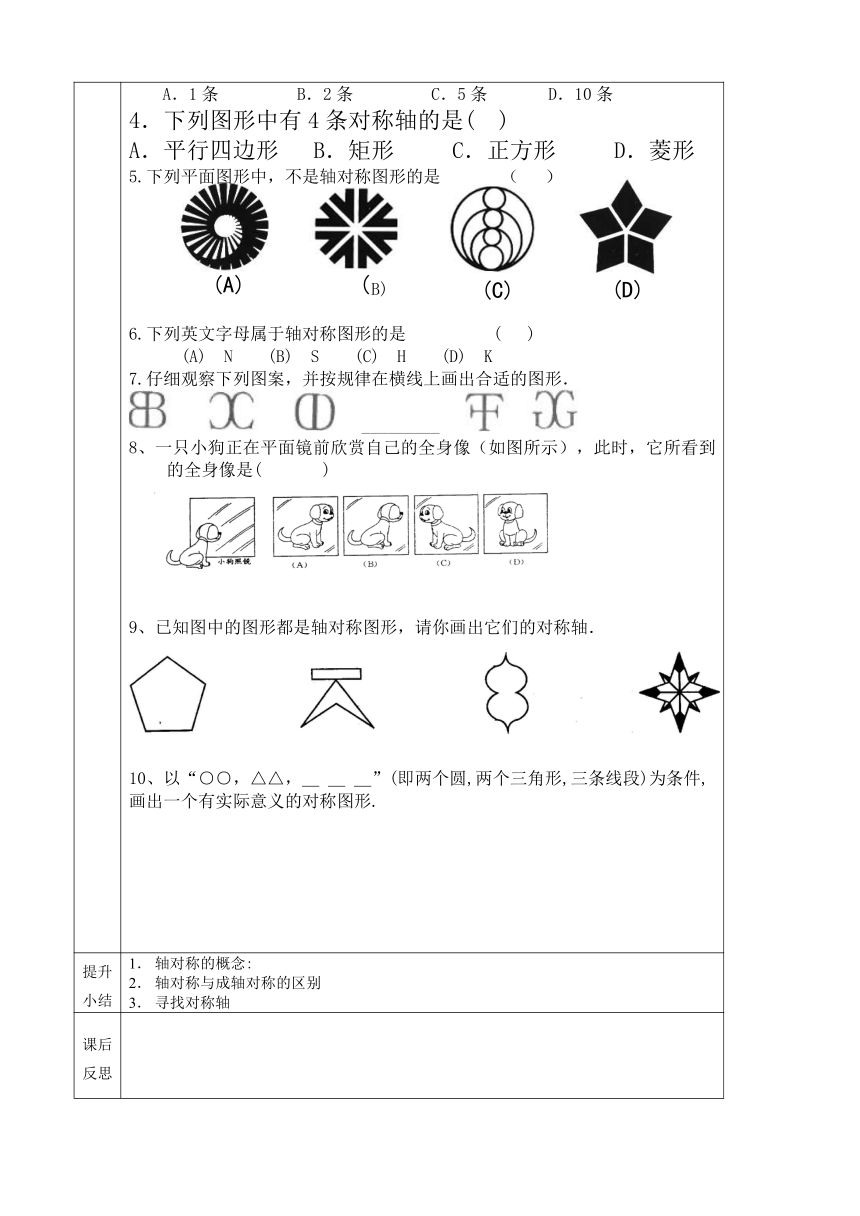
当堂测试 1.如图所示的标志中,是轴对称图形的有( ) A.1个 B.2个 C.3个 D.4个2.如图是用纸折叠成的图案,其中是轴对称图形的有( )A.1个 B.2个 C.3个 D.4个3.正五角星的对称轴的条数是( )A.1条 B.2条 C.5条 D.10条4.下列图形中有4条对称轴的是( )A.平行四边形 B.矩形 C.正方形 D.菱形5.下列平面图形中,不是轴对称图形的是 ( ) B)6.下列英文字母属于轴对称图形的是 ( )(A) N (B) S (C) H (D) K7.仔细观察下列图案,并按规律在横线上画出合适的图形. _________ 8、一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时,它所看到的全身像是( )9、已知图中的图形都是轴对称图形,请你画出它们的对称轴.10、以“○○,△△,_ _ _”(即两个圆,两个三角形,三条线段)为条件,画出一个有实际意义的对称图形. ( http: / / www. )
提升小结 轴对称的概念:轴对称与成轴对称的区别寻找对称轴
课后反思
第2课时 轴对称的再认识
课题 轴对称的再认识 课型 第二课时
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.探索线段、角的轴对称性。2.会找图形的对称轴。
学习重点 探索线段、角的轴对称性
学习难点 找已知图形的对称轴
教学准备 三角尺
激趣明标 1.什么叫轴对称?什么叫对称轴? 2.我们上期学过的线段和角是轴对称图形吗,你能找出对称轴吗?
自主学习 一、 探索线段、角的轴对称性1.探索线段的轴对性(1)动手做一做:在纸上画出线段AB及它的中点O,再过点O画出与AB垂直的直线CD,沿直线CD将纸对折,看看线段OA与OB是否能够重合?(2)从上面的操作你可以看出线段是 图形,它的对称轴是 。2.探索角的轴对称性(1)动手做一做:在纸上画出∠AOB,对折,使角的两边完全重合,然后用直尺画出折痕OM,看看射线OM与∠AOB 是什么关系?(2)从上面的操作可以看出,角是 图形,它的对称轴是 。(注意对称轴描述时的准确性)
合作展示 找图形的对称轴(1)阅读P102--P103的内容(从第二个“试一试”开始,读完第二个“做一做”),完成课本及云图中的问题。并归纳出画复杂的轴对称图形的对称轴的步骤。(2)你还能找到其他画轴对称图形的对称轴的方法吗?(3)通过以上的操作,可以得到:如果一个图形是轴对称图形,那么 是该图形的对称轴。这也是轴对称图形的一个重要性质。
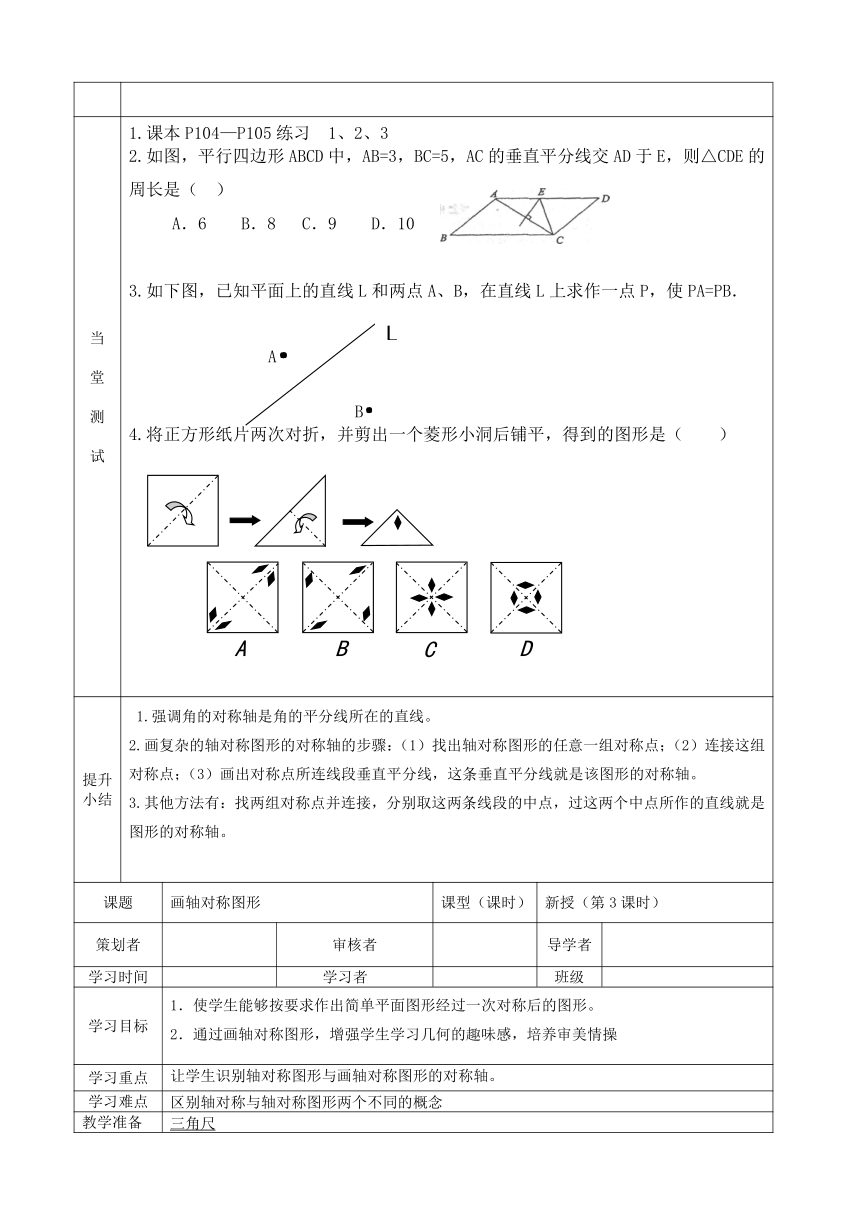
当堂测试 1.课本P104—P105练习 1、2、32.如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( )A.6 B.8 C.9 D.103.如下图,已知平面上的直线L和两点A、B,在直线L上求作一点P,使PA=PB.AB4.将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是( )
提升小结 1.强调角的对称轴是角的平分线所在的直线。2.画复杂的轴对称图形的对称轴的步骤:(1)找出轴对称图形的任意一组对称点;(2)连接这组对称点;(3)画出对称点所连线段垂直平分线,这条垂直平分线就是该图形的对称轴。3.其他方法有:找两组对称点并连接,分别取这两条线段的中点,过这两个中点所作的直线就是图形的对称轴。
课题 画轴对称图形 课型(课时) 新授(第3课时)
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.使学生能够按要求作出简单平面图形经过一次对称后的图形。 2.通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操
学习重点 让学生识别轴对称图形与画轴对称图形的对称轴。
学习难点 区别轴对称与轴对称图形两个不同的概念
教学准备 三角尺
激趣明标 叫做轴对称图形。怎样寻找对称轴
自主学习 如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢 请同学们尝试解决以下问题:如图(1),(2)实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形。 3、如图,已知点A和L直线,试画出点A关于直线l的对称点A′。 LA· 4、请你画出图中A、B、C三点关于直线l的对称点。 AB C
合作展示 1.已知△ABC,直线L,画出△ABC关于直线L的对称图形。 A B C 2、在图中分别画出点A关于两条直线的对称点和点.3、 画出所示图形关于直线的对称图形.
当堂测试 1、填空:(1)、圆有 对称轴。(2)、正方形有 条对称轴,长方形有 条对称轴,等腰三角形有 条对称轴,等边三角形有 条对称轴。2、如图,分别以AB为对称轴,画出各图形的对称图形,并观察图形(3)和它的轴对称图形构成一个 三角形.3、一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 。4、星期天小华去书店买书时,从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)的位置如图所示,此时时针表示的时间是 。5、下列图形中,是轴对称图形的是( )6、从A地到河边取水后返回B地,如何走路程最短?请作图示意。
提升小结 谈谈自己对这节课的感受,教师点评各个小组的表现。
课后反思
第4课时 设计轴对称图案
课题 设计轴对称图案 课型(课时) 新授(第4课时)
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.使学生能设计简单的轴对称图案。 2.使学生能够欣赏现实生活中的轴对称图形。
学习重点 利用对称轴进行图案设计。
学习难点 寻找对称轴以及如何利用对称轴作轴对称图形。
教学准备
激趣明标 1.如图(1),请画出△ABC的关于直线l对称的图形。 A A l B C B C 图(1) 图(2)2.如图(2),等边△ABC是轴对称图形吗 如果是,它有几条对称轴 画画试试看。
自主学习 在日常生活中,我们可以看到丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中有许多轴对称图形。请同学们欣赏P107页四个装饰图案。如图(3)是一个轴对称图形。 问:1.有多少条对称轴呢 2.可以利用轴对称性来画出它吗 请准备一张正方形纸片,按以下5个步骤一起来画。 (1)在正方形纸片上画出四条对称轴。 (2)在其中一个三角形中,如图,画出图形形状的基本线条。(注意:不同的线条最终会得到不同的图案,你可以自己设计线条,而不必和书上一样。) (3)按照其中一条斜的对称轴画出(2)中图形的对称图形。 (4)按照另一条斜的对称轴画出(3)中图形的对称图形。 (5)按照水平(或垂直)对称画出(4)中图形的对称图形,即得到图(3)中的图。 在图案上涂上你喜欢的颜色,擦掉其他的线条,轴对称的图案就完成了。
合作展示 图15—4—9中各图是只有一条对称轴的图形,请你涂黑图形的一部分,使它成为具有两条对称轴的图形.下面各图是只有一条对称轴的图形,请你涂黑图形的一部分,使它成为具有两条对称轴的图形.图15—4—9图15—4—1
当堂测试 一、选择题1.下列命题中,正确的是( )A.两个全等的三角形合在一起是一个轴对称图形B.等腰三角形的对称轴是底边上的中线C.等腰三角形底边上的高就是底边的垂直平分线D.一条线段可以看做以它的垂直平分线为轴的轴对称图形2.下列说法中,正确的是( )A.两个全等三角形,一定是轴对称的B.两个轴对称的三角形,一定是全等的C.三角形的一条中线把三角形分成以中线为轴对称的两个图形D.三角形的一条高把三角形分成以高线为轴对称的两个图形3.在直线、线段、角、两条平行直线、两条相交直线这些图形中,是轴对称图形的有( )A.5个 B.4个 C.3个 D.2个4.如图15—4—6,△ABC和△A'B'C'关于直线l对称,下列结论中:①△ABC△A'B'C';②∠BAC'=∠B'AC;③l垂直平分CC';④直线BC和B'C',的交点不一定在l上.正确的有( )A.4个 B.3个 C.2个 D.1个图15—4—6二、填空题1.已知线段AB,直线CD⊥AB于O,OA=OB,若点M在直线CD上,则MA= ;若NA=NB,则点N在 .2.△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长为12cm,AC=5cm,则△ABC的周长为 .3.如图15—4—7,A是直线MN外一点,按照下列作图语句画图并填空.图15—4—7①作点A关于直线MN的对称点A'.②在MN上任取一点B,连结AB和A'B,那么线段AB关于直线MN的对称线段是 .③在直线A、B和直线MN外任取一点C',作点C'关于直线MN的对称点C,连结AC、BC、A'C'、BC',那么△ABC与△A'B'C'关于直线MN .三、解答题1.图15—4—8中直线l是对称轴,画出图形关于l对称的另一半,想像一下整个图形的形状. (1) (2) (3) (4) (5) (6) 图15—4—8
提升小结 通过本节课的学习你有什么收获?把你的收获与全班同学分享。你还有什么问题吗?教师点评各小组的学习表现。
课后反思
课题 10.2.1 图形的平移
导学目标 1、通过具体实例认识图形的平移;2、会找对应点、对应线段和对应角;3、能按要求作出简单的平面图形平移后的图形.
重难点 1.理解平移是由移动方向和距离所决定。 2. 找到图形平移的方向和距离。
自学导航 (学生自学课本112-113页内容思考回答下面的问题:)1、 ,简称为平移。它是由移动的 和 所决定。2、有些平面图形可以看成是某一 的平面图形沿着一定的方向移动而产生的。3、请同学们尽可能多的说出现实生活中平移的例子。4、如右图,把△ABC沿着直尺PQ平移到△A/B/C/。请回答:点A、B、C的对应点分别是 、 、 ;线段AB、BC、AC的对应线段分别是 、 、 ;∠A、∠B、∠C的对应角分别是 、 、 。
合作交流展示 如下图,△ABC沿着由点A到点A/的方向,平移到△A/B/C/的位置。请在图上标出点M、N的对应点M′、N′的位置。
自学检测 1、平移改变的是图形的( ) A、位置 B、大小 C、形状 D、位置、大小和形状2、经过平移,图形上每个点都沿同一方向移动了一段距离,下列说法正确的是( )A、不同的点移动的距离不同; B、既可能相同也可能不同;C、不同的点移动的距离相同; D、无法确定3、如下图,△ABC和△DEF都是等边三角形,其中一个等边三角形经过平移后成为另一个等边三角形。(1)指出点A、B、C的对应点;(2)指出线段AB、BC、AC的对应线段;(3)指出∠A、∠B、∠C的对应角。如图,小船经过平移到了新的位置,请把缺少的图形补上。
总结提升 1、对图形的平移的定义的理解; 2、决定平移的两个因素;3、如右图,在长方形ABCD中,对角线AC与BD相交于点O,画出△A0B平移后的三角形,其中平移的方向为射线AD的方向,平移的距离为线段AD的长。
课后反思
课题 10.2.2 平移的特征
目标 探究平移的基本性质; 2、理解对应点连线平行且相等的性质;3、能按要求作出平面图形平移后的图形.
重难点 1.平移的特征和平移的基本性质 2.理解平移的特征和平移的基本性质
自学导航 (认真阅读课本114-116页例题完,思考回答下面的问题):1、平移后的图形与原来的图形的 平行且相等, 相等;平移只改变图形的 ,图形的 和 都没有发生变化。2、平移后对应点所连的线段 。3、注意:在平移过程中, 也可能在一条直线上, 也可能在一条直线上。4、如右图,△ABC经过平移到△A′B′C′的位置。(1)请写出图中所有平行、相等的线段和相等的角;(2)指出平移的方向,并量出平移的距离。
合作交流展示 如下图方格纸中,(1)、画出将图中的△ABC向右平移5格后的△A′B′C′;(2)、画出将△A′B′C′向上平移2格后的△A′′B′′C′′;(3)、△A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
自学检测 1、如下图,可经平移由一个图形得到另一个图形的是 ( )2、如图,△ABC经过平移后成为△A′B′C′,画出平移的方向、量出平移的距离.3、如右图,将所给图形沿着PQ方向平移距离为线段PQ的长。画出平移后的新图形
总结提升 1、回忆本节课学习的图形的平移的基本性质;2、如图,在纸上画△ABC和两条平行的对称轴m、n.画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″.观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗
课后反 思
第一课时10.3图形的旋转(1)
课 题 10.3 图形的旋转(1) 课 型 第一课时
策划者 审核者 导学者
学习时间 学习者 班 级
学习目标 1.了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及其应用它们解决一些实际问题.2.让学生感受生活中的几何,通过不同的情景设计归纳出图形旋转的有关概念,并用这些概念来解决一些问题
学习重点 旋转及对应点的有关概念及其应用
学习难点 从活生生的数学中抽出概念
教学准备 小黑板 三角尺
激趣明标 1.将如图所示的四边形ABCD平移,使点B的对应点为点D,作出平移后的图形.2.如图,已知△ABC和直线L,请你画出△ABC关于L的对称图形△A′B′C′. 3.圆是轴对称图形吗?等腰三角形呢?你还能指出其它的吗? (1)平移的有关概念及性质. (2)如何画一个图形关于一条直线(对称轴)的对称图形并口述它既有的一些性质. (3)什么叫轴对称图形?
自主学习 自学教材118页内容并思考:1、你能举出生活中与旋转现象有关的例子吗?2、它们是怎样旋转的,你能类比平移的定义概况出旋转的定义吗?自学检测:1、在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________.2、△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置. (1)旋转中心是哪一点 旋转了多少度 (2)如果M是AB的中点,那么经过上述旋转后,点M旋转到了什么位置
合作展示 1.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中: (1)旋转中心是什么?旋转角是什么?(2)经过旋转,点A、B分别移动到什么位置? 2.(学生活动)如图,四边形ABCD、四边形EFGH都是边长为1的正方形. (1)这个图案可以看做是哪个“基本图案”通过旋转得到的? (2)请画出旋转中心和旋转角.(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
当堂测试 一、选择题1.在26个英文大写字母中,通过旋转180°后能与原字母重合的有( ). A.6个 B.7个 C.8个 D.9个2.从5点15分到5点20分,分针旋转的度数为( ). A.20° B.26° C.30° D.36°3.如图1,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ).A.70° B.80° C.60° D.50° (1) (2) (3) 二、填空题.1.如图2,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是_____.2.如图3,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是____;(2)旋转角度是____;(3)△ADP是______三角形.三、综合提高题.1.阅读下面材料:如图4,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.如图5,以BC为轴把△ABC翻折180°,可以变到△DBC的位置. (4) (5) (6) 如图6,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换. 回答下列问题 如图7,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB. (1)在如图7所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?(2)指出如图7所示中的线段BE与DF之间的关系.2.一块等边三角形木块,边长为1,如图,现将木块沿水平线翻滚五个三角形,那么B点从开始至结束所走过的路径长是多少? ( http: / / www. )
提升小结 旋转的概念:在平面内将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.平移与旋转的异同。
课后反思
第2课时图形的旋转
课题 图形的旋转 课型 第二课时
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用. 2.通过师生互动、合作交流以及动手操作过程,发现旋转变换所蕴含的美,激发学习数学的兴趣。
学习重点 图形的旋转的基本性质及其应用。
学习难点 运用操作实验几何得出图形的旋转的三条基本性质.
教学准备
激趣明标 1.什么叫旋转?什么叫旋转中心?什么叫旋转角? 2.什么叫旋转的对应点? 3.请独立完成下面的题目.如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形? (老师点评)分析:能.看做是一条边(如线段AB)绕O点,按照同一方法连续旋转60°、120°、180°、240°、300°形成的.
自主学习 上面的解题过程中,能否得出什么结论,请回答下面的问题: 1.A、B、C、D、E、F到O点的距离是否相等? 2.对应点与旋转中心所连线段的夹角∠BOC、∠COD、∠DOE、∠EOF、∠FOA是否相等? 3.旋转前、后的图形这里指三角形△OAB、△OBC、△OCD、△ODE、△OEF、△OFA全等吗? 老师点评:(1)距离相等,(2)夹角相等,(3)前后图形全等,那么这个是否有一般性?下面请看这个实验. 请看我手里拿着的硬纸板,我在硬纸板上挖下一个三角形的洞,再挖一个点O作为旋转中心,把挖好的硬纸板放在黑板上,先在黑板上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心O转动硬纸板,在黑板上再描出这个挖掉的三角形(△A′B′C′),移去硬纸板.(分组讨论)根据图回答下面问题(一组推荐一人上台说明) 1.线段OA与OA′,OB与OB′,OC与OC′有什么关系? 2.∠AOA′,∠BOB′,∠COC′有什么关系? 3.△ABC与△A′B′C′形状和大小有什么关系?
合作展示 1.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形. 2.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形. (1)旋转中心是哪一点? (2)旋转了多少度? (3)AF的长度是多少?(4)如果连结EF,那么△AEF是怎样的三角形? 3.如图,已知正方形ABCD的对角线交于O点,若点E在AC的延长线上,AG⊥EB,交EB的延长线于点G,AG的延长线交DB的延长线于点F,则△OAF与△OBE重合吗?如果重合给予证明,如果不重合请说明理由?
当堂测试 一、选择题1.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于( ) A.50° B.210° C.50°或210° D.130°2.在图形旋转中,下列说法错误的是( ) A.在图形上的每一点到旋转中心的距离相等 B.图形上每一点移动的角度相同 C.图形上可能存在不动的点 D.图形上任意两点的连线与其对应两点的连线长度相等3.如图,下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )二、填空题1.在作旋转图形中,各对应点与旋转中心的距离________.2.如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是________,它们之间的关系是______,其中BD=_________.3.如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是________.三、综合提高题1.如图,正方形ABCD的中心为O,M为边上任意一点,过OM随意连一条曲线,将所画的曲线绕O点按同一方向连续旋转3次,每次旋转角度都是90°,这四个部分之间有何关系?2.如图,以△ABC的三顶点为圆心,半径为1,作两两不相交的扇形,则图中三个扇形面积之和是多少?
提升小结 旋转的性质:1、旋转不改变图形的大小和形状。 2、任意一对对应点与旋转中心的连线所成的角 都是旋转角,旋转角都相等。 3、对应点到旋转中心的距离相等。
课题 10.4 中心对称 课型(课时) 新授(第1课时)
策划者 审核者 导学者
学习时间 学习者 班级 九年级
学习目标 1.通过旋转作图认识两个图形关于某一点对称(或中心对称)的本质;就是一个图形绕一点旋转180°而成。2.通过作图探索中心对称的两个图形的性质;会利用中心对称的性质作出某一图形成中心对称的图形;会确定对称中心的位置。3.经历对日常生活中与中心对称有关的图形进行观察、分析、欣赏、动手操作、画图等过程,感受生活中的对称美。
学习重点 中心对称的性质及应用。
学习难点 确定对称中心的位置。
教学准备
激趣明标 问题:作出如图的两个图形绕点O旋转180°的图案,并回答下列的问题: 1.以O为旋转中心,旋转180°后两个图形是否重合?2.各对称点绕O旋转180°后,这三点是否在一条直线上? ( http: / / www. )
自主学习 如图所示的两个图案绕O旋转180°都是重合的,即甲图与乙图重合,△OAB与△COD重合. 像这样,把一个图形绕着某一个点旋转180°,如果它能够与另一个图形 ,那么就说这两个图形关于这个点对称或中心对称,这个点叫做 . 这两个图形中的对应点叫做关于中心的对称点. 例1.如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答. (1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.分析:(1)根据中心对称的定义便直接可知这两个图形是中心对称图形,对称中心就是旋转中心.(3)旋转后的对应点,便是中心的对称点.归纳:1.中心对称的两个图形,对称点所连线段都经过 ,而且被 所平分. 2.关于中心对称的两个图形是 图形例2.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称. 分析:中心对称就是旋转180°,关于点O成中心对称就是绕O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到。
合作展示 例3.如衅,在△ABC中,∠C=70°,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置. (1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积.(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,写出y与x的关系式. 分析:(1)∵BC=4,AC=4 ∴△ABC是等腰直角三角形,易得△BDC′也是等腰直角三角形且BC′=1 (2)∵平移的距离为x,∴BC′=4-x学生自主学习,完成例题的学习。请各个小组上台演示解答过程。
当堂测试 一、选择题 1.在英文字母VWXYZ中,是中心对称的英文字母的个数有( )个. A.1 B.2 C.3 D.42.下面的图案中,是中心对称图形的个数有( )个 A.1 B.2 C.3 D.43.如图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,则∠1=( )A.55° B.125° C.70° D.110°二、填空题 1.关于某一点成中心对称的两个图形,对称点连线必通过_________. 2.把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形是_________图形. 3.用两个全等的直角非等腰三角形可以拼成下面图形中的哪几种:_______(填序号) (1)长方形;(2)菱形;(3)正方形;(4)一般的平行四边形;(5)等腰三角形;(6)梯形.三、综合提高题 1.仔细观察所列的26个英文字母,将相应的字母填入下表中适当的空格内.A B C D E F G H I J K L M N O P Q R S T U V W X Y Z对称形式 轴对称旋转对称中心对称只有一条对称轴有两条对称轴2.如图,在正方形ABCD中,作出关于P点的中心对称图形,并写出作法. 3.如图,是由两个半圆组成的图形,已知点B是AC的中点,画出此图形关于点B成中心对称的图形. 4. 如衅,在△ABC中,∠C=70°,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置. (1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积.(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,写出y与x的关系式.
提升小结 谈谈自己对这节课的感受,教师点评各个小组的表现。
课后反思
第2课时10.4中心对称图形
课题 10.4中心对称图形 课型(课时) 新授(第2课时)
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.经历观察图形的过程,建立中心对称图形的概念,会判断一个图形是不是中心对称图形。2.通过动手操作,总结找中心对称图形对称中心的方法,发展归纳、总结的能力,积累问题的能力。
学习重点 中心对称图形的概念及其他运用
学习难点 中心对称图形性质的灵活运用
教学准备
激趣明标 本节课我们来学习一种具有特殊性质的图形,它们是一个图形经过旋转180°后旋转形成的图形,到底它们是怎样的呢?让我们一起来认识吧!
自主学习 1.作图题.(1)作出线段AO关于O点的对称图形,如图所示.(2)作出三角形AOB关于O点的对称图形,如图所示.(1)题就是将线段AB绕它的中点旋转180°,因为OA=OB,所以,就是线段AB绕它的中点旋转180°后与它重合.上面的(2)题,连结AD、BC,则刚才的两个关于中心对称的两个图形,就成平行四边形,如图所示. ∵AO=OC,BO=OD,∠AOB=∠COD ∴△AOB≌△COD ∴AB=CD 也就是,ABCD绕它的两条对角线交点O旋转180°后与它本身重合.因此,像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形 ,那么这个图形叫做 ,这个点就是它的对称中心2.举出学过的哪些几何图形是中心对称图形3.课前准备一些精美的中心对称图形,用图片给予展示。
合作展示 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长. 分析:将矩形折叠,使C点和A点重合,折痕为EF,就是A、C两点关于O点对称,这方面的知识在解决一些翻折问题中起关键作用,对称点连线被对称轴垂直平分,进而转化为中垂线性质和勾股定理的应用,求线段长度或面积.学生通过自主学习,共同展示各个小组对以上内容的学习。教师给予适当的鼓励和点评。
当堂测试 一、选择题 1.下列图形中,既是轴对称图形,又是中心对称图形的是( ) A.等边三角形 B.等腰梯形 C.平行四边形 D.正六边形 2.下列图形中,是中心对称图形,但不是轴对称图形的是( ). A.正方形 B.矩形 C.菱形 D.平行四边形 3.如图所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是( )A.21085 B.28015 C.58012 D.51082二、填空题 1.把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做__________. 2.请你写出你所熟悉的三个中心对称图形_________. 3.中心对称图形具有什么特点(至少写出两个)_____________.三、解答题 1.在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角,例如:正方形绕着它的对角线的交点旋转90°后能与自身重合,所以正方形是旋转对称图形,应有一个旋转角为90°. (1)判断下列命题的真假(在相应括号内填上“真”或“假”) ①等腰梯形是旋转对称图形,它有一个旋转角为180°;( ) ②矩形是旋转对称图形,它有一个旋转角为180°;( ) (2)填空:下列图形中是旋转对称图形,且有一个旋转角为120°是_____.(写出所有正确结论的序号) ①正三角形;②正方形;③正六边形;④正八边形.(3)写出两个多边形,它们都是旋转对称图形,却有一个旋转角为72°,并且分别满足下列条件:①是轴对称图形,但不是中心对称图形;②既是轴对称图形,又是中心对称图形. 2.如图,将矩形A1B1C1D1沿EF折叠,使B1点落在A1D1边上的B处;沿BG折叠,使D1点落在D处且BD过F点. (1)求证:四边形BEFG是平行四边形;(2)连接BB,判断△B1BG的形状,并写出判断过程.
提升小结 通过本节课的学习你有什么收获?把你的收获与全班同学分享。你还有什么问题吗?教师点评各小组的学习表现。
课后反思
课题 10.5 图形的全等
目标 1、了解全等图形、全等多边形、全等三角形。2、掌握全等多边形性质与识别方法,全等三角形的性质。?3、简单应用全等多边形性质、全等三角形的性质解决实际问题。
重难点 1、全等多边形的性质与识别方法;2、全等三角形的性质应用。
教学环节 生生互动
复习回顾承上启下 三角形的概念。三角形中三条重要的线段—角平分线、中线、高线。
讨论新知尝试发现 1、观察教材P92的两组图形,说一说他们有什么共同的特征? 能够完全重合的两个图形称为 。2、列举生活中全等图形的实例。3、探索全等三角形。(1)能够完全重合的两个三角形叫做 记作 (2)全等三角形的 相等, 相等。(3)全等三角形对应边的高相等吗?对应边的中线呢?还有那些线段相等?
归纳总结巩固提升 观察下面三组图形,它们是不是全等图形?为什么?2、如图:△AOD≌△BOC,写出其中相等的角。
拓展应用发现新知 1、如图:△ABC≌△AEC, ∠B=30°, ∠ACB=85°,求出△AEC各内角的度数。如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°, 则BC=_____cm,∠B=_____。你还能求出哪些边的长度,哪些角的度数
课堂小结
课后反思
(A)
(B)
(C)
(D)
L
A
B
C
D
L
L
B
A
A
B
A
B
C
E
D
B
A
A
B
A
B
C
E
D
A
B
A′
C
B′
C′
A
B
C
D
A
B
A
B
C
E
D
A
B
A
B
C
E
D
A
D
B
C
O
A
D
C
B
O
A
E
C
B
F
课 题 10.1.1 生活中的轴对称 课 型 第一课时
策划者 审核者 导学者
学习时间 学习者 班 级
学习目标 (1)通过生活中的轴对称现象,了解轴对称图形及轴对称的区别与联系;(2)加深这两个概念的理解,能正确识别轴对称图形,培养观察能力;(3)体会轴对称在现实生活中的广泛运用和它的美学价值;
学习重点 轴对称图形的概念.
学习难点 判断图形是否是轴对称图形
教学准备 三角尺
激趣明标 1.观察一下书P98中的图形,它们都是 ( )图形,这些图形有什么特点呢?(让学生说一说) 2、轴对称图形的定义: 如果一个图形沿某条直线对折,对折两部分( ),那么这个图形 ( ),这条直线叫做这个图形的 ( )。3、画出书中图10.1.1中各图形的对称轴。是不是每一个轴对称图形都只有一条对称轴?答: 。
自主学习 自学教材99-100页轴对称的定义:把一个图形沿着某一条直线翻折过去,如果它能够与( )重合,那么就说这两个图形( ),这条直线就是( ) ,两个图形中的对应点(即两个图形重合时互相重合的点)叫做( )。5、轴对称图形和轴对称的区别与联系 区别:(1)轴对称图形是指一个具有特殊形状的图形,只对( )个 图形而言;轴对称是指( )个图形的位置的关系,必须涉及( )个图形。(2)轴对称图形的对称轴( );轴对称只有 ( )。 联系:(1)图中都有一条直线,都要沿着这条直线 。(2)如果把两个成轴对称图形拼在一起,看成一个整体,那么它就是一个 。如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成( )。 (3)轴对称图形(或关于某条直线对称的两个图形)沿对称轴对折后的两部分是 的,所以它的对应线段(对折后重合的线段)( ),对应角(对折后重合的角)( )。
合作展示 1、如图是否为轴对称图形,若是请画出对称轴。 2、观察下图中各种图形,说出哪些图形可以放在一起形成轴对称(可以将图形上下放置或左右放置)解:左右放置可以形成轴对称的有:(1)和( ),(2)和( ),(9)和( ); 上下放置可以形成轴对称的有:(2)和( ),(5 和( ),(7)和( )。3、下图中的各图形共同特点是什么?你觉得图中哪一个图形比较独特,简单说明你的理由。解:它们的共同特点是都是 。这五个图形中,图 都是有两条对称轴,只有图 有无数条对称轴,所以这样看来图 比较独特。
当堂测试 1.如图所示的标志中,是轴对称图形的有( ) A.1个 B.2个 C.3个 D.4个2.如图是用纸折叠成的图案,其中是轴对称图形的有( )A.1个 B.2个 C.3个 D.4个3.正五角星的对称轴的条数是( )A.1条 B.2条 C.5条 D.10条4.下列图形中有4条对称轴的是( )A.平行四边形 B.矩形 C.正方形 D.菱形5.下列平面图形中,不是轴对称图形的是 ( ) B)6.下列英文字母属于轴对称图形的是 ( )(A) N (B) S (C) H (D) K7.仔细观察下列图案,并按规律在横线上画出合适的图形. _________ 8、一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时,它所看到的全身像是( )9、已知图中的图形都是轴对称图形,请你画出它们的对称轴.10、以“○○,△△,_ _ _”(即两个圆,两个三角形,三条线段)为条件,画出一个有实际意义的对称图形. ( http: / / www. )
提升小结 轴对称的概念:轴对称与成轴对称的区别寻找对称轴
课后反思
第2课时 轴对称的再认识
课题 轴对称的再认识 课型 第二课时
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.探索线段、角的轴对称性。2.会找图形的对称轴。
学习重点 探索线段、角的轴对称性
学习难点 找已知图形的对称轴
教学准备 三角尺
激趣明标 1.什么叫轴对称?什么叫对称轴? 2.我们上期学过的线段和角是轴对称图形吗,你能找出对称轴吗?
自主学习 一、 探索线段、角的轴对称性1.探索线段的轴对性(1)动手做一做:在纸上画出线段AB及它的中点O,再过点O画出与AB垂直的直线CD,沿直线CD将纸对折,看看线段OA与OB是否能够重合?(2)从上面的操作你可以看出线段是 图形,它的对称轴是 。2.探索角的轴对称性(1)动手做一做:在纸上画出∠AOB,对折,使角的两边完全重合,然后用直尺画出折痕OM,看看射线OM与∠AOB 是什么关系?(2)从上面的操作可以看出,角是 图形,它的对称轴是 。(注意对称轴描述时的准确性)
合作展示 找图形的对称轴(1)阅读P102--P103的内容(从第二个“试一试”开始,读完第二个“做一做”),完成课本及云图中的问题。并归纳出画复杂的轴对称图形的对称轴的步骤。(2)你还能找到其他画轴对称图形的对称轴的方法吗?(3)通过以上的操作,可以得到:如果一个图形是轴对称图形,那么 是该图形的对称轴。这也是轴对称图形的一个重要性质。
当堂测试 1.课本P104—P105练习 1、2、32.如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( )A.6 B.8 C.9 D.103.如下图,已知平面上的直线L和两点A、B,在直线L上求作一点P,使PA=PB.AB4.将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是( )
提升小结 1.强调角的对称轴是角的平分线所在的直线。2.画复杂的轴对称图形的对称轴的步骤:(1)找出轴对称图形的任意一组对称点;(2)连接这组对称点;(3)画出对称点所连线段垂直平分线,这条垂直平分线就是该图形的对称轴。3.其他方法有:找两组对称点并连接,分别取这两条线段的中点,过这两个中点所作的直线就是图形的对称轴。
课题 画轴对称图形 课型(课时) 新授(第3课时)
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.使学生能够按要求作出简单平面图形经过一次对称后的图形。 2.通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操
学习重点 让学生识别轴对称图形与画轴对称图形的对称轴。
学习难点 区别轴对称与轴对称图形两个不同的概念
教学准备 三角尺
激趣明标 叫做轴对称图形。怎样寻找对称轴
自主学习 如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢 请同学们尝试解决以下问题:如图(1),(2)实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形。 3、如图,已知点A和L直线,试画出点A关于直线l的对称点A′。 LA· 4、请你画出图中A、B、C三点关于直线l的对称点。 AB C
合作展示 1.已知△ABC,直线L,画出△ABC关于直线L的对称图形。 A B C 2、在图中分别画出点A关于两条直线的对称点和点.3、 画出所示图形关于直线的对称图形.
当堂测试 1、填空:(1)、圆有 对称轴。(2)、正方形有 条对称轴,长方形有 条对称轴,等腰三角形有 条对称轴,等边三角形有 条对称轴。2、如图,分别以AB为对称轴,画出各图形的对称图形,并观察图形(3)和它的轴对称图形构成一个 三角形.3、一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 。4、星期天小华去书店买书时,从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)的位置如图所示,此时时针表示的时间是 。5、下列图形中,是轴对称图形的是( )6、从A地到河边取水后返回B地,如何走路程最短?请作图示意。
提升小结 谈谈自己对这节课的感受,教师点评各个小组的表现。
课后反思
第4课时 设计轴对称图案
课题 设计轴对称图案 课型(课时) 新授(第4课时)
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.使学生能设计简单的轴对称图案。 2.使学生能够欣赏现实生活中的轴对称图形。
学习重点 利用对称轴进行图案设计。
学习难点 寻找对称轴以及如何利用对称轴作轴对称图形。
教学准备
激趣明标 1.如图(1),请画出△ABC的关于直线l对称的图形。 A A l B C B C 图(1) 图(2)2.如图(2),等边△ABC是轴对称图形吗 如果是,它有几条对称轴 画画试试看。
自主学习 在日常生活中,我们可以看到丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中有许多轴对称图形。请同学们欣赏P107页四个装饰图案。如图(3)是一个轴对称图形。 问:1.有多少条对称轴呢 2.可以利用轴对称性来画出它吗 请准备一张正方形纸片,按以下5个步骤一起来画。 (1)在正方形纸片上画出四条对称轴。 (2)在其中一个三角形中,如图,画出图形形状的基本线条。(注意:不同的线条最终会得到不同的图案,你可以自己设计线条,而不必和书上一样。) (3)按照其中一条斜的对称轴画出(2)中图形的对称图形。 (4)按照另一条斜的对称轴画出(3)中图形的对称图形。 (5)按照水平(或垂直)对称画出(4)中图形的对称图形,即得到图(3)中的图。 在图案上涂上你喜欢的颜色,擦掉其他的线条,轴对称的图案就完成了。
合作展示 图15—4—9中各图是只有一条对称轴的图形,请你涂黑图形的一部分,使它成为具有两条对称轴的图形.下面各图是只有一条对称轴的图形,请你涂黑图形的一部分,使它成为具有两条对称轴的图形.图15—4—9图15—4—1
当堂测试 一、选择题1.下列命题中,正确的是( )A.两个全等的三角形合在一起是一个轴对称图形B.等腰三角形的对称轴是底边上的中线C.等腰三角形底边上的高就是底边的垂直平分线D.一条线段可以看做以它的垂直平分线为轴的轴对称图形2.下列说法中,正确的是( )A.两个全等三角形,一定是轴对称的B.两个轴对称的三角形,一定是全等的C.三角形的一条中线把三角形分成以中线为轴对称的两个图形D.三角形的一条高把三角形分成以高线为轴对称的两个图形3.在直线、线段、角、两条平行直线、两条相交直线这些图形中,是轴对称图形的有( )A.5个 B.4个 C.3个 D.2个4.如图15—4—6,△ABC和△A'B'C'关于直线l对称,下列结论中:①△ABC△A'B'C';②∠BAC'=∠B'AC;③l垂直平分CC';④直线BC和B'C',的交点不一定在l上.正确的有( )A.4个 B.3个 C.2个 D.1个图15—4—6二、填空题1.已知线段AB,直线CD⊥AB于O,OA=OB,若点M在直线CD上,则MA= ;若NA=NB,则点N在 .2.△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长为12cm,AC=5cm,则△ABC的周长为 .3.如图15—4—7,A是直线MN外一点,按照下列作图语句画图并填空.图15—4—7①作点A关于直线MN的对称点A'.②在MN上任取一点B,连结AB和A'B,那么线段AB关于直线MN的对称线段是 .③在直线A、B和直线MN外任取一点C',作点C'关于直线MN的对称点C,连结AC、BC、A'C'、BC',那么△ABC与△A'B'C'关于直线MN .三、解答题1.图15—4—8中直线l是对称轴,画出图形关于l对称的另一半,想像一下整个图形的形状. (1) (2) (3) (4) (5) (6) 图15—4—8
提升小结 通过本节课的学习你有什么收获?把你的收获与全班同学分享。你还有什么问题吗?教师点评各小组的学习表现。
课后反思
课题 10.2.1 图形的平移
导学目标 1、通过具体实例认识图形的平移;2、会找对应点、对应线段和对应角;3、能按要求作出简单的平面图形平移后的图形.
重难点 1.理解平移是由移动方向和距离所决定。 2. 找到图形平移的方向和距离。
自学导航 (学生自学课本112-113页内容思考回答下面的问题:)1、 ,简称为平移。它是由移动的 和 所决定。2、有些平面图形可以看成是某一 的平面图形沿着一定的方向移动而产生的。3、请同学们尽可能多的说出现实生活中平移的例子。4、如右图,把△ABC沿着直尺PQ平移到△A/B/C/。请回答:点A、B、C的对应点分别是 、 、 ;线段AB、BC、AC的对应线段分别是 、 、 ;∠A、∠B、∠C的对应角分别是 、 、 。
合作交流展示 如下图,△ABC沿着由点A到点A/的方向,平移到△A/B/C/的位置。请在图上标出点M、N的对应点M′、N′的位置。
自学检测 1、平移改变的是图形的( ) A、位置 B、大小 C、形状 D、位置、大小和形状2、经过平移,图形上每个点都沿同一方向移动了一段距离,下列说法正确的是( )A、不同的点移动的距离不同; B、既可能相同也可能不同;C、不同的点移动的距离相同; D、无法确定3、如下图,△ABC和△DEF都是等边三角形,其中一个等边三角形经过平移后成为另一个等边三角形。(1)指出点A、B、C的对应点;(2)指出线段AB、BC、AC的对应线段;(3)指出∠A、∠B、∠C的对应角。如图,小船经过平移到了新的位置,请把缺少的图形补上。
总结提升 1、对图形的平移的定义的理解; 2、决定平移的两个因素;3、如右图,在长方形ABCD中,对角线AC与BD相交于点O,画出△A0B平移后的三角形,其中平移的方向为射线AD的方向,平移的距离为线段AD的长。
课后反思
课题 10.2.2 平移的特征
目标 探究平移的基本性质; 2、理解对应点连线平行且相等的性质;3、能按要求作出平面图形平移后的图形.
重难点 1.平移的特征和平移的基本性质 2.理解平移的特征和平移的基本性质
自学导航 (认真阅读课本114-116页例题完,思考回答下面的问题):1、平移后的图形与原来的图形的 平行且相等, 相等;平移只改变图形的 ,图形的 和 都没有发生变化。2、平移后对应点所连的线段 。3、注意:在平移过程中, 也可能在一条直线上, 也可能在一条直线上。4、如右图,△ABC经过平移到△A′B′C′的位置。(1)请写出图中所有平行、相等的线段和相等的角;(2)指出平移的方向,并量出平移的距离。
合作交流展示 如下图方格纸中,(1)、画出将图中的△ABC向右平移5格后的△A′B′C′;(2)、画出将△A′B′C′向上平移2格后的△A′′B′′C′′;(3)、△A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
自学检测 1、如下图,可经平移由一个图形得到另一个图形的是 ( )2、如图,△ABC经过平移后成为△A′B′C′,画出平移的方向、量出平移的距离.3、如右图,将所给图形沿着PQ方向平移距离为线段PQ的长。画出平移后的新图形
总结提升 1、回忆本节课学习的图形的平移的基本性质;2、如图,在纸上画△ABC和两条平行的对称轴m、n.画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″.观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗
课后反 思
第一课时10.3图形的旋转(1)
课 题 10.3 图形的旋转(1) 课 型 第一课时
策划者 审核者 导学者
学习时间 学习者 班 级
学习目标 1.了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及其应用它们解决一些实际问题.2.让学生感受生活中的几何,通过不同的情景设计归纳出图形旋转的有关概念,并用这些概念来解决一些问题
学习重点 旋转及对应点的有关概念及其应用
学习难点 从活生生的数学中抽出概念
教学准备 小黑板 三角尺
激趣明标 1.将如图所示的四边形ABCD平移,使点B的对应点为点D,作出平移后的图形.2.如图,已知△ABC和直线L,请你画出△ABC关于L的对称图形△A′B′C′. 3.圆是轴对称图形吗?等腰三角形呢?你还能指出其它的吗? (1)平移的有关概念及性质. (2)如何画一个图形关于一条直线(对称轴)的对称图形并口述它既有的一些性质. (3)什么叫轴对称图形?
自主学习 自学教材118页内容并思考:1、你能举出生活中与旋转现象有关的例子吗?2、它们是怎样旋转的,你能类比平移的定义概况出旋转的定义吗?自学检测:1、在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________.2、△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置. (1)旋转中心是哪一点 旋转了多少度 (2)如果M是AB的中点,那么经过上述旋转后,点M旋转到了什么位置
合作展示 1.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中: (1)旋转中心是什么?旋转角是什么?(2)经过旋转,点A、B分别移动到什么位置? 2.(学生活动)如图,四边形ABCD、四边形EFGH都是边长为1的正方形. (1)这个图案可以看做是哪个“基本图案”通过旋转得到的? (2)请画出旋转中心和旋转角.(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
当堂测试 一、选择题1.在26个英文大写字母中,通过旋转180°后能与原字母重合的有( ). A.6个 B.7个 C.8个 D.9个2.从5点15分到5点20分,分针旋转的度数为( ). A.20° B.26° C.30° D.36°3.如图1,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ).A.70° B.80° C.60° D.50° (1) (2) (3) 二、填空题.1.如图2,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是_____.2.如图3,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是____;(2)旋转角度是____;(3)△ADP是______三角形.三、综合提高题.1.阅读下面材料:如图4,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.如图5,以BC为轴把△ABC翻折180°,可以变到△DBC的位置. (4) (5) (6) 如图6,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换. 回答下列问题 如图7,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB. (1)在如图7所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?(2)指出如图7所示中的线段BE与DF之间的关系.2.一块等边三角形木块,边长为1,如图,现将木块沿水平线翻滚五个三角形,那么B点从开始至结束所走过的路径长是多少? ( http: / / www. )
提升小结 旋转的概念:在平面内将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.平移与旋转的异同。
课后反思
第2课时图形的旋转
课题 图形的旋转 课型 第二课时
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用. 2.通过师生互动、合作交流以及动手操作过程,发现旋转变换所蕴含的美,激发学习数学的兴趣。
学习重点 图形的旋转的基本性质及其应用。
学习难点 运用操作实验几何得出图形的旋转的三条基本性质.
教学准备
激趣明标 1.什么叫旋转?什么叫旋转中心?什么叫旋转角? 2.什么叫旋转的对应点? 3.请独立完成下面的题目.如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形? (老师点评)分析:能.看做是一条边(如线段AB)绕O点,按照同一方法连续旋转60°、120°、180°、240°、300°形成的.
自主学习 上面的解题过程中,能否得出什么结论,请回答下面的问题: 1.A、B、C、D、E、F到O点的距离是否相等? 2.对应点与旋转中心所连线段的夹角∠BOC、∠COD、∠DOE、∠EOF、∠FOA是否相等? 3.旋转前、后的图形这里指三角形△OAB、△OBC、△OCD、△ODE、△OEF、△OFA全等吗? 老师点评:(1)距离相等,(2)夹角相等,(3)前后图形全等,那么这个是否有一般性?下面请看这个实验. 请看我手里拿着的硬纸板,我在硬纸板上挖下一个三角形的洞,再挖一个点O作为旋转中心,把挖好的硬纸板放在黑板上,先在黑板上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心O转动硬纸板,在黑板上再描出这个挖掉的三角形(△A′B′C′),移去硬纸板.(分组讨论)根据图回答下面问题(一组推荐一人上台说明) 1.线段OA与OA′,OB与OB′,OC与OC′有什么关系? 2.∠AOA′,∠BOB′,∠COC′有什么关系? 3.△ABC与△A′B′C′形状和大小有什么关系?
合作展示 1.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形. 2.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形. (1)旋转中心是哪一点? (2)旋转了多少度? (3)AF的长度是多少?(4)如果连结EF,那么△AEF是怎样的三角形? 3.如图,已知正方形ABCD的对角线交于O点,若点E在AC的延长线上,AG⊥EB,交EB的延长线于点G,AG的延长线交DB的延长线于点F,则△OAF与△OBE重合吗?如果重合给予证明,如果不重合请说明理由?
当堂测试 一、选择题1.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于( ) A.50° B.210° C.50°或210° D.130°2.在图形旋转中,下列说法错误的是( ) A.在图形上的每一点到旋转中心的距离相等 B.图形上每一点移动的角度相同 C.图形上可能存在不动的点 D.图形上任意两点的连线与其对应两点的连线长度相等3.如图,下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )二、填空题1.在作旋转图形中,各对应点与旋转中心的距离________.2.如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是________,它们之间的关系是______,其中BD=_________.3.如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是________.三、综合提高题1.如图,正方形ABCD的中心为O,M为边上任意一点,过OM随意连一条曲线,将所画的曲线绕O点按同一方向连续旋转3次,每次旋转角度都是90°,这四个部分之间有何关系?2.如图,以△ABC的三顶点为圆心,半径为1,作两两不相交的扇形,则图中三个扇形面积之和是多少?
提升小结 旋转的性质:1、旋转不改变图形的大小和形状。 2、任意一对对应点与旋转中心的连线所成的角 都是旋转角,旋转角都相等。 3、对应点到旋转中心的距离相等。
课题 10.4 中心对称 课型(课时) 新授(第1课时)
策划者 审核者 导学者
学习时间 学习者 班级 九年级
学习目标 1.通过旋转作图认识两个图形关于某一点对称(或中心对称)的本质;就是一个图形绕一点旋转180°而成。2.通过作图探索中心对称的两个图形的性质;会利用中心对称的性质作出某一图形成中心对称的图形;会确定对称中心的位置。3.经历对日常生活中与中心对称有关的图形进行观察、分析、欣赏、动手操作、画图等过程,感受生活中的对称美。
学习重点 中心对称的性质及应用。
学习难点 确定对称中心的位置。
教学准备
激趣明标 问题:作出如图的两个图形绕点O旋转180°的图案,并回答下列的问题: 1.以O为旋转中心,旋转180°后两个图形是否重合?2.各对称点绕O旋转180°后,这三点是否在一条直线上? ( http: / / www. )
自主学习 如图所示的两个图案绕O旋转180°都是重合的,即甲图与乙图重合,△OAB与△COD重合. 像这样,把一个图形绕着某一个点旋转180°,如果它能够与另一个图形 ,那么就说这两个图形关于这个点对称或中心对称,这个点叫做 . 这两个图形中的对应点叫做关于中心的对称点. 例1.如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答. (1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.分析:(1)根据中心对称的定义便直接可知这两个图形是中心对称图形,对称中心就是旋转中心.(3)旋转后的对应点,便是中心的对称点.归纳:1.中心对称的两个图形,对称点所连线段都经过 ,而且被 所平分. 2.关于中心对称的两个图形是 图形例2.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称. 分析:中心对称就是旋转180°,关于点O成中心对称就是绕O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到。
合作展示 例3.如衅,在△ABC中,∠C=70°,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置. (1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积.(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,写出y与x的关系式. 分析:(1)∵BC=4,AC=4 ∴△ABC是等腰直角三角形,易得△BDC′也是等腰直角三角形且BC′=1 (2)∵平移的距离为x,∴BC′=4-x学生自主学习,完成例题的学习。请各个小组上台演示解答过程。
当堂测试 一、选择题 1.在英文字母VWXYZ中,是中心对称的英文字母的个数有( )个. A.1 B.2 C.3 D.42.下面的图案中,是中心对称图形的个数有( )个 A.1 B.2 C.3 D.43.如图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,则∠1=( )A.55° B.125° C.70° D.110°二、填空题 1.关于某一点成中心对称的两个图形,对称点连线必通过_________. 2.把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形是_________图形. 3.用两个全等的直角非等腰三角形可以拼成下面图形中的哪几种:_______(填序号) (1)长方形;(2)菱形;(3)正方形;(4)一般的平行四边形;(5)等腰三角形;(6)梯形.三、综合提高题 1.仔细观察所列的26个英文字母,将相应的字母填入下表中适当的空格内.A B C D E F G H I J K L M N O P Q R S T U V W X Y Z对称形式 轴对称旋转对称中心对称只有一条对称轴有两条对称轴2.如图,在正方形ABCD中,作出关于P点的中心对称图形,并写出作法. 3.如图,是由两个半圆组成的图形,已知点B是AC的中点,画出此图形关于点B成中心对称的图形. 4. 如衅,在△ABC中,∠C=70°,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置. (1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积.(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,写出y与x的关系式.
提升小结 谈谈自己对这节课的感受,教师点评各个小组的表现。
课后反思
第2课时10.4中心对称图形
课题 10.4中心对称图形 课型(课时) 新授(第2课时)
策划者 审核者 导学者
学习时间 学习者 班级
学习目标 1.经历观察图形的过程,建立中心对称图形的概念,会判断一个图形是不是中心对称图形。2.通过动手操作,总结找中心对称图形对称中心的方法,发展归纳、总结的能力,积累问题的能力。
学习重点 中心对称图形的概念及其他运用
学习难点 中心对称图形性质的灵活运用
教学准备
激趣明标 本节课我们来学习一种具有特殊性质的图形,它们是一个图形经过旋转180°后旋转形成的图形,到底它们是怎样的呢?让我们一起来认识吧!
自主学习 1.作图题.(1)作出线段AO关于O点的对称图形,如图所示.(2)作出三角形AOB关于O点的对称图形,如图所示.(1)题就是将线段AB绕它的中点旋转180°,因为OA=OB,所以,就是线段AB绕它的中点旋转180°后与它重合.上面的(2)题,连结AD、BC,则刚才的两个关于中心对称的两个图形,就成平行四边形,如图所示. ∵AO=OC,BO=OD,∠AOB=∠COD ∴△AOB≌△COD ∴AB=CD 也就是,ABCD绕它的两条对角线交点O旋转180°后与它本身重合.因此,像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形 ,那么这个图形叫做 ,这个点就是它的对称中心2.举出学过的哪些几何图形是中心对称图形3.课前准备一些精美的中心对称图形,用图片给予展示。
合作展示 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长. 分析:将矩形折叠,使C点和A点重合,折痕为EF,就是A、C两点关于O点对称,这方面的知识在解决一些翻折问题中起关键作用,对称点连线被对称轴垂直平分,进而转化为中垂线性质和勾股定理的应用,求线段长度或面积.学生通过自主学习,共同展示各个小组对以上内容的学习。教师给予适当的鼓励和点评。
当堂测试 一、选择题 1.下列图形中,既是轴对称图形,又是中心对称图形的是( ) A.等边三角形 B.等腰梯形 C.平行四边形 D.正六边形 2.下列图形中,是中心对称图形,但不是轴对称图形的是( ). A.正方形 B.矩形 C.菱形 D.平行四边形 3.如图所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是( )A.21085 B.28015 C.58012 D.51082二、填空题 1.把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做__________. 2.请你写出你所熟悉的三个中心对称图形_________. 3.中心对称图形具有什么特点(至少写出两个)_____________.三、解答题 1.在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角,例如:正方形绕着它的对角线的交点旋转90°后能与自身重合,所以正方形是旋转对称图形,应有一个旋转角为90°. (1)判断下列命题的真假(在相应括号内填上“真”或“假”) ①等腰梯形是旋转对称图形,它有一个旋转角为180°;( ) ②矩形是旋转对称图形,它有一个旋转角为180°;( ) (2)填空:下列图形中是旋转对称图形,且有一个旋转角为120°是_____.(写出所有正确结论的序号) ①正三角形;②正方形;③正六边形;④正八边形.(3)写出两个多边形,它们都是旋转对称图形,却有一个旋转角为72°,并且分别满足下列条件:①是轴对称图形,但不是中心对称图形;②既是轴对称图形,又是中心对称图形. 2.如图,将矩形A1B1C1D1沿EF折叠,使B1点落在A1D1边上的B处;沿BG折叠,使D1点落在D处且BD过F点. (1)求证:四边形BEFG是平行四边形;(2)连接BB,判断△B1BG的形状,并写出判断过程.
提升小结 通过本节课的学习你有什么收获?把你的收获与全班同学分享。你还有什么问题吗?教师点评各小组的学习表现。
课后反思
课题 10.5 图形的全等
目标 1、了解全等图形、全等多边形、全等三角形。2、掌握全等多边形性质与识别方法,全等三角形的性质。?3、简单应用全等多边形性质、全等三角形的性质解决实际问题。
重难点 1、全等多边形的性质与识别方法;2、全等三角形的性质应用。
教学环节 生生互动
复习回顾承上启下 三角形的概念。三角形中三条重要的线段—角平分线、中线、高线。
讨论新知尝试发现 1、观察教材P92的两组图形,说一说他们有什么共同的特征? 能够完全重合的两个图形称为 。2、列举生活中全等图形的实例。3、探索全等三角形。(1)能够完全重合的两个三角形叫做 记作 (2)全等三角形的 相等, 相等。(3)全等三角形对应边的高相等吗?对应边的中线呢?还有那些线段相等?
归纳总结巩固提升 观察下面三组图形,它们是不是全等图形?为什么?2、如图:△AOD≌△BOC,写出其中相等的角。
拓展应用发现新知 1、如图:△ABC≌△AEC, ∠B=30°, ∠ACB=85°,求出△AEC各内角的度数。如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°, 则BC=_____cm,∠B=_____。你还能求出哪些边的长度,哪些角的度数
课堂小结
课后反思
(A)
(B)
(C)
(D)
L
A
B
C
D
L
L
B
A
A
B
A
B
C
E
D
B
A
A
B
A
B
C
E
D
A
B
A′
C
B′
C′
A
B
C
D
A
B
A
B
C
E
D
A
B
A
B
C
E
D
A
D
B
C
O
A
D
C
B
O
A
E
C
B
F
