第6章 一元一次方程 素养基础卷(含解析)
文档属性
| 名称 | 第6章 一元一次方程 素养基础卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 721.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 13:43:08 | ||
图片预览




文档简介
第6章 一元一次方程 素养基础卷
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.下列是一元一次方程的是( )
A. B. C. D.
2.已知,根据等式的基本性质,下列变形错误的是( )
A. B. C. D.
3.如果的值与的值相等,那么x的值为( )
A.9 B. C.3 D.
4.佳佳同学解一元一次方程的过程如下:
解:去分母,得,第一步
去括号,得,第二步
移项,得,第三步
合并同类项,得,第四步
系数化为1,得.
前四个步骤中,开始出现错误的是( )
A.第一步 B.第二步 C.第三步 D.第四步
5.小刚同学在做作业时,不小心将方程中的一个常数涂黑了,在询问老师后,老师告诉她方程的解是请问这个被涂黑的常数是( )
A. B.4 C. D.2
6.若关于x的方程的解为正整数,则整数k的值为( )
A.1 B.2 C.3或4 D.0或1
7.《九章算术》成书于公元1世纪,是古代中国乃至东方的第一部自成体系的数学专著,《九章算术》的算法体系至今仍在推动着计算机的发展和应用.书中记载了这样一题:“今有程传委输(驿站受托运粮),空车日行七十里,重车日行五十里.今载太仓粟输上林,五日三返(五天往返三趟).问太仓去(距离)上林几何(多远)?”用现在的解法,设太仓到上林的距离为x里,可列方程( )
A. B. C. D.
8.规定新运算“*”:对于任意实数都有,例如:,若,则的值为( )
A. B. C. D.1
9.已知一个小长方形的长和宽分别是和2,当5个形状、大小相同的小长方形拼成一个如图所示的大长方形,所标尺寸如图所示,求图中阴影部分面积是( )
A.18 B.27 C.29 D.33
10.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图),将个数填在的方格中,如果满足每行、每列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则的值为( )
A. B. C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如果,那么成立时c应满足的条件是 .
12.请你帮助乐乐同学写一个满足下列条件的一元一次方程:①含未知数项的系数为负数;②方程左边只有两项且右边等于零;③方程的解为.你写的方程是 .
13.已知关于的方程的解是,则的值为 .
14.在手工制作课上,老师组织七年级一班的学生用硬纸制作圆柱形茶叶筒.七年级一班共有学生人,每名学生每小时剪筒身个或剪筒底个.要求一个筒身配两个筒底,那么安排 人剪筒身,才能使每小时剪出的筒身与筒底配套.
15.电影《哈利·波特》中,哈利·波特穿墙进入“站台”的镜头(如图中的A站台),构思巧妙,给观众留下了深刻的印象.若B,C分别称为“站台”和“站台”,且,则D站台用类似电影中的方法可称为“ 站台”.
三、解答题
16.解方程:
(1);(2).
17.小明在学习了等式的基本性质后,对等式进行变形,得出“”的错误结论,但他找不到错误原因,聪明的你能帮助他找到原因吗?小明的具体过程如表所示:
将等式变形 两边同时加,得(第①步) 两边同时除以,得(第②步)
(1)第______步等式变形产生错误;
(2)请分析产生错误的原因,写出等式正确变形过程,求出的值.
18.如图是两张不同类型火车的车票:(“次”表示动车,“次”表示高铁).已知该动车和高铁的平均速度分别为,,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离.
19.已知关于的方程与有相同的解.
(1)求的值;
(2)求关于的方程的解.
20.在劳动课上,老师组织七年级(1)班的学生自己动手整理操场.七年级(1)班共有学生48人,其中女生人数比男生人数的多3人.如果让男生单独工作,需要5小时,如果让女生单独工作,需要小时.
(1)七年级(1)班有男生、女生各多少人?
(2)如果让男生、女生一起工作1小时,再由男生单独完成剩余的部分,求男生共需要多少时间?
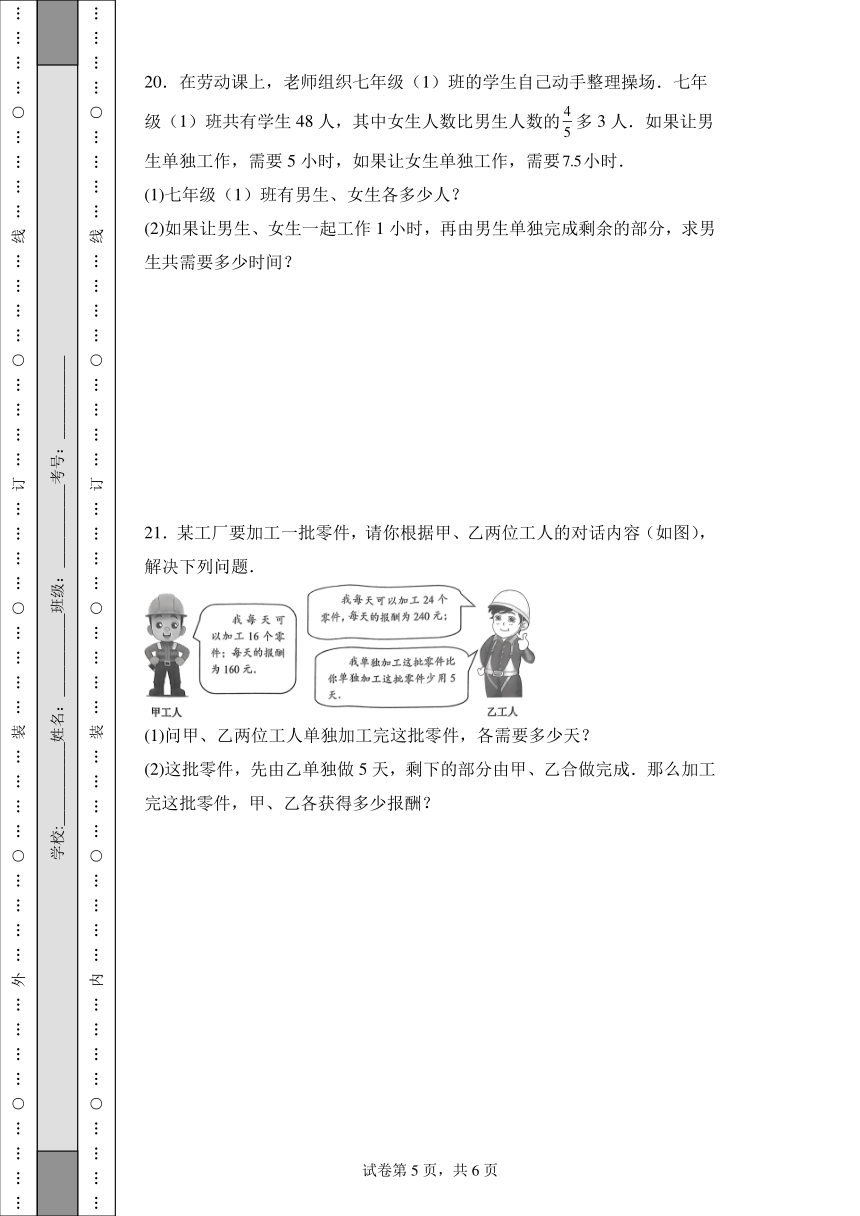
21.某工厂要加工一批零件,请你根据甲、乙两位工人的对话内容(如图),解决下列问题.
(1)问甲、乙两位工人单独加工完这批零件,各需要多少天?
(2)这批零件,先由乙单独做5天,剩下的部分由甲、乙合做完成.那么加工完这批零件,甲、乙各获得多少报酬?
22.定义:如果两个一元一次方程的解互为相反数,我们就称这两个方程为“和谐方程”.
例如:方程和为“和谐方程”.
(1)若关于的方程与方程是“和谐方程”,求的值;
(2)若“和谐方程”的两个解的差为4,其中一个解为,求的值;
(3)若无论取任何有理数,关于的方程(,为常数)与关于的方程都是“和谐方程”,求与的值.
23.一种商品按销售量分三部分制定销售单价,如下表:
销售量 单价
不超过100件部分 2.6元/件
超过100件不超过300件部分 2.2元/件
超过300件部分 2元/件
(1)若买100件花______元,买260件花______元;买350件花______元;
(2)某社团为举行活动花了568元买这种商品作为纪念品,求购买这种商品多少件?
(3)若张强花了元,恰好购买件这种商品,求的值.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校
:___________
姓名:
___________
班级:
___________
考号:
___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.A
【分析】本题主要考查了一元一次方程的定义,一元一次方程的定义:只含有一个未知数,且未知数的次数是1,且两边都是整式,这样的方程叫一元一次方程.根据一元一次方程的定义一一判断即可.
【详解】解:A.只含有一个未知数,未知数的次数是1,且两边都是整式,是一元一次方程,故本选项符合题意;
B.分母中含有未知数,不是整式,不是一元一次方程,故本选项不符合题意;
A.只含有一个未知数,但不是等式,不是一元一次方程,故本选项不符合题意;
D.含有两个未知数,不是一元一次方程,故本选项不符合题意;
故选:A.
2.C
【分析】此题主要考查了等式的基本性质,等式的性质1、等式两边加同一个数(或式子)结果仍得等式;2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.根据等式的基本性质,对题目中的四个选项逐一进行判断即可得出答案.
【详解】解:将等式的两边同时加上1,得:,
故选项A正确,不符合题意;
将等式的两边同时减去1,得:,
故选项B正确,不符合题意;
将等式的两边同时乘以,得:,
故选项C不正确,符合题意;
将等式的两边同时除以2,得:,
故选项D正确,不符合题意.
故选:C.
3.A
【分析】此题考查了解一元一次方程,熟练掌握解法是解本题的关键.利用的值与的值相等,列出方程,求出方程的解即可得到x的值.
【详解】解:根据题意得:,
去括号得:,
移项合并同类项得:
系数化为1得:,
故选:A.
4.B
【分析】本题考查的是一元一次方程的解法,熟记去括号时,括号前面是符号,括号内各项都要改变符号是解本题的关键.
【详解】解:
去分母,得,第一步
去括号,得,第二步
∴出现错误在第二步,去括号时,括号前面的负号,去括号后,括号内第二项没有改变符号;
故选:B
5.C
【分析】本题考查了方程的解,将代入求解即可.
【详解】解:将代入,
得:,
解得:,
故选:C.
6.D
【分析】本题考查了一元一次方程的解和解含字母系数的一元一次方程,掌握方程的解即是正整数和是整数的两个条件是解题的关键.
首先求出关于的方程的解,解得,再根据方程的解为正整数,为整数,分类讨论即可求出的值.
【详解】解:由题可知,,
解得:,
方程的解为正整数,为整数,
或,
或,
故选:D.
7.A
【分析】本题主要考查了一元一次方程的应用,解题的关键是找出题目中的等量关系,根据空车日行七十里,重车日行五十里,五天往返三趟,列出方程即可.
【详解】解:设太仓到上林的距离为x里,往返一趟所用时间为天,根据题意得:
,
故选:A.
8.C
【分析】本题主要考查了解一元一次方程,根据“*”的定义,列方程并求解即可.
【详解】解:由题意可得
,
故选:C.
9.C
【分析】本题考查一元一次方程的应用,解答本题的关键是明确题意,求出x的值.先列方程求出x的值,再用大长方形的面积减去5个小长方形的面积即可.
【详解】解:由题意,得
,
∴,
∴,
故选:C.
10.A
【分析】本题考查了一元一次方程的应用,代数式求值,由题意可得到关于的两个一元一次方程,解方程即可求出的值,再把的值代入计算即可求解,根据题意,正确列出一元一次方程是解题的关键.
【详解】解:由题意可得,,,
解得,,
∴,
故选:.
11.
【分析】本题主要考查了等式的性质,根据式两边同时除以一个不为零的数字或式子等式仍然成立可得,即.
【详解】解:∵,
∴当成立时c应满足的条件是,即,
故答案为:.
12.(答案不唯一,只要合理即可)
【分析】根据方程解的定义,只要是把代入成立且满足相关条件即可.
【详解】解:方程可写为:(答案不唯一),
故答案为:(答案不唯一).
【点睛】本题考查了一元一次方程的解,理解方程的解是能使方程左右两边相等的未知数的值是解题的关键.
13.5
【分析】把方程的解代入方程即可得出的值.
【详解】把代入方程,得
∴
故答案为5.
【点睛】此题主要考查根据方程的解求参数的值,熟练掌握,即可解题.
14.
【分析】本题考查了一元一次方程的应用,读懂题意,根据题中的等量关系,列出方程是解题的关键.
设人剪筒身,则人剪筒底,根据一个筒身配两个筒底列出方程,解方程即可得到答案.
【详解】解:设人剪筒身,则人剪筒底,
根据题意得,,
解得:,
∴人剪筒身,才能使每小时剪出的筒身与筒底配套,
故答案为:.
15.或
【分析】本题考查两点间的距离公式,一元一次方程的实际应用.设表示的数为,根据,列出方程,求出的值,即可得出结果.正确的列出方程,是解题的关键.
【详解】解:设表示的数为,则:,
∵,
∴,
∴或,
∴D站台可称为或站台;
故答案为:或.
16.(1)
(2)
【分析】本题主要考查解一元一次方程,去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向形式转化.
依次去括号、移项、合并同类项、系数化为1可得;
依次去括号、移项、合并同类项、系数化为1可得.
【详解】(1)解:
移项得:
合并同类项得:
系数化为1,得:
(2)解:
去括号得:
移项得:
合并同类项得:
系数化为1,得:
17.(1);
(2)产生错误的原因:等式两边同时除以字母时,没有考虑字母是否为;的值为.
【分析】()根据等式的性质可知错误发生在第步;
()根据等式的基本性质即可解答;
本题考查了等式的基本性质,掌握等式的基本性质是解题的关键.
【详解】(1)解:第步等式变形产生错误,
故答案为:;
(2)解:产生错误的原因:等式两边同时除以字母时,没有考虑字母是否为.
正确过程:
两边同时加,得,
两边同时减,得,
两边同时除以,得.
18.A,B两地之间的距离为;
【分析】本题考查一元一次方程解决行程问题,根据两个的时间差列式求解即可得到答案;
【详解】解:设A,B两地之间的距离为,
由题意可得:
解得,
答:A,B两地之间的距离为.
19.(1),;
(2).
【分析】本题主要考查了解一元一次方程和一元一次方程的解,熟知方程的解是使方程左右两边相等的未知数的值是解题的关键.
(1)先求出方程的解,得到,再把这个解代入到方程中得到关于m的方程,据此求解即可;
(2)把,代入方程,解方程即可求解.
【详解】(1)解:
去括号得:,
移项得:,
合并得:,
把代入到方程中得:,
去括号得: ,
移项得:,
合并得:,
系数化为1得:;
(2)解:∵,,
∴关于的方程为,
整理得,
解得.
20.(1)七年级(1)班有男生人、女生人;
(2)男生共需要小时.
【分析】本题考查的是一元一次方程的应用,熟练的确定相等关系建立方程是解本题的关键.
(1)设七年级(1)班有男生有人,则女生有人,再利用全班共48人建立方程求解即可;
(2)设男生共需要小时,再由各部分的工作量之和等于1建立方程求解即可.
【详解】(1)解:设七年级(1)班有男生有人,则女生有人,
∴,
解得:;
∴,
答:七年级(1)班有男生人、女生人;
(2)设男生共需要小时,则
,
解得:;
答:男生共需要小时.
21.(1)甲单独加工完这批零件,需要15天,则甲单独加工完这批零件,需要10天.
(2)甲获得的报酬为元,乙获得的报酬为元.
【分析】本题考查的是一元一次方程的应用,理解题意,确定相等关系是解本题的关键;
(1)设甲单独加工完这批零件,需要天,则乙单独加工完这批零件,需要天,利用甲乙完成的工作量相等建立方程求解即可;
(2)设剩下的部分由甲、乙合做天,由各部分的工作量之和为1,建立方程求解工作时间,再计算工作报酬即可.
【详解】(1)解:设甲单独加工完这批零件,需要天,则乙单独加工完这批零件,需要天,则
,
解得:,
∴,
答:甲单独加工完这批零件,需要15天,甲单独加工完这批零件,需要10天,
(2)设剩下的部分由甲、乙合做天,则
,
解得:,
∴甲获得的报酬为(元),乙获得的报酬为(元).
22.(1)
(2)或
(3),
【分析】本题考查一元一次方程的知识,解题的关键是根据“和谐方程”的定义,一元一次方程的解,进行解答,即可.
(1)解出和的解,再根据“和谐方程”的定义,即可;
(2)根据“和谐方程”的定义,则一个方程的解为:;另一个方程的解为:,即可;
(3)先解出的解,再根据“和谐方程”的定义,即可.
【详解】(1)∵,
解得:,
∵,
∴,
∵方程与方程是“和谐方程”,
∴,
∴.
(2)∵“和谐方程”的两个解的差为,其中一个解为,
∴另一个方程的解为:,
∴,
解得:,
∴或.
(3)∵,
∴,
∴方程的解为:,
∴,
∴,
∴,
∵取任何有理数上式都成立,
∴,
\解得:,
∴,.
23.(1)260,612,800
(2)购买这种商品240件
(3)的值为1000
【分析】本题考查了一元一次方程的应用.
(1)根据不同的档,求出购买不同件数的花费;
(2)说先判断购买件数的范围,在根据所在档计算花费;
(3)根据:购买件商品的花费,列出关于n的方程,求解即可.
【详解】(1)解:买100件花:(元),
买300件花:(元),
买350件花:(元),
故答案为:260,700,800;
(2)解:设购买这种商品件,
因为花费,所以购买的件数少于300件,
解得:,
答:购买这种商品240件;
(3)解:当时,,
解得:(不符合题意,舍去),
当时,解得:,
综上所述:的值为1000
答案第1页,共2页
答案第1页,共2页
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.下列是一元一次方程的是( )
A. B. C. D.
2.已知,根据等式的基本性质,下列变形错误的是( )
A. B. C. D.
3.如果的值与的值相等,那么x的值为( )
A.9 B. C.3 D.
4.佳佳同学解一元一次方程的过程如下:
解:去分母,得,第一步
去括号,得,第二步
移项,得,第三步
合并同类项,得,第四步
系数化为1,得.
前四个步骤中,开始出现错误的是( )
A.第一步 B.第二步 C.第三步 D.第四步
5.小刚同学在做作业时,不小心将方程中的一个常数涂黑了,在询问老师后,老师告诉她方程的解是请问这个被涂黑的常数是( )
A. B.4 C. D.2
6.若关于x的方程的解为正整数,则整数k的值为( )
A.1 B.2 C.3或4 D.0或1
7.《九章算术》成书于公元1世纪,是古代中国乃至东方的第一部自成体系的数学专著,《九章算术》的算法体系至今仍在推动着计算机的发展和应用.书中记载了这样一题:“今有程传委输(驿站受托运粮),空车日行七十里,重车日行五十里.今载太仓粟输上林,五日三返(五天往返三趟).问太仓去(距离)上林几何(多远)?”用现在的解法,设太仓到上林的距离为x里,可列方程( )
A. B. C. D.
8.规定新运算“*”:对于任意实数都有,例如:,若,则的值为( )
A. B. C. D.1
9.已知一个小长方形的长和宽分别是和2,当5个形状、大小相同的小长方形拼成一个如图所示的大长方形,所标尺寸如图所示,求图中阴影部分面积是( )
A.18 B.27 C.29 D.33
10.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图),将个数填在的方格中,如果满足每行、每列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则的值为( )
A. B. C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如果,那么成立时c应满足的条件是 .
12.请你帮助乐乐同学写一个满足下列条件的一元一次方程:①含未知数项的系数为负数;②方程左边只有两项且右边等于零;③方程的解为.你写的方程是 .
13.已知关于的方程的解是,则的值为 .
14.在手工制作课上,老师组织七年级一班的学生用硬纸制作圆柱形茶叶筒.七年级一班共有学生人,每名学生每小时剪筒身个或剪筒底个.要求一个筒身配两个筒底,那么安排 人剪筒身,才能使每小时剪出的筒身与筒底配套.
15.电影《哈利·波特》中,哈利·波特穿墙进入“站台”的镜头(如图中的A站台),构思巧妙,给观众留下了深刻的印象.若B,C分别称为“站台”和“站台”,且,则D站台用类似电影中的方法可称为“ 站台”.
三、解答题
16.解方程:
(1);(2).
17.小明在学习了等式的基本性质后,对等式进行变形,得出“”的错误结论,但他找不到错误原因,聪明的你能帮助他找到原因吗?小明的具体过程如表所示:
将等式变形 两边同时加,得(第①步) 两边同时除以,得(第②步)
(1)第______步等式变形产生错误;
(2)请分析产生错误的原因,写出等式正确变形过程,求出的值.
18.如图是两张不同类型火车的车票:(“次”表示动车,“次”表示高铁).已知该动车和高铁的平均速度分别为,,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离.
19.已知关于的方程与有相同的解.
(1)求的值;
(2)求关于的方程的解.
20.在劳动课上,老师组织七年级(1)班的学生自己动手整理操场.七年级(1)班共有学生48人,其中女生人数比男生人数的多3人.如果让男生单独工作,需要5小时,如果让女生单独工作,需要小时.
(1)七年级(1)班有男生、女生各多少人?
(2)如果让男生、女生一起工作1小时,再由男生单独完成剩余的部分,求男生共需要多少时间?
21.某工厂要加工一批零件,请你根据甲、乙两位工人的对话内容(如图),解决下列问题.
(1)问甲、乙两位工人单独加工完这批零件,各需要多少天?
(2)这批零件,先由乙单独做5天,剩下的部分由甲、乙合做完成.那么加工完这批零件,甲、乙各获得多少报酬?
22.定义:如果两个一元一次方程的解互为相反数,我们就称这两个方程为“和谐方程”.
例如:方程和为“和谐方程”.
(1)若关于的方程与方程是“和谐方程”,求的值;
(2)若“和谐方程”的两个解的差为4,其中一个解为,求的值;
(3)若无论取任何有理数,关于的方程(,为常数)与关于的方程都是“和谐方程”,求与的值.
23.一种商品按销售量分三部分制定销售单价,如下表:
销售量 单价
不超过100件部分 2.6元/件
超过100件不超过300件部分 2.2元/件
超过300件部分 2元/件
(1)若买100件花______元,买260件花______元;买350件花______元;
(2)某社团为举行活动花了568元买这种商品作为纪念品,求购买这种商品多少件?
(3)若张强花了元,恰好购买件这种商品,求的值.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校
:___________
姓名:
___________
班级:
___________
考号:
___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.A
【分析】本题主要考查了一元一次方程的定义,一元一次方程的定义:只含有一个未知数,且未知数的次数是1,且两边都是整式,这样的方程叫一元一次方程.根据一元一次方程的定义一一判断即可.
【详解】解:A.只含有一个未知数,未知数的次数是1,且两边都是整式,是一元一次方程,故本选项符合题意;
B.分母中含有未知数,不是整式,不是一元一次方程,故本选项不符合题意;
A.只含有一个未知数,但不是等式,不是一元一次方程,故本选项不符合题意;
D.含有两个未知数,不是一元一次方程,故本选项不符合题意;
故选:A.
2.C
【分析】此题主要考查了等式的基本性质,等式的性质1、等式两边加同一个数(或式子)结果仍得等式;2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.根据等式的基本性质,对题目中的四个选项逐一进行判断即可得出答案.
【详解】解:将等式的两边同时加上1,得:,
故选项A正确,不符合题意;
将等式的两边同时减去1,得:,
故选项B正确,不符合题意;
将等式的两边同时乘以,得:,
故选项C不正确,符合题意;
将等式的两边同时除以2,得:,
故选项D正确,不符合题意.
故选:C.
3.A
【分析】此题考查了解一元一次方程,熟练掌握解法是解本题的关键.利用的值与的值相等,列出方程,求出方程的解即可得到x的值.
【详解】解:根据题意得:,
去括号得:,
移项合并同类项得:
系数化为1得:,
故选:A.
4.B
【分析】本题考查的是一元一次方程的解法,熟记去括号时,括号前面是符号,括号内各项都要改变符号是解本题的关键.
【详解】解:
去分母,得,第一步
去括号,得,第二步
∴出现错误在第二步,去括号时,括号前面的负号,去括号后,括号内第二项没有改变符号;
故选:B
5.C
【分析】本题考查了方程的解,将代入求解即可.
【详解】解:将代入,
得:,
解得:,
故选:C.
6.D
【分析】本题考查了一元一次方程的解和解含字母系数的一元一次方程,掌握方程的解即是正整数和是整数的两个条件是解题的关键.
首先求出关于的方程的解,解得,再根据方程的解为正整数,为整数,分类讨论即可求出的值.
【详解】解:由题可知,,
解得:,
方程的解为正整数,为整数,
或,
或,
故选:D.
7.A
【分析】本题主要考查了一元一次方程的应用,解题的关键是找出题目中的等量关系,根据空车日行七十里,重车日行五十里,五天往返三趟,列出方程即可.
【详解】解:设太仓到上林的距离为x里,往返一趟所用时间为天,根据题意得:
,
故选:A.
8.C
【分析】本题主要考查了解一元一次方程,根据“*”的定义,列方程并求解即可.
【详解】解:由题意可得
,
故选:C.
9.C
【分析】本题考查一元一次方程的应用,解答本题的关键是明确题意,求出x的值.先列方程求出x的值,再用大长方形的面积减去5个小长方形的面积即可.
【详解】解:由题意,得
,
∴,
∴,
故选:C.
10.A
【分析】本题考查了一元一次方程的应用,代数式求值,由题意可得到关于的两个一元一次方程,解方程即可求出的值,再把的值代入计算即可求解,根据题意,正确列出一元一次方程是解题的关键.
【详解】解:由题意可得,,,
解得,,
∴,
故选:.
11.
【分析】本题主要考查了等式的性质,根据式两边同时除以一个不为零的数字或式子等式仍然成立可得,即.
【详解】解:∵,
∴当成立时c应满足的条件是,即,
故答案为:.
12.(答案不唯一,只要合理即可)
【分析】根据方程解的定义,只要是把代入成立且满足相关条件即可.
【详解】解:方程可写为:(答案不唯一),
故答案为:(答案不唯一).
【点睛】本题考查了一元一次方程的解,理解方程的解是能使方程左右两边相等的未知数的值是解题的关键.
13.5
【分析】把方程的解代入方程即可得出的值.
【详解】把代入方程,得
∴
故答案为5.
【点睛】此题主要考查根据方程的解求参数的值,熟练掌握,即可解题.
14.
【分析】本题考查了一元一次方程的应用,读懂题意,根据题中的等量关系,列出方程是解题的关键.
设人剪筒身,则人剪筒底,根据一个筒身配两个筒底列出方程,解方程即可得到答案.
【详解】解:设人剪筒身,则人剪筒底,
根据题意得,,
解得:,
∴人剪筒身,才能使每小时剪出的筒身与筒底配套,
故答案为:.
15.或
【分析】本题考查两点间的距离公式,一元一次方程的实际应用.设表示的数为,根据,列出方程,求出的值,即可得出结果.正确的列出方程,是解题的关键.
【详解】解:设表示的数为,则:,
∵,
∴,
∴或,
∴D站台可称为或站台;
故答案为:或.
16.(1)
(2)
【分析】本题主要考查解一元一次方程,去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向形式转化.
依次去括号、移项、合并同类项、系数化为1可得;
依次去括号、移项、合并同类项、系数化为1可得.
【详解】(1)解:
移项得:
合并同类项得:
系数化为1,得:
(2)解:
去括号得:
移项得:
合并同类项得:
系数化为1,得:
17.(1);
(2)产生错误的原因:等式两边同时除以字母时,没有考虑字母是否为;的值为.
【分析】()根据等式的性质可知错误发生在第步;
()根据等式的基本性质即可解答;
本题考查了等式的基本性质,掌握等式的基本性质是解题的关键.
【详解】(1)解:第步等式变形产生错误,
故答案为:;
(2)解:产生错误的原因:等式两边同时除以字母时,没有考虑字母是否为.
正确过程:
两边同时加,得,
两边同时减,得,
两边同时除以,得.
18.A,B两地之间的距离为;
【分析】本题考查一元一次方程解决行程问题,根据两个的时间差列式求解即可得到答案;
【详解】解:设A,B两地之间的距离为,
由题意可得:
解得,
答:A,B两地之间的距离为.
19.(1),;
(2).
【分析】本题主要考查了解一元一次方程和一元一次方程的解,熟知方程的解是使方程左右两边相等的未知数的值是解题的关键.
(1)先求出方程的解,得到,再把这个解代入到方程中得到关于m的方程,据此求解即可;
(2)把,代入方程,解方程即可求解.
【详解】(1)解:
去括号得:,
移项得:,
合并得:,
把代入到方程中得:,
去括号得: ,
移项得:,
合并得:,
系数化为1得:;
(2)解:∵,,
∴关于的方程为,
整理得,
解得.
20.(1)七年级(1)班有男生人、女生人;
(2)男生共需要小时.
【分析】本题考查的是一元一次方程的应用,熟练的确定相等关系建立方程是解本题的关键.
(1)设七年级(1)班有男生有人,则女生有人,再利用全班共48人建立方程求解即可;
(2)设男生共需要小时,再由各部分的工作量之和等于1建立方程求解即可.
【详解】(1)解:设七年级(1)班有男生有人,则女生有人,
∴,
解得:;
∴,
答:七年级(1)班有男生人、女生人;
(2)设男生共需要小时,则
,
解得:;
答:男生共需要小时.
21.(1)甲单独加工完这批零件,需要15天,则甲单独加工完这批零件,需要10天.
(2)甲获得的报酬为元,乙获得的报酬为元.
【分析】本题考查的是一元一次方程的应用,理解题意,确定相等关系是解本题的关键;
(1)设甲单独加工完这批零件,需要天,则乙单独加工完这批零件,需要天,利用甲乙完成的工作量相等建立方程求解即可;
(2)设剩下的部分由甲、乙合做天,由各部分的工作量之和为1,建立方程求解工作时间,再计算工作报酬即可.
【详解】(1)解:设甲单独加工完这批零件,需要天,则乙单独加工完这批零件,需要天,则
,
解得:,
∴,
答:甲单独加工完这批零件,需要15天,甲单独加工完这批零件,需要10天,
(2)设剩下的部分由甲、乙合做天,则
,
解得:,
∴甲获得的报酬为(元),乙获得的报酬为(元).
22.(1)
(2)或
(3),
【分析】本题考查一元一次方程的知识,解题的关键是根据“和谐方程”的定义,一元一次方程的解,进行解答,即可.
(1)解出和的解,再根据“和谐方程”的定义,即可;
(2)根据“和谐方程”的定义,则一个方程的解为:;另一个方程的解为:,即可;
(3)先解出的解,再根据“和谐方程”的定义,即可.
【详解】(1)∵,
解得:,
∵,
∴,
∵方程与方程是“和谐方程”,
∴,
∴.
(2)∵“和谐方程”的两个解的差为,其中一个解为,
∴另一个方程的解为:,
∴,
解得:,
∴或.
(3)∵,
∴,
∴方程的解为:,
∴,
∴,
∴,
∵取任何有理数上式都成立,
∴,
\解得:,
∴,.
23.(1)260,612,800
(2)购买这种商品240件
(3)的值为1000
【分析】本题考查了一元一次方程的应用.
(1)根据不同的档,求出购买不同件数的花费;
(2)说先判断购买件数的范围,在根据所在档计算花费;
(3)根据:购买件商品的花费,列出关于n的方程,求解即可.
【详解】(1)解:买100件花:(元),
买300件花:(元),
买350件花:(元),
故答案为:260,700,800;
(2)解:设购买这种商品件,
因为花费,所以购买的件数少于300件,
解得:,
答:购买这种商品240件;
(3)解:当时,,
解得:(不符合题意,舍去),
当时,解得:,
综上所述:的值为1000
答案第1页,共2页
答案第1页,共2页
